スペクトル解析の基礎と可視化

スペクトル解析の基礎と可視化#

前項、周波数解析の基礎ではフーリエ級数・フーリエ変換・離散時間フーリエ変換・離散フーリエ変換の4種類の変換について解説し、信号の時間領域の表現（時刻の関数としての表現）を周波数領域での表現へと変換する方法を見てきました。その小括でも述べた通り、これら4種類の変換はいずれも元の信号の全体にわたって行われるもので、音声信号や複雑な時系列データのように時刻によって周波数成分の変化する信号の表現には十分でありません。本項ではこういった周波数成分の時間変化を捉えて表現するための方法として短時間フーリエ変換とその離散化を解説した上で、これら各種のフーリエ変換を応用して周波数領域での信号の解析を行うスペクトル解析についての初歩的な内容を確認していきます。

import matplotlib.pyplot as plt
import numpy as np

短時間フーリエ変換とその離散化#

観測された信号の周波数領域における表現を抽出する変換のうち、別稿でも解説した基本的な

  • フーリエ級数展開

  • フーリエ変換 (Fourier transform; FT)

  • 離散時間フーリエ変換 (discrete-time Fourier transform; DTFT)

  • 離散フーリエ変換 (discrete Fourier transform; DFT)

の4種類は、対象となる信号が時間領域で周期的か否か、連続的か否かの違いこそあれ、いずれも観測された信号の全時刻にわたって適用されるものでした（フーリエ変換と離散フーリエ変換は周期信号の一周期分を考えています）。それゆえこれらの変換には応用上の共通した課題があり、例えば

  • 音声信号のように時刻によって周波数成分が変化する場合、その変化を抽出できない、あるいは

  • 一般の時系列データのように、必ずしも周期的でないランダムな信号では（原理的に）変換が実行できない

といった点が挙げられます。 短時間フーリエ変換 (short-time Fourier tranform; STFT) はこれらの課題に対応するもので、元の信号に 窓関数 (window function) と呼ばれる関数を掛け合わせた信号に対してフーリエ変換を行います。

連続時間の信号に対する短時間フーリエ変換#

元の信号が時刻の関数 \(x ( t )\) として表現されているものとします。このとき窓関数 \(w ( t )\) として \(t = 0\) の近傍以外で消える（値が0になる）ものを選んで

\[ X ( \tau, \omega ) = \int_{- \infty}^\infty x ( t ) w ( t - \tau ) e^{- i \omega t} d t \]

としたとき、この \(x ( t )\) から \(X ( \tau, \omega )\) への変換を短時間フーリエ変換と呼びます。例えば窓関数 \(w ( t )\) が区間 \([- T / 2, T / 2)\) 以外で消えるとすると、上記の変換は

\[ X ( \tau, \omega ) = \int_{- \frac{T}{2}}^\frac{T}{2} x ( t ) w ( t - \tau ) e^{- i \omega t} d t \]

と書くことができます。これは関数 \(x ( t ) w ( t - \tau )\) を \(\tau - T / 2 \le t < \tau + T / 2\) の範囲だけ切り取って基本周期 \(T\) の周期関数と見なした上で、通常のフーリエ級数展開に相当する変換を行っていることに相当します。窓関数 \(w ( t )\) として選択される関数は多くが \(t = 0\) を頂点とした山なりの形状をしているため、短時間フーリエ変換はしばしば時刻 \(\tau\) の周辺に限定した \(x ( t )\) の局所的な周波数表現を与えるものとして解釈されます。

短時間フーリエ変換の逆変換として 逆短時間フーリエ変換 (inverse short-time Fourier transform; ISTFT) を考えることができ、上記のように求めた \(X (t, \omega )\) に対して

\[ x ( t ) w ( t - \tau ) = \frac{1}{2 \pi} \int_{- \infty}^\infty X ( \tau, \omega ) e^{i \omega t} d \omega \]

および

\[ x ( t ) = \frac{1}{W} \int_{- \infty}^\infty \left( \frac{1}{2 \pi} \int_{- \infty}^\infty X ( \tau, \omega ) e^{i \omega t} d \omega \right) d \tau \]

が成り立ちます。ただし \(W = \int_{- \infty}^\infty w ( \tau ) d \tau\) とおきました。

窓関数の選択#

短時間フーリエ変換で利用される窓関数 \(w ( t )\) のうち、代表的なものをいくつか解説します。

短時間フーリエ変換では窓関数をかけて元の信号 \(x ( t )\) を歪めている以上、変換で得られる周波数特性も元の信号の特性とは微妙に異なったものになります。この際、元の信号の周波数成分について

  • 複数のピークがあった場合、どれほど離れていれば識別できるか（周波数分解能が高いか）、および

  • 本来のピークを雑音からどれほど識別できるか（ダイナミックレンジが広いか）

の間にはトレードオフの関係があり、利用する窓関数によってそのバランスが異なります。このため、短時間フーリエ変換で利用する窓関数は解析の目的や対象の信号の性質に応じて適切に選択する必要があります。以下では代表的な窓関数を3つ紹介しますが、これ以外にも多数の窓関数が考案され、利用されています。

SciPyにおいては scipy.signal.windows モジュールに代表的な窓関数が格納されています。

矩形窓#

矩形窓 (rectangular window) は

\[\begin{split} w ( t ) = \begin{cases} 1 , & - \frac{T}{2} \le t < \frac{T}{2} \\ 0 , & \text{otherwise} \end{cases} \end{split}\]

として表される窓関数で、単に \(x ( t )\) を \(\tau - T / 2 \le t < \tau + T / 2 \) の範囲だけ切り取ってフーリエ変換をしている場合はこの窓を利用していることになります。一般の \(x ( t )\) では \(x ( t ) w ( t - \tau )\) が \(t = \tau - T / 2\) と \(t \nearrow \tau + T / 2\) で異なる値を取ることから、短時間フーリエ変換において矩形窓を利用する場合は周期の境界で不連続な周期関数のフーリエ級数展開を考えていることになります。

矩形窓は周波数分解能こそ極めて高いもののダイナミックレンジが余りに狭く、実用上はあまり用いられません。

t = np.arange(-5, 5, 0.1)  # -5 <= t < 5 の範囲で0.1刻みでサンプリング (100時刻分)
x = np.sin(t) - np.cos(2 * t)  # 元の信号；2つの周期成分を持つ関数

from scipy.signal.windows import boxcar  # 矩形窓

_w = boxcar(41)  # T=4 として -2<=tau<=2 の41時刻分の窓関数
w = np.zeros_like(x)  # 仮に0埋め
w[30 : (30 + _w.shape[0] - 1)] = _w[:(-1)]  # t=0 を中心にした窓関数の値 (t=2 を除く)

fig, ax = plt.subplots(figsize=(10, 5))

ax.plot(t, x, label="original sig.", c="C0")  # 元の信号（青色）
ax.plot(t, w, label="window", c="C1")  # 窓関数（橙色）
ax.plot(t, w * x, label="windowed sig.", c="C2")  # 元の信号と窓関数との積（緑色）
ax.grid()
ax.legend()
ax.set_title("Deformation with a Rectangular Window")
ax.set_xlabel("t")
ax.set_ylabel("x")

Text(0, 0.5, 'x')
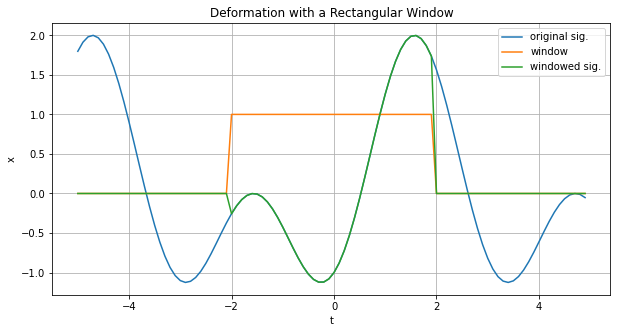
../_images/d5858588f31412569d35ed6aab5719dcc815e26e54a32caee0a6f0117bfdef53.png

上図の青線が元の信号、橙線が窓関数、緑線が窓関数をかけた信号を表しています。元の信号は周期的でしたが、矩形窓の長さが周期長と一致しないために窓関数をかけた信号は両端の値が一致していないことに注意してください。このことがダイナミックレンジの狭さに繋がっています。

ハン窓#

ハン窓 (Hann window) は

\[\begin{split} w ( t ) = \begin{cases} 0.5 + 0.5 \cos \frac{2 \pi t}{T} , & - \frac{T}{2} \le t < \frac{T}{2} \\ 0 , & \text{otherwise} \end{cases} \end{split}\]

として表される窓関数で、周期 \(T\) の余弦関数を値が \([0, 1]\) の範囲に収まるようにスケールしたものになっています。 \(w ( t - \tau )\) の値が \(t = \tau - T / 2\) と \(t \nearrow \tau + T / 2\) で消えるため、 \(x ( t ) w ( t - \tau )\) を周期の両端で連続な周期関数として考えることができます。短時間フーリエ変換では最もよく用いられる窓関数の一つです。

ハン窓は全体的にダイナミックレンジが広いものの、周波数分解能はそこまで高くないため周波数の近い複数の信号があるとうまく識別できない可能性があります。

from scipy.signal.windows import hann  # ハン窓

_w = hann(41)  # T=4 として -2<=tau<2 の41時刻分の窓関数
w = np.zeros_like(x)  # 仮に0埋め
w[30 : (30 + _w.shape[0] - 1)] = _w[:(-1)]  # t=0 を中心にした窓関数の値 (t=2 を除く)

fig, ax = plt.subplots(figsize=(10, 5))

ax.plot(t, x, label="original sig.", c="C0")  # 元の信号（青色）
ax.plot(t, w, label="window", c="C1")  # 窓関数（橙色）
ax.plot(t, w * x, label="windowed sig.", c="C2")  # 元の信号と窓関数との積（緑色）
ax.grid()
ax.legend()
ax.set_title("Deformation with a Hann Window")
ax.set_xlabel("t")
ax.set_ylabel("x")

Text(0, 0.5, 'x')
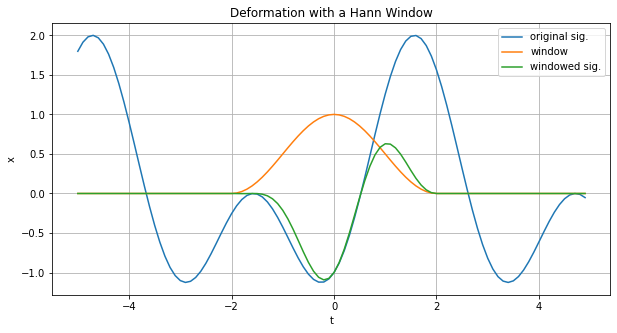
../_images/4948cc7e967faf78d66d261f4653124539d51424a6179d55ba36ac3ab7621b14.png

上図でもハン窓の長さは元の信号の周期長と一致していませんが、ハン窓は両端で0に消えるため確かに窓関数をかけた信号は両端の値が0で一致しています。一方で、特に窓内の右側で顕著ですが窓をかけた波形が窓の中央に向かって歪められることになり、矩形窓と比べた周波数分解能の悪さもこれに起因しています。

ハミング窓#

ハミング窓 (Hamming window) は

\[\begin{split} w ( t ) = \begin{cases} 0.54 + 0.46 \cos \frac{2 \pi t}{T} , & - \frac{T}{2} \le t < \frac{T}{2} \\ 0 , & \text{otherwise} \end{cases} \end{split}\]

として表される窓関数で、ハン窓の係数を調整して改良したものになっています。 \(w ( t - \tau )\) の値が \(t = \tau - T / 2\) と \(t \nearrow \tau + T / 2\) で消えずに \(0.08\) だけ残るため、矩形窓ほど極端ではありませんがやはり周期の両端で不連続な周期関数を考えていることになります。こちらもハン窓と並んで最もよく用いられる窓関数の一つです。

ハミング窓はハン窓と比べて周波数分解能が高く、複数の信号で周波数がある程度近くても互いに識別することができます。一方でダイナミックレンジはハン窓ほど広くなく、弱い信号に対応するピークを取りこぼしてしまう場合もあります。

from scipy.signal.windows import hamming  # ハミング窓

_w = hamming(41)  # T=4 として -2<=tau<=2 の41時刻分の窓関数
w = np.zeros_like(x)  # 仮に0埋め
w[30 : (30 + _w.shape[0] - 1)] = _w[:(-1)]  # t=0 を中心にした窓関数の値 (t=2 を除く)

fig, ax = plt.subplots(figsize=(10, 5))

ax.plot(t, x, label="original sig.", c="C0")  # 元の信号（青色）
ax.plot(t, w, label="window", c="C1")  # 窓関数（橙色）
ax.plot(t, w * x, label="windowed sig.", c="C2")  # 元の信号と窓関数との積（緑色）
ax.grid()
ax.legend()
ax.set_title("Deformation with a Hamming Window")
ax.set_xlabel("t")
ax.set_ylabel("x")

Text(0, 0.5, 'x')
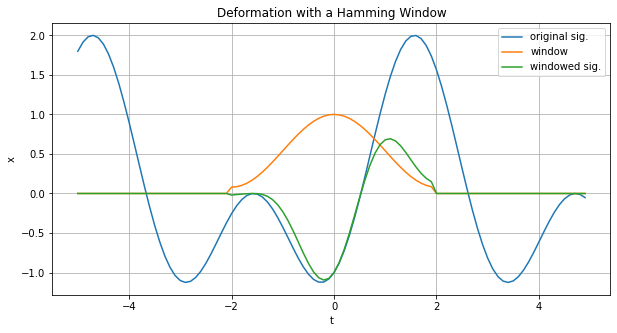
../_images/df950c9aec9835b6bba10d8e52d1a7953e5538b405f052814260a8ff5aff24cd.png

上図をハン窓の場合と比べると、窓関数が両端で完全には消えていないため窓をかけた信号も両端で（矩形窓ほど極端ではないにせよ）値が一致せず、一方で波形の歪みは僅かながら小さくなっています。

離散時間の信号に対する短時間フーリエ変換#

標本化周期 \(\Delta t\) の離散時間信号 \(x_n = x ( n \Delta t )\) に対しても同様の変換を定義することができます。窓関数 \(w ( t )\) は \(w_n = w ( n \Delta t - t_0 )\) が \(n = 0, 1, \ldots, N - 1\) においてのみ値を持つように一次変換されているとします（例えば元の窓関数 \(w ( t )\) が \([ - T/2, T/2 )\) 以外で消える場合、代わりに \(w ( T t / N - T/2 )\) を考えて記号を流用します）。このとき

\[ X_{n'} ( \omega ) = \sum_{n = 0}^{N - 1} x_{n + n'} w_n e^{- i \omega n} \]

は離散時間信号の一部 \(( x_{n'}, x_{n' + 1}, \ldots, x_{n' + N - 1} )\) （ フレーム (frame) とも）に窓関数をかけて離散時間フーリエ変換したものになっており、これも用語を流用して短時間フーリエ変換 (STFT) と呼びます。これ以外の \(n\) で \(x_{n + n'} w_n\) は消えるため、これを周期信号と思って

\[ X_{n', k} = \sum_{n = 0}^{N - 1} x_{n + n'} w_n e^{- i \frac{2 \pi k}{N} n} \]

を離散フーリエ変換（というより高速フーリエ変換）で求めることもよく行われ、やはりこれも用語を流用して短時間フーリエ変換と呼びます。実用上は、さらにフレームの開始時刻を \(n' = m H\) のように一定の間隔 \(H\) ごとに定めてこの \(m\) を添字とした

\[ X_{m, k} = \sum_{n = 0}^{N - 1} x_{n + m H} w_n e^{- i \frac{2 \pi k}{N} n} \]

の形で用いられることもあります。

逆変換については、単純に \(X_{m, k}\) に逆離散フーリエ変換を施した

\[ \tilde{x}_{m, n} = \frac{1}{N} \sum_{k = 0}^{N - 1} X_{m, k} e^{i \frac{2 \pi k}{N} n} \]

が \(n = 0, 1, \ldots, N - 1\) については \(x_{n + m H} w_n\) をよく復元していると考えられるので、これを \(m\) について（即ち、複数のフレームについて）適当に加重平均して元の \(x_n\) を復元することを考えます。よく行われるのはオーバーラップ加算 (overlap-add; OLA) という再構成方法で、

\[ \hat{x}_n = \frac{\sum_{m = -\infty}^{\infty} w_{n - m H} \tilde{x}_{m, n - m H}}{\sum_{m = -\infty}^{\infty} w_{n - m H}^2} \]

のように加重平均したもので \(x_n\) を復元します。式中の \(w_{n - m H}\) は元の \(x_n\) が含まれる \(N / H\) 個のフレーム以外では消えるため、分子・分母の総和はいずれも有限和になることに注意してください。この逆変換についても用語を流用して逆短時間フーリエ変換 (ISTFT) と呼びます。

離散時間信号に対するSTFTとISTFTは scipy.signal の stft と istft でそれぞれ実装されており、簡単に利用することができます。

例（周波数成分が変化する関数のSTFT）#

次の連続時間信号

\[ x ( t ) = \frac{\exp (- \beta t)}{1 + \exp (- \beta t)} \sin (2 \pi f_0 t) + \frac{1}{1 + \exp (- \beta t)} \sin (2 \pi f_1 t) \]

が \(-10 \le t < 10\) において標本化周波数 \(f_s = 100\) で標本化されているものとし、この離散時間信号のSTFTを考えます。関数 \(x ( t )\) は2つの異なる周波数成分 \(f_0 = 15\) と \(f_1 = 10\) の信号を時間変化する比率（ \(\beta = 0.4\) で定まるロジスティック関数）で混合したものになっていて、 \(t\) が小さいほど周波数 \(f_0\) の成分が、 \(t\) が大きいほど周波数 \(f_1\) の成分が支配的になるようになっています。

from scipy.constants import pi
from scipy.signal import stft, istft
from scipy.special import expit

beta = 0.4
f0 = 15.0
f1 = 10.0

tt = np.arange(
    -10.0, 10.0, 0.01
)  # -10 <= t < 10 の範囲で0.01刻みでサンプリング (2000時刻分)
xx = (1.0 - expit(beta * tt)) * np.sin(2.0 * pi * f0 * tt) + expit(beta * tt) * np.cos(
    2.0 * pi * f1 * tt
)  # 元の信号

離散時間信号 xx を関数 stft で短時間フーリエ変換すると次のようになります。

f, t, Zxx = stft(  # STFTを行う関数
    xx,  # 離散時間信号；デフォルトではFFT等の必要に応じて末尾にzero-paddingされる
    fs=100.0,  # 標本化周波数
    # window='hann',  # 窓関数の種類；デフォルトではハン窓
    # nperseg=256,  # Nの値；デフォルトでは256
    # noverlap=None,  # Hの値；デフォルトではN/2
)

関数 stft の返り値は3つ組のタプルになっており、順に

  • f: STFTで検出される周波数の第 \(k\) 成分の値を格納したNumPy配列

  • t: STFTで用いる第 \(m\) フレームの中心となる時刻を格納したNumPy配列

  • Zxx: STFTした \(X_{m, k}\) の値で、 (f.shape[0], t.shape[0])-shapedの複素数値NumPy配列

となっています。これを利用してスペクトログラム（各周波数成分の大きさを可視化したもの；詳細は後述）をプロットすることが可能です。ここでは単に Zxx の絶対値をプロットしてみます。

plt.pcolormesh(t - 10.0, f, np.abs(Zxx), vmin=0.0, vmax=1.0, shading="gouraud")
plt.title("STFT Magnitude")
plt.ylabel("Frequency [Hz]")
plt.xlabel("Time [sec]")
plt.show()
../_images/e505a2c511b02c3dec0709abc69e6c1fe19c8d1cf7f7bebb50158a1ea049291a.png

返り値 t はSTFTへの入力配列 xx の第0成分が時刻0に対応するものとして計算されているので、今回の場合は t - 10. が元の時刻 \(t\) に対応します。時刻 \(t = 0\) より前では \(f_0 = 15\) 付近で、それ以降は \(f_1 = 10\) 付近の周波数が支配的になっており、確かに元の信号の傾向と一致しています。

さて、この Zxx を関数 istft で逆短時間フーリエ変換すると次のようになります。

t_rec, x_rec = istft(  # ISTFTを行う関数
    Zxx,  # STFTの結果
    fs=100.0,  # 標本化周波数
    # window='hann',  # 窓関数の種類；デフォルトではハン窓
    # nperseg=None,  # Nの値；デフォルトでは `2 * (Zxx.shape[-2] - 1)`
    # noverlap=None,  # Hの値；デフォルトでは N/2
)

関数 istft の返り値は2つ組のタプルになっており、順に

  • t (今回は記号の重複を避けるために t_rec に格納): ISTFTの結果の第 \(n\) 成分に対応する時刻の値

  • x (今回は記号の重複を避けるために x_rec に格納): ISTFTした \(\hat{x}_n\) の値で、 (t.shape[0],)-shapedのNumPy配列

となっています。これが元の信号とどれほど一致しているか確認してみましょう。

tt.shape

(2000,)

n_padding = (
    x_rec.shape[0] - xx.shape[0]
)  # STFTに先立って元の信号の末尾にzero-paddingされた長さの組
t_rec_ = (
    t_rec[:(-n_padding)] - 10.0
)  # 再構成した信号の時刻から元の信号の時刻に対応する部分を切り出したもの
x_rec_ = x_rec[
    :(-n_padding)
]  # 再構成した信号から元の信号に対応する部分を切り出したもの

fig, ax = plt.subplots(figsize=(10, 5))

ax.plot(tt, xx, label="original sig.", c="C0")  # 元の信号（青色）
ax.plot(
    t_rec_, x_rec_, label="reconstructed sig.", c="C1"
)  # STFTとISTFTで再構成した信号（橙色）
ax.grid()
ax.legend()
ax.set_title("Reconstruction via STFT and ISTFT")
ax.set_xlabel("t")
ax.set_ylabel("x")

Text(0, 0.5, 'x')
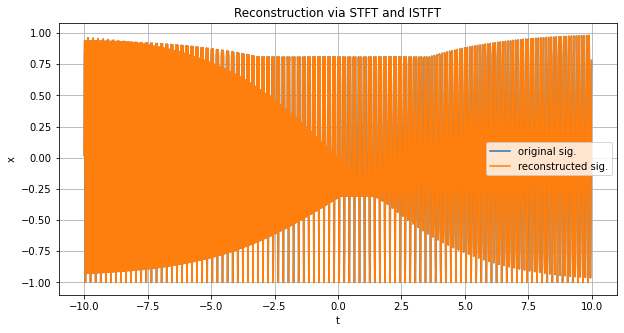
../_images/c8c97a17bc63349296c27b8ec7f638fb8d5e40550e32747dc499700e5e25ff38.png

上図の青色の線が元の離散時間信号、橙色の線がSTFTとISTFTによって再構成した離散時間信号になります。両者はほとんど重なっており、うまく元の信号が復元できていることが確認できます。念のため二乗誤差の平均も計算しておきましょう。

((xx - x_rec_) ** 2).mean()

1.941325650157724e-32

スペクトル解析の基礎#

所与の連続時間信号 \(x ( t )\) または離散時間信号 \(x_n\) の性質を解析する際、元の時間領域での表現のまま解析するのでなく、各種のフーリエ変換を通じて周波数領域での表現に変換してから解析することを スペクトル解析 (spectral analysis) と呼びます。周波数領域の表現を得るには各種のフーリエ変換を行えばよいのですが、時系列解析やDCSデータの解析で現れる信号の多くはランダムな雑音を含むものであり、厳密には通常の意味でのフーリエ変換を行うことができません。以下では初めに定常信号のスペクトル解析の基礎を解説し、続いて時変信号のスペクトル解析の手法を説明します。

パワースペクトル密度#

ランダムな連続時間信号 \(x ( t )\) が定常であると仮定します。このとき \(x ( t )\) の両端を切断した信号

\[\begin{split} x_T ( t ) = \begin{cases} x ( t ), & | t | \le \frac{T}{2} \\ 0, & | t | > \frac{T}{2} \end{cases} \end{split}\]

を考えると、この信号は雑音が両端で消えるのでフーリエ変換できて、

\[ X_T ( \omega ) = \int_{- \infty}^\infty x_T ( t ) e^{- i \omega t} dt = \int_{- \frac{T}{2}}^\frac{T}{2} x ( t ) e^{- i \omega t} dt \]

とおくことにします。さらに、一定の条件下で

\[ \lim_{T \to \infty} \frac{1}{T} \int_{- \frac{T}{2}}^\frac{T}{2} {x ( t )}^2 d t = \frac{1}{2 \pi} \int_{- \infty}^\infty \lim_{T \to \infty} \frac{| X_T ( \omega ) |^2}{T} d \omega \]

となるので、右辺の被積分項

\[ S_x ( \omega ) = \lim_{T \to \infty} \frac{| X_T ( \omega ) |^2}{T} \]

はこの信号のパワーを周波数領域に分解して表現したものと考えられます。この \(S_x ( \omega )\) を パワースペクトル密度 (power spectral density; PSD) と呼びます。

パワースペクトル密度はランダムな信号の自己相関関数

\[ \phi_x ( \tau ) = \lim_{T \to \infty} \frac{1}{T} \int_{- \frac{T}{2}}^\frac{T}{2} x_T ( t ) x_T ( t + \tau ) d t \]

とフーリエ変換対の関係にあります。即ち

\[\begin{split} S_x ( \omega ) = \int_{- \infty}^\infty \phi_x ( \tau ) e^{- i \omega \tau} d \tau, \\ \phi_x ( \tau ) = \frac{1}{2 \pi} \int_{- \infty}^\infty S_x ( \omega ) e^{i \omega \tau} d \omega \end{split}\]

の関係が成り立っており、これを ウィーナー・ヒンチンの定理 (Wiener-Khinchin theorem) と呼びます。

以上は連続時間信号の例でしたが、離散時間信号 \(x_n\) についても同様の議論が成り立ちます。

ピリオドグラムによるPSDの推定#

離散時間信号における最も基本的なPSDの推定方法は ピリオドグラム (periodogram) を用いることです。即ち、形式的に（潜在的にはランダムな）信号の離散フーリエ変換 \(x_n \mapsto X_k\) を行った上で

\[ \hat{S}_{x, k} = \frac{1}{N} | X_k |^2 \]

として、これをPSDの推定値とします。

ピリオドグラムによるPSDの推定は scipy.signal.periodogram に実装されています。

Welchの方法によるPSDの推定#

ピリオドグラムによるPSDの推定は、用いる（定常）時系列を長くしても誤差が小さくならないという欠点があります。このため

  1. 時系列を重なり合う複数のセグメントに分割し、窓関数をかけてからDFTをした修正ピリオドグラム (modified periodogram) を求める

  2. 各セグメントの修正ピリオドグラムを平均してPSDの推定値とする

とする方法がよく用いられ、これを ウェルチの方法 (Welch's method) と呼びます。これは元の信号に対して通常のSTFTを行った後、結果を二乗して周波数毎に平均していることに相当します。

Welchの方法によるPSDの推定は scipy.signal.welch に実装されています。

例（ピリオドグラムとWelchの方法によるPSDの推定）#

2つの周期成分を持つ関数

\[ x ( t ) = \sin ( 2 \pi \cdot 7 t ) - \cos ( 2 \pi \cdot 13 t ) \]

を \(- 5 \le t < 5\) の範囲で標本化周波数 \(f_s = 100\) として標本化し、この離散時間信号のPSDを求めます。

from scipy.signal import periodogram, welch

np.random.seed(42)

t = np.arange(-5, 5, 0.01)  # -5 <= t < 5 の範囲で0.01刻みでサンプリング (1000時刻分)
x = np.sin(2.0 * pi * 7.0 * t) - np.cos(
    2.0 * pi * 13.0 * t
)  # 元の信号；2つの周期成分を持つ関数
x_ = x + np.random.normal(scale=1.0, size=x.shape)

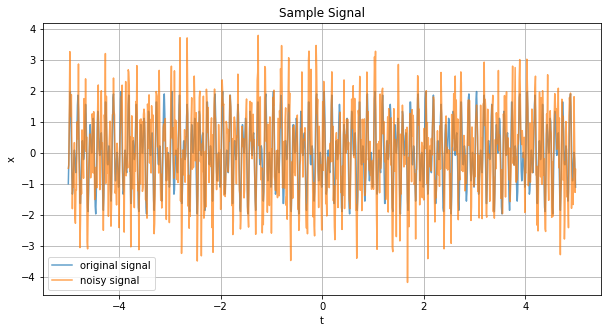
fig, ax = plt.subplots(figsize=(10, 5))

ax.plot(t, x, label="original signal", c="C0", alpha=0.7)
ax.plot(t, x_, label="noisy signal", c="C1", alpha=0.7)
ax.set_title("Sample Signal")
ax.set_xlabel("t")
ax.set_ylabel("x")
ax.grid()
ax.legend()

<matplotlib.legend.Legend at 0x13975fb50>
../_images/01cbb552bcc16f14a3630c1dc7f260d8bcdfc4a18512c2f22cfb7cf59d073763.png 
ff_per, s_per = periodogram(  # ピリオドグラムによるPSDの推定を行う関数
    x_,  # 信号
    fs=100.0,  # 標本化周波数
    # window='boxcar',  # 窓関数。矩形窓以外を用いる場合、修正ピリオドグラムと呼ぶ。
    # scaling='density',  # 返り値の指定。デフォルトではPSD。 'spectrum' にするとパワースペクトル。
)
ff_welch, s_welch = welch(  # Welchの方法によるPSDの推定を行う関数
    x_,  # 信号
    fs=100.0,  # 標本化周波数
    # window='hann',  # 窓関数。デフォルトではハン窓。
    nperseg=128,  # セグメントの長さ。
    # noverlap=None,  # セグメントの重なりの長さ。デフォルトではnpersegの半分。
    # scaling='density',  # 返り値の指定。デフォルトではPSD。 'spectrum' にするとパワースペクトル。
)

fig, ax = plt.subplots(figsize=(10, 5))

ax.plot(ff_per, s_per, label="PSD by periodogram", c="C0")
ax.plot(ff_welch, s_welch, label="PSD by Welch's method", c="C1")
ax.set_title("Estimation of PSD")
ax.set_xlabel("frequency")
ax.set_ylabel("PSD")
ax.grid()
ax.legend()

<matplotlib.legend.Legend at 0x1397ef750>
../_images/db7cfba18c9f57652e06f76b4e8c57f53e1f27c65798c72c0281fdd9b0f0e99a.png

ピリオドグラムによる推定（上図の青線）では入力系列の全体をDFTにかけているので、より短いセグメントをDFTにかけているWelchの方法による推定（上図の橙線）より周波数の分解能が細かくなっています。ピーク自体はピリオドグラムによる推定の方が鋭くなっていますが、雑音に対応する成分はWelchの方法の方がよく消えています。

クロススペクトル密度#

2つのランダムな信号 \(x ( t )\) および \(y ( t )\) に対して、PSDの場合と同様に \(x_T, X_T, y_T, Y_T\) を定義して、

\[ S_{xy} ( \omega ) = \lim_{T \to \infty} \frac{X_T^* ( \omega ) Y_T ( \omega )}{T} \]

を クロススペクトル密度 (cross spectral desity; CSD) または クロスパワースペクトル密度 (cross power spectral density; CPSD) と呼びます。ただし \(X_T^*\) は \(X_T\) の複素共役です。定義より明らかに

\[ S_{yx} ( \omega ) = S_{xy} ( - \omega ) \]

となります。また、簡単な計算により

\[ | S_{xy} ( \omega ) |^2 \le |S_{x} ( \omega )| |S_{y} ( \omega )| \]

であることも分かるため、クロススペクトル密度を正規化した

\[ \gamma^2_{xy} = \frac{| S_{xy} ( \omega ) |^2}{S_{x} ( \omega ) S_{y} ( \omega )} \]

という関数を考えることができ、これを コヒーレンス (coherence) と呼びます。

やはりPSDの場合と同様に、クロススペクトル密度はランダムな信号の相互相関関数

\[ \phi_{xy} ( \tau ) = \lim_{T \to \infty} \frac{1}{T} \int_{- \frac{T}{2}}^\frac{T}{2} x_T ( t ) y_T ( t + \tau ) d t \]

とフーリエ変換対の関係にあります。即ち

\[\begin{split} S_{xy} ( \omega ) = \int_{- \infty}^\infty \phi_{xy} ( \tau ) e^{- i \omega \tau} d \tau, \\ \phi_{xy} ( \tau ) = \frac{1}{2 \pi} \int_{- \infty}^\infty S_{xy} ( \omega ) e^{i \omega \tau} d \omega \end{split}\]

の関係が成り立っています。

クロススペクトル密度の推定#

離散時間信号におけるCSDの推定も、やはり形式的に信号の離散フーリエ変換 \(x_n \mapsto X_k\) および \(y_n \mapsto Y_k\) を行った上で

\[ \hat{S}_{xy, k} = X_k^* Y_k \]

とします。PSDの場合と同様にウェルチの方法（セグメント毎に窓関数をかけて計算したものを平均）がよく用いられ、 scipy.signal.csd もウェルチの方法で実装されています（というより、内部的には scipy.signal.welch は scipy.signa.csd を呼ぶ形で実装されています）。

コヒーレンスについても同様で、 scipy.signal.coherence は \(S_{xy}\), \(S_x\), \(S_y\) のそれぞれをウェルチの方法で推定した上で定義式にプラグインしたものを計算しています。

例（CSDとコヒーレンスの推定）#

離散時間信号 \(x_n\) を入力すると

\[ y_n = 1.414 ( x_n - x_{n - 1} ) + \sin ( 2 \pi \cdot 23 t) \]

を出力する線形システムを考えます。このシステムに信号

\[ x ( t ) = \sin ( 2 \pi \cdot 7 t ) - \cos ( 2 \pi \cdot 13 t ) \]

を \(t = n / 100\) として標本化して入力した場合に、入出力信号間のCSDとコヒーレンスを計算してみましょう。

from scipy.signal import csd, coherence

np.random.seed(42)

t = np.arange(-5, 5, 0.01)  # -5 <= t < 5 の範囲で0.01刻みでサンプリング (1000時刻分)
x = np.sin(2.0 * pi * 7.0 * t) - np.cos(
    2.0 * pi * 13.0 * t
)  # 入力信号；2つの周期成分を持つ関数
y = (
    1.414 * (x[1:] - x[:(-1)])
    + np.sin(2.0 * pi * 23.0 * t[1:])
    + np.random.normal(scale=0.1, size=t[1:].shape)
)  # 出力信号；入力信号の差分に別の正弦波を印加

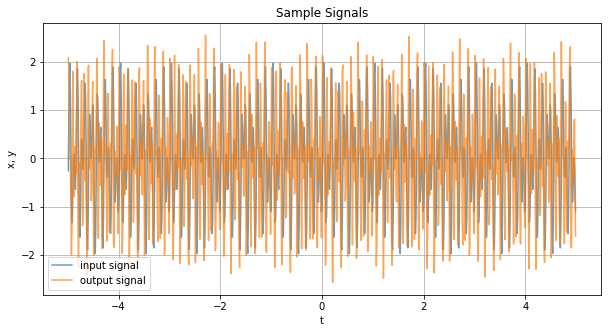
fig, ax = plt.subplots(figsize=(10, 5))

ax.plot(t[1:], x[1:], label="input signal", c="C0", alpha=0.7)
ax.plot(t[1:], y, label="output signal", c="C1", alpha=0.7)
ax.set_title("Sample Signals")
ax.set_xlabel("t")
ax.set_ylabel("x, y")
ax.grid()
ax.legend()

<matplotlib.legend.Legend at 0x13987ba90>
../_images/461bc1bee1d56fca0f8d5c111b7e8a24a624ec71b6d10a7946442bf94eddb186.png 
ff_csd, s_xy = csd(  # CSDの推定を行う関数
    x[1:],  # 1つめの信号（FFTの共役を取る方）
    y,  # 2つめの信号（FFTの共役を取らない方）
    fs=100.0,  # 標本化周波数
    # window='hann',  # 窓関数。デフォルトではハン窓。
    nperseg=128,  # セグメントの長さ。
    # noverlap=None,  # セグメントの重なりの長さ。デフォルトではnpersegの半分。
    # scaling='density',  # 返り値の指定。デフォルトではPSD。 'spectrum' にするとパワースペクトラム。
)
ff_coherence, g_xy = coherence(  # コヒーレンスの推定を行う関数
    x[1:],  # 信号
    y,  #
    fs=100.0,  # 標本化周波数
    # window='hann',  # 窓関数。デフォルトではハン窓。
    nperseg=128,  # セグメントの長さ。
    # noverlap=None,  # セグメントの重なりの長さ。デフォルトではnpersegの半分。
    # scaling='density',  # 返り値の指定。デフォルトではPSD。 'spectrum' にするとパワースペクトラム。
)

fig, axes = plt.subplots(1, 2, figsize=(10, 5))

axes[0].plot(ff_csd, np.abs(s_xy), label="CSD", c="C0")
axes[0].set_title("Estimation of CSD")
axes[0].set_xlabel("frequency")
axes[0].set_ylabel("abs. of CSD")
axes[0].grid()
axes[0].legend()

axes[1].plot(ff_coherence, g_xy, label="coherence", c="C1")
axes[1].set_title("Estimation of Coherence")
axes[1].set_xlabel("frequency")
axes[1].set_ylabel("Coherence")
axes[1].grid()
axes[1].legend()

<matplotlib.legend.Legend at 0x1399325d0>
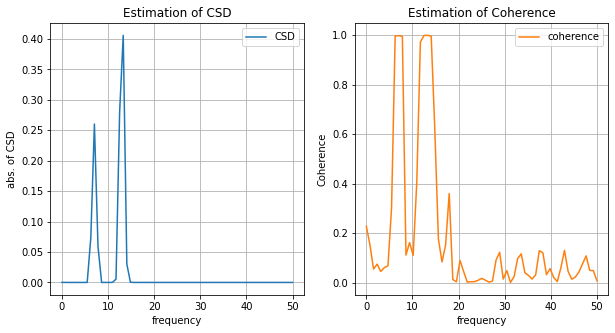
../_images/dc3e5a7c5e8c250208da8a78788a5cc23e0db5d4765364889336be62b3fe1c72.png

CSDとコヒーレンスのいずれも入力信号に含まれる周波数成分 \(f = 7, 13\) の周辺でのみ高い値を取り、逆にシステムによって印加される周波数成分 \(f = 23\) の周りでは消えています。このようなこともあり、コヒーレンスはしばしば周波数領域で入出力信号間の因果関係を測る指標としても利用されています。

時変信号のスペクトル解析#

定常でない信号においては時刻 \(t\) によって信号に含まれる周波数成分が異なるため、それぞれの周波数成分の強さを時刻 \(t\) ごとに計算したものがよく利用されます。これは一般に信号 \(x ( t )\) を窓函数に通して周波数スペクトルを求めるという方法で計算され、この結果、あるいはそれをプロットしたグラフを スペクトログラム (spectrogram) と呼びます。特に離散時間信号では \(x_n\) をSTFTした \(X_{m, k}\) の絶対値の2乗

\[ \left| X_{m, k} \right|^2 \]

（ パワースペクトル (power spectrum) とも）を並べたものをスペクトログラムと呼ぶことが一般的です。

例（周波数成分が変化する関数のスペクトログラム）#

STFTの例と同じく、次の連続時間信号

\[ x ( t ) = \frac{\exp (- \beta t)}{1 + \exp (- \beta t)} \sin (2 \pi f_0 t) + \frac{1}{1 + \exp (- \beta t)} \sin (2 \pi f_1 t) \]

が \(-10 \le t < 10\) において標本化周波数 \(f_s = 100\) で標本化されているものとします。

beta = 0.4
f0 = 15.0
f1 = 10.0

tt = np.arange(
    -10.0, 10.0, 0.01
)  # -10 <= t < 10 の範囲で0.01刻みでサンプリング (2000時刻分)
xx = (1.0 - expit(beta * tt)) * np.sin(2.0 * pi * f0 * tt) + expit(beta * tt) * np.cos(
    2.0 * pi * f1 * tt
)  # 元の信号

この信号 xx のスペクトログラムは scipy.signal の spectrogram で計算できます。標本化周波数のみ指定して、それ以外はデフォルトの値のままで実行してみましょう。

from scipy.signal import spectrogram

f, t, Sxx = spectrogram(  # スペクトログラムの計算を行う関数
    xx,  # 離散時間信号；デフォルトではFFT等の必要に応じて末尾にzero-paddingされる
    fs=100.0,  # 標本化周波数
    # window=('tukey', 0.25),  # 窓関数の種類；デフォルトではTukey窓
    # nperseg=None,  # Nの値；デフォルトでは256が選択される
    # noverlap=None,  # Hの値；デフォルトではN/8
    # detrend='constant',  # デフォルトでは信号の値をそのまま用いず、フレームごとに平均値を差し引いた値を用いる
    # scaling='density',  # スペクトログラムの値を計算するためにPSDの推定を行う
    # mode='psd',  # スペクトログラムの値としてPSDの推定値を返す
)

関数 spectrogram の返り値は3つ組のタプルになっており、順に

  • f: STFTで検出される周波数の第 \(k\) 成分の値を格納したNumPy配列

  • t: STFTで用いる第 \(m\) フレームの中心となる時刻を格納したNumPy配列

  • Sxx: スペクトログラムの値で、 (f.shape[0], t.shape[0])-shapedの複素数値NumPy配列

となっています。関数 stft のデフォルトの設定では信号の先頭と末尾に適当なzero-paddingが行われますが、 spectrogram ではいずれも行われないことに注意してください。

plt.pcolormesh(t - 10.0, f, np.abs(Sxx), vmin=0.0, vmax=1.0, shading="gouraud")
plt.title("Spectrogram (PSD)")
plt.ylabel("Frequency [Hz]")
plt.xlabel("Time [sec]")
plt.show()
../_images/3e6f797adc0eb9542d6a9bb39637351902ff9dbb27104591b4ef53fe38e5c9a0.png

この結果が stft から計算したものと一致するかどうかを確認しておきましょう。

f_stft, t_stft, Zxx = stft(  # STFTを行う関数
    xx,  # 離散時間信号；デフォルトではFFT等の必要に応じて末尾にzero-paddingされる
    fs=100.0,  # 標本化周波数
    window=("tukey", 0.25),  # 窓関数の種類；spectrogramと同様にTukey窓を選択
    nperseg=256,  # Nの値；spectrogramと同様に設定
    noverlap=256 // 8,  # Hの値；spectrogramと同様に設定
    detrend="constant",  # spectrogramと同様に、フレームごとに値の平均を差し引く
    boundary=None,  # spectrogramと同様に、最初のフレームの中心を信号の先頭に合わせるためのpaddingを行わない
    padded=False,  # spectrogramと同様に、最後のフレームが信号の末尾を含むようにするためのpaddingを行わない
)

print(f"周波数の目盛りが一致: {np.isclose(f, f_stft).all()}")
print(f"時間の目盛りが一致: {np.isclose(t, t_stft).all()}")
print(f"値が一致: {np.isclose(Sxx, np.abs(Zxx) ** 2). all()}")

周波数の目盛りが一致: True
時間の目盛りが一致: True
値が一致: False

値が一致しません。これは spectrogram 関数がデフォルトではスペクトログラムの値としてパワースペクトル密度（PSD; 波の値の単位を \(\text{U}\) として、単位は \(\text{U}^2 / \text{Hz}\) ） を返すようになっており、一般的な定義で使われるパワースペクトル（単位は \(\text{U}^2\) ）を返すようにはなっていないためです。 spectrogram 関数を使って一般的な意味でのスペクトログラムの値を計算するには、（SciPy v1.6.1では）キーワード引数で scaling='spectrum' および mode='magnitude' を指定してSTFTの絶対値を返した上でその値を二乗します。

f_ps, t_ps, Sxx_mag = spectrogram(  # スペクトログラムの計算を行う関数
    xx,  # 離散時間信号；デフォルトではFFT等の必要に応じて末尾にzero-paddingされる
    fs=100.0,  # 標本化周波数
    # window=('tukey', 0.25),  # 窓関数の種類；デフォルトではTukey窓
    # nperseg=None,  # Nの値；デフォルトでは256が選択される
    # noverlap=None,  # Hの値；デフォルトではN/8
    # detrend='constant',  # デフォルトでは信号の値をそのまま用いず、フレームごとに平均値を差し引いた値を用いる
    scaling="spectrum",  # スペクトログラムの値を計算するためにSTFTを行う
    mode="magnitude",  # スペクトログラムの値としてSTFTの絶対値を返す
)

plt.pcolormesh(t_ps - 10.0, f_ps, Sxx_mag**2, vmin=0.0, vmax=1.0, shading="gouraud")
plt.title("Spectrogram (Power Spectrum)")
plt.ylabel("Frequency [Hz]")
plt.xlabel("Time [sec]")
plt.show()
../_images/19245377c09cd32e0f816243f6bd56972e90fbcb18255eca6da3c90ef787db31.png 
print(f"周波数の目盛りが一致: {np.isclose(f_ps, f_stft).all()}")
print(f"時間の目盛りが一致: {np.isclose(t_ps, t_stft).all()}")
print(f"値が一致: {np.isclose(Sxx_mag ** 2, np.abs(Zxx) ** 2). all()}")

周波数の目盛りが一致: True
時間の目盛りが一致: True
値が一致: True

今度は確かに値が一致しています。

補足: パワースペクトルとパワースペクトル密度#

直前の例のように、パワースペクトルとパワースペクトル密度は異なるものです。では、どのように違うのでしょうか。そしてそれぞれどのような場合に利用すべきなのでしょうか？

定義を確認すると、パワースペクトルは信号が離散的な \(2 \pi k / T\) ( \(k = 0, 1, 2, \ldots\) ) などの周波数成分のみから構成されているものと仮定してそれぞれの成分のパワーを求めたもの（よって単位は単に \(\text{U}^2\) ）、パワースペクトル密度は信号が連続的な無数の周波数成分を含むものと仮定してそれを密度関数として表現したもの（よって単位は \(\text{U}^2 / \text{Hz}\) ）となっています。従って、実際に連続的な無数の周波数成分を含む信号のパワースペクトルを形式的に求めようとした場合、その値は周波数方向の分解能によって変化するはずです。白色雑音を用いてこのことを確認してみましょう。

np.random.seed(42)

fs = 1000.0
t = np.arange(
    0, 100, 1.0 / fs
)  # 0 <= t < 100 の範囲で0.001刻みでサンプリング (100000時刻分)
x = np.random.normal(size=t.shape)  # 白色雑音

ff_ps_1, s_ps_1 = periodogram(
    x[:10000],  # 信号
    fs=fs,  # 標本化周波数
    scaling="spectrum",  # 返り値にパワースペクトルを指定
    detrend=False,  # 定数項を予め除外せずに推定
)
ff_psd_1, s_psd_1 = periodogram(
    x[:10000],  # 信号
    fs=fs,  # 標本化周波数
    # scaling='density',  # 返り値の指定（デフォルトではPSD）
    detrend=False,  # 定数項を予め除外せずに推定
)
ff_ps_2, s_ps_2 = periodogram(
    x,  # 信号
    fs=fs,  # 標本化周波数
    scaling="spectrum",  # 返り値にパワースペクトルを指定
    detrend=False,  # 定数項を予め除外せずに推定
)
ff_psd_2, s_psd_2 = periodogram(
    x,  # 信号
    fs=fs,  # 標本化周波数
    # scaling='density',  # 返り値の指定（デフォルトではPSD）
    detrend=False,  # 定数項を予め除外せずに推定
)

fig, axes = plt.subplots(1, 2, figsize=(10, 5))

axes[0].plot(ff_ps_1, s_ps_1, alpha=0.7, label="length 1e+5")
axes[0].plot(ff_ps_2, s_ps_2, alpha=0.7, label="length 1e+6")
axes[0].set_yscale("log")
axes[0].set_title("Power Spectrum")
axes[0].legend()

axes[1].plot(ff_psd_1, s_psd_1, alpha=0.7, label="length 1e+5")
axes[1].plot(ff_psd_2, s_psd_2, alpha=0.7, label="length 1e+6")
axes[1].set_yscale("log")
axes[1].set_title("Power Spectral Density")
axes[1].legend()

<matplotlib.legend.Legend at 0x139ae06d0>
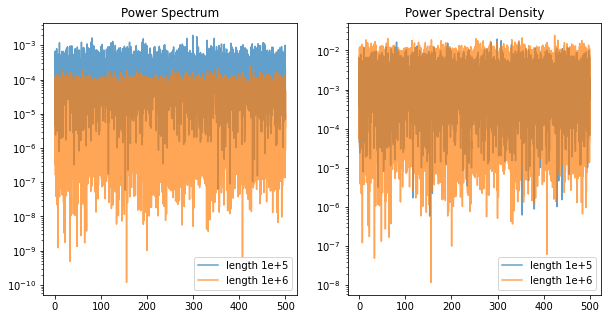
../_images/8564318904985a063f37c23dacc180b8627418b869fb614977c77f6bc1a5d37d.png

関数 periodogram による推定では周波数分解能が信号長に依存します。左側の図はパワースペクトル、右側の図はパワースペクトル密度の推定結果で、いずれも青線は長さ1万、橙線は長さ10万の白色雑音を用いたものです。白色雑音はすべての周波数を連続的に同一の強さで含む信号ですが、パワースペクトルの推定では信号長が10倍になると（即ち、推定の周波数分解能が10倍になると）推定値がおよそ10分の1になっていることが見て取れます。一方、パワースペクトル密度の推定では信号長が10倍になっても推定値のスケールは変化していません。

ほかにも両者の性質の違いは多々ありますが、ひとまず

  • 信号が真に離散的な周波数成分しか含んでいない場合や

  • 周波数分解能が同一のフーリエ変換を通じた結果のみ考える場合

にはパワースペクトルとパワースペクトル密度のどちらを用いても問題ありません。しかし、逆にそうでない場合、即ち

  • 信号が周波数成分を連続的に含んでいる場合や

  • 周波数分解能が異なるフーリエ変換を通じた結果を比較する場合

にはパワースペクトルだと連続的な周波数成分に関する評価を正しく行えない場合があります。

小括#

本項では非定常信号やランダムな信号を周波数領域で取り扱うための手段として短時間フーリエ変換の解説を行い、合わせてスペクトル解析の基礎を概観しました。これらの知見は工場のセンサーデータなど制御が行われているデータを取り扱う上での前提知識として必要となることもあれば、そうでなくとも単に時系列データに対する前処理を行う際に利用されることもあります。周波数解析やスペクトル解析に関する話題は時系列解析・信号処理・制御工学など統計学や工学の幅広い範囲に分散していて（しかもしばしば相互に用語や概念の相違があるため）体系的な学習が困難ですが、もし興味や必要があれば結局はそれぞれの分野の入門書を地道に当たっていくのが現状では良いと思われます。なお、本項は scipy.signal の実装を軸に解説したため主に信号処理の分野に拠っていますので、後から見返す際にはご注意ください。

参考文献#

目次