正規化

本項では、解析対象のデータを適宜事前に正規化することの必要性を解説します。

重回帰分析やクラスタリングなどの機械学習手法は、通常は複数の列の値を利用します。これらの手法を利用する際に事前に正規化を行わず、列ごとに取り得る値の範囲（スケール）が大きく異なると問題が発生する場合があります。例えば次のような場合が考えられます。

【重回帰分析に正則化を適用する場合】

正則化とは、機械学習モデルを学習する際に過学習が発生するのを防ぐための仕組みです（正則化に関する詳細はまたどこかで）。
過学習が発生しているときは、特定の入力値に対する機械学習のモデルの係数が不必要に大きくなる傾向があります。正則化はその傾向を利用し、モデルの係数が大きいほど学習時にペナルティを与えて機械学習のモデルの係数をなるべく小さくしようとします。
しかし、入力値の列ごとに取り得る範囲が大きく異なると、過学習の発生に関係なく、各入力値に対応するモデルの係数のスケールも大きく異なり、正則化が正常に作用しなくなってしまいます。
例えば、予測値に対して同程度の影響を与えている２つの列、AとBがあり、A列の値が10程度の値をとるのに対してB列の値は100程度の値をとることにします。このときAとBが同程度に予測に影響力がある場合では、A列に対する予測モデルの係数はB列に対する予測モデルの係数の10倍程度になってしまいます。この状態で正則化を適用すると、A列に対する予測モデルの係数を不当に下げようとしてしまいます。

【クラスタリングによる分類の場合】
多くのクラスタリング手法では各データの複数の列の値からデータ間の距離を定義し、データの類似性を計算します。そのため、もし入力値の取り得る範囲が大きく異なると、取り得る範囲が大きい列の値のみが強く考慮されてしまいます。

正規化とは、数値の取り得る範囲を揃える変換処理を指します。さまざまな種類の正規化がありますが、本項ではその中でも一般的な２つの正規化について紹介します。

準備

import warnings

warnings.filterwarnings("ignore")

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

# matplotlibでは日本語にデフォルトで対応していないので、日本語対応フォントを読み込む
plt.rcParams["font.family"] = "BIZ UDGothic"  # Windows
# plt.rcParams['font.family'] = 'Hiragino Maru Gothic Pro' # Mac

# その他使えるフォント一覧は以下のコードで取得できます。
# import matplotlib.font_manager
# [f.name for f in matplotlib.font_manager.fontManager.ttflist]

# 使用するデータの読み込み
fpath = "../data/2020413.csv"
df = pd.read_csv(fpath, index_col=0, parse_dates=True, encoding="shift-jis")

紙面の都合上、分散が大きい順にソートして、ソート順で等間隔に10カラムを使用することとする。
※ただし、分散0.0のカラムは除く

df = df.loc[:, df.std(axis=0) > 0.0]
use_list = (
    df.describe()
    .sort_values(by=["std"], ascending=False, axis=1)
    .iloc[:, :: int(df.shape[1] / 10)]
    .columns
)
df = df[use_list]

df.head()

	蒸留塔リボイラー熱量_MV	コンプレッサー出口温度_PV	反応器外殻温度_MV	熱交換器入口流量（製品ガス）_PV	有機生成物レベル_SV	アブソーバ液体排出量_MV	アブソーバ還流流量_MV (Fixed)	リサイクルガス組成（C2H6）_PV	反応器流入組成（O2）_PV	反応器流入組成（H2O）_PV	リサイクルガス組成（H2O）_PV	気化器液体流入量_MV (Fixed)
2020-04-13 00:00:00	67178.857911	80.883014	135.018392	18.832094	0.55	1.213667	0.766	0.248607	0.074659	0.008524	0.000894	2.1924
2020-04-13 00:00:01	67178.857911	80.829548	135.018392	18.884095	0.55	1.213667	0.766	0.249256	0.075105	0.008512	0.000894	2.1924
2020-04-13 00:00:02	60582.821045	80.904742	134.778196	19.199430	0.55	1.214526	0.756	0.249171	0.074506	0.008541	0.000894	2.1924
2020-04-13 00:00:03	57729.202947	80.835981	134.603321	18.862606	0.55	1.214776	0.746	0.249289	0.075398	0.008573	0.000894	2.1924
2020-04-13 00:00:04	54815.597151	80.754689	134.497927	18.738535	0.55	1.214362	0.766	0.249102	0.075198	0.008547	0.000893	2.1924

df.tail()

	蒸留塔リボイラー熱量_MV	コンプレッサー出口温度_PV	反応器外殻温度_MV	熱交換器入口流量（製品ガス）_PV	有機生成物レベル_SV	アブソーバ液体排出量_MV	アブソーバ還流流量_MV (Fixed)	リサイクルガス組成（C2H6）_PV	反応器流入組成（O2）_PV	反応器流入組成（H2O）_PV	リサイクルガス組成（H2O）_PV	気化器液体流入量_MV (Fixed)
2020-04-13 23:59:56	66257.021889	82.785892	136.876003	18.567308	0.55	1.188646	0.756	0.254027	0.078445	0.008531	0.000876	2.1924
2020-04-13 23:59:57	66894.702397	82.746316	136.888292	18.945784	0.55	1.189685	0.766	0.254475	0.077909	0.008509	0.000878	2.1924
2020-04-13 23:59:58	66050.425167	82.892869	136.924143	19.239359	0.55	1.188772	0.756	0.255390	0.077610	0.008557	0.000880	2.1924
2020-04-13 23:59:59	67405.594628	82.783336	136.893139	19.107552	0.55	1.189255	0.756	0.255019	0.078188	0.008597	0.000877	2.1924
2020-04-14 00:00:00	68846.232296	82.809465	136.903559	18.948004	0.55	1.188527	0.766	0.254780	0.078324	0.008595	0.000880	2.1924

df.describe()

	蒸留塔リボイラー熱量_MV	コンプレッサー出口温度_PV	反応器外殻温度_MV	熱交換器入口流量（製品ガス）_PV	有機生成物レベル_SV	アブソーバ液体排出量_MV	アブソーバ還流流量_MV (Fixed)	リサイクルガス組成（C2H6）_PV	反応器流入組成（O2）_PV	反応器流入組成（H2O）_PV	リサイクルガス組成（H2O）_PV	気化器液体流入量_MV (Fixed)
count	86401.000000	86401.000000	86401.000000	86401.000000	86401.000000	86401.000000	86401.000000	86401.000000	86401.000000	86401.000000	86401.000000	8.640100e+04
mean	67668.330180	80.914163	135.968373	18.866493	0.484244	1.202388	0.755994	0.251881	0.077672	0.008527	0.000882	2.192400e+00
std	1381.164212	3.155376	1.016810	0.249775	0.082793	0.022769	0.015588	0.002792	0.001410	0.000216	0.000049	9.237109e-14
min	54815.597151	74.852413	134.348692	17.823561	0.380000	1.158150	0.726000	0.243355	0.073168	0.008062	0.000785	2.192400e+00
25%	66552.782054	78.256071	134.709236	18.697833	0.380000	1.181903	0.746000	0.250097	0.076724	0.008393	0.000851	2.192400e+00
50%	67669.766877	81.320922	136.479395	18.866601	0.550000	1.203074	0.756000	0.251735	0.077651	0.008490	0.000877	2.192400e+00
75%	68805.425973	83.795961	136.646186	19.035252	0.550000	1.218278	0.766000	0.253493	0.078719	0.008639	0.000917	2.192400e+00
max	72154.313660	85.342873	139.550278	19.947215	0.550000	1.280589	0.786000	0.260365	0.082289	0.009316	0.001011	2.192400e+00

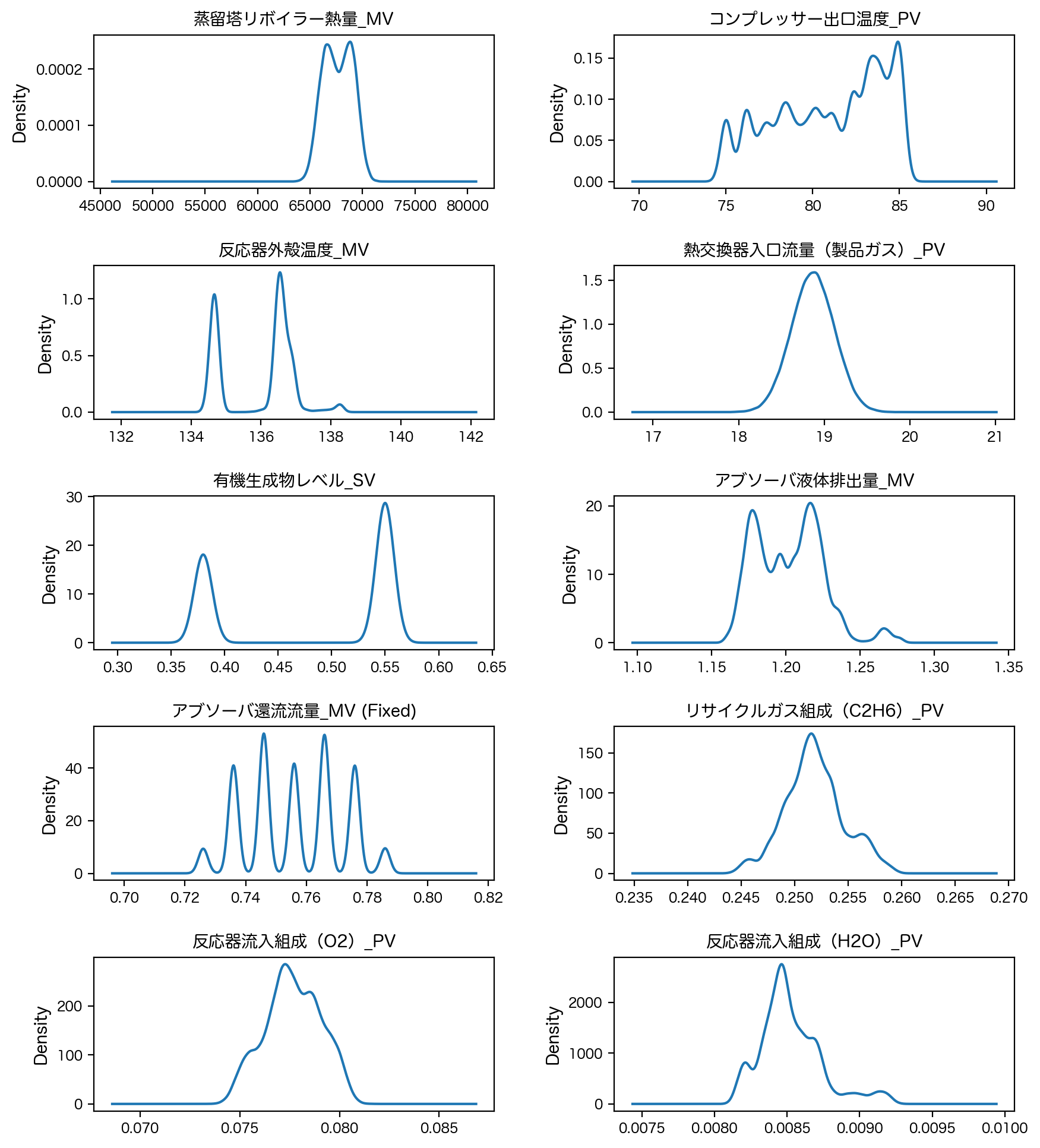
元のデータの密度関数

fig, axes = plt.subplots(5, 2, figsize=(10, 12), dpi=200)
plt.subplots_adjust(hspace=0.5, wspace=0.3)
for ax, label in zip(axes.flatten(), df.columns):
    ax = df[label].plot.kde(ax=ax, legend=False, fontsize=8)
    ax.set_title(label, fontsize=10)

平均0、分散1に変換する正規化

\[ \mathrm{StandardScaler}(x)=\frac{x-\mathrm{mean}(x)}{\mathrm{std}(x)} \]

時系列データ分析ではよく利用される正規化方法です。より厳密には、元のデータの特性や分布を考慮して、正規化の方法を使い分けられることが理想ですが、真剣に取り組むと非常に難しい問題です。

from sklearn.preprocessing import StandardScaler

# 正規化を行うオブジェクトを生成
ss = StandardScaler()

# fit_transform関数は、fit関数（正規化するための前準備の計算）と
# transform関数（準備された情報から正規化の変換処理を行う）の両方を行う
df_normalized_ss = pd.DataFrame(ss.fit_transform(df), columns=df.columns)

df_normalized_ss.head()

	蒸留塔リボイラー熱量_MV	コンプレッサー出口温度_PV	反応器外殻温度_MV	熱交換器入口流量（製品ガス）_PV	有機生成物レベル_SV	アブソーバ液体排出量_MV	アブソーバ還流流量_MV (Fixed)	リサイクルガス組成（C2H6）_PV	反応器流入組成（O2）_PV	反応器流入組成（H2O）_PV	リサイクルガス組成（H2O）_PV	気化器液体流入量_MV (Fixed)
0	-0.354393	-0.009872	-0.934281	-0.137722	0.794224	0.495359	0.641887	-1.172311	-2.136527	-0.016582	0.247364	1.0
1	-0.354393	-0.026816	-0.934281	0.070473	0.794224	0.495359	0.641887	-0.939788	-1.820098	-0.072342	0.239438	1.0
2	-5.130129	-0.002986	-1.170508	1.332956	0.794224	0.533095	0.000379	-0.970490	-2.244756	0.064777	0.246981	1.0
3	-7.196237	-0.024778	-1.342492	-0.015561	0.794224	0.544086	-0.641130	-0.928063	-1.612261	0.212374	0.253573	1.0
4	-9.305778	-0.050541	-1.446145	-0.512295	0.794224	0.525894	0.641887	-0.995215	-1.754583	0.090572	0.237569	1.0

df_normalized_ss.tail()

	蒸留塔リボイラー熱量_MV	コンプレッサー出口温度_PV	反応器外殻温度_MV	熱交換器入口流量（製品ガス）_PV	有機生成物レベル_SV	アブソーバ液体排出量_MV	アブソーバ還流流量_MV (Fixed)	リサイクルガス組成（C2H6）_PV	反応器流入組成（O2）_PV	反応器流入組成（H2O）_PV	リサイクルガス組成（H2O）_PV	気化器液体流入量_MV (Fixed)
86396	-1.021831	0.593191	0.892630	-1.197824	0.794224	-0.603569	0.000379	0.768853	0.548032	0.016202	-0.126012	1.0
86397	-0.560131	0.580648	0.904716	0.317452	0.794224	-0.557954	0.641887	0.929215	0.167724	-0.087141	-0.085764	1.0
86398	-1.171413	0.627094	0.939976	1.492816	0.794224	-0.598017	0.000379	1.256924	-0.044264	0.135896	-0.039164	1.0
86399	-0.190229	0.592381	0.909483	0.965109	0.794224	-0.576825	0.000379	1.123960	0.365867	0.320600	-0.095534	1.0
86400	0.852838	0.600661	0.919731	0.326339	0.794224	-0.608778	0.641887	1.038424	0.462367	0.314475	-0.047932	1.0

df_normalized_ss.describe()

	蒸留塔リボイラー熱量_MV	コンプレッサー出口温度_PV	反応器外殻温度_MV	熱交換器入口流量（製品ガス）_PV	有機生成物レベル_SV	アブソーバ液体排出量_MV	アブソーバ還流流量_MV (Fixed)	リサイクルガス組成（C2H6）_PV	反応器流入組成（O2）_PV	反応器流入組成（H2O）_PV	リサイクルガス組成（H2O）_PV	気化器液体流入量_MV (Fixed)
count	8.640100e+04	8.640100e+04	8.640100e+04	8.640100e+04	8.640100e+04	8.640100e+04	8.640100e+04	8.640100e+04	8.640100e+04	8.640100e+04	8.640100e+04	86401.0
mean	-1.672532e-14	-1.626818e-15	2.073581e-14	-4.383406e-15	6.132897e-14	-2.759025e-15	-8.087020e-15	1.124173e-15	7.007887e-16	4.923589e-15	2.150416e-15	1.0
std	1.000006e+00	1.000006e+00	1.000006e+00	1.000006e+00	1.000006e+00	1.000006e+00	1.000006e+00	1.000006e+00	1.000006e+00	1.000006e+00	1.000006e+00	0.0
min	-9.305778e+00	-1.921098e+00	-1.592913e+00	-4.175512e+00	-1.259090e+00	-1.942974e+00	-1.924147e+00	-3.053367e+00	-3.193416e+00	-2.155344e+00	-1.989776e+00	1.0
25%	-8.076915e-01	-8.424060e-01	-1.238328e+00	-6.752532e-01	-1.259090e+00	-8.997394e-01	-6.411300e-01	-6.387418e-01	-6.723666e-01	-6.219211e-01	-6.334459e-01	1.0
50%	1.040213e-03	1.289105e-01	5.025768e-01	4.312509e-04	7.942243e-01	3.012443e-02	3.786639e-04	-5.209853e-02	-1.491356e-02	-1.727655e-01	-1.003733e-01	1.0
75%	8.232927e-01	9.133031e-01	6.666114e-01	6.756474e-01	7.942243e-01	6.978819e-01	6.418873e-01	5.774905e-01	7.422012e-01	5.161618e-01	7.175185e-01	1.0
max	3.247991e+00	1.403552e+00	3.522710e+00	4.326810e+00	7.942243e-01	3.434622e+00	1.924905e+00	3.038621e+00	3.273125e+00	3.652417e+00	2.640463e+00	1.0

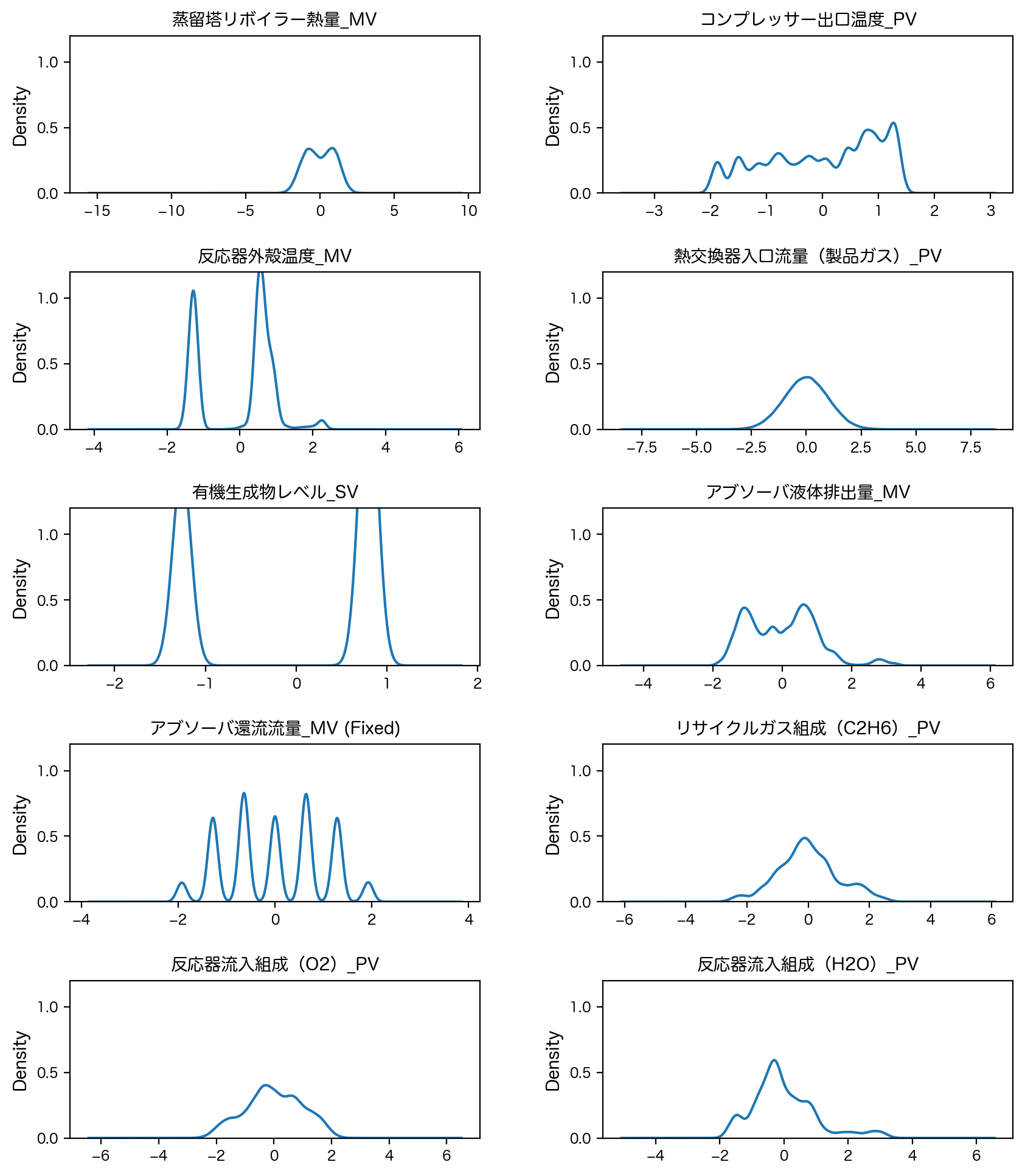
正規化後の密度関数（平均0、分散1）

縦軸のスケールを揃えている点に注意

# StandardScaler後の密度関数
fig, axes = plt.subplots(5, 2, figsize=(10, 12), dpi=200)
plt.subplots_adjust(hspace=0.5, wspace=0.3)
for ax, label in zip(axes.flatten(), df_normalized_ss.columns):
    ax = df_normalized_ss[label].plot.kde(ax=ax, legend=False, fontsize=8)
    ax.set_title(label, fontsize=10)
    ax.set_ylim(0, 1.2)

最小値0、最大値1に変換する正規化

\[ \mathrm{MinMaxScaler}(x)=\frac{x-\mathrm{min}(x)}{\mathrm{max}(x)-\mathrm{min}(x)} \]

事前に値域が明らかな場合やデータが一様分布に従ってそうな場合に、よく用いられる正規化手法です。例えば、画像データでは、画素値が[0, 255] に規定されており、扱いやすくするために[0, 1]に正規化します。

ここでは時系列データに対して、最小値-最大値による正規化を行った例を示します。

from sklearn.preprocessing import MinMaxScaler

# 正規化を行うオブジェクトを生成
mm = MinMaxScaler()

# fit_transform関数は、fit関数（正規化するための前準備の計算）と
# transform関数（準備された情報から正規化の変換処理を行う）の両方を行う
df_normalized_mm = pd.DataFrame(mm.fit_transform(df), columns=df.columns)

df_normalized_mm.head()

	蒸留塔リボイラー熱量_MV	コンプレッサー出口温度_PV	反応器外殻温度_MV	熱交換器入口流量（製品ガス）_PV	有機生成物レベル_SV	アブソーバ液体排出量_MV	アブソーバ還流流量_MV (Fixed)	リサイクルガス組成（C2H6）_PV	反応器流入組成（O2）_PV	反応器流入組成（H2O）_PV	リサイクルガス組成（H2O）_PV	気化器液体流入量_MV (Fixed)
0	0.713044	0.574865	0.128749	0.474904	1.0	0.453424	0.666667	0.308775	0.163440	0.368259	0.483159	0.0
1	0.713044	0.569769	0.128749	0.499391	1.0	0.453424	0.666667	0.346944	0.212373	0.358658	0.481447	0.0
2	0.332621	0.576937	0.082572	0.647878	1.0	0.460442	0.500000	0.341904	0.146703	0.382268	0.483076	0.0
3	0.168040	0.570382	0.048952	0.489272	1.0	0.462485	0.333333	0.348869	0.244513	0.407682	0.484500	0.0
4	0.000000	0.562633	0.028690	0.430849	1.0	0.459103	0.666667	0.337846	0.222504	0.386710	0.481043	0.0

df_normalized_mm.tail()

	蒸留塔リボイラー熱量_MV	コンプレッサー出口温度_PV	反応器外殻温度_MV	熱交換器入口流量（製品ガス）_PV	有機生成物レベル_SV	アブソーバ液体排出量_MV	アブソーバ還流流量_MV (Fixed)	リサイクルガス組成（C2H6）_PV	反応器流入組成（O2）_PV	反応器流入組成（H2O）_PV	リサイクルガス組成（H2O）_PV	気化器液体流入量_MV (Fixed)
86396	0.659877	0.756257	0.485873	0.350221	1.0	0.249071	0.500000	0.627417	0.578586	0.373904	0.402520	0.0
86397	0.696655	0.752484	0.488236	0.528440	1.0	0.257554	0.666667	0.653741	0.519774	0.356110	0.411213	0.0
86398	0.647962	0.766454	0.495128	0.666680	1.0	0.250104	0.500000	0.707534	0.486992	0.394514	0.421277	0.0
86399	0.726120	0.756013	0.489167	0.604614	1.0	0.254045	0.500000	0.685708	0.550415	0.426316	0.409102	0.0
86400	0.809208	0.758504	0.491171	0.529485	1.0	0.248103	0.666667	0.671668	0.565338	0.425262	0.419383	0.0

df_normalized_mm.describe()

	蒸留塔リボイラー熱量_MV	コンプレッサー出口温度_PV	反応器外殻温度_MV	熱交換器入口流量（製品ガス）_PV	有機生成物レベル_SV	アブソーバ液体排出量_MV	アブソーバ還流流量_MV (Fixed)	リサイクルガス組成（C2H6）_PV	反応器流入組成（O2）_PV	反応器流入組成（H2O）_PV	リサイクルガス組成（H2O）_PV	気化器液体流入量_MV (Fixed)
count	86401.000000	86401.000000	86401.000000	86401.000000	86401.000000	86401.000000	86401.000000	86401.000000	86401.000000	86401.000000	86401.000000	86401.0
mean	0.741274	0.577835	0.311382	0.491103	0.613199	0.361309	0.499902	0.501210	0.493837	0.371114	0.429735	0.0
std	0.079658	0.300785	0.195481	0.117616	0.487020	0.185958	0.259806	0.164151	0.154643	0.172184	0.215973	0.0
min	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.0
25%	0.676935	0.324453	0.069314	0.411683	0.000000	0.193996	0.333333	0.396361	0.389861	0.264030	0.292929	0.0
50%	0.741356	0.616609	0.409626	0.491153	1.000000	0.366911	0.500000	0.492658	0.491531	0.341367	0.408057	0.0
75%	0.806855	0.852541	0.441691	0.570569	1.000000	0.491085	0.666667	0.596005	0.608612	0.459989	0.584699	0.0
max	1.000000	1.000000	1.000000	1.000000	1.000000	1.000000	1.000000	1.000000	1.000000	1.000000	1.000000	0.0

正規化後の密度関数（最小値0、最大値1）

縦軸のスケールを揃えている点に注意

# MinMaxScaler後の密度関数
fig, axes = plt.subplots(5, 2, figsize=(10, 12), dpi=200)
plt.subplots_adjust(hspace=0.5, wspace=0.3)
for ax, label in zip(axes.flatten(), df_normalized_mm.columns):
    ax = df_normalized_mm[label].plot.kde(ax=ax, legend=False, fontsize=8)
    ax.set_title(label, fontsize=10)
    ax.set_ylim(0, 13.0)

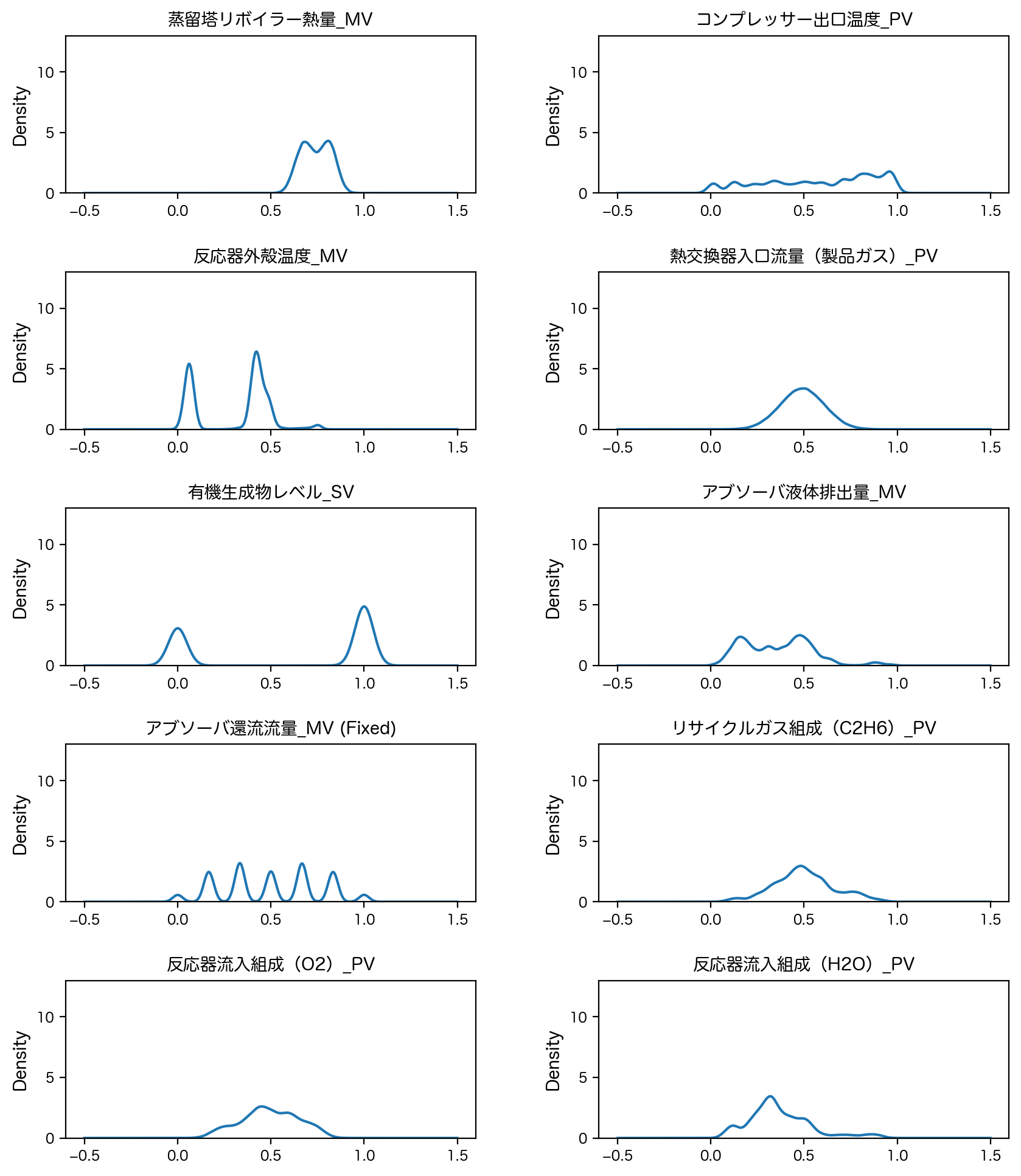
例えば 蒸留塔リボイラー熱量_MV に注目してみると、0〜1に正規化したにも関わらず、ほとんどの要素が0.5〜1付近に偏っていることがわかります。また、 反応器外殻温度_MV は、0〜0.5付近に偏っています。これは、外れ値（わずか数点だけ非常に大きい値をとるデータが混在）の影響を受けているためだと考えられます。冒頭で説明したように正規化の主要な目的は、列ごとに取り得る値の範囲を同じスケールに揃えることですが、これでは少なくとも 蒸留塔リボイラー熱量_MV と 反応器外殻温度_MV で取り得る値の範囲が異なってしまっているため、スケール違いの影響は依然残ったままと言えるかもしれません。

小括

本項ではデータの正規化方法と必要性について紹介しました。特殊な状況を考えていないのであれば、平均0、分散1で正規化するのがベターだと思います。
最小値0、最大値1の正規化は、元のデータの特性や分布を考慮して、例えばデータが一様分布に従ってそうな場合などでは有効な手法です。

参考文献

• 前処理大全 ［データ分析のためのSQL/R/Python実践テクニック］ 第8章 数値型 8-4 正規化