次元圧縮(後編:その他の手法)#
※機械学習の文脈の「次元削減」や「次元圧縮」は日本語に多少ブレがあります。
ここでは高次元空間上のデータについて、
列の要素に変更は加えず、個々の列(軸)を削減することで低次元化を達成する手法を「次元削減」(VIFなど)
列の要素の変換も伴うような、何らかの写像によって低次元空間に射影する手法を「次元圧縮」(PCAなど)
と呼ぶことにします。
本項では「次元圧縮」についてまとめます。
データの読み込み#
データの読み込みに関しては次元削減で行った手法と同一です。
import warnings
warnings.filterwarnings('ignore')
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
pd.set_option("display.max_rows", 10)
pd.set_option("display.max_columns", 10)
# matplotlibでは日本語にデフォルトで対応していないので、日本語対応フォントを読み込む
plt.rcParams['font.family'] = 'BIZ UDGothic' # Windows
# plt.rcParams['font.family'] = 'Hiragino Maru Gothic Pro' # Mac
# 使えるフォント一覧は以下のコードで取得できます。
# import matplotlib.font_manager
# [f.name for f in matplotlib.font_manager.fontManager.ttflist]
fpath = '../data/2020413.csv'
df = pd.read_csv(fpath, index_col = 0, parse_dates = True, encoding = 'shift-jis')[::10]
数値型の要約統計量
df.describe()
| 気化器圧力_PV | 気化器圧力_SV | 気化器圧力_MV | 気化器液面レベル_PV | 気化器液面レベル_SV | ... | 反応器流入組成(HAc)_PV | セパレータ蒸気排出量_MV (Fixed) | アブソーバスクラブ流量_MV (Fixed) | アブソーバ還流流量_MV (Fixed) | 気化器液体流入量_MV (Fixed) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 8641.000000 | 8641.000000 | 8641.000000 | 8641.000000 | 8.641000e+03 | ... | 8641.000000 | 8641.0000 | 8641.000000 | 8641.000000 | 8.641000e+03 |
| mean | 128.006452 | 128.003415 | 18.739506 | 0.699816 | 7.000000e-01 | ... | 0.109533 | 16.1026 | 15.119916 | 0.755890 | 2.192400e+00 |
| std | 0.732346 | 0.526849 | 0.270095 | 0.001444 | 1.110287e-16 | ... | 0.000586 | 0.0000 | 0.018634 | 0.015684 | 4.441149e-16 |
| min | 125.347772 | 126.183125 | 17.867357 | 0.692315 | 7.000000e-01 | ... | 0.107120 | 16.1026 | 14.119800 | 0.726000 | 2.192400e+00 |
| 25% | 127.519430 | 127.640924 | 18.558258 | 0.699342 | 7.000000e-01 | ... | 0.109155 | 16.1026 | 15.119800 | 0.746000 | 2.192400e+00 |
| 50% | 128.026204 | 128.028863 | 18.737580 | 0.699988 | 7.000000e-01 | ... | 0.109522 | 16.1026 | 15.119800 | 0.756000 | 2.192400e+00 |
| 75% | 128.517488 | 128.401727 | 18.920620 | 0.700583 | 7.000000e-01 | ... | 0.109899 | 16.1026 | 15.119800 | 0.766000 | 2.192400e+00 |
| max | 130.392239 | 129.356617 | 19.774625 | 0.704532 | 7.000000e-01 | ... | 0.112340 | 16.1026 | 16.119800 | 0.786000 | 2.192400e+00 |
8 rows × 91 columns
# 正規化を行う
from sklearn.preprocessing import StandardScaler
# 正規化を行うオブジェクトを生成
ss = StandardScaler()
# fit_transform関数は、fit関数(正規化するための前準備の計算)と
# transform関数(準備された情報から正規化の変換処理を行う)の両方を行う
df = pd.DataFrame(ss.fit_transform(df), index=df.index, columns=df.columns)
さらに分散(標準偏差)が1.0に正規化できなかった列を取り除く
df = df.drop(columns = df.columns[list(df.std(axis=0) < 0.9)]) # 数値計算の誤差を考慮して標準偏差が0.9未満の列を除外
独立成分分析#
【独立成分分析(Independent Component Analysis:ICA)とは】
主成分分析ではデータを低次元化したり、互いに無相関な成分を抽出したりしていました。
しかし、観測データが正規分布に従っていない場合、主成分分析をしてデータは無相関化されたと言っても、それを以て独立であるとは言えません。
そのような場合は独立であるような状態でデータを見たほうが、完全に個々の変量について考察ができて便利な場合も多いです。
独立成分分析では観測データに正規分布を仮定せずに、互いに独立な成分の抽出を目指してデータの低次元化を行います。
主成分分析と独立成分分析は下図のような関係にあります(データ化学工学研究室(金子研究室)@明治大学 理工学部 応用化学科 より引用)。
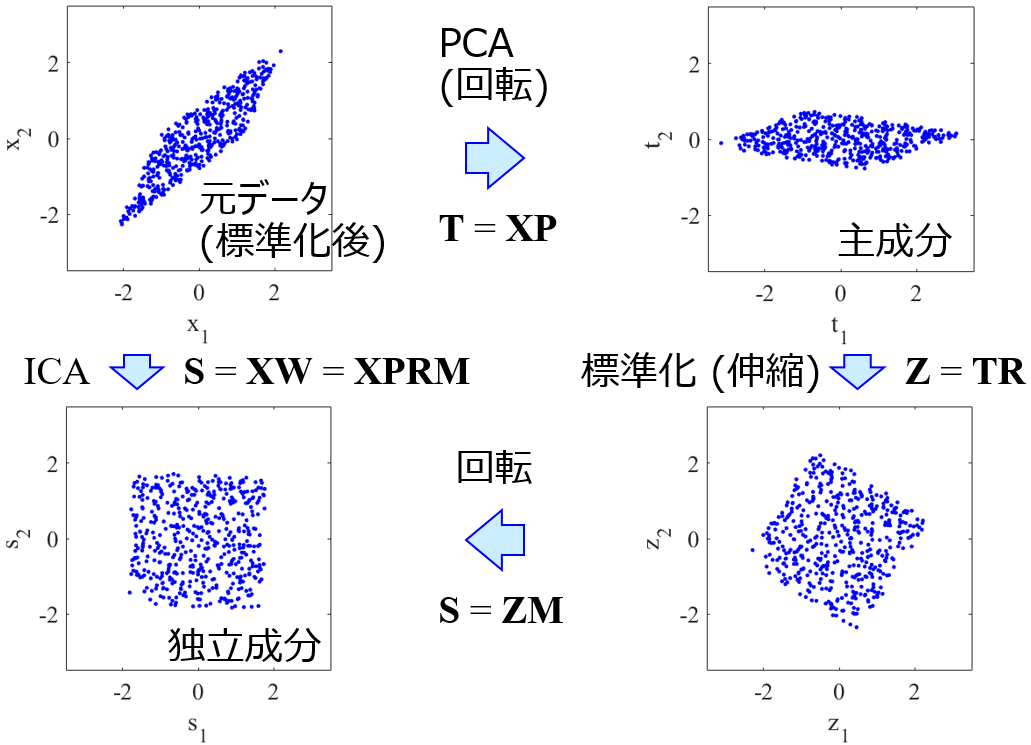
主成分分析
互いに無相関な成分 (主成分) を計算する手法
主成分は寄与率の大きい順に並べることができる
独立成分分析
互いに独立な成分 (独立成分) を計算する手法
独立成分はどれも平等である
独立は無相関より強力
データセット内に外れ値があると、外れ値が強調されたような独立成分が抽出される
ここでは図示の簡単化のため、 気化器圧力_PV と 気化器液面レベル_PV の2つのカラムのみを用います。
まず独立成分分析を行います。
from sklearn.decomposition import FastICA
ica = FastICA(n_components = None, whiten='arbitrary-variance')
ica.fit(df[['気化器圧力_PV','気化器液面レベル_PV']])
ica_transform = ica.transform(df[['気化器圧力_PV','気化器液面レベル_PV']])
pd.DataFrame(ica_transform, index = df.index, columns = ["第"+str(d+1)+"独立成分" for d in range(2)])
| 第1独立成分 | 第2独立成分 | |
|---|---|---|
| 2020-04-13 00:00:00 | 0.001552 | -0.003029 |
| 2020-04-13 00:00:10 | 0.007027 | 0.000893 |
| 2020-04-13 00:00:20 | -0.001592 | 0.000913 |
| 2020-04-13 00:00:30 | 0.005017 | 0.003414 |
| 2020-04-13 00:00:40 | -0.003775 | 0.001856 |
| ... | ... | ... |
| 2020-04-13 23:59:20 | -0.004407 | -0.007352 |
| 2020-04-13 23:59:30 | 0.016208 | 0.005269 |
| 2020-04-13 23:59:40 | -0.012352 | 0.005786 |
| 2020-04-13 23:59:50 | -0.006004 | 0.006723 |
| 2020-04-14 00:00:00 | 0.016881 | -0.004475 |
8641 rows × 2 columns
次に主成分分析も行います。
from sklearn.decomposition import PCA
pca_ = PCA(n_components = None)
pca_.fit(df[['気化器圧力_PV','気化器液面レベル_PV']])
pca_transform = pca_.transform(df[['気化器圧力_PV','気化器液面レベル_PV']])
pd.DataFrame(pca_transform, index = df.index, columns = ["第"+str(d+1)+"主成分" for d in range(2)])
| 第1主成分 | 第2主成分 | |
|---|---|---|
| 2020-04-13 00:00:00 | -0.167893 | -0.212614 |
| 2020-04-13 00:00:10 | 0.547118 | -0.355817 |
| 2020-04-13 00:00:20 | -0.024137 | 0.126927 |
| 2020-04-13 00:00:30 | 0.639049 | -0.138696 |
| 2020-04-13 00:00:40 | -0.084901 | 0.288212 |
| ... | ... | ... |
| 2020-04-13 23:59:20 | -0.951004 | -0.059014 |
| 2020-04-13 23:59:30 | 1.549200 | -0.687404 |
| 2020-04-13 23:59:40 | -0.303479 | 0.931002 |
| 2020-04-13 23:59:50 | 0.202473 | 0.615011 |
| 2020-04-14 00:00:00 | 0.721860 | -1.129753 |
8641 rows × 2 columns
独立成分分析と主成分分析の結果を比較した図が以下のようになります。
plt.figure(figsize = [8,6], dpi = 200)
plt.scatter(df['気化器圧力_PV'], df['気化器液面レベル_PV'])
plt.xlabel('気化器圧力_PV')
plt.ylabel('気化器液面レベル_PV')
plt.xlim(-5,5)
plt.ylim(-5,5)
plt.gca().set_aspect('equal') # 現在の図のアスペクト比を縦横一定に設定
plt.annotate('第1主成分軸', xy = (0,0), xytext = pca_.components_[0]*4.5, xycoords='data', arrowprops=dict(arrowstyle="<-"))
plt.annotate('第2主成分軸', xy = (0,0), xytext = pca_.components_[1]*4.5, xycoords='data', arrowprops=dict(arrowstyle="<-"))
ica_arrow = ica.components_.T/np.linalg.norm(ica.components_.T, axis=0).reshape(-1,1)
plt.annotate('第1独立成分軸', xy = (0,0), xytext = ica_arrow[0]*4.5, xycoords='data', color = 'red', arrowprops=dict(arrowstyle="<-", color = 'red'))
plt.annotate('第2独立成分軸', xy = (0,0), xytext = ica_arrow[1]*4.5, xycoords='data', color = 'red', arrowprops=dict(arrowstyle="<-", color = 'red'))
plt.show()
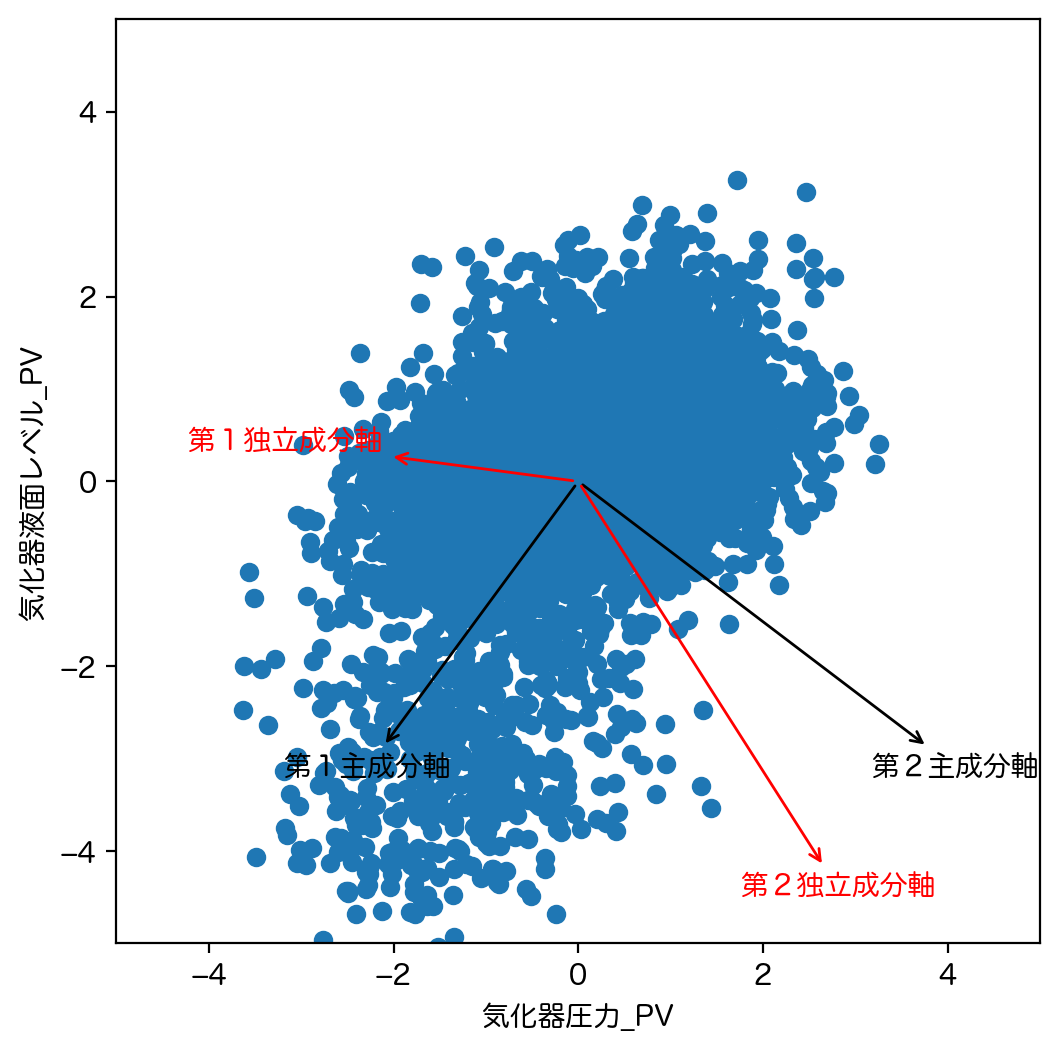
fig = plt.figure(figsize = [12,6], dpi = 200)
subplot = fig.add_subplot(1,2,1)
subplot.set_xlabel('第1主成分軸')
subplot.set_ylabel('第2主成分軸')
subplot.set_title('主成分分析による変換')
subplot.set_xlim(-5,5)
subplot.set_ylim(-5,5)
subplot.set_aspect('equal')
subplot.scatter(pca_transform[:,0], pca_transform[:,1])
subplot = fig.add_subplot(1,2,2)
subplot.set_xlabel('第1独立成分軸')
subplot.set_ylabel('第2独立成分軸')
subplot.set_title('独立成分分析による変換')
subplot.set_xlim(-0.05,0.05)
subplot.set_ylim(-0.05,0.05)
subplot.set_aspect('equal')
subplot.scatter(ica_transform[:,0], ica_transform[:,1])
plt.show()
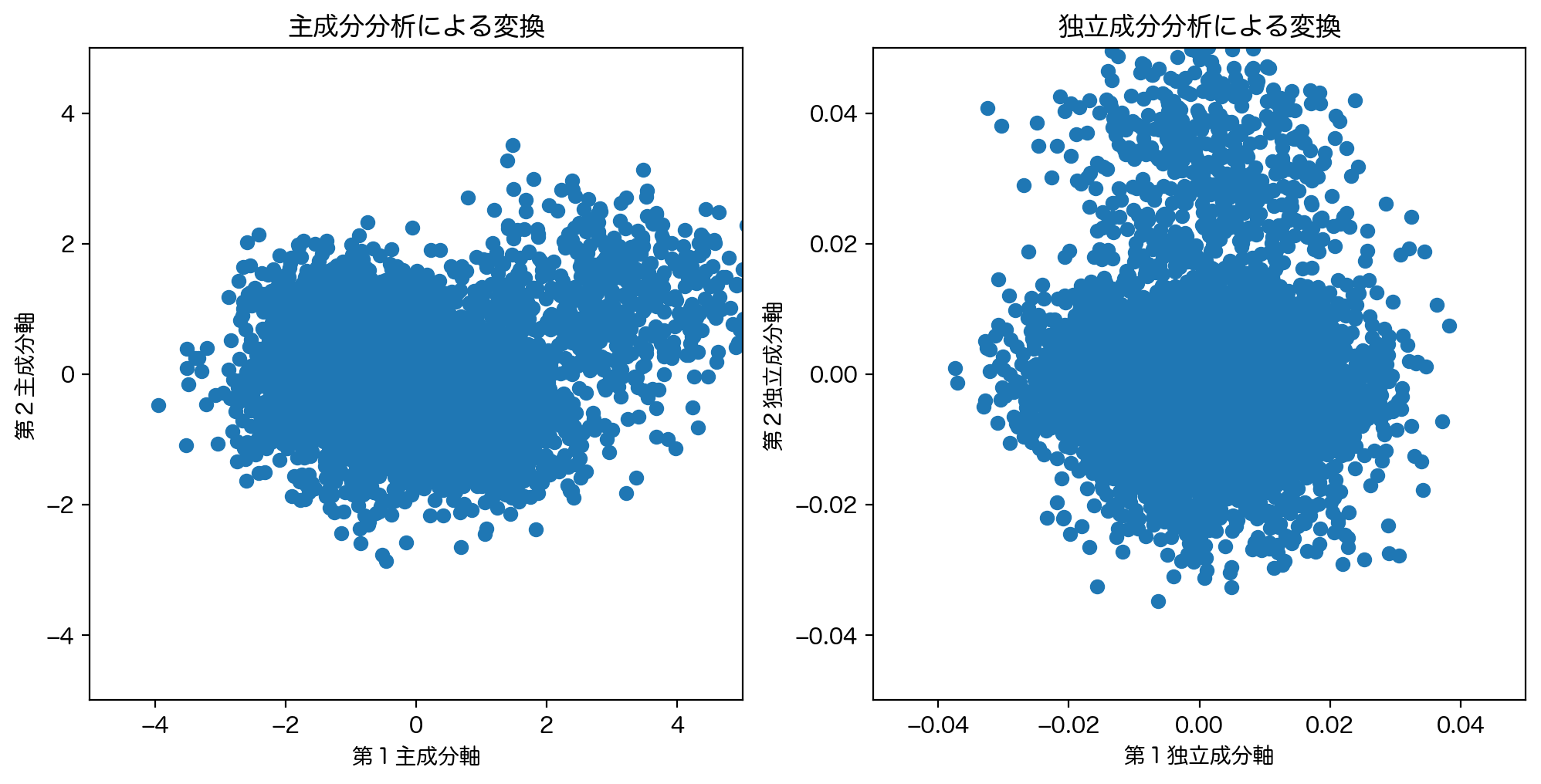
主成分分析は最も分散の大きな方へ第1主成分軸をとり、第2主成分軸以降はそれまでとった主成分軸に直交する空間内で、最も分散の大きな方向をとります。結果として主成分分析では第1主成分軸と第2主成分軸は直交します。逆に考えれば元々の座標系を直交を保ったまま回転するような変換になります。
一方独立成分分析は最も互いに独立な成分方向への変換を行います。このため、元々の座標系に独立成分軸をプロットしたとしても、独立成分軸は必ずしも直交しません。
しかし、独立成分分析で変換した先の座標系は、(多変量正規分布に従っているとの仮定のもと)最も独立な座標系であり、すなわち各データ点がより正方形に近づくような変換となります。
因子分析#
【因子分析(Factor Analysis:FA)とは】
因子分析は主成分分析と同様に説明変数列とは別の変数列を定義して分析し次元圧縮を行う方法です。
因子分析は既存の説明変数 \(X\)を分解して、「共通因子 \(f_j\)」という仮定の新しい変数で構成する次式に変換します。
ここで \(\lambda_{ij}\)は因子負荷量と呼ばれ、得られた共通因子が分析に用いた変数に与える影響の強さを表す値です(統計的には観測変数と因子得点との相関係数に相当する)。また \(e_i\)は独自因子と呼ばれる誤差項です。
因子分析では共通因子の数 \(N\)は解析者が決めます。
主成分分析では分散に着目し、第1主成分が分散が最大となる方向に軸をとった成分で最も寄与率が高くなります。これは次元圧縮を行う際の圧縮次元先が何次元であっても、当然第1主成分それ自体は変わりません。
一方、因子分析の場合は、上式の通り共通因子が説明変数に従属しており、共通因子の数に依って因子負荷量の感度(大きさ)は異なります。すなわち、因子分析では、複数の変数があったとき、その背後にそれらに影響する構成概念があるものと仮定し、少数の潜在的変数で複数の変数間の関係を説明しようとすることを目指します。
今回は共通因子の数は2個として解析を行います。
from sklearn.decomposition import FactorAnalysis
factor = FactorAnalysis(n_components=2)
factor.fit(df)
factor_transform = factor.transform(df)
pd.DataFrame(factor_transform, index = df.index, columns = ["第"+str(d+1)+"因子" for d in range(2)])
| 第1因子 | 第2因子 | |
|---|---|---|
| 2020-04-13 00:00:00 | -0.333573 | -0.477704 |
| 2020-04-13 00:00:10 | -0.403107 | -0.534007 |
| 2020-04-13 00:00:20 | -0.343220 | -0.402952 |
| 2020-04-13 00:00:30 | -0.376103 | -0.410238 |
| 2020-04-13 00:00:40 | -0.347630 | -0.449540 |
| ... | ... | ... |
| 2020-04-13 23:59:20 | 0.006270 | -0.135670 |
| 2020-04-13 23:59:30 | -0.012272 | -0.061538 |
| 2020-04-13 23:59:40 | -0.007303 | -0.109079 |
| 2020-04-13 23:59:50 | -0.015282 | -0.103497 |
| 2020-04-14 00:00:00 | -0.018364 | -0.076024 |
8641 rows × 2 columns
以下の図では因子分析の結果から、2つの共通因子平面に各データ点に対応する変換後データを散布図でプロットしました。
また元の変数が因子分析の結果、それぞれ2つの共有因子に対して元の各変数列がどのように影響を受けているかを確認するために、対応する因子負荷量の大きさと方向を示しました。
import matplotlib.patches as patches
plt.figure(figsize = [8,6], dpi = 200)
plt.axes().set_aspect('equal')
plt.scatter(factor_transform[:,0], factor_transform[:,1])
for n, column in enumerate(df.columns):
plt.annotate('', xy = (0,0), xytext = factor.components_[:,n]*5, xycoords='data', arrowprops=dict(arrowstyle="<-"))
if(np.linalg.norm(factor.components_[:,n]) > 0.7):
plt.text(factor.components_[0,n]*5, factor.components_[1,n]*5, column, fontsize = 5)
theta = np.linspace(0, 2*np.pi, 1000)
for r in range(1, 4):
plt.plot(r*np.cos(theta), r*np.sin(theta), color = 'red')
plt.xlim(-3,3)
plt.ylim(-3,3)
plt.xlabel('第1共通因子')
plt.ylabel('第2共通因子')
plt.title('因子分析による共通因子')
plt.show()
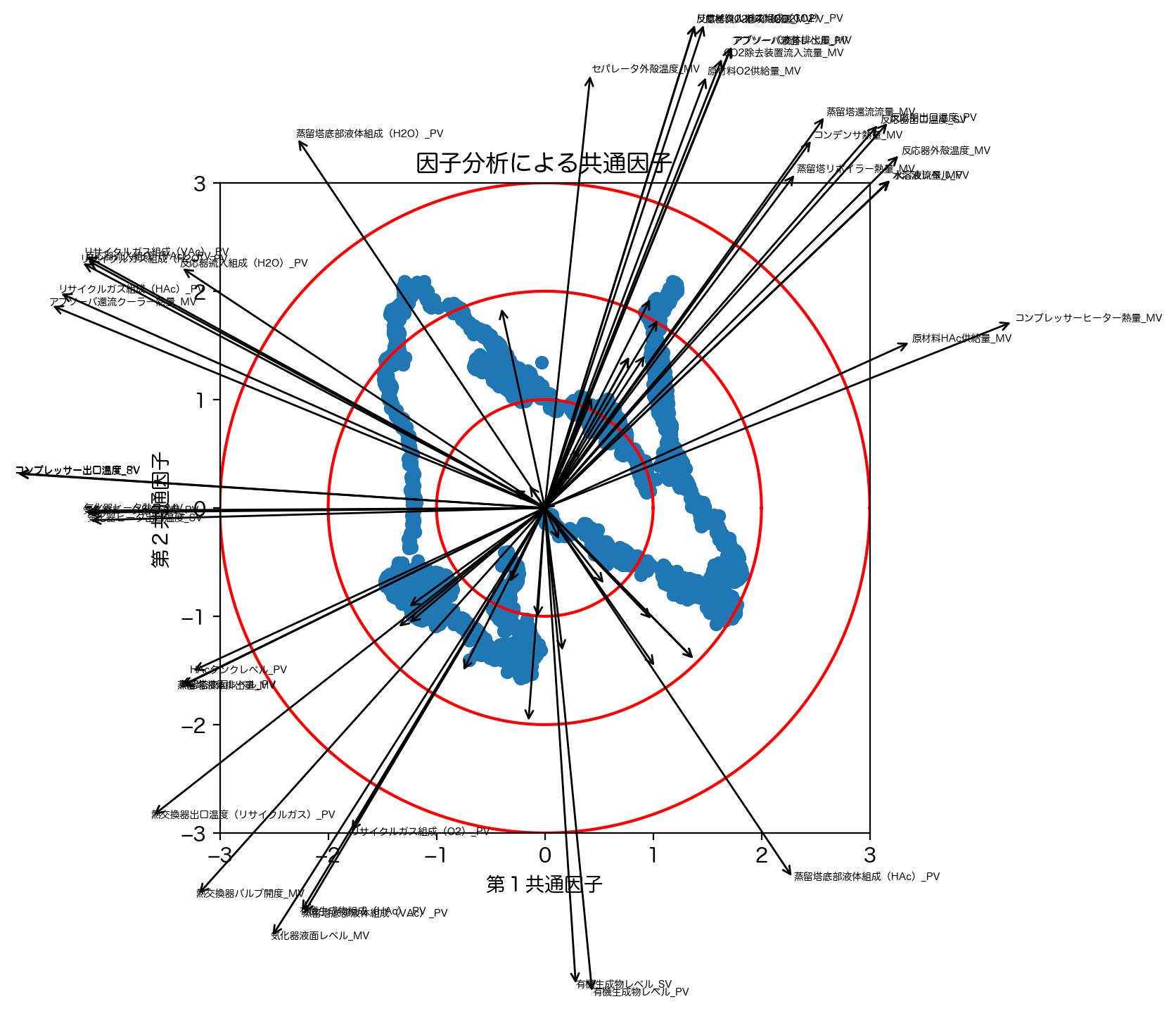
因子分析では何らかの潜在的な共通因子を抽出できますが、この因子が何なのかを簡潔に表現するためには、相応のドメイン知識やノウハウが必要となり、解析者のみでは断定は難しいです。
非負値行列因子分解#
【非負値行列因子分解(Non-negative Matrix Factorization:NMF)とは】
実世界には、パワースペクトル、画素値、頻度、個数など、非負値(すべての値が0または正)で表わされるデータが多く存在します。
主成分分析や独立成分分析などの多変量解析では、所与のデータを複数の加法的な成分に分解することを目的としますが、これらと同様の分解スキームでかつ上述のような非負値のデータから非負値の構成成分を抽出したい場面が多々あります。
【例】
複数の音源の音響信号が混在する多重音のパワースペクトルから個々の音源のパワースペクトルを分離し、雑音除去や音源分離に活用
顔画像データを目や鼻などの顔のパーツに該当する画像データに分解し、顔認証や顔画像合成に活用
文書データ (文書に出現する各単語の個数のデータ) から「時事」や「スポーツ」や「経済」といった潜在的なトピックに該当するような単語ヒストグラムの構成成分を抽出し、各文書に対し自動インデキシングを行う。文書検索に活用。
このように、非負値のデータを加法的な構成成分に分解することを目的とした多変量解析手法を非負値行列因子分解といい,さまざまな分野で近年注目を集めています。
非負値行列因子分解では、すべての要素が非負値の行列 \(X\:(\in\mathbb{R}^{n\times p})\) を、ふたつのすべての要素が非負値の行列 \(W\:(\in\mathbb{R}^{n\times r})\) と \(H\:(\in\mathbb{R}^{r\times p})\) の積で近似します。
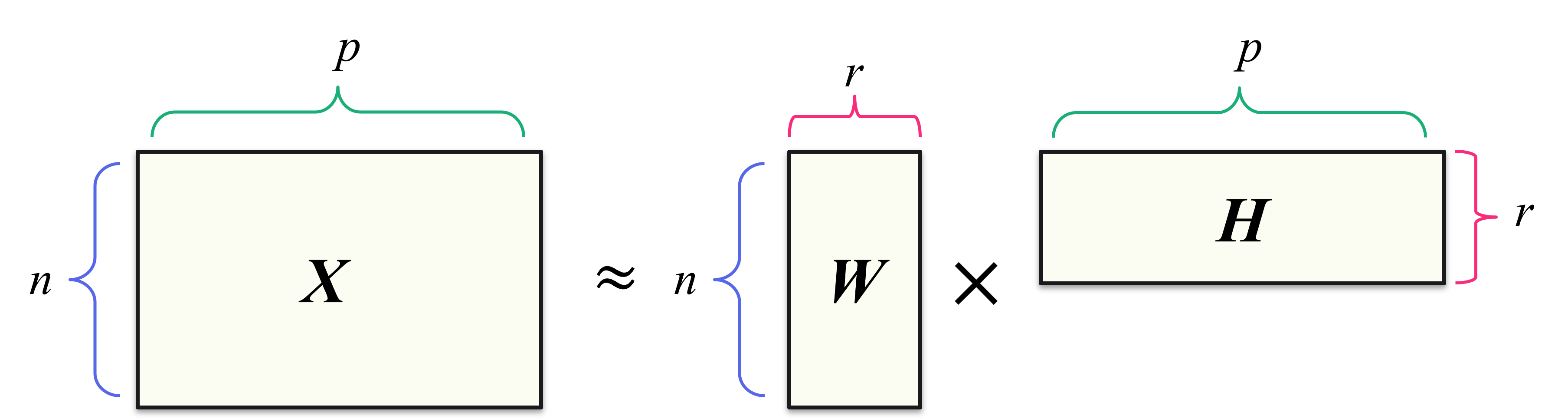
音響信号の分析で現れるパワースペクトルの行列では一般に行の添字 ( \(n\) ) が周波数成分、列の添字 ( \(p\) ) が時刻を表します。このような行列を \(X\) とおいた場合、この分解において \(W\) は各列がひとつの基底ベクトルに相当し、\(H\) はもとの行列 \(X\) をより良く復元できるような最良の基底ベクトルの比率に相当します。一方で、テーブルデータの分析で表れる行列では一般に行の添字が各データ点を、列の添字が特徴量を表すため、音響信号の場合とは逆に \(W\) が基底ベクトルの比率に相当し、 \(H\) の各行がひとつの基底ベクトルに相当することになります。この節では音響信号の分析の慣習に従って議論を進めますが、文献によってはこれらの記号が入れ替わっていることに注意してください。
行列の要素に負値を許すと、\(X\) の復元に際して基底ベクトルを引くことも許容し、これは基底ベクトルをマイナスに積み上げて大きさを減らすと言っているようなもので、上述した非負値データに対しては解釈が難しくなります。
また、基底ベクトル \(W\) と比率 \(H\) を非負に限定することで、係数が疎になりやすくなりさらに解釈性も増す効果もあります。
すなわち、非負値行列因子分解では、比率 \(H\) の意味はその基底ベクトル \(W\) を使うという意味で一貫していて理解しやすく、同時にもとのデータと共通部分が少ないような基底ベクトルは全く使わないという方向になりやすくなります。(言い換えれば、疎にするために各基底ベクトル \(W\) はいくつかのデータの共通部分を抽出したようなものになりやすいとも理解できます)。
ここでは 気化器圧力_PV に注目し、そのスペクトログラムに対して非負値行列因子分解を行ってみます。信号処理に関しての詳細はまたの機会に譲ります。
plt.figure(figsize = [8,6], dpi = 200)
df['気化器圧力_PV'].plot()
plt.title('気化器圧力_PV')
plt.show()
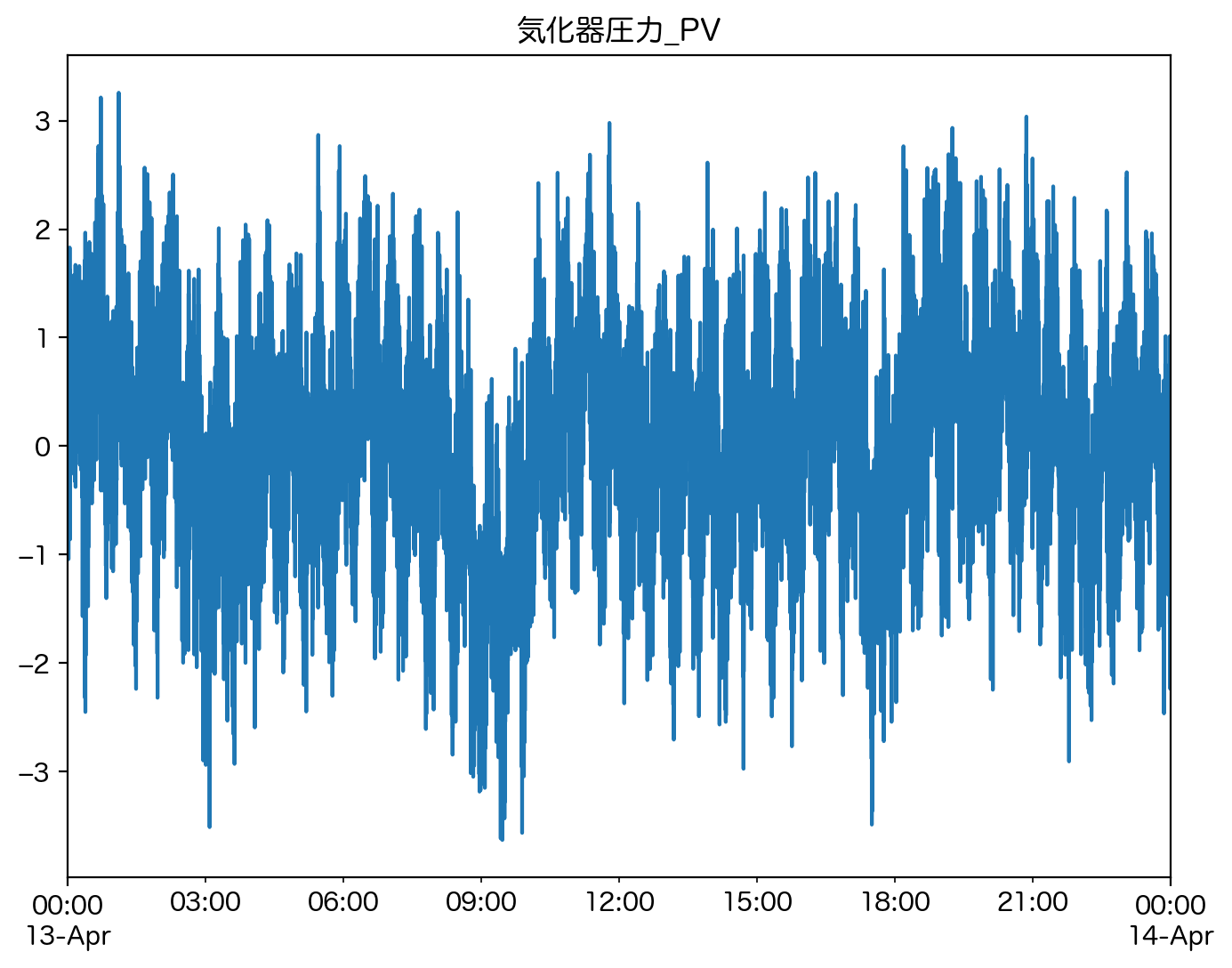
このデータに対してスペクトログラムを計算し時間周波数解析を実行します。
from scipy.signal import spectrogram
# 元々のデータからサンプリングレートを計算
fs = 1/((df.index[-1]-df.index[0])/(len(df) - 1)).total_seconds()
# 周波数、時間、強さが返ってくる
# 強さは絶対値表記する
freq, time, power = spectrogram(df['気化器圧力_PV'], fs, nperseg = 360)
power = np.abs(power)
plt.figure(figsize = [8,6], dpi = 200)
plt.pcolormesh(time, freq, 10 * np.log(power), cmap = 'jet', vmin = -90, vmax = 70)
plt.colorbar()
plt.title('気化器圧力_PV のスペクトログラム [dB]')
plt.xticks([3600 * hour for hour in np.arange(2,24,2)],["06-25 " + str(hour).zfill(2) for hour in np.arange(2,24,2)], rotation = 30)
plt.ylabel('Frequency [Hz]')
plt.show()
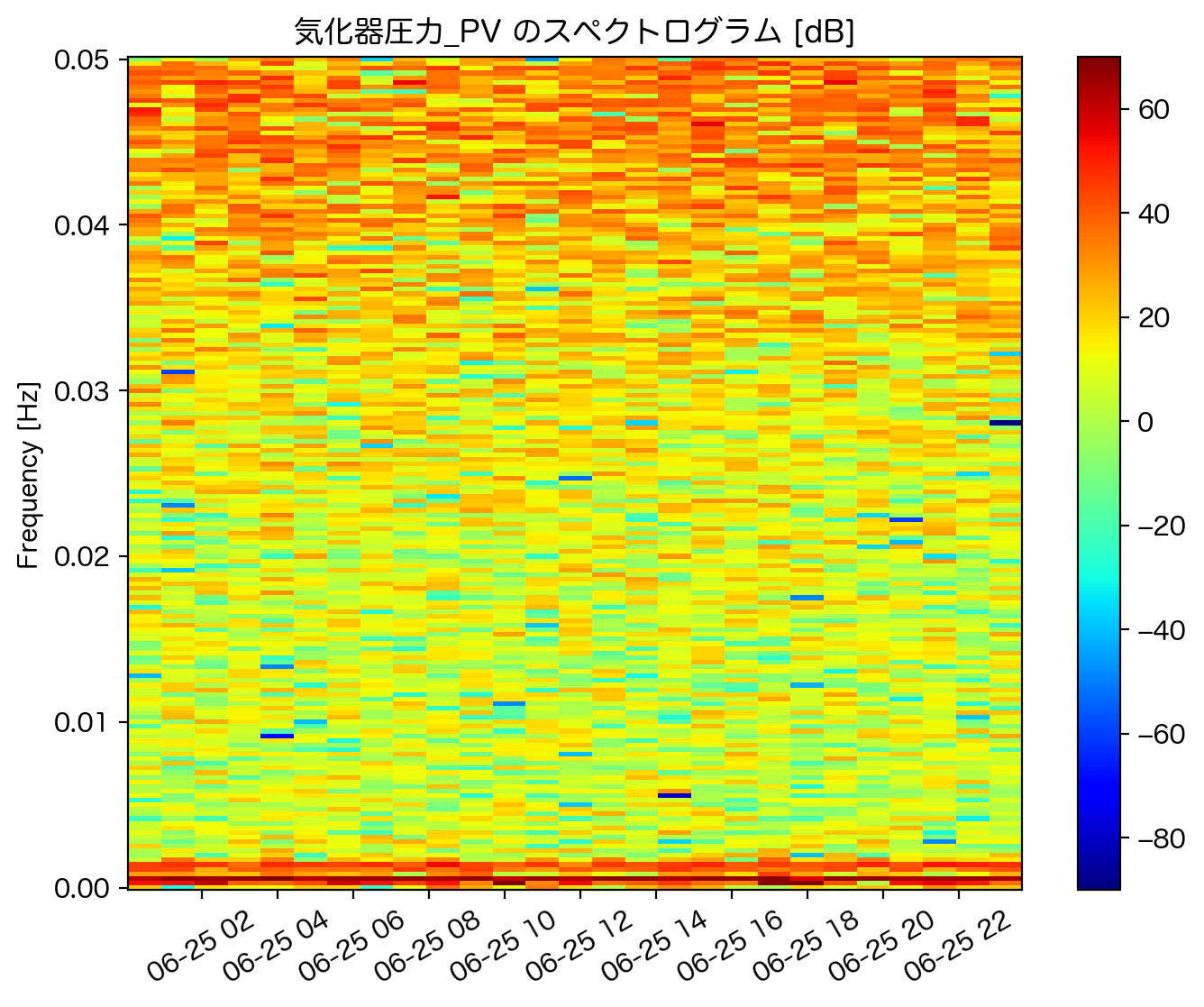
※スペクトログラムはデシベル表記、すなわち対数表記でプロットをしているので負値も取っていることに注意。
このスペクトログラムを非負値行列因子分解を用いて5つの基底に分解してみます。
from sklearn.decomposition import NMF
n_components = 5
nmf = NMF(n_components = n_components)
nmf.fit(power)
#基底ベクトルの行列 Wと、基底ベクトルの比率 Hを得る
W = nmf.transform(power)
H = nmf.components_
import matplotlib.gridspec as gridspec
plt.figure(figsize = [16,12], dpi = 200)
gs = gridspec.GridSpec(n_components * 3, n_components * 3)
for n in range(n_components):
plt.subplot(gs[n_components:, n])
plt.plot(-10 * np.log(W[:-1,n]), np.arange(len(W)-1))
plt.ylim(0, len(W)-1)
plt.xlim(-50, 50)
plt.yticks([len(W)/5*m for m in range(6)], [f'0.0{m}' for m in range(6)])
plt.xticks([-30, 0, 30], [30, 0, -30])
plt.text(-45, len(W)-5, 'base {}'.format(n+1))
if(n != 0):
plt.tick_params(labelleft=False)
for n in range(n_components):
plt.subplot(gs[n, n_components:])
plt.bar(np.arange(len(H.T)-1)+0.5, H.T[:-1,n])
plt.text(24, 18, 'rate {}'.format(n+1))
plt.ylim(0, 25)
plt.xlim(0, len(H.T)-1)
plt.yticks([0, 20], [0, 20])
plt.tick_params(labelbottom=False)
plt.subplot(gs[n_components:, n_components:])
plt.pcolormesh(time, freq, 10 * np.log(W @ H), cmap = 'jet', vmin = -90, vmax = 70)
plt.tick_params(labelleft=False)
plt.xticks([3600 * hour for hour in np.arange(2,24,2)],["06-25 " + str(hour).zfill(2) for hour in np.arange(2,24,2)], rotation = 30)
plt.show()
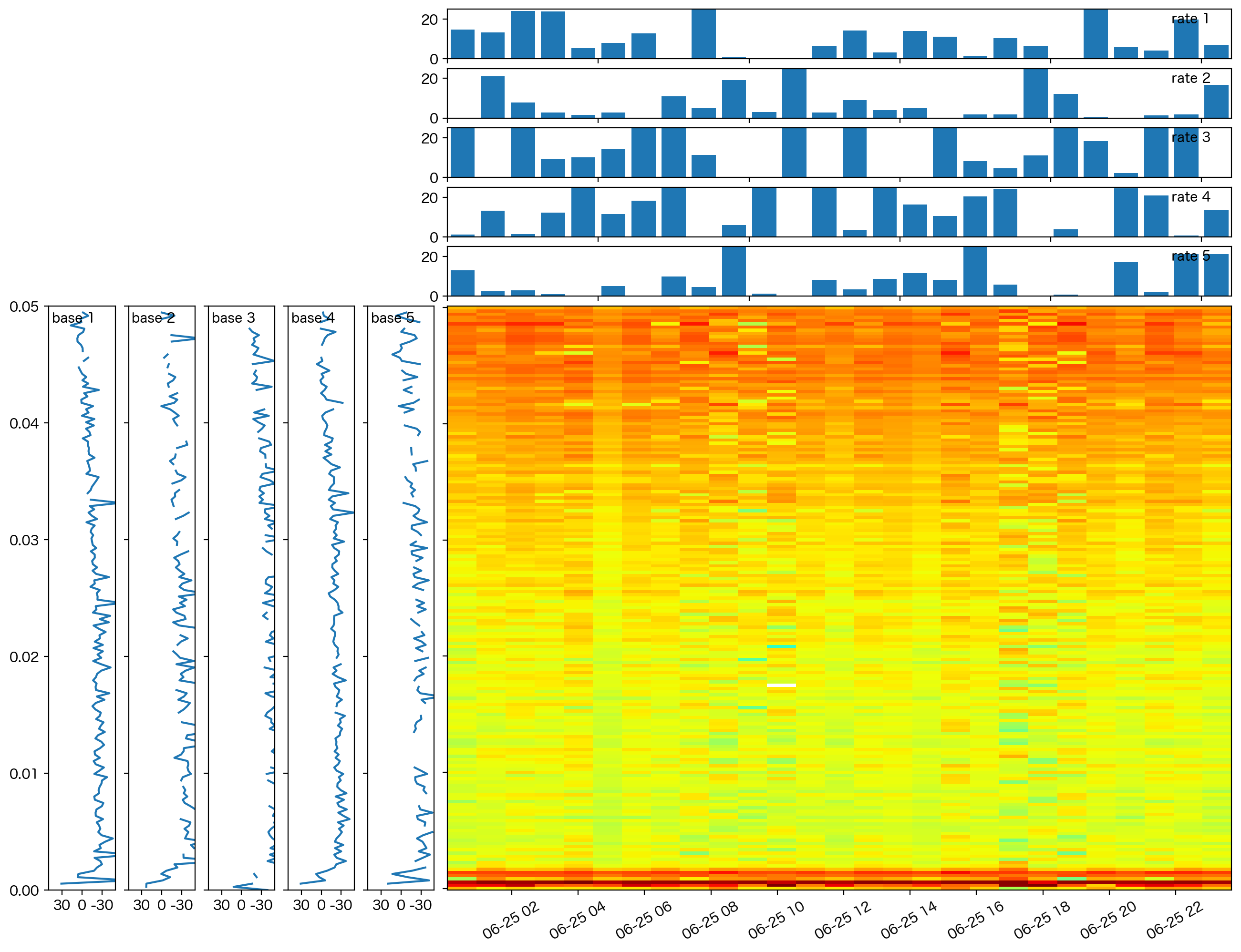
この図では基底の数が5個 (\(k\in\{1,2,3,4,5\}\)) で分解した場合で、base k は\(W\)のうち\(k\)番目の基底スペクトルを、rate k は\(H\)のうち時刻ごとの各基底スペクトル\(k\)のアクティビティを示しています。
特に base k は、この系列データに頻出するスペクトルパーツが獲得されていると考えることができます。
※この図では、対数化前のパワーについて非負値行列因子分解を行い、その後スケーリングのために個々の基底においても対数を取っていることに注意。なお値の不連続点はパワー0.0、すなわち \(\log(0.0)\) による。
またヒートマップは、この分解された基底スペクトルとアクティビティから復元された行列、すなわち低ランクスペクトログラムを表現しています。
小括#
本項では前後編に渡って次元圧縮の手法をまとめました。
次元圧縮の目的は、データの本質的な性質を可能な限り残して、より解析しやすい低次元空間に変換することです。いずれの手法においても、では何次元空間に移せば良いのかということは非常に重要な課題であり、次元圧縮の効能が情報損失による影響を下回ってしまうと元も子もありません。
本項はあくまでも単なる方法論であることを強く意識し、ドメイン知識や系のダイナミクス(因果グラフなど)を駆使してケース・バイ・ケースで対処することが重要です。
※冒頭でも述べたように本項では「次元圧縮」についての記事です。「次元削減」の方の記事も併せて参照ください。
参考文献#
前処理大全 第8章 数値型 8-6 主成分分析による次元圧縮
パターン認識と機械学習(下) 第12章 連続潜在変数

