ベイズ最適化によるハイパーパラメータ最適化

ベイズ最適化によるハイパーパラメータ最適化#

本稿では、「ハイパーパラメータ探索の基本的な手法」でのハイパーパラメータおよびその探索に関する基本的な解説を前提に、ガウス過程を用いたベイズ最適化 (Bayesian optimization, BO) によるハイパーパラメータ最適化について解説します。

ハイパーパラメータ最適化#

機械学習におけるハイパーパラメータ探索の問題は、対応するハイパーパラメータの空間上での最適化問題と見なすことができます。いま、所与の訓練データ \(D\) を用いて学習することを考え、そのプロセスにおいて指定すべきハイパーパラメータ \(x \in \mathcal{X}\) を、対応する適当な指標 \(y = f ( x ) \in \mathbf{R}\) が最小になるよう選択したいものとします。

例えば、訓練データ \(D\) として \(n\) 変量（ \(n = 10\) とします）の回帰問題に対応するものが与えられて、

  • 入力変数を主成分分析 (PCA) に基づいて \(p\) 次元に削減

  • 出力変数を平均0, 分散1に標準化

  • Ridge回帰のモデルを正則化項の乗数 \(\lambda\) として当てはめ、重みを推定

というパイプラインで解析するものとします。このパイプラインのハイパーパラメータとしては

  • PCAに基づいて削減した入力の次元数 \(p \in \{ 1, \ldots, 9 \} \subset \mathbf{Z}\)

  • Ridge回帰における正則化項の乗数 \(\lambda \in [0.0001, 1] \subset \mathbf{R}\)

の2つを探索するものとして、 \(x = ( p, \lambda ) \in \{ 1, \ldots, 9 \} \times [0.0001, 1] = \mathcal{X}\) とおきます。いま、訓練データで（データの順序をシャッフルしない）3-foldの交差検証 (CV) を行った際の平均二乗誤差 (MSE) の平均を \(y\) とおき、この \(y\) が最小になるハイパーパラメータを探索したいものとします。

このとき、ハイパーパラメータ \(x = ( p, \lambda )\) が決まると対応するCV損失 \(y\) の値も決まるので、この関係を関数 \(f: \mathcal{X} \to \mathbf{R}\) を使って \(y = f ( x )\) と表すことにします。CV損失 \(y\) を最小にするハイパーパラメータ \(x\) を探索することは、目的関数 \(f ( x )\) の \(x \in \mathcal{X}\) 上での最小化問題を解くことに対応します。

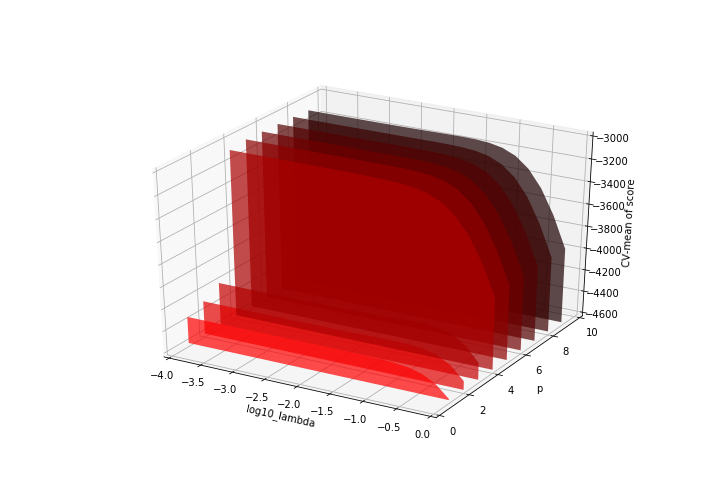
ImageOfLossSurface

（図はこの関数 \(f ( x ) = f ( p, \lambda )\) の概形。2変数関数だが \(p\) は整数値しか取らないことに注意。 \(\lambda\) については常用対数 \(\log_{10} \lambda\) のスケールとしている）

import numpy as np
from sklearn.base import clone
from sklearn.datasets import load_diabetes
from sklearn.decomposition import PCA
from sklearn.linear_model import Ridge
from sklearn.model_selection import cross_validate
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler

feature, target = load_diabetes(return_X_y=True)  # 糖尿病データセットを利用
feature_train, target_train = feature[:300], target[:300]  # 訓練データ
feature_test, target_test = feature[300:], target[300:]  # 試験データ

base_pipeline = Pipeline(
    steps=[
        ("pca", PCA()),  # ここではパラメータを何も設定しない
        ("ridge", Ridge()),
    ]
)


def convert_to_params(x):
    # x: shape=(2,), dtypes=np.floatingのnp.ndarray
    return x[0].astype(np.integer), x[1].astype(np.floating)


def f(x):
    pca__n_components, ridge__alpha = convert_to_params(x)
    params = {
        "pca__n_components": pca__n_components,
        "ridge__alpha": ridge__alpha,
    }

    cloned_estimator = clone(base_pipeline)  # estimator（ここではpipeline）を複製する
    cloned_estimator.set_params(**params)
    scores = cross_validate(
        estimator=cloned_estimator,
        X=feature_train,
        y=target_train,
        cv=3,  # 3-fold CVで評価
        scoring="neg_mean_squared_error",
    )
    return scores["test_score"].mean()  # スコアのCV平均のみを返す

x = np.array([3, 0.001])
f(x)

-4213.298591621135

PCAやRidge回帰ではそれぞれ最適な重みを決定的に求めることができるため、目的関数 \(f\) の正しい値を直接得ることができます。しかし、例えば深層学習のモデルの重みを確率的勾配降下法 (SGD) で求める場合にはパラメータの初期値の生成、勾配を計算するミニバッチの抽出などにランダム性があるため、実際に得られる \(f\) の値も雑音を含むものになります。このため、一般には最適化問題

\[\begin{split} \begin{align} \text{minimize} \quad & f ( x ) \\ \text{subject to} \quad & x \in \mathcal{X} \end{align} \end{split}\]

を解くために、各 \(x_i\) ( \(i = 1, 2, \ldots)\) に対して雑音 \(\epsilon_i\) の乗った観測

\[ y_i = f ( x_i ) + \epsilon_i \]

が逐次的に得られ、しかも各 \(( x_i, y_i )\) の組のみが利用できるといったような設定を考えます。

このような問題設定の下で、最適化問題の手法を利用したハイパーパラメータの探索をハイパーパラメータ最適化 (hyperparameter optimization, HPO) と呼びます。HPOの目的関数 \(f\) は所与のハイパーパラメータで学習したモデルの誤差（CV誤差など）とする場合が多いのですが、それゆえ

  • ハイパーパラメータ \(x\) の属する空間がしばしば極めて高次元

  • 新しいハイパーパラメータ \(x\) に対する \(f( x )\) の評価にしばしば多大な時間・計算コストがかかる

    • \(f ( x )\) を評価するたびにモデルの学習を（CVなら何回も）行う必要がある

  • 関数 \(f\) の大域的な性質は自明でない

  • 勾配 \(\nabla f ( x )\) の計算は一般に不可能

などの特徴があります。このため、grid searchを筆頭とする力任せの手法はしばしば非現実的な時間を要することになり、特に高次元の場合は全く適用できません。また、勾配降下法に代表される、目的関数の勾配の情報を利用する局所最適化の手法も利用できません。

HPOでしばしば用いられる手法には次のようなものがあります：

これらの手法はいずれも関数 \(f\) 自身の形状を不問として、入出力の組 \(( x_i, f ( x_i ) )\) 以上の情報を利用しません。その意味において、これらの手法はブラックボックス最適化 (black-box optimization) とも呼ばれます。

本項では、このうちsequential model-based optimization (SMBO) と呼ばれる手法からガウス過程によるベイズ最適化 (Bayesian optimization) を用いた方法について簡単に解説します。また、この手法をscikit-learnのハイパーパラメータ探索に利用する場合の実装例についても紹介します。

Sequential Model-Based Global Optimization#

Sequential model-based global optimization (SMBO) とは、次のような形式で記述できる最適化アルゴリズムのことを指します：

ImageOfSMBO

（図は [Bergstra et al., 2011] より引用）

ここで \(\mathcal{H}\) は観測の履歴 (history) で、これまでに評価した入出力の組 \(( x_i, f ( x_i ) )\) たち（実際には雑音を含んだ \(( x_i, y_i )\) たち）を格納しています。各 \(M_t\) は関数 \(f\) のモデルで、例えばガウス過程やTPEなどが用いられます。写像 \(S\) は、最適化の難しい目的関数 \(f\) の代理として一般的な手法で最適化できる関数 \(S ( \cdot, M )\) を提供するためのものです。このため \(M_t\) やその族をサロゲートモデル (surrogate model; 代理モデル) と呼んだり、関数 \(S ( \cdot, M )\) やその族をサロゲート関数 (surrogate function; 代理関数) と呼んだりします。

サロゲート関数として利用される典型的な指標に 期待改善量 (expected improvement; EI) があります。モデル \(M\) の下で関数 \(f: x \mapsto y\) が定める条件付き確率密度関数を \(p_M ( y | x )\) と書いたとき、適当な閾値 \(y^*\) に対するEIは

\[ \mathrm{EI}_{y^*} ( x ) = \int_{- \infty}^\infty \max ( y^* - y, 0 ) p_M ( y | x ) d y \]

で計算されます。被積分項の \(\max ( y^* - y, 0 )\) は新しい値 \(y\) が現在の基準値 \(y^*\) をどれほど（値が小さくなる方向に）改善するかを表した量で、定義より非負値を取ります。従って、EIはモデル \(M\) の下で各 \(x\) を評価したときの値が平均的に現在の規準値 \(y^*\) をどれほど改善するかを表す指標となり、これを最大にする \(x\) を評価すれば現在の基準値 \(y^*\) 最も大きく改善することが期待されます。

EIをSMBOのサロゲート関数として利用する場合は形式的に反数を取って \(S ( x, M ) = - \mathrm{EI}_{y^*} ( x )\) としますが、いずれにせよ \(M\) をガウス過程やTPEにした場合は容易にEIを計算でき、また最適化できます。この閾値 \(y^*\) にループの各時点 \(t\) での履歴 \(\mathcal{H}\) の中での最良の値

\[ y^* = \min_{( x, y ) \in \mathcal{H}} y \]

を代入していくことで、この最良の値 \(y^*\) を最も大きく改善しそうな候補 \(x\) を逐次的に選択、評価していくのが（サロゲート関数としてEIを利用した場合の）SMBOです。

ガウス過程によるベイズ最適化#

ベイズ最適化 (Bayesian optimization; BO) はブラックボックス最適化の一種で、目的関数 \(f\) を確率的にモデリングした上でベイズ統計の方法を利用して最適解の探索とモデルの更新を逐次的に進めていくものを指します。典型的には目的関数 \(f\) の事前分布に適当な確率過程を設定して、新しい \(( x_i, y_i )\) の組が得られるごとに \(f\) の事後分布を更新します。この更新した事後分布（または対応する予測分布）を用いたサロゲート関数を最適化することで次に探索する入力 \(x_{i + 1}\) を決定し、実際に \(f ( x_{i + 1} )\) を評価して対応する \(y_{i + 1}\) を得ることでループを繰り返します。

関数 \(f : \mathcal{X} \to \mathbf{R}\) の事前分布としてはガウス過程 (Gaussian process; GP) がよく利用されます（ガウス過程についての詳細な解説は別項を参照）。いま、関数 \(f\) が平均関数 \(\mu : \mathcal{X} \to \mathbf{R}\) およびカーネル関数 \(K : \mathcal{X} \times \mathcal{X} \to \mathbf{R}\) のガウス過程 \(\mathrm{GP} ( \mu, K )\) に従うものとし、これに独立同分布な雑音 \(\epsilon_i \sim \mathrm{N} ( 0, \alpha )\) を加えた回帰モデル \(y_i = f ( x_i ) + \epsilon_i\) を考えます。これまでに \(\mathcal{H} = \{ ( x_1, y_1 ), \ldots, ( x_n, y_n ) \}\) が観測されているものとします。このとき

\[\begin{split} \mu ( X ) = \left[ \begin{array}{c} \mu ( x_1 ) \\ \vdots \\ \mu ( x_n ) \end{array} \right], \quad K ( X, X ) = \left[ \begin{array}{ccc} K ( x_1, x_1 ) & \cdots & K ( x_1, x_n ) \\ \vdots & \ddots & \vdots \\ K ( x_n, x_1 ) & \cdots & K ( x_n, x_n ) \end{array} \right], \quad \mathbf{y} = \left[ \begin{array}{c} y_1 \\ \vdots \\ y_n \end{array} \right] \end{split}\]

とおくと、新しい入力 \(x_* \in \mathcal{X}\) に対する雑音のない出力 \(f_* = f ( x_* )\) の予測分布は

\[\begin{split} K ( X, x_* ) = \left[ \begin{array}{c} K ( x_1, x_* ) \\ \vdots \\ K ( x_n, x_* ) \end{array} \right] \end{split}\]

とおいて

\[\begin{split} f_* | x_*, \mathcal{H} \sim \mathrm{N} ( \mu_* ( \mathcal{H} ) , \sigma_*^2 ( \mathcal{H} ) ) \text{,} \\ \begin{array}{ll} \text{where} & \mu_* ( \mathcal{H} ) = \mu ( x_* ) + K ( X, x_* )^\mathrm{T} K ( X, X ) ( \mathbf{y} - \mu ( X ) ) \text{,} \\ & \sigma_*^2 ( \mathcal{H} ) = K ( x_*, x_* ) - K ( X, x_* )^\mathrm{T} ( K ( X, X ) + \alpha I_n )^{- 1} K ( X, x_* ) \end{array} \end{split}\]

で与えられます。

ベイズ最適化の文脈では、次の探索点を決めるために最大化するサロゲート関数のことを__獲得関数__ (acquisiton function) と呼びます。典型的なサロゲート関数は上述したEIで、 \(f\) の事前分布にガウス過程を設定した場合は

\[ \mathrm{EI}_{y^*} ( x_* ) = \sigma_* ( \mathcal{H} ) \left( \frac{y^* - \mu_* ( \mathcal{H} )}{\sigma_* ( \mathcal{H} )} \Phi ( \frac{y^* - \mu_* ( \mathcal{H} )}{\sigma_* ( \mathcal{H} )}) + \phi ( \frac{y^* - \mu_* ( \mathcal{H} )}{\sigma_* ( \mathcal{H} )}) \right) \]

と書けます。ただし標準正規分布の確率密度関数を \(\phi\) と、また累積分布関数を \(\Phi\) とおきました。この \(\mathrm{EI}_{y^*} ( x_* )\) は \(x_*\) についての勾配も計算でき、一般的な最適化手法で容易に最大化できます。

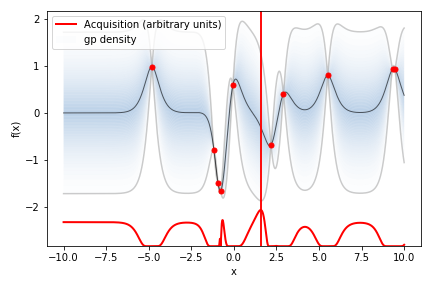
ImageOfGPEIAcquisition

（図は一変数関数の場合のガウス過程によるベイズ最適化（最小化）の一例。グラフ上部の赤点はこれまでに観測された \(( x_i, y_i )\) の組。黒線は事後分布の平均関数 \(\mu_* ( \mathcal{H} )\) で、それを囲う青のグラデーショの領域は \(\mu_* ( \mathcal{H} ) \pm 1.96 \sigma_* ( \mathcal{H} )\) で挟まれた近似の95％確信区間。グラフ下部の赤横線は獲得関数 \(\mathrm{EI}_{y^*} ( x_* )\) の概形で、これを最大化する赤縦線の \(x_*\) で \(f\) の次の評価をする）

ハイパーパラメータ最適化への応用#

ガウス過程によるベイズ最適化を用いてハイパーパラメータ最適化を行う上では、いくつか広く利用されているテクニックや実用上の注意点があります。

入力変数のスケーリング#

ガウス過程のカーネル関数としては、 RBFカーネル (指数二次カーネルとも)

\[ K ( x, x' ) = \exp \left( - \frac{\| x - x' \|_2^2}{2 \ell^2} \right) \]

をはじめ多様なものが用いられますが、そのほとんどは各入力変数のスケールや変数間でのスケールの違いに敏感です（詳細は入力変数のスケーリングの選択を参照）。このため、実用上はしばしばカーネル関数の計算をする前に各ハイパーパラメータの探索範囲が単位区間 \([0, 1]\) に収まるように前処理が行われます。

出力変数のスケーリング#

ガウス過程によるベイズ最適化を行う場合、実用上は出力変数の値 \(y_i\) についてもループの各ステップで

\[ m^{( n )} = \sum_{i = 1}^n y_i, \quad v^{( n )} = \frac{1}{n} \sum_{i = 1}^n \left( y_i - m^{( n )} \right)^2, \quad \tilde{y}_i^{( n )} = \frac{y_i - m^{( n )}}{\sqrt{v^{( n )}}} \]

と改めて平均0、分散1となるよう標準化を行った上で、事前の平均関数として零関数

\[ \mu ( x ) \equiv 0 \]

を設定した \(\mathrm{GP} ( 0, K )\) と \(n\) 個の観測 \(( x_1, \tilde{y}_1^{( n )} ), \ldots, ( x_n, \tilde{y}_n^{( n )} )\) からそのステップでの獲得関数を求めることがよく行われます。これは目的関数 \(f\) が極端に大きいか小さい値をとった場合に事後の平均関数

\[ \mu ( x | \mathcal{H} ) = \mu ( x ) + K ( X, x )^\mathrm{T} K ( X, X ) ( \mathbf{y} - \mu ( X ) ) \]

が履歴に追従できなくなり、最適化に失敗することを防ぐためのものです。

ガウス過程とベイズ最適化のハイパーパラメータに関する処理#

以上の説明から明らかなように、目的関数 \(f\) をモデリングするガウス過程、あるいはそれを用いたベイズ最適化の手続きの中にも複数のハイパーパラメータが存在します。ガウス過程のハイパーパラメータとしては主にカーネル関数のパラメータ (例えば上述のRBFカーネルなら \(\ell > 0\) ) やカーネル関数の選択・構成そのものがあり、ベイズ最適化の手続きのハイパーパラメータとしては入力変数のスケーリング方法や獲得関数の選択があります。

カーネル関数のパラメータについては、階層モデリングの観点からスライスサンプリングを利用して周辺化する方法があります [Murray et al., 2010] [Snoek et al., 2012] 。また入力変数のスケーリングについても \([0, 1] \to [0, 1]\) なるパラメトリックな非線形関数により変換した上で、その非線型関数のパラメータをやはりスライスサンプリングで周辺化するinput warping [Snoek et al., 2014] という手法が提案されています。獲得関数の選択については人間の選択によることが多く、EI以外にも信頼上限 (upper confidence bound; UCB) というものがよく使われます。

履歴の初期化#

実際にSMBOによってHPOを実行する際、多くの場合は [Bergstra et al., 2012] のFigure 1に示されたようなループを回す前に履歴 \(\mathcal{H}\) の初期化が必要になります。関数 \(f\) のモデルにガウス過程を設定してベイズ最適化を行う場合も、空の履歴 \(\mathcal{H} = \emptyset\) における（事前分布から求めた）獲得関数はしばしば \(x_*\) に依存しない定数となります。これでは獲得関数を利用して最適化する意味がありません。

ガウス過程によるベイズ最適化の場合、関数入力 \(x\) の属する空間 \(\mathcal{X}\) が \(k\) 次元Euclid空間 \(\mathbf{R}^k\) の一部と見なせるのであれば、少なくとも（線形独立な） \(( k + 1 )\) 点 \(x_1, \ldots, x_{k + 1}\) における関数 \(f\) の評価結果 \(\{ ( x_1, y_1 ), \ldots, ( x_{k + 1}, y_{k + 1} ) \}\) を予め用意しておき、これを最初の履歴 \(\mathcal{H}\) としてSMBOのループを回すことが推奨されます。履歴を初期化する点列の選び方としては

  • ランダムサンプリング

  • ラテン方格による実験計画

  • Sobol列からの生成

などが利用されます。

Scikit-Optimizeでの実装#

Pythonでガウス過程によるベイズ最適化を実装しているライブラリとしては spearmint や GPyOpt なども有名ですが、本節では Scikit-Optimize ( skopt ) を利用したハイパーパラメータ探索の実装例について解説します。

Scikit-OptimizeはいくつかのSMBOの手法を実装したライブラリで、ガウス過程によるベイズ最適化はその関数 gp_minimize() で、交差検証を伴うハイパーパラメータ探索はクラス BayesSearchCV でそれぞれ利用可能です。この BayesSearchCV はscikit-learnにおける基本的なハイパーパラメータ探索のクラスである GridSearchCV や RandomizedSearchCV と同様の方法で利用できます。

Scikit-optimizeのベイズ最適化において、ガウス過程回帰のカーネルには Matérn 5/2カーネル を定数倍して白色雑音を載せたもの

\[ K ( x, x' ) = C \exp \left( 1 + \sqrt{5} \gamma \frac{\| x - x' \|}{\ell} + \frac{5}{3} \gamma^2 \frac{\| x - x' \|^2}{\ell^2} \right) \exp \left( - \sqrt{5} \gamma \frac{\| x - x' \|}{\ell} \right) + \sigma_\epsilon^2 1_{x = x'} \]

が利用されます。これは連続値を入力変数とするガウス過程回帰で標準的に使用される物の1つです。カーネルのハイパーパラメータである \(C, \ell, \sigma_\epsilon^2\) については周辺対数尤度の最大化によって推定されます。

from skopt import BayesSearchCV
from skopt.callbacks import VerboseCallback, DeltaXStopper
from skopt.space import Real, Integer

# base_pipeline = Pipeline(
#     steps=[
#         ('pca', PCA()),  # ここではパラメータを何も設定しない
#         ('ridge', Ridge()),
#     ]
# )

search_spaces = {
    "pca__n_components": Integer(  # 整数値のパラメータ
        1,
        9,  # 上側についてもinclusive; このパラメータは値1, ..., 9を取る
        transform="normalize",  # ガウス過程回帰の入力変数としては[0, 1]に正規化
    ),
    "ridge__alpha": Real(  # 実数値のパラメータ
        0.0001,
        1.0,
        prior="log-uniform",  # 初期化で対数一様分布からサンプリングし、ガウス過程回帰の入力変数としては対数変換
        transform="normalize",  # （対数変換した上で、さらに）ガウス過程回帰の入力変数としては[0, 1]に正規化
    ),
}
bscv_pipeline = BayesSearchCV(
    estimator=base_pipeline,
    search_spaces=search_spaces,
    n_iter=10,  # 10個のサンプルを評価
    optimizer_kwargs={  # 内部で `skopt.Optmizer` に渡されるキーワード引数の辞書
        # 'base_estimator': 'gp',  # （デフォルトで）ガウス過程によるベイズ最適化を実行する
        "n_initial_points": 5,  # 最初の5点をrandom searchにより初期化する; デフォルトは10
        "acq_func": "EI",  # 獲得関数にEIを指定する
    },
    scoring="neg_mean_squared_error",  # CVのスコアに負のMSEを指定する
    cv=3,  # 3-fold CVで評価
)

bscv_pipeline.fit(
    X=feature_train,
    y=target_train,
    callback=[
        VerboseCallback(n_init=5, n_total=10),  # 最適化の進捗状況を表示
        DeltaXStopper(
            delta=1e-8
        ),  # 直前の点と1e-8より近い点を評価しようとした際に最適化を停止
    ],
)
bscv_pipeline

Iteration No: 1 started. Evaluating function at provided point.
Iteration No: 1 ended. Evaluation done at provided point.
Time taken: 0.0144
Function value obtained: 3109.5882
Current minimum: 3109.5882
Iteration No: 2 started. Evaluating function at provided point.
Iteration No: 2 ended. Evaluation done at provided point.
Time taken: 0.0110
Function value obtained: 3569.8303
Current minimum: 3109.5882
Iteration No: 3 started. Evaluating function at provided point.
Iteration No: 3 ended. Evaluation done at provided point.
Time taken: 0.0101
Function value obtained: 3098.9730
Current minimum: 3098.9730
Iteration No: 4 started. Evaluating function at provided point.
Iteration No: 4 ended. Evaluation done at provided point.
Time taken: 0.0099
Function value obtained: 4213.6366
Current minimum: 3098.9730
Iteration No: 5 started. Evaluating function at provided point.
Iteration No: 5 ended. Evaluation done at provided point.
Time taken: 0.1348
Function value obtained: 3079.2038
Current minimum: 3079.2038
Iteration No: 6 started. Searching for the next optimal point.
Iteration No: 6 ended. Search finished for the next optimal point.
Time taken: 0.2501
Function value obtained: 3079.2053
Current minimum: 3079.2038
Iteration No: 7 started. Searching for the next optimal point.
Iteration No: 7 ended. Search finished for the next optimal point.
Time taken: 0.3013
Function value obtained: 3079.1963
Current minimum: 3079.1963
Iteration No: 8 started. Searching for the next optimal point.
Iteration No: 8 ended. Search finished for the next optimal point.
Time taken: 0.2802
Function value obtained: 3915.5623
Current minimum: 3079.1963
Iteration No: 9 started. Searching for the next optimal point.
Iteration No: 9 ended. Search finished for the next optimal point.
Time taken: 0.2814
Function value obtained: 3079.2191
Current minimum: 3079.1963
Iteration No: 10 started. Searching for the next optimal point.
Iteration No: 10 ended. Search finished for the next optimal point.
Time taken: 0.3517
Function value obtained: 3079.2272
Current minimum: 3079.1963

BayesSearchCV(cv=3, error_score='raise',
              estimator=Pipeline(memory=None,
                                 steps=[('pca',
                                         PCA(copy=True, iterated_power='auto',
                                             n_components=None,
                                             random_state=None,
                                             svd_solver='auto', tol=0.0,
                                             whiten=False)),
                                        ('ridge',
                                         Ridge(alpha=1.0, copy_X=True,
                                               fit_intercept=True,
                                               max_iter=None, normalize=False,
                                               random_state=None, solver='auto',
                                               tol=0.001))],
                                 verbose=False),
              fit_par...
              optimizer_kwargs={'acq_func': 'EI', 'n_initial_points': 5},
              pre_dispatch='2*n_jobs', random_state=None, refit=True,
              return_train_score=False, scoring='neg_mean_squared_error',
              search_spaces={'pca__n_components': Integer(low=1, high=9, prior='uniform', transform='normalize'),
                             'ridge__alpha': Real(low=0.0001, high=1.0, prior='log-uniform', transform='normalize')},
              verbose=0)

bscv_pipeline.cv_results_  # CVの結果を表示

defaultdict(list,
            {'split0_test_score': [-2854.461952431287,
              -3216.5149656776935,
              -2843.791787605836,
              -3988.432177994014,
              -2867.3236524625695,
              -2867.3135860961665,
              -2867.377130809776,
              -3446.1987797086035,
              -2867.2283383504773,
              -2867.1838314247316],
             'split1_test_score': [-2907.2194553578947,
              -3510.5685463679947,
              -2881.3585509735976,
              -4290.414817650562,
              -2912.750964923616,
              -2912.7432530012093,
              -2912.7922988376104,
              -3896.870541799117,
              -2912.678832438567,
              -2912.6458435166337],
             'split2_test_score': [-3567.083290801539,
              -3982.407427171773,
              -3571.7685430783936,
              -4362.062677391595,
              -3457.5366438749825,
              -3457.558921810834,
              -3457.4193822453926,
              -4403.617677825467,
              -3457.7502488985715,
              -3457.852070465992],
             'mean_test_score': [-3109.5882328635735,
              -3569.830313072487,
              -3098.972960552609,
              -4213.636557678724,
              -3079.2037537537226,
              -3079.2052536360693,
              -3079.1962706309264,
              -3915.562333111063,
              -3079.2191398958716,
              -3079.2272484691193],
             'std_test_score': [324.21405949054656,
              315.46979082850214,
              334.6685550106795,
              161.90761444570535,
              268.16380813473864,
              268.17853173430365,
              268.08602598326013,
              391.08803264283443,
              268.3042889647537,
              268.3707205961978],
             'rank_test_score': [1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
             'mean_fit_time': [0.0013496081034342449,
              0.0012617111206054688,
              0.0011056264241536458,
              0.001096963882446289,
              0.0006901423136393229,
              0.0006855328877766927,
              0.0006886323293050131,
              0.0007519721984863281,
              0.0007134278615315756,
              0.0007357597351074219],
             'std_fit_time': [0.0005681280229628601,
              0.00021885769360779062,
              0.0002529546843642699,
              0.00020792515130303192,
              3.680837639195636e-05,
              3.267426861158456e-05,
              3.349269561665712e-05,
              7.405676629546454e-05,
              6.640498401619982e-05,
              6.150182743492982e-05],
             'mean_score_time': [0.0003719329833984375,
              0.0004589557647705078,
              0.00040268898010253906,
              0.0003780523935953776,
              0.00029015541076660156,
              0.00028705596923828125,
              0.00028967857360839844,
              0.00029842058817545575,
              0.00029532114664713543,
              0.00028888384501139325],
             'std_score_time': [1.66016502267025e-05,
              0.00010973696958836174,
              7.87679082966664e-05,
              4.2160033729063246e-05,
              6.7547255709571135e-06,
              5.1907398836796856e-06,
              5.4263146766381465e-06,
              7.469603308047728e-06,
              1.8104468647885718e-05,
              3.5058252016882547e-06],
             'param_pca__n_components': [4, 5, 4, 3, 6, 6, 6, 6, 6, 6],
             'param_ridge__alpha': [0.030541538480406475,
              0.556736377067103,
              0.00023095675959066976,
              0.0001575189715845865,
              0.004381775004368445,
              0.004339888312312935,
              0.004603455469347129,
              0.9940381303107731,
              0.003983102952395606,
              0.0037953321721399163],
             'params': [{'pca__n_components': 4,
               'ridge__alpha': 0.030541538480406475},
              {'pca__n_components': 5, 'ridge__alpha': 0.556736377067103},
              {'pca__n_components': 4, 'ridge__alpha': 0.00023095675959066976},
              {'pca__n_components': 3, 'ridge__alpha': 0.0001575189715845865},
              {'pca__n_components': 6, 'ridge__alpha': 0.004381775004368445},
              {'pca__n_components': 6, 'ridge__alpha': 0.004339888312312935},
              {'pca__n_components': 6, 'ridge__alpha': 0.004603455469347129},
              {'pca__n_components': 6, 'ridge__alpha': 0.9940381303107731},
              {'pca__n_components': 6, 'ridge__alpha': 0.003983102952395606},
              {'pca__n_components': 6,
               'ridge__alpha': 0.0037953321721399163}]})

print(
    f"Test R2 score: {bscv_pipeline.best_estimator_.score(feature_test, target_test)}."
)

Test R2 score: 0.5038952359174607.

ベイズ最適化によるHPOの実際#

ここではガウス過程を用いたベイズ最適化における諸問題とその具体的な対処について、以前の節（ハイパーパラメータ最適化への応用）で挙げた注意点の詳細も含めて各論として紹介していきます。些末な内容も多いため、必要がなければ小括まで読み飛ばしても構いません。

入力変数のスケーリングの選択#

一般的なベイズ最適化で利用されるカーネル関数の多くは定常かつ等方的です。即ち、 \(x, x' \in \mathbf{R}^d\) として \(K ( x, x' )\) がそのEuclid距離 \(r = \| x - x' \|_2\) の関数で書けるようになっています。ガウス過程のカーネル関数は2点 \(x, x'\) における出力の共分散を与えるものでしたから、これはつまり入力変数の値が何であっても、またどの次元における差であっても、差の大きさが同じであれば（事前分布として）同じ共分散を有すると仮定していることになります。

例えば今回の例で（PCAの次元数を形式的に実数と思って） \(x = ( p, \lambda ) \in \mathbf{R}^2\) を変数変換せずにガウス過程回帰の入力とした場合、（事前分布としては） \(( p, \lambda ) = ( 3, 0.01 )\) でのCV損失と \(( p, \lambda ) = ( 3, 0.02 )\) でのCV損失との相関は \(( p, \lambda ) = ( 3, 0.1 )\) での損失と \(( p, \lambda ) = ( 3, 0.11 )\) での損失との相関と同じだと想定していることになりますし、 \(( p, \lambda ) = ( 3, 0.01 )\) での損失と \(( p, \lambda ) = ( 4, 0.02 )\) での損失との相関は \(( p, \lambda ) = ( 3, 0.01 )\) での損失と \(( p, \lambda ) = ( 3, 1.02 )\) での損失との相関と同じだと想定していることになります。確かにMatérn 5/2カーネルはRBFカーネルと比べて \(r\) を増加させた際の共分散の減衰が速く、より複雑にうねった出力関数を許しやすくなっていますが、実用上はこのような場合だとさすがにうまく行かないことが多くなります。

HPOの観点からは、手動での探索やgrid searchの際に指数的に変化させるハイパーパラメータ（多層パーセプトロンにおける各層のユニット数や学習率など）には対数変換を施すという処方箋がよく行われます。対数変換をしても定常性が想定できない場合はinput warping [Snoek et al., 2014] などが行われますが、高度です。等方性については実行可能領域を単位立方体にして各次元共通の長さスケールパラメータ (length-scale parameter) \(\ell\) を導入する以上のケアが行われないことも多いものの、単一の \(\ell\) の代わりに次元毎の長さスケールパラメータ \(\ell_d\) を用意して \(r / \ell = ( x - x' )^\mathrm{T} ( x - x' )\) の代わりに \(\tilde{r} = ( x - x' )^\mathrm{T} ( \mathrm{diag} ( \ell_d ) )^{- 1} ( x - x' )\) を用いることもできます。勿論、後者の場合は各 \(\ell_d\) についての最適化やサンプリングが必要になります。

離散値・カテゴリ値を取るハイパーパラメータの取り扱い#

離散値やカテゴリ値を取るハイパーパラメータが含まれる場合は注意が必要です。そうしたパラメータの種類、およびそれぞれの取りうる値が少ない場合はパラメータの値の組み合わせ毎に個別のガウス過程回帰モデルをあてることもできますが、一般に非現実的です。しばしば行われる処方箋は、こうしたハイパーパラメータの値を所定の方法で適当な実数値（の組）に変換し、変換した先のEuclid空間で通常のベイズ最適化を行い、獲得関数を最適化して得た実数値（の組）を対応する所定の方法で元の離散値・カテゴリ値に変換するというものです。

離散値、特に整数値を取るハイパーパラメータでは、その整数値をそのまま実数値と見なしてベイズ最適化を行い、獲得関数から得た値を四捨五入などの方法で最も近い整数値に変換するという方法がよく取られます。実際、上記の実装でも skopt の内部的には \(p \in \{ 1, \ldots, 9 \}\) を一度実数とみなして獲得関数の最適化まで行い、CV損失を評価する際に \(p\) を整数に丸めています。

カテゴリ値を取るハイパーパラメータでは、いわゆるone-hot encodingでそのパラメータをカテゴリ数の次元の実数値に変換することも行われます。例えば多層パーセプトロンにおける各層の活性化関数の種類をReLU, SoftPlus, tanhの中から選ぶ場合、ReLUは \(( 1, 0, 0 )\), SoftPlusは \(( 0, 1, 0 )\), tanhは \(( 0, 1, 0 )\) と3次元の実数に変換して獲得関数の最適化まで行い、やはりCV損失を評価する際にその3次元の値を対応する点が最も近いハイパーパラメータの値に変換したりします。

とはいえ、獲得関数の大きくなる領域が特定の丸められた値の範囲に集中して最適化の反復がすぐに収束してしまったり、カテゴリ値をone-hot encodingした場合は上述の等方性にもとづくスケーリングの問題が発生しやすかったりと、離散値やカテゴリ値のハイパーパラメータが多い場合、ガウス過程回帰を用いたベイズ最適化はHPOの方法としてあまり適切ではありません。ガウス過程によるベイズ最適化は主に連続値のハイパーパラメータが多いときの手法と割り切って、そうでない場合は別項で解説するTPEなどの手法に頼ることも実用上は重要になります。

ハイパーパラメータの空間が複雑な構造を持つ場合のカーネルの構成#

他のハイパーパラメータが特定の値を取るときのみ意味を持つハイパーパラメータを考えることができます。例を挙げると、多層パーセプトロンを用いた学習で中間層の数 \(h \in \{1, 2, 3\}\) と出力側から数えた \(h'\) 番めの隠れ層のユニット数 \(u_1, u_2, u_3\) を最適化することを考えると、 \(u_2\) は \(h = 2, 3\) のときのみ、また \(u_3\) は \(h = 3\) のときのみそれぞれ意味を持つハイパーパラメータになります。これらの値を（対数変換や正規化のみで）そのまま用いてベイズ最適化を行うと、例えば \(h = 1\) のときにも \(u_2\) や \(u_3\) の値によって獲得関数の値が変わり、 \(( h, u_1, u_2, u_3 )\) の組としては違う値でもそこから構成されたネットワークとしては同一のものが提案され、最適解の探索が極めて非効率になる事態がしばしば発生します。

このような条件を反映したカーネルの構成は可能ですが、実装は極めて煩雑です（ [Swersky et al., 2013] などを参照）。やはりガウス過程によるベイズ最適化は主にパラメータ間に複雑な構造や条件が存在しないときの手法と割り切って、そうでない場合は別項で解説するTPEなどの手法に頼ることも実用上は重要になります。

小括#

本稿では、ガウス過程を用いたベイズ最適化によるハイパーパラメータ最適化の方法と、scikit-optimize ( skopt ) によるその実行方法、並びにこの手法にまつわる各種のテクニックや課題について解説しました。

ベイズ最適化はブラックボックス最適化の手法としては汎用性も高く、極めて強力なフレームワークです。とはいえ、HPOに利用する場合には効率のよい探索を実現するためにいくつもの些末なテクニックがあり、またニューラルネットワークの構造探索のようにハイパーパラメータの空間が複雑な構造を持つ場合は実用性のある実装が非常に煩雑になります。一方、そうした状況を回避できる比較的単純なモデルでの探索手法としては優秀ですので、探索すべきハイパーパラメータの数と種類を見極めた上で適切に利用するのがよいと思われます。

参考文献#

目次