多重共線性に対応した回帰モデル

センサーデータの予測などにおいて説明変数の数を増やすと予測精度が向上しやすいことが一般的に知られています。しかし次元削減の記事でも触れたように、通常の最小二乗法による重回帰分析を行う際、説明変数同士の相関係数が高いと回帰係数の予測精度が悪くなる多重共線性の問題が生じます。この問題を解消する一般的な手法として「相関が高いと考えられる説明変数を外す」ことが挙げられますが、同時に予測に必要な説明変数も外してしまう危険性もあります。

本稿では多重共線性がある時系列データに対し、説明変数を外すことなくモデル単体で多重共線性に対応できる回帰モデルについて説明します。

モジュール、データの読み込み

import warnings

warnings.filterwarnings("ignore")

import datetime
import matplotlib as mpl
import matplotlib.pyplot as plt
from matplotlib.dates import DateFormatter
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split

pd.plotting.register_matplotlib_converters()

準備

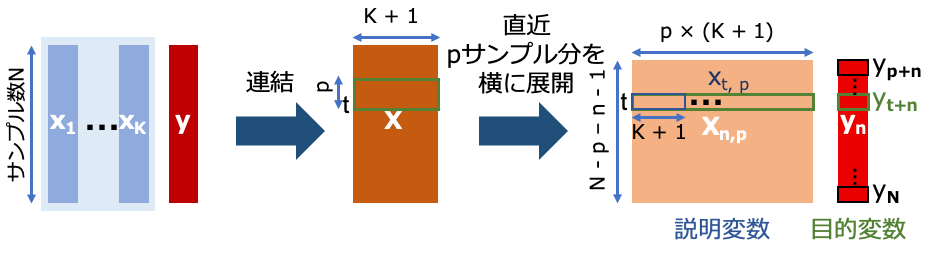
一変量の時系列データ \(\mathbf{y}=(y_1, \ldots, y_N) \in \mathbb{R}^{N}\) を対象に、ある時刻 \(t\) の \(n\) ステップ先の値である \(y_{t + n}\) を目的変数として推測したいとします。
また他の時系列データ \(\mathbf{x}_{k}=(x_1, \ldots, x_N)_{k = 1, \ldots , K} \in \mathbb{R}^{N}\) と \(\mathbf{y}\) を横につなぎ合わせた行列を \(\mathbf{X} \in \mathbb{R}^{N \times (K + 1)}\) としたとき、時刻 \(t\) の直近 \(p\) サンプル分を１ベクトルに引き延ばす処理を \(t = p \sim N - n\) まで繰り返して行列 \(\mathbf{X}_{n,p} \in \mathbb{R}^{(N - p - n + 1)\times (p \times (K + 1)) }\) を作ります。 この \(\mathbf{X}_{n,p} (=\mathbf{x}_{p,p}, \ldots, \mathbf{x}_{t, p}, \ldots, \mathbf{x}_{N - n,p})\) を説明変数として、各サンプルの \(n\) サンプル後の系列 \(\mathbf{y}_{n}=(y_{p + n}, \ldots, y_{N}) \in \mathbb{R}^{N - p - n + 1}\) を目的変数とします。 また \(\mathbf{X}_{n,p}\) と \(\mathbf{y}_{n}\) は正規化済みであるとします。

データの読み込みについて説明します。今回は元データを5秒ごとにサンプリングしたデータを用いて、アブソーバ液面レベル_PVの値を予測することとします。
さらにデータを7:3の比率で学習データとテストデータに分割します。今回用いるような時系列データはデータが連続であるので、学習データがテストデータの各データより未来のデータを含まないように注意します。

df_X = pd.read_csv(
    "../data/2020413.csv", index_col=0, parse_dates=True, encoding="cp932"
).asfreq(
    "5s"
)  # 計算量などの都合で元データを5s間隔でサンプリング
df_y = df_X["アブソーバ液面レベル_PV"]
df_X.head(8)

	気化器圧力_PV	気化器圧力_SV	気化器圧力_MV	気化器液面レベル_PV	気化器液面レベル_SV	気化器液面レベル_MV	気化器温度_PV	気化器ヒータ出口温度_PV	気化器ヒータ出口温度_SV	気化器ヒータ熱量_MV	...	反応器流入組成（CO2）_PV	反応器流入組成（C2H4）_PV	反応器流入組成（C2H6）_PV	反応器流入組成（VAc）_PV	反応器流入組成（H2O）_PV	反応器流入組成（HAc）_PV	セパレータ蒸気排出量_MV (Fixed)	アブソーバスクラブ流量_MV (Fixed)	アブソーバ還流流量_MV (Fixed)	気化器液体流入量_MV (Fixed)
2020-04-13 00:00:00	127.983294	127.883920	18.728267	0.700204	0.7	21876.987772	120.159558	151.274003	150.0	9008.540694	...	0.006273	0.585715	0.214016	0.001370	0.008524	0.109444	16.1026	15.1198	0.766	2.1924
2020-04-13 00:00:05	128.183048	127.934594	18.583280	0.699651	0.7	21927.678085	120.208456	151.242158	150.0	8718.212707	...	0.006256	0.584795	0.214526	0.001373	0.008527	0.109651	16.1026	15.1198	0.766	2.1924
2020-04-13 00:00:10	127.538896	127.931670	18.768258	0.699621	0.7	21852.255542	119.994108	151.364261	150.0	8654.008756	...	0.006301	0.584946	0.213783	0.001376	0.008584	0.110044	16.1026	15.1198	0.756	2.1924
2020-04-13 00:00:15	128.294566	127.955144	18.744669	0.700463	0.7	21854.968904	120.055778	151.114927	150.0	8665.322570	...	0.006283	0.585063	0.214134	0.001378	0.008560	0.109982	16.1026	15.1198	0.756	2.1924
2020-04-13 00:00:20	128.084675	127.798650	18.702331	0.699711	0.7	21883.105458	120.044623	150.942283	150.0	8654.532564	...	0.006262	0.585135	0.213977	0.001372	0.008557	0.109747	16.1026	15.1198	0.756	2.1924
2020-04-13 00:00:25	128.183897	127.927768	18.589676	0.700666	0.7	21869.144563	120.353336	150.945036	150.0	8664.462135	...	0.006264	0.584922	0.213800	0.001374	0.008545	0.109894	16.1026	15.1198	0.756	2.1924
2020-04-13 00:00:30	127.603722	127.878903	18.646610	0.699305	0.7	21894.996658	120.139742	151.004266	150.0	8674.267137	...	0.006275	0.584483	0.213603	0.001382	0.008584	0.110351	16.1026	15.1198	0.766	2.1924
2020-04-13 00:00:35	128.189705	127.980380	18.767198	0.699885	0.7	21823.916443	120.163137	150.987741	150.0	8673.499529	...	0.006255	0.585326	0.213543	0.001370	0.008532	0.110066	16.1026	15.1198	0.756	2.1924

8 rows × 91 columns

# X, yを学習データ、テストデータに分割
X_train, X_test, y_train, y_test = train_test_split(
    df_X, df_y, test_size=0.3, shuffle=False
)
display(X_train.head(8))
display(X_test.head(8))

	気化器圧力_PV	気化器圧力_SV	気化器圧力_MV	気化器液面レベル_PV	気化器液面レベル_SV	気化器液面レベル_MV	気化器温度_PV	気化器ヒータ出口温度_PV	気化器ヒータ出口温度_SV	気化器ヒータ熱量_MV	...	反応器流入組成（CO2）_PV	反応器流入組成（C2H4）_PV	反応器流入組成（C2H6）_PV	反応器流入組成（VAc）_PV	反応器流入組成（H2O）_PV	反応器流入組成（HAc）_PV	セパレータ蒸気排出量_MV (Fixed)	アブソーバスクラブ流量_MV (Fixed)	アブソーバ還流流量_MV (Fixed)	気化器液体流入量_MV (Fixed)
2020-04-13 00:00:00	127.983294	127.883920	18.728267	0.700204	0.7	21876.987772	120.159558	151.274003	150.0	9008.540694	...	0.006273	0.585715	0.214016	0.001370	0.008524	0.109444	16.1026	15.1198	0.766	2.1924
2020-04-13 00:00:05	128.183048	127.934594	18.583280	0.699651	0.7	21927.678085	120.208456	151.242158	150.0	8718.212707	...	0.006256	0.584795	0.214526	0.001373	0.008527	0.109651	16.1026	15.1198	0.766	2.1924
2020-04-13 00:00:10	127.538896	127.931670	18.768258	0.699621	0.7	21852.255542	119.994108	151.364261	150.0	8654.008756	...	0.006301	0.584946	0.213783	0.001376	0.008584	0.110044	16.1026	15.1198	0.756	2.1924
2020-04-13 00:00:15	128.294566	127.955144	18.744669	0.700463	0.7	21854.968904	120.055778	151.114927	150.0	8665.322570	...	0.006283	0.585063	0.214134	0.001378	0.008560	0.109982	16.1026	15.1198	0.756	2.1924
2020-04-13 00:00:20	128.084675	127.798650	18.702331	0.699711	0.7	21883.105458	120.044623	150.942283	150.0	8654.532564	...	0.006262	0.585135	0.213977	0.001372	0.008557	0.109747	16.1026	15.1198	0.756	2.1924
2020-04-13 00:00:25	128.183897	127.927768	18.589676	0.700666	0.7	21869.144563	120.353336	150.945036	150.0	8664.462135	...	0.006264	0.584922	0.213800	0.001374	0.008545	0.109894	16.1026	15.1198	0.756	2.1924
2020-04-13 00:00:30	127.603722	127.878903	18.646610	0.699305	0.7	21894.996658	120.139742	151.004266	150.0	8674.267137	...	0.006275	0.584483	0.213603	0.001382	0.008584	0.110351	16.1026	15.1198	0.766	2.1924
2020-04-13 00:00:35	128.189705	127.980380	18.767198	0.699885	0.7	21823.916443	120.163137	150.987741	150.0	8673.499529	...	0.006255	0.585326	0.213543	0.001370	0.008532	0.110066	16.1026	15.1198	0.756	2.1924

8 rows × 91 columns

	気化器圧力_PV	気化器圧力_SV	気化器圧力_MV	気化器液面レベル_PV	気化器液面レベル_SV	気化器液面レベル_MV	気化器温度_PV	気化器ヒータ出口温度_PV	気化器ヒータ出口温度_SV	気化器ヒータ熱量_MV	...	反応器流入組成（CO2）_PV	反応器流入組成（C2H4）_PV	反応器流入組成（C2H6）_PV	反応器流入組成（VAc）_PV	反応器流入組成（H2O）_PV	反応器流入組成（HAc）_PV	セパレータ蒸気排出量_MV (Fixed)	アブソーバスクラブ流量_MV (Fixed)	アブソーバ還流流量_MV (Fixed)	気化器液体流入量_MV (Fixed)
2020-04-13 16:48:00	128.248067	128.044560	18.624583	0.700518	0.7	20679.607987	120.417161	148.040614	148.17111	8082.837147	...	0.007484	0.579436	0.216502	0.001275	0.008387	0.109208	16.1026	15.1198	0.756	2.1924
2020-04-13 16:48:05	128.339285	127.898364	18.652618	0.700630	0.7	20741.077957	120.180459	147.988304	148.17111	8073.979520	...	0.007463	0.579339	0.216881	0.001269	0.008345	0.109277	16.1026	15.1198	0.766	2.1924
2020-04-13 16:48:10	128.020141	127.954890	18.341206	0.698273	0.7	20780.705482	120.119443	148.032315	148.17111	8069.969436	...	0.007489	0.579036	0.216441	0.001276	0.008378	0.109486	16.1026	15.1198	0.756	2.1924
2020-04-13 16:48:15	127.275301	127.978815	18.636776	0.699881	0.7	20689.243132	120.184825	148.143082	148.17111	8093.769919	...	0.007507	0.578589	0.216320	0.001283	0.008433	0.110001	16.1026	15.1198	0.766	2.1924
2020-04-13 16:48:20	127.696616	127.828510	18.967633	0.699940	0.7	20659.323792	119.981226	148.145629	148.17111	8080.924999	...	0.007501	0.578555	0.216928	0.001277	0.008427	0.110195	16.1026	15.1198	0.756	2.1924
2020-04-13 16:48:25	128.200408	128.112737	18.997359	0.699260	0.7	20743.472316	120.231323	148.006940	148.17111	8082.870058	...	0.007509	0.579640	0.217150	0.001275	0.008388	0.109362	16.1026	15.1198	0.756	2.1924
2020-04-13 16:48:30	128.044561	127.924522	18.465447	0.700233	0.7	20692.702652	120.078393	148.122538	148.17111	8077.325268	...	0.007498	0.578926	0.216951	0.001280	0.008394	0.109460	16.1026	15.1198	0.766	2.1924
2020-04-13 16:48:35	127.541773	127.934195	18.620404	0.699720	0.7	20694.890341	120.032655	148.013870	148.17111	8074.112488	...	0.007493	0.578907	0.216677	0.001278	0.008373	0.109723	16.1026	15.1198	0.766	2.1924

8 rows × 91 columns

特徴量の数が目的変数列を含めて91個であるので、\(K = 91 - 1 = 90\)となります。これを\(\mathbf{x}_{k}=(x_1, \ldots, x_N)_{k = 1, \ldots , K = 90} \in \mathbb{R}^{N}\)とします。 本稿ではアブソーバ液面レベル_PVの値を予測することを目的とし、この系列を \(\mathbf{y}\) とします。

これら \(\mathbf{x}_{k}\)、\(\mathbf{y}\) よりデータ \(\mathcal{D} = (\mathbf{x}_{p, p}, y_{p + n}) , \ldots , (\mathbf{x}_{N-n, p}, {y}_{N}) \in \mathcal{X} \times \mathcal{Y}\) から回帰モデル\(f:\mathcal{X} \rightarrow \mathcal{Y}\)に説明変数と目的変数の関係を学習させ、\(\mathbf{x}_{t, p}\) から \(n\) ステップ先の \(y_{t + n}\) を予測します。

データ \(D\) の要素はそれぞれ独立でかつ同一の分布から生じていると仮定し、予測先のデータである \(y_{t + n}\) も同様に仮定します。ここでは学習データとテストデータもそれぞれ同一の分布から生じていると仮定しますが（でないと先に進まない…）、実際には同一の分布からデータが生じないことが要因でモデルがうまくいかない場合は多々あるので、その場合は案件のドメイン知識を駆使して特徴量を個別に前処理したり、問題設定を改めたりする必要があります。

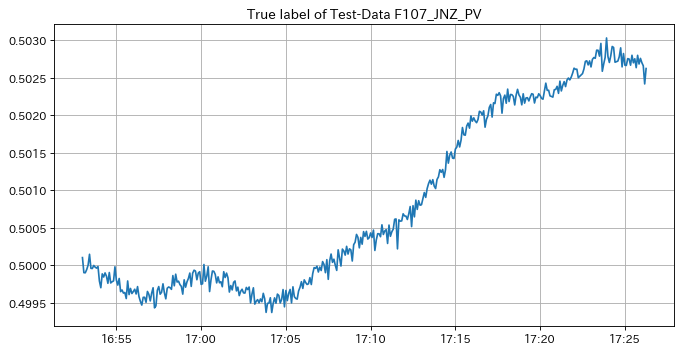
y = y_test

fig, ax = plt.subplots(1, 1, figsize=(10, 5), dpi=80)

begin = 60
window = 400

ax.set_title("True label of Test-Data F107_JNZ_PV")
ax.xaxis.set_major_formatter(DateFormatter("%H:%M"))
ax.plot(
    y.index[begin : begin + window],
    y[begin : begin + window],
    label="true",
)
ax.grid()

多重共線性の確認

データの特徴量間の相関係数からどの程度多重共線性が発生しているか確認します。ここでは特徴量の相関係数の絶対値が0.9以上であれば多重共線性があるとして、すべての特徴量間の相関係数を計算します。
横軸 - 縦軸が共に特徴量のラベルとなる相関行列で表し、それぞれの要素が特徴量間の相関係数となります。同じ特徴量間の相関係数は1なので対角成分は必ず１になり、相関係数の計算方法における対称性より相関行列は対称行列になります。以上を踏まえて計算すると多重共線性にあるペアは120個以上あることが確認でき、このまま重回帰分析を行うと推定精度が悪くなる可能性が高いです。

df_adjacency_corr = X_train.drop(
    ["アブソーバ液面レベル_PV"], axis=1
).corr()  # yを抜いた特徴量間の相関係数を計算
display(df_adjacency_corr)
print(
    "多重共線性にある特徴量のペアの数:{}".format(
        ((df_adjacency_corr.abs() >= 0.9).values.sum() - (X_train.shape[1] - 1)) // 2
    )
)  # 閾値0.9以上となるペアを1として、多重共線性にあるペアの数を算出

	気化器圧力_PV	気化器圧力_SV	気化器圧力_MV	気化器液面レベル_PV	気化器液面レベル_SV	気化器液面レベル_MV	気化器温度_PV	気化器ヒータ出口温度_PV	気化器ヒータ出口温度_SV	気化器ヒータ熱量_MV	...	反応器流入組成（CO2）_PV	反応器流入組成（C2H4）_PV	反応器流入組成（C2H6）_PV	反応器流入組成（VAc）_PV	反応器流入組成（H2O）_PV	反応器流入組成（HAc）_PV	セパレータ蒸気排出量_MV (Fixed)	アブソーバスクラブ流量_MV (Fixed)	アブソーバ還流流量_MV (Fixed)	気化器液体流入量_MV (Fixed)
気化器圧力_PV	1.000000e+00	7.039143e-01	-1.212237e-01	4.612649e-01	-3.773744e-13	1.689485e-01	4.717868e-01	-2.988823e-01	-3.075410e-01	-3.427893e-01	...	-2.026042e-01	3.896279e-01	-2.844527e-01	-3.113950e-01	-2.229185e-01	-3.848892e-01	3.770343e-13	7.937956e-03	-5.499938e-03	-3.775568e-13
気化器圧力_SV	7.039143e-01	1.000000e+00	1.073948e-03	5.904268e-01	-1.312093e-12	2.310670e-01	6.475319e-01	-4.141731e-01	-4.243152e-01	-4.728249e-01	...	-2.647471e-01	4.293766e-01	-4.760219e-01	-3.724326e-01	-1.743055e-01	1.016755e-01	1.312439e-12	6.555892e-04	-2.584163e-03	-1.312345e-12
気化器圧力_MV	-1.212237e-01	1.073948e-03	1.000000e+00	1.747519e-02	3.920082e-14	1.679311e-02	-1.169091e-02	-5.321883e-03	-5.635937e-03	-5.610424e-03	...	-4.457193e-03	5.813053e-02	5.260494e-03	1.161925e-02	3.974568e-02	1.888454e-01	-3.922023e-14	-2.090496e-03	-6.509716e-03	3.921476e-14
気化器液面レベル_PV	4.612649e-01	5.904268e-01	1.747519e-02	1.000000e+00	-2.109020e-12	2.294063e-01	2.880439e-01	-3.158880e-01	-3.154861e-01	-3.327451e-01	...	-2.734728e-01	4.965849e-01	-4.987493e-01	-3.503641e-01	-2.284870e-01	-5.571798e-02	2.108734e-12	1.063309e-02	-5.099661e-04	-2.109087e-12
気化器液面レベル_SV	-3.773744e-13	-1.312093e-12	3.920082e-14	-2.109020e-12	1.000000e+00	-2.432340e-14	-1.952277e-12	2.787496e-13	9.979289e-12	-1.737823e-14	...	-6.449066e-15	-4.229137e-13	-4.661178e-13	-1.047815e-14	3.490330e-16	1.988972e-13	-1.000000e+00	4.110047e-10	3.183434e-12	1.000000e+00
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
反応器流入組成（HAc）_PV	-3.848892e-01	1.016755e-01	1.888454e-01	-5.571798e-02	1.988972e-13	2.619016e-01	2.841070e-01	8.678396e-02	1.014959e-01	6.175553e-02	...	-2.559784e-01	-4.415656e-02	-1.570388e-02	-1.621675e-01	-1.832417e-01	1.000000e+00	-1.984429e-13	-3.663145e-03	1.124743e-02	1.986293e-13
セパレータ蒸気排出量_MV (Fixed)	3.770343e-13	1.312439e-12	-3.922023e-14	2.108734e-12	-1.000000e+00	2.448827e-14	1.952233e-12	-2.787582e-13	-9.989035e-12	1.831218e-14	...	6.234972e-15	4.229791e-13	4.653684e-13	1.145399e-14	4.711809e-16	-1.984429e-13	1.000000e+00	-4.110054e-10	-3.183662e-12	-1.000000e+00
アブソーバスクラブ流量_MV (Fixed)	7.937956e-03	6.555892e-04	-2.090496e-03	1.063309e-02	4.110047e-10	1.188697e-02	4.779807e-03	1.069773e-02	1.025276e-02	1.041235e-02	...	-7.419004e-03	2.082876e-03	1.619357e-03	5.868062e-03	-4.803479e-05	-3.663145e-03	-4.110054e-10	1.000000e+00	5.855828e-03	4.110068e-10
アブソーバ還流流量_MV (Fixed)	-5.499938e-03	-2.584163e-03	-6.509716e-03	-5.099661e-04	3.183434e-12	2.992598e-03	7.391152e-03	8.747490e-03	1.235267e-02	9.988123e-03	...	-1.861083e-03	-3.451958e-03	-7.675843e-04	1.285905e-02	7.803346e-03	1.124743e-02	-3.183662e-12	5.855828e-03	1.000000e+00	3.184109e-12
気化器液体流入量_MV (Fixed)	-3.775568e-13	-1.312345e-12	3.921476e-14	-2.109087e-12	1.000000e+00	-2.392250e-14	-1.952466e-12	2.772778e-13	9.958974e-12	-1.682763e-14	...	-7.200894e-15	-4.218381e-13	-4.640939e-13	-1.058591e-14	5.596322e-16	1.986293e-13	-1.000000e+00	4.110068e-10	3.184109e-12	1.000000e+00

90 rows × 90 columns

多重共線性にある特徴量のペアの数:128

実際にこのデータを用いて重回帰モデルを学習させてみましょう。 重回帰モデルは最小二乗法により以下のように学習され、予測系列 \(\hat{\mathbf{y}}\) を出力します。

(1)\[\begin{eqnarray} \hat{\mathbf{y}}&=& \mathbf{X} \mathbf{b} \\ \mathbf{b} &=& (\mathbf{X}^{\mathsf{T}} \mathbf{X})^{-1} \mathbf{X}^{\mathsf{T}} \mathbf{y} \end{eqnarray}\]

ここで \(\mathbf{x}_{k}=(x_1, \ldots, x_N)_{k = 1, \ldots , K = 90}\)を \(\mathbf{X}_{n,p}\) に変換する関数を定義します(後々また使います)。
また本稿では \(p=20\)、\(n = 6\) と固定して後々紹介する回帰モデルの結果と比較します。まず学習させたモデルに学習データの説明変数を入力して予測値を見てみましょう。

def to_multiple_timeseries_array(X, y, p, n):
    X_lagged_index_ar = np.arange(p).reshape(1, -1) + np.arange(X.shape[0] - p).reshape(
        -1, 1
    )
    X_lagged_ar = X.values[X_lagged_index_ar]

    X_lagged_multi_times_ar = (
        X_lagged_ar[:-n].transpose(0, 2, 1).reshape(X_lagged_ar.shape[0] - n, -1)
    )  # 説明変数、(N - p - n + 1, p * 特徴量数)-行列
    y_target_ar = y.values[p:].reshape(-1, 1)[n:]  # 目的変数、(N - p - n + 1, 1)-行列
    return X_lagged_multi_times_ar, y_target_ar

from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import StandardScaler

p = 20  # 直前ステップ数, p
n = 6  # 予測先ステップ数, n

X_train_ar, y_train_ar = to_multiple_timeseries_array(
    X_train, y_train, p, n
)  # 説明変数と目的変数を生成

multi_reg = LinearRegression(normalize=True)
multi_reg.fit(X_train_ar, y_train_ar)  # 重回帰モデルでfitting

y_train_mulreg_ar_pred = multi_reg.predict(X_train_ar)  # 学習データで予測

fig, ax = plt.subplots(1, 1, figsize=(10, 5), dpi=80)

begin = 60
window = 400
lag = p

ax.set_title("In-Sample Training-Data Forecast with Multiple Regression")
ax.xaxis.set_major_formatter(DateFormatter("%H:%M"))
ax.plot(
    y_train.index[begin : (begin + window)],
    y_train_ar[(begin - lag) : (begin - lag + window)],
    label="true",
)
ax.plot(
    y_train.index[begin : (begin + window)],
    y_train_mulreg_ar_pred[(begin - lag) : (begin - lag + window)],
    label="pred (Multiple Regression)",
)
ax.grid()
ax.legend()

plt.show()

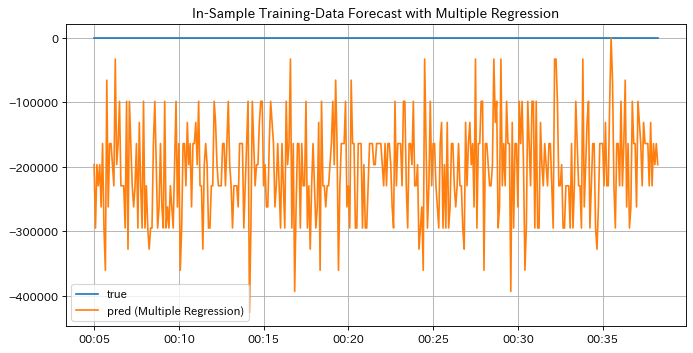
どうやらモデルが上手くfittingできていないようです。学習済みモデルを評価する際テストデータに対する予測結果のみ見れば良いように思えるかもしれませんが、このように学習データに対する予測結果がラベルから外れていた場合根本的にモデル設計が間違っていることがあるので念のため確認しましょう。

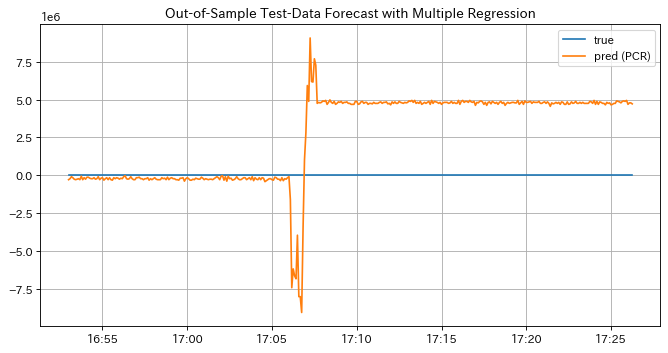
では次にテストデータの予測結果を見てみますと、やはり下のグラフのようにテストデータの予測結果もラベルから大きく逸脱してしまい、モデルの学習が完全に失敗していることが確認できます。

X_test_ar, y_test_ar = to_multiple_timeseries_array(X_test, y_test, p, n)

y_test_mulreg_ar_pred = multi_reg.predict(
    X_test_ar
)  # テストデータを学習済みモデルで予測

fig, ax = plt.subplots(1, 1, figsize=(10, 5), dpi=80)

begin = 60
window = 400
lag = p

ax.set_title("Out-of-Sample Test-Data Forecast with Multiple Regression")
ax.xaxis.set_major_formatter(DateFormatter("%H:%M"))
ax.plot(
    y_test.index[begin : (begin + window)],
    y_test_ar[(begin - lag) : (begin - lag + window)],
    label="true",
)
ax.plot(
    y_test.index[begin : (begin + window)],
    y_test_mulreg_ar_pred[(begin - lag) : (begin - lag + window)],
    label="pred (PCR)",
)
ax.grid()
ax.legend()

plt.show()

PCRモデル

多重共線性を回避して予測精度を上げたい、しかしどの説明変数が目的変数に効いているか明確ではないので説明変数はなるべく外したくない、案件を進めていく上でそのようなケースに遭遇することは珍しくないと思われます。そこで説明変数を外さずにモデル単体でそれらに対処できる回帰モデルの一つとして PCR (Principal Component Regression) が挙げられます。
PCR は PCA で得られた主成分を使い重回帰分析を行う手法です。 PCA (Principal Component Analysis) とは \(M\) 次元データ \(\mathbf{X}\) を、特徴量がお互いに無相関でかつ圧縮した際の元の\(\mathbf{X}\)に対する情報損失量が少なくなるよう \(m(<M)\) 次元の主成分 \(\mathbf{T}\) に圧縮する次元圧縮法です。元のデータを無相関化することで多重共線性を回避することができるので、圧縮された主成分を重回帰分析にかけることで精度よく予測することが可能となります。
ここではPCAについて簡単に言及しますが、詳しい説明はこちらの記事を参照してください。

まず主成分 \(\mathbf{T}\) の求め方について説明します。
\(\mathbf{X}\) に関する固有ベクトル \(\mathbf{p}_{n(n = 1, \ldots , M)}\) は以下の固有値問題の式を解くことで得られます。

(2)\[\begin{equation} \left(\mathbf{X} ^ \mathsf{T} \mathbf{X} - \lambda \mathbf{E} \right) \mathbf{p} = 0 \end{equation}\]

この固有ベクトル \(\mathbf{p}_{n}\) を必要な主成分数 \(m\) の数だけ横に並べた行列 \(\mathbf{P}\) を用いることで、主成分 \(\mathbf{T}\) を次の式のように表せます。

(3)\[\begin{equation} \mathbf{T} = \mathbf{X} \mathbf{P} \end{equation}\]

またこの時固有値はデータの分散と一致し元データの情報量と対応しているため、情報損失量を直接計算することができます。 すべての主成分軸における分散（=固有値） \(\lambda_k\) の総和 \(\sum _ {k = 1} ^ {M}\lambda _k\) に対する第１〜 \(a\) までの主成分軸における分散の総和の比率を計算することで情報損失量を計算でき、これを累積寄与率といいます。

(4)\[\begin{equation} m = \underset{\mathrm{a}}{\text{argmax}} \dfrac{\displaystyle \sum _ {k = 1} ^ {a}\lambda _k}{\displaystyle \sum _ {k = 1} ^ {M}\lambda _k} < 0.90 \end{equation}\]

ここで、与えた累積寄与率の閾値（ここでは0.90とします）を越えない最大の主成分数を \(m\) とし、元データ \(\mathbf{X}\) を主成分 \(\mathbf{T}_{m}\) に変換します。 \(\mathbf{T}_m\) から時刻 \(t\) の直近 \(p\) サンプル分を１つのベクトルに引き延ばす処理を \(t = p \sim N - n\) まで繰り返して行列 \(\mathbf{T}_{m, n, p} \in \mathbb{R}^{(N - p - n + 1)\times (p \times m) }\) を得ます。 この \(\mathbf{T}_{m,n,p}\) を説明変数として各サンプルの\(n\)サンプル後の系列 \(\mathbf{y}_{n}=(y_{p + n}, \ldots, y_{N}) \in \mathbb{R}^{N - p - n + 1}\) を目的変数とします。また説明変数、目的変数共に正規化しておきます。
あとは通常の重回帰分析と同様に \(\mathbf{T}_{m,n,p}\) と \(\mathbf{y}_{n}\) の関係性を最小二乗法に基づいて解くことで予測系列 \(\hat{\mathbf{y}}\) を予測します。 以上が PCR による予測の一連の流れとなります。

(5)\[\begin{align} \hat{\mathbf{y}} &= \mathbf{T}_{m, n, p}\mathbf{b} + \mu\\ \mathbf{b} &= (\mathbf{T}_{m, n, p}^{\mathsf{T}} \mathbf{T}_{m, n, p})^{-1} \mathbf{T}_{m, n, p}^{\mathsf{T}} \mathbf{y} \end{align}\]

実際にscikit-learnのPCAクラスを用いて実装してみましょう。

from sklearn.decomposition import PCA

PCA_train = PCA()  # PCAインスタンスを生成
X_reduced_train = pd.DataFrame(
    PCA_train.fit_transform(StandardScaler().fit_transform(X_train)),
    index=X_train.index,
)
# 標準化したXをPCAで主成分変換

contribution_threshold = 0.90  # 累積寄与率の閾値

ev_ratio = PCA_train.explained_variance_ratio_  # 主成分数ごとの寄与率
ev_ratio_stack = np.hstack([0, ev_ratio.cumsum()])  # 累積寄与率を計算
ev_ratio_stack = ev_ratio_stack[
    ev_ratio_stack < contribution_threshold
]  # 累積寄与率が95%未満となる最大の主成分数を選定
estimated_ncomp = ev_ratio_stack.shape[0] - 1  # 累積寄与率

fig, ax = plt.subplots(1, 1, figsize=(10, 8), dpi=50)
ax.set_title("Cumulative Contributuion Rate", fontsize=24)
ax.set_xlabel("Number of Principal Components", fontsize=20)
ax.set_ylabel("Cumulative Contribution Rate", fontsize=20)
ax.plot(ev_ratio_stack)
ax.tick_params(labelsize=18)
ax.grid()
plt.show()
print(
    "累積寄与率{:.2f}未満となる最大の主成分数：{}".format(
        contribution_threshold, estimated_ncomp
    )
)

累積寄与率0.90未満となる最大の主成分数：13

累積寄与率の閾値を0.90としたとき、それ未満となる最大の主成分数は13となりました。 これは初めの１個目から13個目の主成分で元データの情報の約90%をカバーしているということを表しています。 元データの特徴量の数が120個以上だったことを踏まえると大分情報を圧縮できそうです。
では累積寄与率から得た13個の主成分を用いてPCRモデルを学習させ、学習データによる予測結果を見てみましょう。

PCR = LinearRegression(normalize=True)
X_reduced_train_ar, y_train_ar = to_multiple_timeseries_array(
    X_reduced_train.iloc[:, :estimated_ncomp], y_train, p, n
)  # 主成分行列(T - p - n, p * 主成分数)を主成分行列((T - p - n) * p * 主成分数)
PCR.fit(X_reduced_train_ar, y_train_ar)  # 主成分とyの関係をPCRモデルで学習

y_train_pcr_ar_pred = PCR.predict(
    X_reduced_train_ar
)  # 学習データを学習済みPCRモデルに適用

fig, ax = plt.subplots(1, 1, figsize=(10, 5), dpi=80)

begin = 60
window = 400
lag = p

ax.set_title("In-Sample Training-Data Forecast with PCR")
ax.xaxis.set_major_formatter(DateFormatter("%H:%M"))
ax.plot(
    y_train.index[begin : (begin + window)],
    y_train_ar[(begin - lag) : (begin - lag + window)],
    label="true",
)
ax.plot(
    y_train.index[begin : (begin + window)],
    y_train_pcr_ar_pred[(begin - lag) : (begin - lag + window)],
    label="pred (PCR)",
)
ax.grid()
ax.legend()

plt.show()

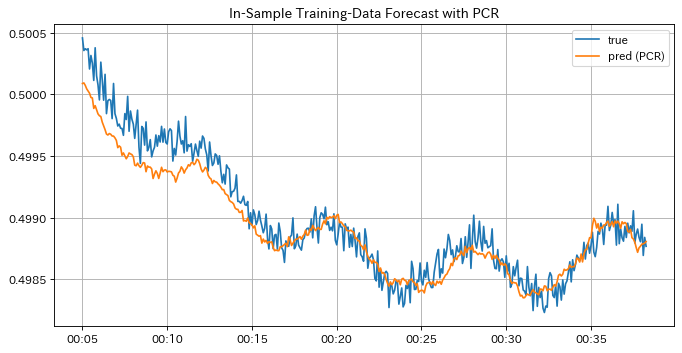
学習データを用いた予測結果をみると、通常の重回帰モデルの結果と比べラベルのトレンドをしっかり追従できているのでPCRモデルの学習自体は出来ていると言えそうです。
次にテストデータによるPCRモデルの予測結果を見てみましょう。

X_reduced_test = pd.DataFrame(
    PCA_train.transform(StandardScaler().fit_transform(X_test)), index=X_test.index
)
# 学習済みPCAモデルから標準化済みテストデータを主成分化
X_reduced_test_ar, y_test_ar = to_multiple_timeseries_array(
    X_reduced_test.iloc[:, :estimated_ncomp], y_test, p, n
)

y_test_pcr_ar_pred = PCR.predict(
    X_reduced_test_ar
)  # テストデータを学習済みPCRモデルに適用

fig, ax = plt.subplots(1, 1, figsize=(10, 5), dpi=80)

begin = 60
window = 400
lag = p

ax.set_title("Out-of-Sample forecast with PCR / Scikit-learn")
ax.xaxis.set_major_formatter(DateFormatter("%H:%M"))
ax.plot(
    y_test.index[begin : (begin + window)],
    y_test_ar[(begin - lag) : (begin - lag + window)],
    label="true",
)
ax.plot(
    y_test.index[begin : (begin + window)],
    y_test_pcr_ar_pred[(begin - lag) : (begin - lag + window)],
    label="pred (PCR)",
)
ax.grid()
ax.legend()

plt.show()

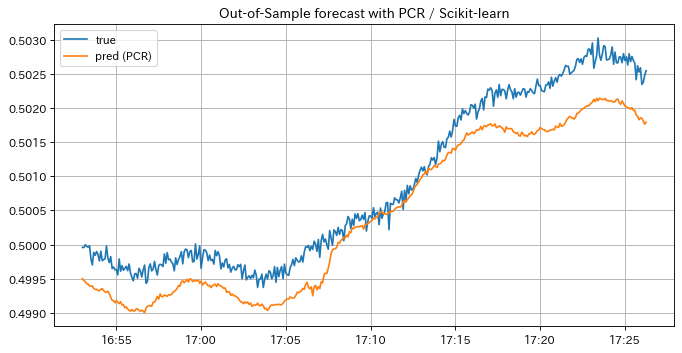
通常の重回帰モデルの予測結果と違い、PCRによる予測結果がラベルの値とスケールが等しく、ラベルのトレンドに追従していることが確認できます。 この結果からPCRによって多重共線性が回避して未来の値を予測できることが分かりました。

PLS回帰モデル

PCRを利用することで多重共線性を回避して予測できることが確認できましたが、PCRでは特徴量の無相関化において \(\mathbf{X}\) の情報のみしか用いておらず、\(\mathbf{y}\) との関係は考慮していません。 \(\mathbf{X}\) の中に目的変数 \(\mathbf{y}\) と全く無相関な特徴量が含まれていた場合、良い予測精度が得られない可能性があります。
PLS (Partial Least Squares) モデルは \(\mathbf{X}\) と \(\mathbf{y}\) の関係から潜在的な因子を抽出する回帰モデルです。 PLSは主に計量化学の分野でスペクトル解析などに用いられてきた回帰分析手法ですが、説明変数である \(\mathbf{X}\) の特徴量間の相関と目的変数 \(\mathbf{y}\) との相関を同時に考慮しながら潜在変数を抽出するので、時系列データに対しても多重共線性を回避しつつ、より高い予測精度が得られることが期待されます。

PLSのモデル学習手順としてはまず、\(\mathbf{X}\) と \(\mathbf{y}\) から スコア \(\mathbf{t}_1\) という潜在変数を計算します。 このスコアという言葉はPCAでいう主成分のようなものであり、射影した空間における座標に相当します。 この時スコアを計算する際の重みベクトル \(\mathbf{w}_1\) は \(\mathbf{t}_1\) の分散（情報のばらつき具合）が最大になるように決める必要があり、これは \(\mathbf{X}\) と \(\mathbf{y}\) の共分散から算出されます（なぜ共分散なのかはラグランジュの未定乗数法から導けますが、証明はここでは割愛します）。

(6)\[\begin{eqnarray} \mathbf{t}_1 &=& \mathbf{X}\mathbf{w}_1 \\ \mathbf{w}_1 &=& \dfrac{\mathbf{X}^{\mathrm{T}} \mathbf{y}}{\| \mathbf{X}^{\mathrm{T}} \mathbf{y} \|} \end{eqnarray}\]

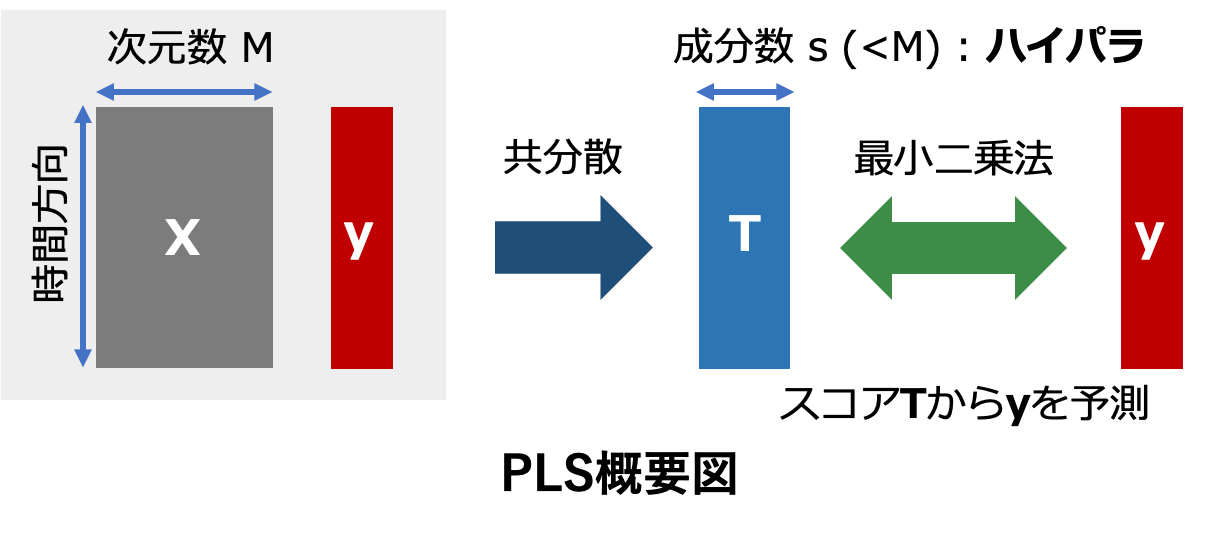
次にスコア \(\mathbf{t}_1\) から \(\mathbf{X}\) と \(\mathbf{y}\) を推定する係数ベクトルである ローディングベクトル \(\mathbf{p}_1\) と \({q}_1\) を最小二乗法を用いて求めます。

(7)\[\begin{eqnarray} \mathbf{p}_1 &=& \dfrac{\mathbf{X}^{\mathrm{T}} \mathbf{t}_1}{ \mathbf{t}^{\mathrm{T}}_1 \mathbf{t}_1 } \\ q_1 &=& \dfrac{\mathbf{y}^{\mathrm{T}} \mathbf{t}_1}{ \mathbf{t}^{\mathrm{T}}_1 \mathbf{t}_1 } \end{eqnarray}\]

これで第１スコアの重み \(\mathbf{w}_1\) とローディングベクトル \(\mathbf{p}_1\)、\({q}_1\) が求められました。 第２スコア \(\mathbf{t}_2\) を求める際は \(\mathbf{X}\) と \(\mathbf{y}\) から第１成分で表現できる情報を引いた上で第１スコアの場合と同様に計算します。 この時 \(\mathbf{w}_1\) と \(\mathbf{w}_2\) は直交しており、繰り返すごとに表現できる情報が増えていることを示しています。

(8)\[\begin{eqnarray} \mathbf{X}_{2} &=&\mathbf{X} - \mathbf{t}_1 \mathbf{p}_1^{\mathrm{T}} \\ \mathbf{y}_{2} &=&\mathbf{y} - q_1 \mathbf{t}_1 \end{eqnarray}\]

この処理を指定した回数（成分数）まで繰り返すことで得られた重みとローディングベクトルを成分数方向に並べることで、行列 \(\mathbf{W}\)、\(\mathbf{P}\)、\(\mathbf{q}\) が求められます。 これらを用いて最終的にPLSモデルによる予測系列 \(\mathbf{\hat{y}}\) は以下のように表されます。

(9)\[\begin{eqnarray} \mathbf{\hat{y}}&=&\mathbf{X}\mathbf{W^*}\mathbf{q} \\ \mathbf{W}^*&=&\mathbf{W} ({\mathbf{P^{\mathrm{T}} W}})^{-1} \end{eqnarray}\]

PLSモデルの構築の際、問題となるのが最適な成分数(上記処理の繰り返し数)を決めなければならないことです。 成分数の決め方は一般的にはクロスバリデーションとグリッドサーチによるハイパーパラメータ探索が使われたりしますが、今回のような時系列データの場合は取り扱いが難しいので注意が必要です。要件に合わせて、クロスバリデーションにおける評価指標（相関係数、RMSEなど）を変えたりして決めると良いでしょう。 より詳しいPLSの説明は参考文献[2]~[5]などを参照ください。

今回は \(\mathbf{X}_{n,p} \in \mathbb{R}^{(N - p - n + 1) \times (p \times (K + 1)) }\) を説明変数、\(\mathbf{y}_{n}=(y_{p + n}, \ldots, y_{N}) \in \mathbb{R}^{N - p - n + 1}\) を目的変数としてPLSモデルに学習させます。このようにモデルの入出力データの形式は本稿での重回帰分析でのそれと同じです。
残りの条件は上記の重回帰分析、PCRの場合と同じで、時刻 \(t\) の \(n\) サンプル後の \(y_t\) を予測することが目的です。

ではsklearnのPLSクラスを用いた実装を見てみましょう。

from sklearn.cross_decomposition import PLSRegression, PLSSVD

n_components = 12  # 成分数
PLS_reg = PLSRegression(n_components=n_components, scale=True)  # PLSインスタンス生成

PLS_reg.fit(X_train_ar, y_train_ar)
y_train_pls_ar_pred = PLS_reg.predict(X_train_ar)

fig, ax = plt.subplots(1, 1, figsize=(10, 5), dpi=80)

begin = 60
window = 400
lag = p

ax.set_title("In-Sample forecast compareing with PCR and PLS / Scikit-learn")
ax.xaxis.set_major_formatter(DateFormatter("%H:%M"))
ax.plot(
    y_train.index[begin : (begin + window)],
    y_train_ar[(begin - lag) : (begin - lag + window)],
    label="true",
)
ax.plot(
    y_train.index[begin : (begin + window)],
    y_train_pcr_ar_pred[(begin - lag) : (begin - lag + window)],
    label="pred (PCR)",
)
ax.plot(
    y_train.index[begin : (begin + window)],
    y_train_pls_ar_pred[(begin - lag) : (begin - lag + window)],
    label="pred (PLS Regression)",
)
ax.grid()
ax.legend()

plt.show()

y_test_pls_ar_pred = PLS_reg.predict(X_test_ar)

fig, ax = plt.subplots(1, 1, figsize=(10, 5), dpi=80)

begin = 60
window = 400
lag = p

ax.set_title("Out-of-Sample forecast with PLS / Scikit-learn")
ax.xaxis.set_major_formatter(DateFormatter("%H:%M"))
ax.plot(
    y_test.index[begin : (begin + window)],
    y_test_ar[(begin - lag) : (begin - lag + window)],
    label="true",
)
ax.plot(
    y_test.index[begin : (begin + window)],
    y_test_pcr_ar_pred[(begin - lag) : (begin - lag + window)],
    label="pred (PCR)",
)
ax.plot(
    y_test.index[begin : (begin + window)],
    y_test_pls_ar_pred[(begin - lag) : (begin - lag + window)],
    label="pred (PLS Regression)",
)
ax.grid()
ax.legend()

plt.show()

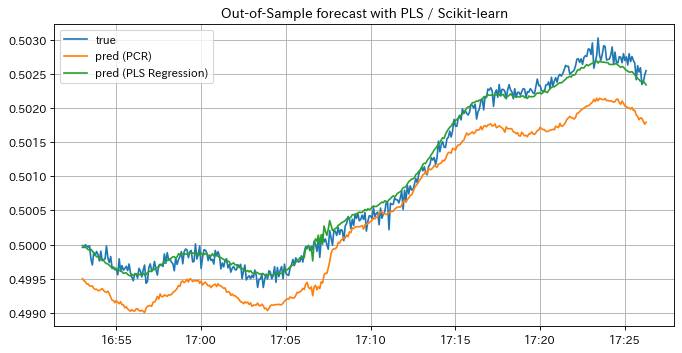
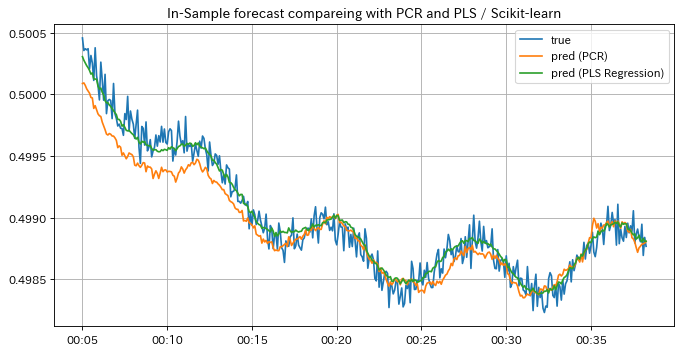
PLSモデルの予測結果を見てみましょう。学習データに対する予測結果はPCRと同様にラベルに追従しており、上手くfittingしているように見えます。 一方テストデータに対する予測結果はPCRのそれよりラベルに漸近している区間が広く、予測精度が向上したことが分かります。 このようにPLSモデルを用いることで予測精度をより広い区間において向上させることができましたが、以下の例のように別区間だとPCRの方が予測結果が良い場合もあるので、要件に応じて適宜使い分けると良いでしょう。

fig, ax = plt.subplots(1, 1, figsize=(10, 5), dpi=80)

begin = 590
window = 400
lag = p

ax.set_title("Out-of-Sample forecast with PLS / Scikit-learn")
ax.xaxis.set_major_formatter(DateFormatter("%H:%M"))
ax.plot(
    y_test.index[begin : (begin + window)],
    y_test_ar[(begin - lag) : (begin - lag + window)],
    label="true",
)
ax.plot(
    y_test.index[begin : (begin + window)],
    y_test_pcr_ar_pred[(begin - lag) : (begin - lag + window)],
    label="pred (PCR)",
)
ax.plot(
    y_test.index[begin : (begin + window)],
    y_test_pls_ar_pred[(begin - lag) : (begin - lag + window)],
    label="pred (PLS Regression)",
)
ax.grid()
ax.legend()

plt.show()

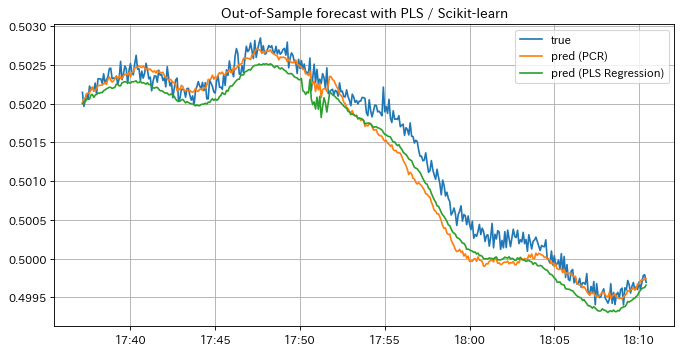
またPLSモデルの予測結果はハイパーパラメータである成分数の値によって大きく変動し、成分数が大きいほど潜在変数の数が多くなるので過学習しがちです。選択した成分数での相関係数やRMSEが良くても、予測グラフがトレンドを追えてない・他の成分数での予測結果の方が要件的に望ましい等あるので、用いる案件に応じて成分数の数といったハイパーパラメータを選択する方がいいかも知れません。

小括

本稿では説明変数を外さずに多重共線性を回避できる予測モデルとして PCR モデル、 PLS モデルを解説しました。 いずれも単純な重回帰分析と比較して、多重共線性のあるデータに対しても予測精度を向上させることができますが、RMSEや相関係数の値を向上させる、要件にマッチする予測グラフを得る等の要件によって使うモデルやハイパーパラメータを変える必要があります。 どのモデルを使うか、ハイパーパラメータをどう調整するかは実際にモデルを学習させて予測結果を見ながら、案件のドメイン知識を駆使したり、要件を見直したりすることで使い分けると良いでしょう。
また目的変数と全く相関が無い・ほぼ変動しない特徴量が予め分かっている場合、外した方がPCRでもPLSでも予測精度は向上することが多いです。 実際に案件でこれらを用いる際には、必要ないと判断した特徴量を１つずつ外しながらモデルの予測結果を逐次確かめていくと良いです。

参考文献

[1] Process Improvement Using Data
[2] PLS回帰におけるモデル選択
[3] 部分的最小二乗回帰(Partial Least Squares Regression, PLS)～回帰分析は最初にこれ！～
[4] PLS(部分的最小二乗法)入門
[5] ソフトセンサー入門　基礎から実用的研究まで