スパースモデリング(発展編)#
より高度なスパース推定#
前々回スパースモデリング(基本編)では、基本のスパースモデリングとしてLASSOを題材にスパースな解が得られる原理を視覚的に説明しました。
またスパースモデリング(応用編)では、正則化項を良い感じにアレンジすることで問題設定に応じた特徴的なスパース性が誘導できることを確認しました。
本稿ではさらに発展的な内容としてTrace LASSOとGraphical LASSOを紹介します。
いずれの手法も技術的難易度が高めですが、使いこなせば大規模データ解析で非常に有効な武器となりますので臆せず読んでみてください!
データ読み込み#
データの読み込みと前処理については前回と同様に行いたいと思います。
ここでは個々の処理について細かく説明しませんので、疑問がある場合はスパースモデリング(基本編)を参照してください。
import warnings
warnings.filterwarnings('ignore')
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# matplotlibでは日本語にデフォルトで対応していないので、日本語対応フォントを読み込む
plt.rcParams['font.family'] = 'BIZ UDGothic' # Windows
# plt.rcParams['font.family'] = 'Hiragino Maru Gothic Pro' # Mac
# 使えるフォント一覧は以下のコードで取得できます。
# import matplotlib.font_manager
# [f.name for f in matplotlib.font_manager.fontManager.ttflist]
pd.set_option("display.max_rows", 10)
pd.set_option("display.max_columns", 10)
fpath = '../data/2020413.csv'
df = pd.read_csv(fpath, index_col = 0, parse_dates = True, encoding = 'shift-jis')[::5]
# std < 1e-10の数値列をdropする
drop_list = list(df.describe().loc['std'] < 1e-10)
df = df.drop(columns = df.columns[drop_list])
# 相関行列の要素のうち、条件を満たすものを要素を1、満たしていない要素を0とする、隣接行列を取得する。
# ここでは、後の計算の簡略化のために対角成分も残したまま取り扱う。
# 今回は相関係数の絶対値が0.85より大きいことを条件とする。
Adjacency = np.array(df.corr().abs() > 0.85).astype('int')
# グラフ理論によると隣接行列のべき乗(ただし非ゼロ要素は都度すべて1に変換する)は、適当回数遷移した後に接続している要素を示す。
# 例えばi行の非ゼロ要素のインデックス集合は、i番目の要素と接続している要素の集合となる。
# これを利用して、先ほど定義した隣接行列から、多重共線性の危険性のある列のグループを抽出する
while True:
Adjacency_next = np.dot(Adjacency, Adjacency).astype('int')
Adjacency_next[Adjacency_next != 0] = 1
if(np.all(Adjacency_next == Adjacency)):
break
else:
Adjacency = Adjacency_next
multicol_list = [np.where(Ai)[0].tolist() for Ai in Adjacency]
# 要素が1つだけのグループ、および重複のあるグループを取り除き、インデックスの最も若い列を残して、それ以外を削減対象とする。
# 削減対象以外の残す列のインデックスを取得する。
extract_list = sorted(list(set(sum([m[:1] for m in multicol_list], []))))
# 多重共線性の危険性を排除したデータセットを得る。
df_corr = df.iloc[:,extract_list]
# 以降では相関係数で次元削減したデータセットを用いる
df = df_corr.copy()
from sklearn.model_selection import train_test_split
X_train, X_validation, y_train, y_validation = train_test_split(df[df.columns.difference(['気化器圧力_PV'])], df[['気化器圧力_PV']], test_size=0.2, shuffle=False)
from sklearn.preprocessing import StandardScaler
# 正規化を行うオブジェクトを生成
SS_X_train = StandardScaler()
SS_X_validation = StandardScaler()
SS_y_train = StandardScaler()
SS_y_validation = StandardScaler()
# fit_transform関数は、fit関数(正規化するための前準備の計算)と
# transform関数(準備された情報から正規化の変換処理を行う)の両方を行う
X_train[:] = SS_X_train.fit_transform(X_train)
X_validation[:] = SS_X_validation.fit_transform(X_validation)
y_train[:] = SS_y_train.fit_transform(y_train)
y_validation[:] = SS_y_validation.fit_transform(y_validation)
Show code cell source
import numpy as np
# L が M の約数になっていなかった場合は例外処理に回す
class LMUndivisibleError(Exception):
pass
def time_window_x(x, l, m, n, s):
nrow, ncol = x.shape
nsample_org = nrow - m + 1 - n # 元データの切り出しに使われる範囲のサイズ
nsample = (nrow - m - n ) // s + 1 # 出力のサンプル数
# l が m の約数になっていなかった場合は例外を発生
nsplit, rem = divmod(m, l)
if rem != 0:
raise LMUndivisibleError
#説明変数
x_transformed = np.zeros((nsample, nsplit, ncol), dtype=float) # 出力の格納先
for i, st in enumerate(range(0, nsample_org, s)):
en = st + m
tmpX = x[st:en, :]
# L ごとに切って配列の次元を増やしたあと平均して次元をもとに戻す
x_transformed[i,:,:] = tmpX.reshape(nsplit, l, ncol).mean(axis=1)
return x_transformed
def time_window_y(y, m, n, s):
res = y[n+m-1::s,:].reshape((-1,1))
return res
def time_window_transform(x, y, l, m, n, s):
if m % l != 0:
raise LMUndivisibleError
x_transformed = time_window_x(x, l, m, n, s)
nrow = x_transformed.shape[0]
y_transformed = time_window_y(y, m, n, s)[:nrow,:]
return x_transformed, y_transformed
L, M, N, S = 1, 12, 1, 1
X_train_lmns, y_train_lmns = time_window_transform(X_train.values, y_train.values, l=L, m=M, n=N, s=S)
X_validation_lmns, y_validation_lmns = time_window_transform(X_validation.values, y_validation.values, l=L, m=M, n=N, s=S)
X_train_lmns_flat = X_train_lmns.reshape(len(X_train_lmns), int(X_train_lmns.size/len(X_train_lmns)), order='F')
X_validation_lmns_flat = X_validation_lmns.reshape(len(X_validation_lmns), int(X_validation_lmns.size/len(X_validation_lmns)), order='F')
よく使用する関数#
ここも前回同様、学習モデルの性能を確認する関数として score 関数、学習モデルのパラメータを可視化する関数として heatmap 関数の2つを使用することとします。
個々の関数の詳細はスパースモデリング(基本編)を参照してください。
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
x_tick_label = pd.date_range(y_validation.index[0], y_validation.index[-1], freq='10min')
x_tick_loc = [y_validation.index.get_loc(label) for label in x_tick_label]
def score(y, y_hat):
mae = mean_absolute_error(y, y_hat)
rmse = np.sqrt(mean_squared_error(y, y_hat))
corr = np.corrcoef(y, y_hat, rowvar=False)[0,1]
r2 = r2_score(y, y_hat)
print(f'MAE\t: {mae}')
print(f'RMSE\t: {rmse}')
print(f'CORR\t: {corr}')
print(f'R2\t: {r2}')
plt.figure(figsize=[8,6], dpi=200)
plt.plot(y, label='実測値')
plt.plot(y_hat, label='予測値')
plt.title('気化器圧力_PV')
plt.xticks(x_tick_loc, x_tick_label.strftime('%H:%M:%S'), rotation=40)
plt.legend()
plt.show()
return pd.DataFrame(np.array([[mae, rmse, corr, r2]]), columns = ['mae', 'rmse', 'corr', 'r2'])
def heatmap(coef, scale = None):
plt.figure(figsize=[8,6], dpi=200)
if(scale is None):
sns.heatmap(coef.reshape(X_validation.shape[1],-1), center=0, cmap="bwr")
plt.title('各パラメータ $\omega_i$ の推定値')
else:
sns.heatmap(coef.reshape(X_validation.shape[1],-1), center=0, cmap="bwr", vmin=-scale, vmax=scale)
plt.title(f'各パラメータ $\omega_i$ の推定値:色調範囲[{-scale}, {scale}]')
plt.xticks(np.arange(M)+0.5, [f'-{(m+1)*5}s ~ -{m*5}s'for m in np.arange(M)][::-1], rotation=10, fontsize=5)
plt.yticks(np.arange(X_validation.shape[1])+0.5, X_validation.columns, rotation=0, fontsize=5)
plt.xlabel("窓内の時間遅れ")
plt.ylim(X_validation.shape[1],0)
plt.grid()
plt.show()
Trace LASSO#
発展編1つめはTrace LASSOと呼ばれる手法です。
多くの文献ではTrace norm regularizationと呼ぶことが多いようですが、統一感を出したいのでここではTrace LASSOと呼ぶこととします。
いよいよ難しくなってきましたが順を追って確認していきたいと思います。
まず前提として、今まで見てきたスパースモデリング(基本編)やスパースモデリング(応用編)ではすべてのパラメータは列ベクトル\(\omega\)として解析してきました。
すなわち、どのセンサーに属しているか、あるいはどの時間遅れかといったことは考慮せず、一律に列ベクトル\(\omega\)の1つの要素として表現しています。
もちろんグループ構造を入れたGroup LASSOや差分構造を入れたFused LASSOも見てきましたが、これらは列ベクトル\(\omega\)に後付けで構造情報を付与したに過ぎません。
それに対して\(W\)は、例えば異なるセンサーを行方向に異なる時間遅れを列方向としたパラメータの行列を意味し、言うなれば今まで見てきたパラメータのヒートマップをそのまま当てはめたようなパラメータ行列となっています。
このようにベクトルではなく行列のまま解析することで、行列に内在した情報を保てるメリットがあります。
次元圧縮(後編:その他の手法)の非負値行列因子分解(NMF)と同様に、パラメータ行列の行方向or列方向に類似した特徴パターンがあると仮定できる場合に、類似特徴パターンをひとまとめに同一視して解釈した方が直感的に自然です。
例えば本稿で取り扱う多変量センサーデータの場合、各センサーの重みで構成される特徴パターンが複数あり、それぞれが時間窓のどこにどの程度出現するか、という解釈を行うことで全体の情報を要約することができます。
行方向と列方向を逆に見て、時間窓の各時間遅れの重みで構成される特徴パターンが複数あり、それぞれがセンサーのどこにどの程度出現するか、という解釈もできます(これらは本質的には同一の解釈です)。
Trace LASSOでは、不要な特徴パターンを削ぎ落とした少数の本質的な特徴パターンを炙り出します。
特に今回のデータにおいては、行方向はセンサーについての空間的な情報、列方向は時間遅れについての時間的な情報と考えることができ、今までのような行列を壊した解析のみでは獲得できない時空間的な関係性を考慮した解釈を行うことができます。
最適化問題中の\(\|\cdot\|_{\mathrm{trace}}\)はトレースノルムで、行列\(W\)の特異値を\(\sigma_1,\ldots,\sigma_R\)とすると次のように表現されます。
ここで\(R\)は特異値の個数で、一般には行列\(W\)の行数or列数の小さい方に一致します。
特異値分解については次元圧縮(前編:主成分分析)に詳しく掲載していますが、ここにもあるようにTrace LASSOは特異値分解を用いた低ランク近似をスパースに行う手法とみなすことができます。
つまり、Trace LASSOでは正則化項としてパラメータ行列のトレースノルム\(\|\cdot\|_{\mathrm{trace}}\)を課すことで、特異値に関するスパース推定を実行しています。
次元圧縮(前編:主成分分析)での特異値分解を用いた次元圧縮では、特異値の小さい順に0と置き換えて圧縮していましたが、ここをもう少し統計的にスパース推定の枠組みで縮約推定を行うのがTrace LASSOです。
Trace LASSOの使い所ですが、こちらも発想は次元圧縮(前編:主成分分析)とも近く、例えば時空間構造を考慮したパラメータ行列\(W\)を低ランクで近似することで、時間方向(あるいは空間方向)に目的変数への影響の与え方が同じようなセンサー(時間遅れ)をひとまとめにして、本質的に同質のひとつのパラメータとみなすことができます。
パラメータ行列を\(W=U\Sigma V^{\top}\)と特異値分解すれば、\(U\)は空間方向についての特徴量、\(V\)は時間方向についての特徴量を内包した行列となり、Trace LASSOで特異値の対角行列\(\Sigma\)をスパースにすることで空間方向特徴量\(U\)と時間方向特徴量\(V\)から不要な特徴パターンを削ぎ落とし、重要な特徴パターンを抽出することが可能となるのです。
Trace LASSOも多様な場面で有効な手法であるものの、 sklearn を始めとする python の有名なモジュールには含まれていないのが難点です。
pypiやGitHubでにも良さそうなモジュールが見当たらなかったため、ここでもやはり自前でフルスクラッチしたコードで解析することとします。
細かい解説は本稿のレベルを大きく逸脱するので割愛しますが、スパース性に基づく機械学習の8.4.2項の近接勾配法で実装しています。
from sklearn.base import BaseEstimator, RegressorMixin
from sklearn.linear_model import LinearRegression
class TraceLassoRegressor(BaseEstimator, RegressorMixin):
def __init__(self, alpha = None, reshape = None, max_iter=10000, epsilon=1e-5):
self.alpha = alpha
self.reshape = reshape
self.max_iter = max_iter
self.epsilon = epsilon
self.coef_ = None
def _proximal_operator(self, matrix, threshold):
U, sigma, V = np.linalg.svd(matrix, full_matrices = False)
sigma -= threshold
sigma[sigma < 0] = 0
return U @ np.diag(sigma) @ V
def fit(self, X, y):
N, P = X.shape
y = y.reshape(-1,1)
stock0 = (X.T @ y) / N
stock1 = (X.T @ X) / N
self.eta = 1 / np.max(np.real(np.linalg.eigvals(stock1)))
initial_model = LinearRegression()
initial_model.fit(X, y)
omega = initial_model.coef_.reshape(-1,1)
for iteration_first in range(self.max_iter):
base = omega.copy()
W = omega.reshape(self.reshape)
W = self._proximal_operator(matrix = W - self.eta * (stock1 @ omega - stock0).reshape(self.reshape),
threshold = self.alpha * self.eta)
omega = W.reshape(-1,1)
if(np.linalg.norm(omega - base) < self.epsilon):
break
self.coef_ = omega.flatten()
return self
def predict(self, X):
y = np.dot(X, self.coef_)
return y
Trace LASSOはパラメータ行列\(W\)についての解析ですが、自前の TraceLassoRegressor では今までのスパース推定の手法と入出力の統一感を保つこととしました。
そのため、引数 reshape でパラメータベクトル\(\omega\)をパラメータ行列\(W\)に変換するためのreshapeサイズを指定する必要があります。
今回はセンサーの総数が26で窓内の時間遅れ総数が12なので、 reshape=(26,12) を指定します(行方向がセンサー列方向が時間遅れです)。
また出力もこれまで通り\(\omega\)で返されますので、\(W\)が必要な場合は omega.reshape(26,12) で変換して利用します。
Trace LASSOの正則化係数\(\alpha\)は、例によって sklearn.model_selection.GridSearchCV でラップすることでチューニングを行います。
from sklearn.model_selection import GridSearchCV
# TraceLassoRegressorの引数alphaの探索リストを指定
param_grid = {'alpha': np.logspace(-3,-1,10)}
# GridSearchCVでクロスバリデーション実行可能なモデルを作る
# - estimator: 学習モデルでここではTraceLassoRegressorを指定
# - param_grid: ハイパーパラメータの探索リスト
# - scoring: 個別のモデルのスコア方法にMSEを指定(他の引数は公式ドキュメント参照)
# - cv: クロスバリデーションの分割数
# - n_jobs: 並列化のジョブ数
Trace_LassoCV_model = GridSearchCV(estimator = TraceLassoRegressor(reshape = X_train_lmns.shape[1:3][::-1]), # omegaをWに戻すための行数列数
param_grid = param_grid,
scoring = 'neg_mean_squared_error',
cv = 5,
n_jobs = -1)
# 作成したクロスバリデーション実行可能なモデルにデータを投入して学習
Trace_LassoCV_model.fit(X_train_lmns_flat, y_train_lmns)
# ベストなモデルに訓練データをすべて投入して再学習
Trace_Lasso_best_model = Trace_LassoCV_model.best_estimator_
Trace_Lasso_best_model.fit(X_train_lmns_flat, y_train_lmns)
score_TL = score(y_validation_lmns, X_validation_lmns_flat @ Trace_Lasso_best_model.coef_.T)
MAE : 0.4166985507536545
RMSE : 0.5264217338683447
CORR : 0.8513433961797909
R2 : 0.7232021108789047
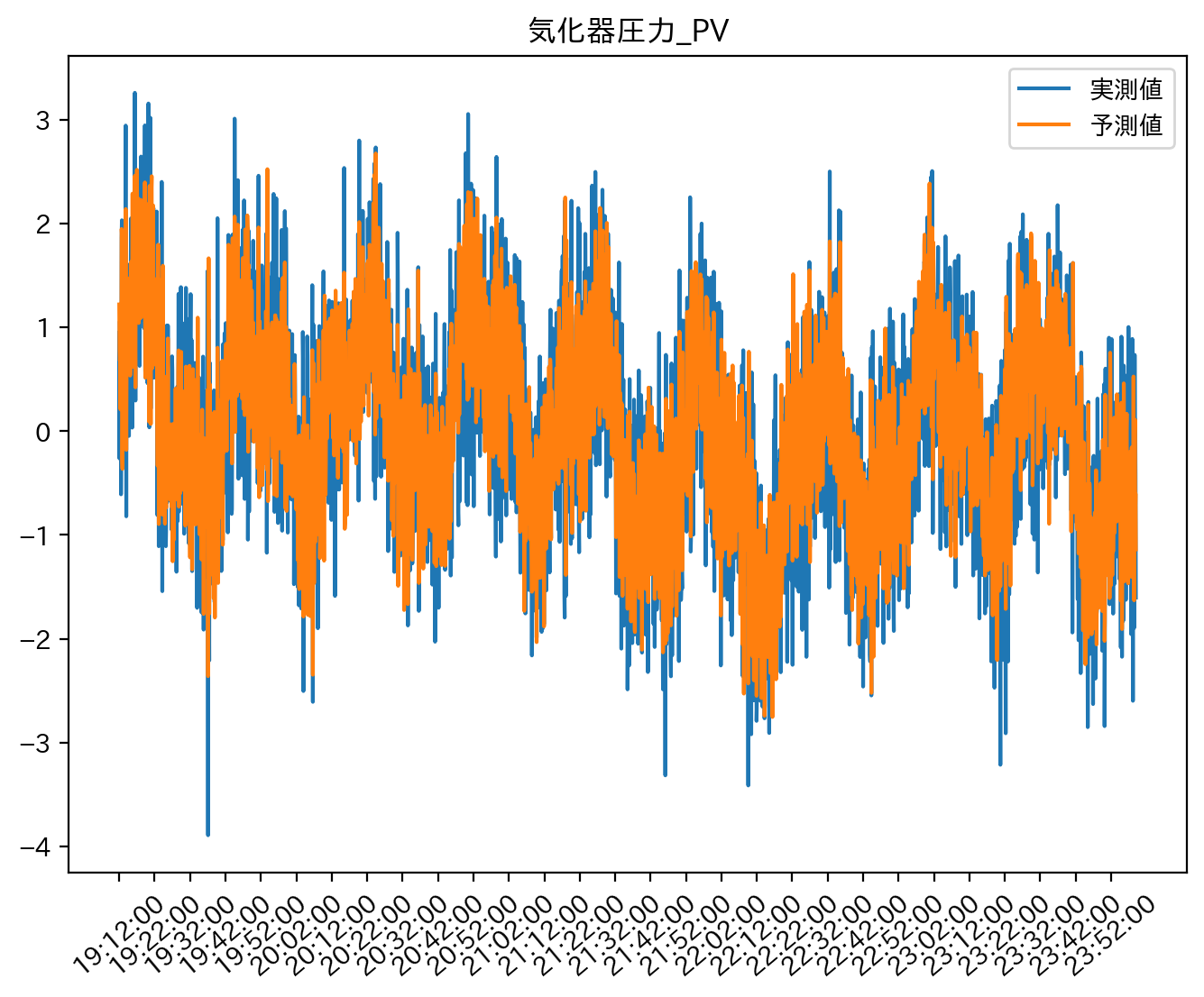
heatmap(Trace_Lasso_best_model.coef_)
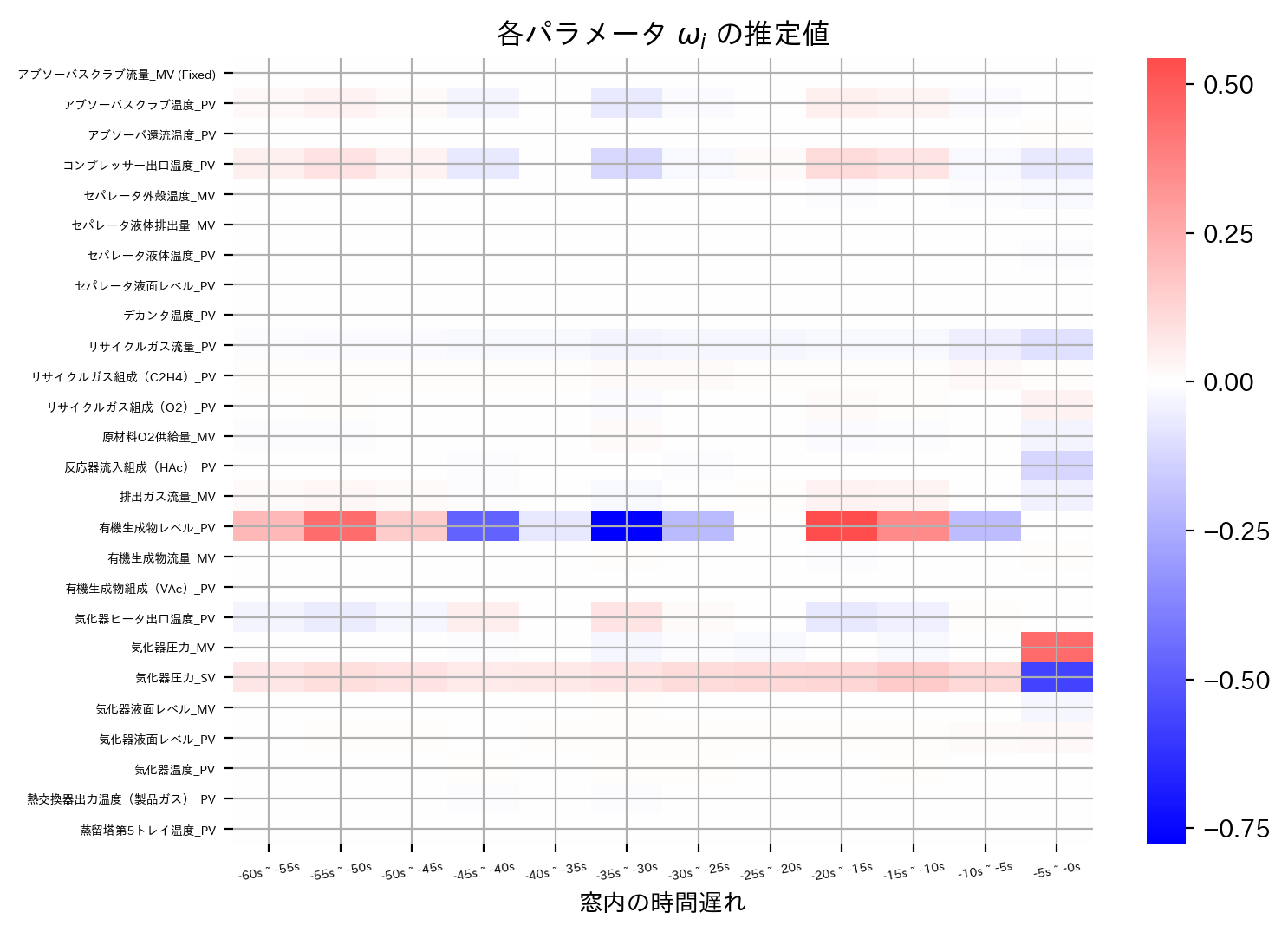
heatmap(Trace_Lasso_best_model.coef_, scale = 0.5)

Trace LASSOも低ランク性という制約を課しているので精度自体はまあまあと言ったところでしょうか。
一方でヒートマップにはTrace LASSOの良さが垣間見れ、行方向(あるいは列方向)に同じ色調パターンがいくつも点在していることが確認できます。
ここで言う色調パターンとは、正負の順序が同じでスケールが定数倍の関係にあるような色調変化を意味します。
定数倍は負の定数倍も許容できますので、正負の順序がそのままひっくり返った負正の順序も同じ色調パターンと考えて大丈夫です。
このような同じ色調パターンがいくつも点在するということは、パラメータの行列が低ランクであることと同値です。
実際、単純な線形回帰で推定したパラメータ行列のランクと、Trace LASSOで推定したパラメータ行列のランクを比較してみます。
# 単純な線形回帰での推定
from sklearn.linear_model import LinearRegression
LinearRegression_model = LinearRegression()
LinearRegression_model.fit(X_train_lmns_flat, y_train_lmns)
omega_tilde = np.abs(LinearRegression_model.coef_)
rank_LR = np.linalg.matrix_rank(LinearRegression_model.coef_.reshape(X_train_lmns.shape[1:3][::-1]))
rank_TL = np.linalg.matrix_rank(Trace_Lasso_best_model.coef_.reshape(X_train_lmns.shape[1:3][::-1]))
print(f'Rank:\tLinear Regression -> {rank_LR}\n\tTrace LASSO -> {rank_TL}')
Rank: Linear Regression -> 12
Trace LASSO -> 8
行列の最大ランクは行数or列数の小さい方と一致しますので、今回のデータでは8(時間遅れの総数)です。
従って、単純な線形回帰ではパラメータ行列はフルランクなのに対し、Trace LASSOではランクが8まで落とすことに成功しています。
そしてこれは12個存在した特異値のうち、Trace LASSOで本質的に不要な特異値を削ぎ落とした結果、重要な8つの特異値のみ抽出できていることを意味します。
今回のデータでは行方向に空間的な特徴と列方向に時間的な特徴を有するので、各特異値は対応するインデックスの時空間特徴の重要度と解釈できますので、実際にTrace LASSOで推定されたパラメータ行列を特異値分解してこのことを確認してみます。
# ベストモデルのパラメータ行列Wを特異値分解
U, sigma, V = np.linalg.svd(Trace_Lasso_best_model.coef_.reshape(26,12), full_matrices = False)
plt.figure(figsize = [8,4], dpi = 200)
plt.yscale('log')
plt.bar(np.arange(len(sigma)), sigma, color='seagreen')
plt.xticks(np.arange(len(sigma)), [f'時空間特徴 {n+1}' for n in range(len(sigma))], fontsize=8, rotation=15)
plt.ylabel('特異値 [log scale]')
plt.xlim(-0.5,len(sigma)-0.5)
plt.title('時空間特徴の特異値')
plt.grid()

縦軸が対数スケールであることに注意すると、明らかに8番目の時空間特徴以降は極端に0方向に縮小推定できていることがわかります。
このことも踏まえて一連の特異値分解の議論を思い出せば、今回のデータに対してはパラメータ行列\(W\)には重要な8つの特異値に対応した重要な特徴パターンが、行方向(\(U\)に格納)に8つ列方向(\(V\)に格納)に8つ抽出されていると考えることができますので、これを良い感じにプロットしてみます。
import matplotlib.gridspec as gridspec
plt.figure(figsize = [16,12], dpi = 200)
gs = gridspec.GridSpec(rank_TL * 2, rank_TL * 2)
for n in range(rank_TL):
plt.subplot(gs[rank_TL:, rank_TL-n-1])
plt.barh(range(X_train.shape[1]),U[:,n], color='seagreen')
plt.yticks(range(X_train.shape[1]), X_train.columns, fontsize=6)
plt.xticks(fontsize=8)
plt.ylim(X_train.shape[1]-0.5,-0.5)
plt.xlim(-1,1)
plt.xlabel(f'空間特徴 {n+1}')
plt.grid()
if(n != rank_TL-1):
plt.tick_params(labelleft=False)
for n in range(rank_TL):
plt.subplot(gs[rank_TL-n-1, rank_TL:])
plt.bar(np.arange(X_train_lmns.shape[1])+0.5, V[n], color='seagreen')
plt.xticks(np.arange(X_train_lmns.shape[1])+0.5, [f'-{(m+1)*5}s ~ -{m*5}s'for m in np.arange(X_train_lmns.shape[1])][::-1], rotation=10, fontsize=8)
plt.yticks(fontsize=8)
plt.xlim(0,X_train_lmns.shape[1])
plt.ylabel(f'時間特徴 {n+1}', rotation=75)
plt.grid()
plt.ylim(-1,1)
plt.tick_params(labelbottom=False)
plt.subplot(gs[rank_TL:, rank_TL:])
sns.heatmap(Trace_Lasso_best_model.coef_.reshape(X_train_lmns.shape[1:3][::-1]), center=0, vmin=-0.5, vmax=0.5, cmap="bwr", cbar=False)
plt.tick_params(labelleft=False)
plt.xticks(np.arange(X_train_lmns.shape[1])+0.5, [f'-{(m+1)*5}s ~ -{m*5}s'for m in np.arange(X_train_lmns.shape[1])][::-1], rotation=10, fontsize=8)
plt.yticks(np.arange(X_train.shape[1])+0.5, X_train.columns, rotation=0, fontsize=5)
plt.xlabel("窓内の時間遅れ:色調範囲[-0.5, 0.5]")
plt.ylim(X_train.shape[1],0)
plt.grid()
plt.show()
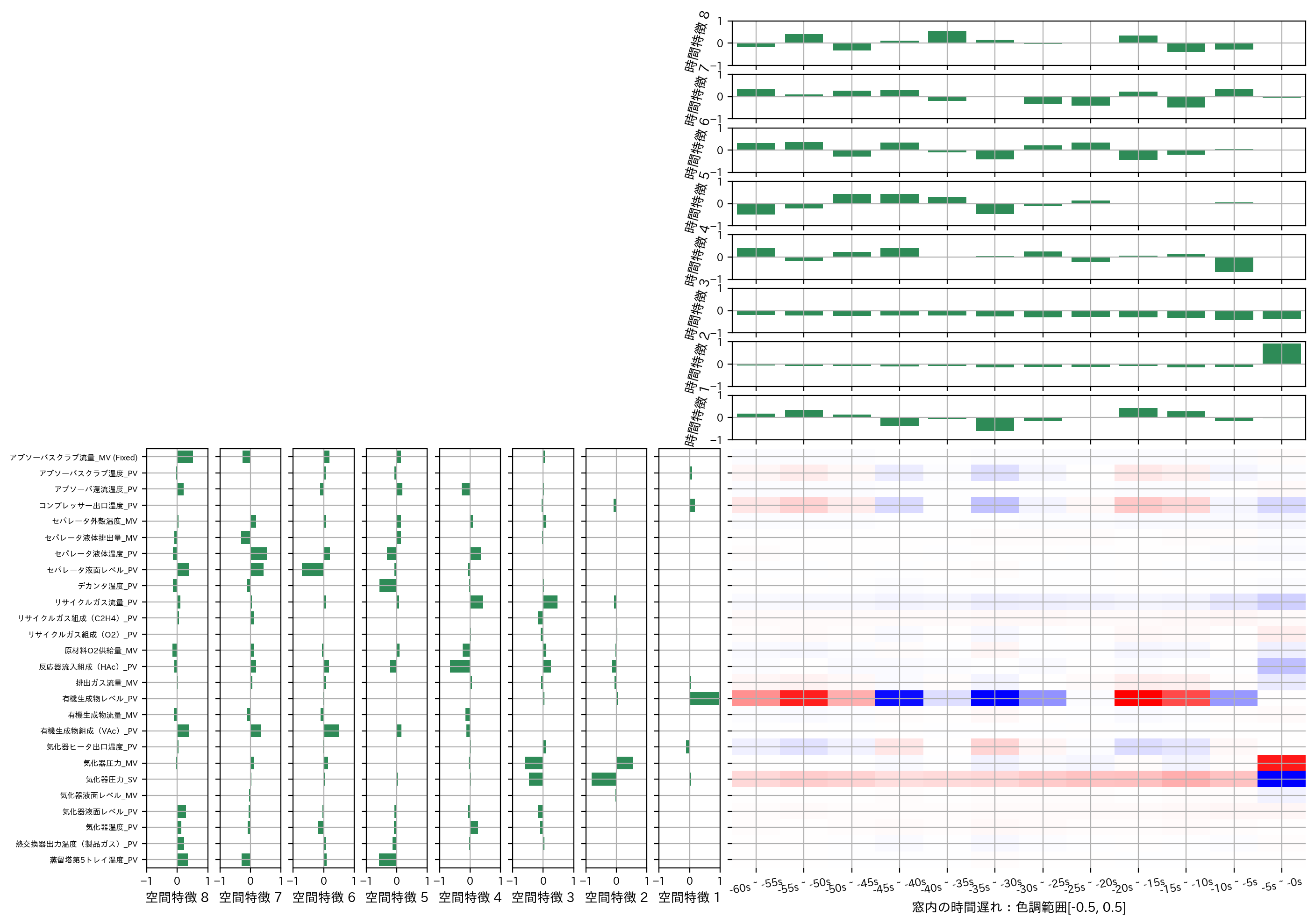
図の見方ですが、右下のヒートマップはTrace LASSOで推定されたパラメータ行列\(W\)で今まで見てきたものと同じです。
このパラメータ行列\(W\)を特異値分解して空間方向の特徴行列\(U\)と時間方向の特徴行列\(V^{\top}\)を抽出し、非ゼロとして残った特異値\(\sigma\)にそれぞれ対応した空間特徴行列\(U\)の列ベクトルを棒グラフとしてプロットしたのが左下、時間特徴行列\(V^{\top}\)の行ベクトルを棒グラフとしてプロットしたのが右上です。
すなわち、本質的に重要な特異値は5つでしたので左下は U[:,:8] を右上は V.T[:8,:] をそれぞれベクトルに分けてプロットしていることに相当します(重要な特徴がよりヒートマップに近づくようにプロットしたので順序違いはあります)。
特異値分解\(W=U\Sigma V^{\top}\)を思い出すと、\(W\)の上位8つ以外の特異値は0に縮退しているということは、言い換えれば U[:,:8] @ Sigma[:8,:8] @ V.T[:8,:] で\(W\)をほとんど再現できることを意味します。
従って左下図と右上図のこれらのベクトルは、\(W\)を表現する潜在的な時空間パターンであると解釈できるのです。
このようにTrace LASSOはパラメータ行列に内在する本質的な特徴パターンをスパースに抽出できる手法です。
この辺の詳細や関連技術は次元圧縮(前編:主成分分析)および次元圧縮(後編:その他の手法)にも掲載されていますので確認してみてください。
Graphical LASSO#
発展編2つめはGraphical LASSOと呼ばれる手法です。
ここで\(S\)は標本共分散行列で\(\Lambda\)は多変量正規分布の精度行列です(詳細は後述)。
もはや今までの流れをぶった斬るような難解な最適化問題にみえますが、実は初見殺しで理屈はTrace LASSOよりも掴みやすいと思うので、最適化問題の数理的解釈は忘れてイメージ中心で説明します。
まず前提として、Graphical LASSOは特定の回帰や分類問題のパラメータをスパースに推定する手法ではなく、多変量データ間の要因関係をスパースに推定する手法です。
そのため今まで見てきた誤差項(\(\frac{1}{2N}\|y-X\omega\|_2^2\))とは似つかないような、別の誤差項(\(\mathrm{Tr}(\Lambda S)-\log\det\Lambda\))が付与されています。
Graphical LASSOでは(中心化された)多変量データのあるサンプルベクトル\(x\)(例えばある時刻のセンサーデータベクトルなど)の生成に、次の多変量正規分布を仮定します。
ここで登場する\(\Lambda\)が先ほどの最適化問題中にあった精度行列\(\Lambda\)のことで、多変量正規分布の共分散行列の逆行列に相当します。
Graphical LASSOはデータが従う多変量正規分布の精度行列\(\Lambda\)をスパースに推定する手法なのです。
精度行列\(\Lambda\)をスパースに推定する利点ですが、実はデータが多変量正規分布に従っている場合、もし精度行列\(\Lambda\)の\((i,j)\)成分\(\Lambda_{ij}\)が0であれば、サンプルベクトル\(x\)の\(i\)番目の要素\(x_i\)に対応する変数と\(j\)番目の要素\(x_j\)に対応する変数が(条件付き)独立であることが成り立つのです。
(条件付き)独立であるとは、\(x_i\)と\(x_j\)は(\(x_i\)と\(x_j\)以外の他の\(x\)が観測されれば)お互いの生成分布はお互いに無関係であると言うことができます。
従って、Graphical LASSOで精度行列\(\Lambda\)をスパースに推定することは、0と推定された精度行列の成分に対応する変数間はお互いに直接影響し合っていないと統計的に主張できるのです。
なお、精度行列\(\Lambda\)は一般に対称行列ですので、\(\Lambda_{ij}=\Lambda_{ji}\)であることに注意してください。
例えば今回のデータでは、時間方向でサンプルした複数センサーデータの多変量時系列データと考えることができます。
これまでは 気化器圧力_PV を目的変数に指定していましたが、前述のようにGraphical LASSOでは特定のセンサーを目的変数とはしないので、ここでは従来の説明変数の最後列に 気化器圧力_PV を加えた26+1=27個の変数をもつ多変量時系列データを解析することとします(時間遅れについてはグラフの視認性に難があるため今回は考慮しないとします)。
この場合\(x\)は、ある時刻のセンサーデータを内包したセンサー総数分の27次元ベクトルとなります。
そして、\(\Lambda\)は\(x\)を生成する多変量正規分布の精度行列で\(\Lambda\in\mathbb{R}^{27\times27}\)の対称行列となります。
Graphical LASSOはこのようなデータに対して、例えばもし\(\Lambda_{2,3}=\Lambda_{3,2}=0\)であったとすれば、それは2番目のセンサー(アブソーバスクラブ温度_PV)と3番目のセンサー(アブソーバ還流温度_PV)の間に(Graphical LASSOの意味で)要因関係がないと推定できたことになります。
今までと毛色の異なるGraphical LASSOですが、実は本稿で紹介してきたAdaptive LASSO、Group LASSO、Fused LASSO、Trace LASSOと異なり、 sklearn.covariance.GraphicalLasso としてお手軽に利用できます。
さらになんとクロスバリデーションも実行してくれる sklearn.covariance.GraphicalLassoCV も存在します。
以降ではこちらの便利なモジュールを利用して、Graphical LASSOの特徴を確認していきましょう。
# 時間窓切り出し処理実行前のX_trainとy_trainを結合して、今回Graphical LASSOを適用するデータXとする
# 今まで目的変数としてきた気化器圧力_PVが最後列に挿入されていることに注意
X = pd.concat([X_train,y_train], axis=1)
X.describe()
| アブソーバスクラブ流量_MV (Fixed) | アブソーバスクラブ温度_PV | アブソーバ還流温度_PV | コンプレッサー出口温度_PV | セパレータ外殻温度_MV | ... | 気化器液面レベル_PV | 気化器温度_PV | 熱交換器出力温度(製品ガス)_PV | 蒸留塔第5トレイ温度_PV | 気化器圧力_PV | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 1.382400e+04 | 1.382400e+04 | 1.382400e+04 | 1.382400e+04 | 1.382400e+04 | ... | 1.382400e+04 | 1.382400e+04 | 1.382400e+04 | 1.382400e+04 | 1.382400e+04 |
| mean | -4.916155e-14 | -4.534182e-15 | -2.901383e-14 | -2.500058e-15 | 3.454027e-15 | ... | 3.736106e-14 | 2.263621e-14 | -6.496861e-15 | -1.118447e-15 | -1.816243e-14 |
| std | 1.000036e+00 | 1.000036e+00 | 1.000036e+00 | 1.000036e+00 | 1.000036e+00 | ... | 1.000036e+00 | 1.000036e+00 | 1.000036e+00 | 1.000036e+00 | 1.000036e+00 |
| min | -6.788798e+01 | -1.817804e+00 | -4.218247e+00 | -2.601755e+00 | -2.258724e+00 | ... | -4.765959e+00 | -4.421095e+00 | -2.300049e+00 | -3.786210e+00 | -3.912737e+00 |
| 25% | -4.910523e-03 | -9.897316e-01 | -5.995634e-01 | -8.345465e-01 | -8.018388e-01 | ... | -2.942376e-01 | -6.572871e-01 | -5.108525e-01 | -6.687863e-01 | -6.708929e-01 |
| 50% | -4.910523e-03 | -2.429429e-04 | -3.293542e-02 | 2.126674e-01 | -7.349926e-02 | ... | 1.373325e-01 | 9.486566e-04 | -2.089916e-01 | -1.168789e-02 | 2.361519e-02 |
| 75% | -4.910523e-03 | 9.956880e-01 | 5.559756e-01 | 7.702070e-01 | 6.311289e-01 | ... | 5.332820e-01 | 6.725327e-01 | 1.185327e-01 | 6.630706e-01 | 7.007588e-01 |
| max | 6.787816e+01 | 1.682316e+00 | 4.540257e+00 | 1.315360e+00 | 4.222930e+00 | ... | 3.018180e+00 | 4.166902e+00 | 4.396815e+00 | 8.184268e+00 | 3.295445e+00 |
8 rows × 27 columns
from sklearn.covariance import GraphicalLassoCV
Graphical_LassoCV_model = GraphicalLassoCV(alphas=100, cv=5, n_jobs=-1)
Graphical_LassoCV_model.fit(X.values)
# Graphical LASSOで精度行列の何%が0になったか確認
sparsity = np.mean(Graphical_LassoCV_model.precision_==0) * 100
print(f'0と推定された成分の割合: {round(sparsity, 3)}%')
0と推定された成分の割合: 52.675%
解析結果の比較方法ですが、精度行列を単純に比較するのみでは各変数に応じて精度行列の対角成分が一般に異なるので、これらのスケールを揃える必要があります。
共分散行列と相関行列との関係を思い出すと、2変数の共分散の大きさは個々の変数の分散の大きさに依存するので、単純に2つの共分散行列の成分を比較するのみでは少し不公平で、それよりは分散の大きさで各成分をスケーリングした相関行列で比較する方が自然です。
これと同様に精度行列を対角成分でスケーリングした行列として偏相関行列があり、偏相関行列の\((i,j)\)成分は\(i\)番目と\(j\)番目以外の変数の影響を考慮した場合の相関関係を意味しています。
偏相関行列の各成分を\(P_{ij}\)とすると、精度行列と偏相関行列の間には次のような関係性があります。
明らかに\(L_{ij}=0\)なら\(P_{ij}=0\)なので、このようなスケーリングを行っても行列成分のスパース性は保たれます。
実装は以下のように簡単に行えますが、このままだと偏相関行列の対角成分が\(P_{ii}=-1\)となるので実用上は対角成分のみ\(+2\)して\(P_{ii}=1\)とする場合が多いようです。
# 精度行列から偏相関行列を算出する
def partial_correlation(Lambda):
return -(Lambda / np.sqrt(np.diag(Lambda))).T / np.sqrt(np.diag(Lambda))+np.eye(len(Lambda))*2
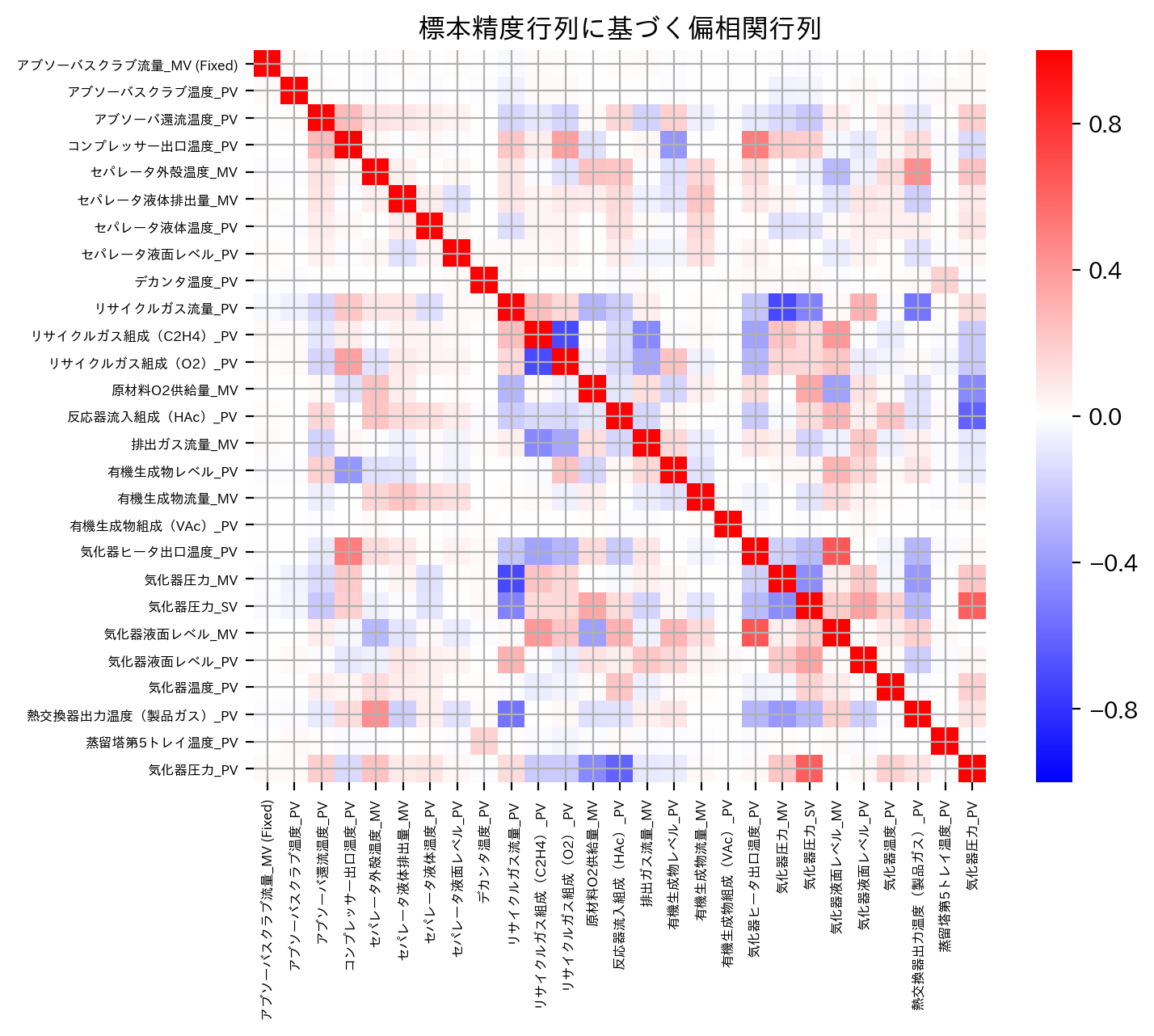
今回はGraphical LASSOの効果を確認するために、元々のデータから直接計算した標本精度行列(にもとづく偏相関行列)とGraphical LASSOによって推定された精度行列(にもとづく偏相関行列)を比較します。
なお標本精度行列は標本共分散行列の逆行列で与えられ、標本共分散行列は\(S=\frac{1}{N}X^{\top}X\)で計算できます。
# 標本精度行列の場合
S = X.values.T @ X.values / len(X.values)
plt.figure(figsize = [8,6], dpi = 200)
sns.heatmap(partial_correlation(np.linalg.inv(S)), cmap='bwr', center=0, vmin=-1, vmax=1, square=True)
plt.xticks(np.arange(X.shape[1])+0.5, X.columns, rotation=90, fontsize=6)
plt.yticks(np.arange(X.shape[1])+0.5, X.columns, rotation=0, fontsize=6)
plt.ylim(X.shape[1],0)
plt.title('標本精度行列にもとづく偏相関行列')
plt.grid()
plt.show()
# Graphical LASSOの場合
plt.figure(figsize = [8,6], dpi = 200)
sns.heatmap(partial_correlation(Graphical_LassoCV_model.precision_), cmap='bwr', center=0, vmin=-1, vmax=1, square=True)
plt.xticks(np.arange(X.shape[1])+0.5, X.columns, rotation=90, fontsize=6)
plt.yticks(np.arange(X.shape[1])+0.5, X.columns, rotation=0, fontsize=6)
plt.ylim(X.shape[1],0)
plt.title('Graphical LASSOの推定精度行列にもとづく偏相関行列')
plt.grid()
plt.show()

Graphical LASSOによって、標本精度行列(にもとづく偏相関行列)のうち重要な要因関係成分はそのままに、本質的に不要な要因関係成分は0に縮小推定できていることがわかります。
ヒートマップにして全体を確認することも非常に重要ですが、変数が多くなると視認性に欠ける場合もあるので、注目する情報に注目したネットワーク図にすると便利かもしれません。
ここでは scikit-learn のVisualizing the stock market structureを参考に、Graphical LASSOの推定結果のうち特に偏相関行列の成分の絶対値が0.3以上のものをプロットしました。
なお偏相関行列の成分の大きさは線の太さで表現し、各センサー変数はAffinity Propagationでクラスタリングされた結果に基づいて円形に並べています。
from matplotlib.collections import LineCollection
import matplotlib.colors as col
from sklearn import cluster
from scipy.stats import rankdata
_, labels = cluster.affinity_propagation(Graphical_LassoCV_model.covariance_)
n_labels = labels.max()
for l in range(n_labels + 1):
print(f'Cluster {l+1}:', ', '.join(X.columns[labels == l]))
embedding = np.zeros([2,len(labels)])
for n, s in enumerate(rankdata(labels, method='ordinal')-1):
embedding[0,n] = np.cos(2*np.pi*(s+1)/len(labels)+np.pi/2)
embedding[1,n] = np.sin(2*np.pi*(s+1)/len(labels)+np.pi/2)
plt.figure(figsize=(8,8), dpi=200)
ax = plt.axes([0., 0., 1., 1.])
plt.axis('off')
ax.set_aspect('equal')
Adj = partial_correlation(Graphical_LassoCV_model.precision_)
non_zero = np.abs(np.triu(Adj, k=1)) > 0.3 # 表示する関係性についての条件はこちら
plt.scatter(embedding[0], embedding[1], s=400, c=labels, cmap='tab10')
start_idx, end_idx = np.where(non_zero)
segments = [[embedding[:, start], embedding[:, stop]] for start, stop in zip(start_idx, end_idx)]
values = Adj[non_zero]
values_abs = np.abs(values)
lc = LineCollection(segments, zorder=0)
values_binary = np.sign(values) / 2
lc.set_array(values_binary)
lc.set_linewidths(15 * values_abs)
lc.set_cmap('bwr')
lc.set_norm(col.Normalize(vmin=-1, vmax=1))
ax.add_collection(lc)
for index, (name, label, (x, y)) in enumerate(zip(X.columns, labels, embedding.T)):
horizontalalignment = 'left' if x > 0 else 'right'
verticalalignment = 'bottom' if y > 0 else 'top'
plt.text(x, y, name, size=10,
horizontalalignment=horizontalalignment,
verticalalignment=verticalalignment,
bbox=dict(facecolor='w',
edgecolor=plt.cm.tab10(label/float(n_labels)),
linewidth=3,
alpha=.5))
plt.xlim(-1.2,1.2)
plt.ylim(-1.2,1.2)
plt.show()
Cluster 1: アブソーバスクラブ流量_MV (Fixed)
Cluster 2: アブソーバスクラブ温度_PV
Cluster 3: セパレータ外殻温度_MV, 原材料O2供給量_MV, 排出ガス流量_MV, 有機生成物流量_MV, 有機生成物組成(VAc)_PV, 熱交換器出力温度(製品ガス)_PV
Cluster 4: デカンタ温度_PV, 蒸留塔第5トレイ温度_PV
Cluster 5: アブソーバ還流温度_PV, セパレータ液体温度_PV, 反応器流入組成(HAc)_PV, 気化器圧力_MV
Cluster 6: セパレータ液体排出量_MV, セパレータ液面レベル_PV, リサイクルガス組成(C2H4)_PV, 気化器圧力_SV, 気化器液面レベル_PV, 気化器温度_PV, 気化器圧力_PV
Cluster 7: コンプレッサー出口温度_PV, リサイクルガス流量_PV, リサイクルガス組成(O2)_PV, 有機生成物レベル_PV, 気化器ヒータ出口温度_PV, 気化器液面レベル_MV
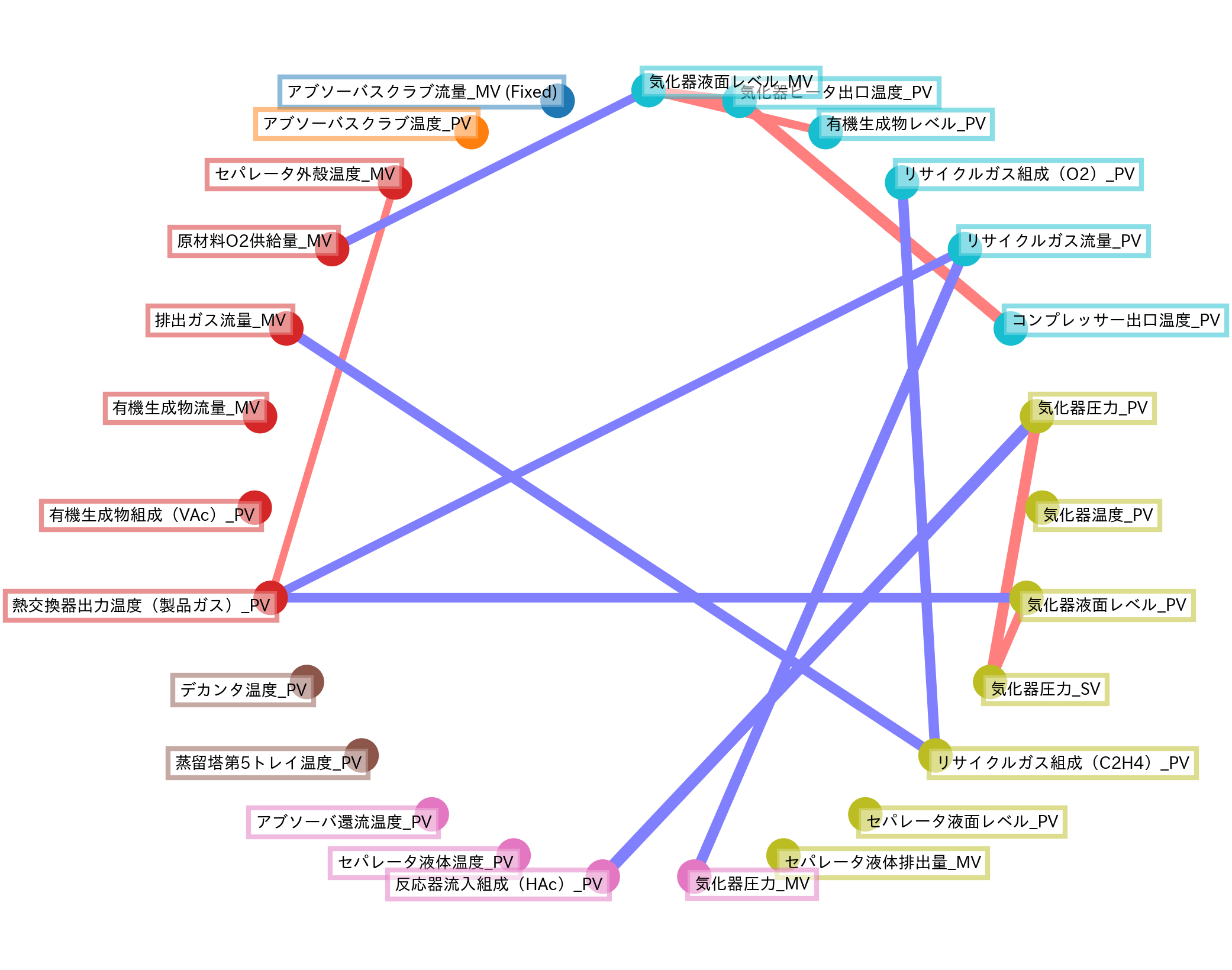
あるいは他のLASSO手法で使用した回帰問題の設定を踏襲し、これまで目的変数としてきた 気化器圧力_PV に関する要因関係成分のみプロットしてみるのも良いかもしれません。
from matplotlib.collections import LineCollection
import matplotlib.colors as col
from sklearn import cluster
from scipy.stats import rankdata
_, labels = cluster.affinity_propagation(Graphical_LassoCV_model.covariance_)
n_labels = labels.max()
for l in range(n_labels + 1):
print(f'Cluster {l+1}:', ', '.join(X.columns[labels == l]))
embedding = np.zeros([2,len(labels)])
for n, s in enumerate(rankdata(labels, method='ordinal')[:-1]-1):
embedding[0,n] = np.cos(2*np.pi*(s+1)/len(labels)+np.pi/2)
embedding[1,n] = np.sin(2*np.pi*(s+1)/len(labels)+np.pi/2)
plt.figure(figsize=(8,8), dpi=200)
ax = plt.axes([0., 0., 1., 1.])
plt.axis('off')
ax.set_aspect('equal')
Adj = partial_correlation(Graphical_LassoCV_model.precision_)
non_zero = np.zeros(Adj.shape, dtype='bool') # 表示する関係性についての条件はこちら
non_zero[:-1,-1] = True
plt.scatter(embedding[0], embedding[1], s=400, c=labels, cmap='tab10')
start_idx, end_idx = np.where(non_zero)
segments = [[embedding[:, start], embedding[:, stop]] for start, stop in zip(start_idx, end_idx)]
values = Adj[non_zero]
values_abs = np.abs(values)
lc = LineCollection(segments, zorder=0)
values_binary = np.sign(values) / 2
lc.set_array(values_binary)
lc.set_linewidths(15 * values_abs)
lc.set_cmap('bwr')
lc.set_norm(col.Normalize(vmin=-1, vmax=1))
ax.add_collection(lc)
for index, (name, label, (x, y)) in enumerate(zip(X.columns, labels, embedding.T)):
horizontalalignment = 'left' if x > 0 else 'right'
verticalalignment = 'bottom' if y > 0 else 'top'
plt.text(x, y, name, size=10,
horizontalalignment=horizontalalignment,
verticalalignment=verticalalignment,
bbox=dict(facecolor='w',
edgecolor=plt.cm.tab10(label/float(n_labels)),
linewidth=3,
alpha=.5))
plt.xlim(-1.2,1.2)
plt.ylim(-1.2,1.2)
plt.show()
Cluster 1: アブソーバスクラブ流量_MV (Fixed)
Cluster 2: アブソーバスクラブ温度_PV
Cluster 3: セパレータ外殻温度_MV, 原材料O2供給量_MV, 排出ガス流量_MV, 有機生成物流量_MV, 有機生成物組成(VAc)_PV, 熱交換器出力温度(製品ガス)_PV
Cluster 4: デカンタ温度_PV, 蒸留塔第5トレイ温度_PV
Cluster 5: アブソーバ還流温度_PV, セパレータ液体温度_PV, 反応器流入組成(HAc)_PV, 気化器圧力_MV
Cluster 6: セパレータ液体排出量_MV, セパレータ液面レベル_PV, リサイクルガス組成(C2H4)_PV, 気化器圧力_SV, 気化器液面レベル_PV, 気化器温度_PV, 気化器圧力_PV
Cluster 7: コンプレッサー出口温度_PV, リサイクルガス流量_PV, リサイクルガス組成(O2)_PV, 有機生成物レベル_PV, 気化器ヒータ出口温度_PV, 気化器液面レベル_MV
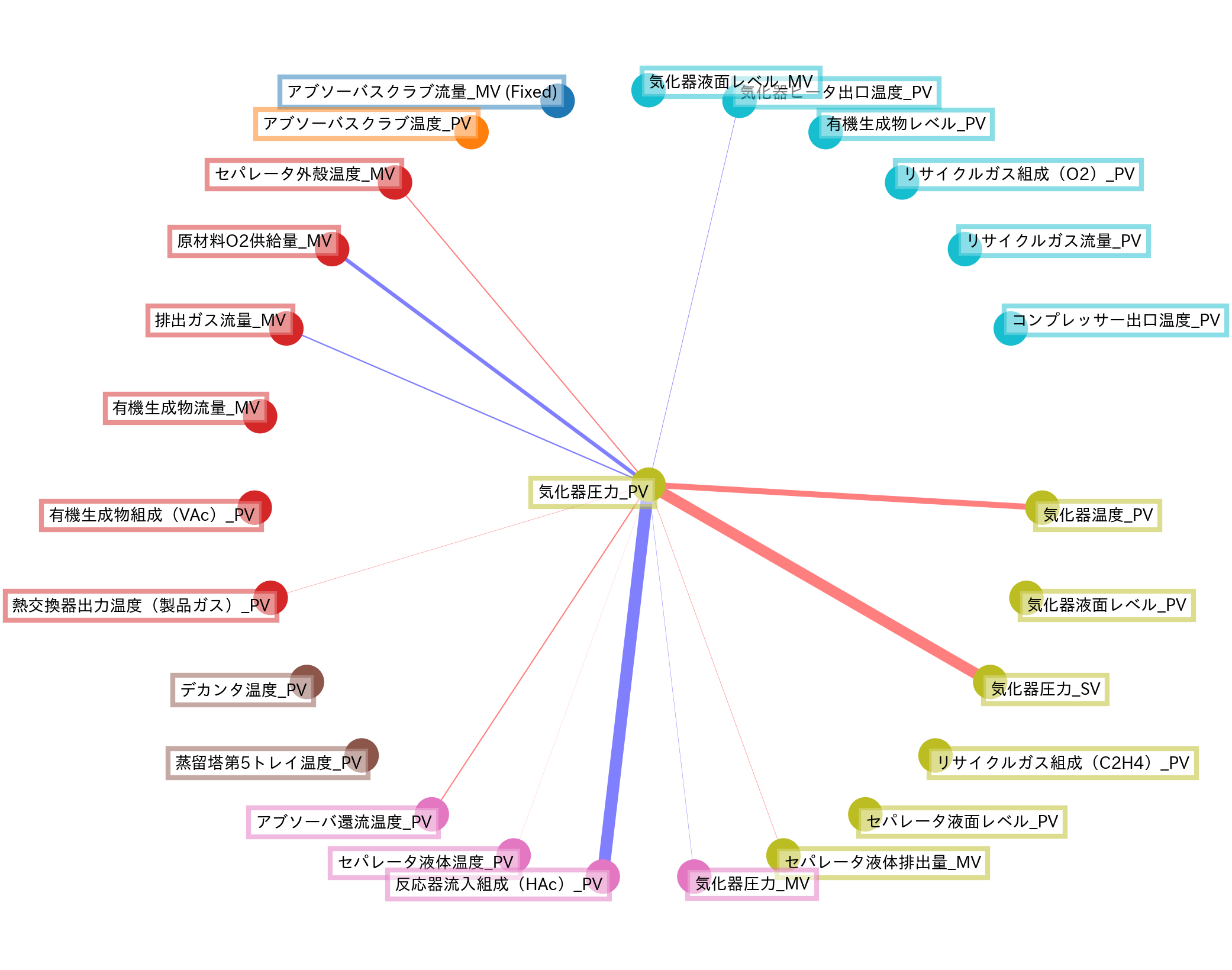
Graphical LASSOの視点で、目的変数 気化器圧力_PV に対する各説明変数の(同時刻における)要因関係を可視化できました。
Graphical LASSOは直接回帰問題を解くような手法ではありませんが、例えばここで求めた要因関係の結果を所望の回帰問題に反映して間接的に推定精度の向上に寄与することも考えられます。
このようにGraphical LASSOでは、変数間に内在する要因関係をスパースに推定する手法です。
さらなる発展として、イノベーションセンターテクノロジー部門ではGraphical LASSOの要因構造に潜在変数と確率分布を導入したLatent Structured Graphical LASSOなども研究開発しています。
小括#
本稿ではスパースモデリング(基本編)やスパースモデリング(応用編)に引き続き、スパースモデリングのさまざまな発展手法について紹介しました。
なかなか技術的難易度の高い箇所もあったかもしれませんが、正則化項の形状に応じて多種多様なスパース性を誘導することができる、スパースモデリングは奥が深くて自由度の高い世界なんだと感じていただければ幸いです。
一方で本稿で紹介したスパースモデリング手法も例に違わず、スパースモデリング(基本編)のLASSOなどで詳しく確認したように、ノルムで表現される単位球がそれぞれの手法の意味で尖っているのでそれぞれ固有の特徴的なスパース性が誘導されています。
このことを逆に言えば、ノルムで表現される単位球に良い感じに尖っている箇所を設計することで、新しい特徴をもった独自のスパースモデリング手法を生み出せることを示唆しています。
スパース性に基づく機械学習の10章では、この幾何的な直感をアトミックノルムを用いて詳しく解説してくれていますので、興味のある方はぜひ読んでみてください。

