パネルデータの作成と分析

パネルデータの作成と分析#

社会科学の分野で広く利用されているパネルデータ(英: panel data)とその作成方法の例および固定効果モデルによる分析の例について説明します。

パネルデータとは、複数期間に渡って複数の同じユニット(個人、地域、組織などのデータ上の分析単位)を”追跡できる形で”観察した時系列横断データのことです。以下の図のように時系列データとクロスセクション(横断面)データを組み合わせたものと表現されることもあります。

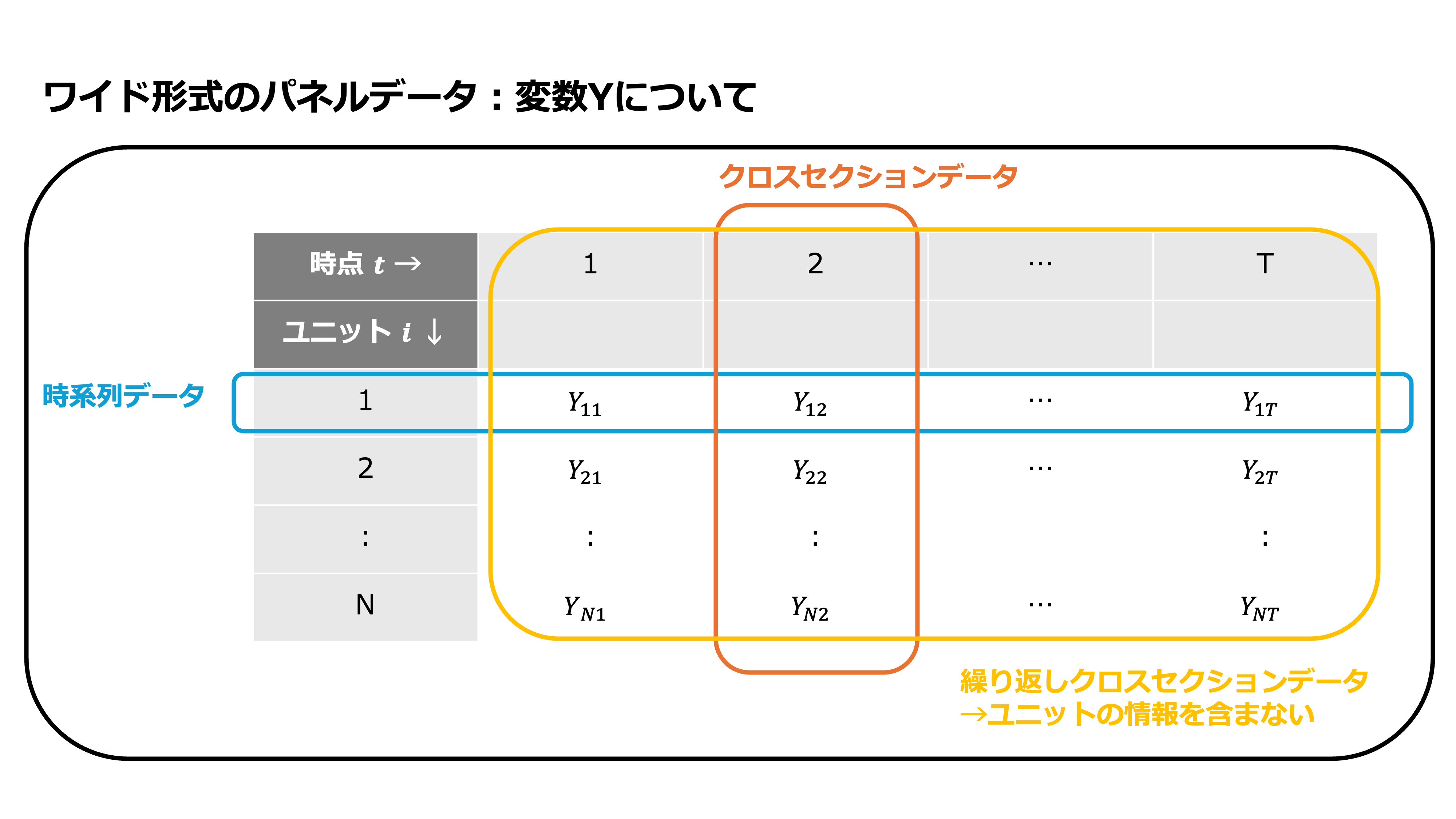
panel_data_wide_format

パネルデータを使うことの利点の1つに固定効果モデルの利用が可能になるという点があります。固定効果モデルを使うことによって欠落変数バイアスの一部に対処でき、この利点のために、パネルデータは広く利用されています。パネルデータを用意し、固定効果モデルを使うことで、主体に特有の、時間を通じて不変であるような、観察されていない変数の影響(欠落変数バイアス)をコントロールできます。

本稿では、パネルデータの作成方法や形式について主に説明します。固定効果モデルについては、linearmodels による実装方法の説明のみとどめ、固定効果モデルとその推定量についての理論的な詳細は省略するため、別の文献を参照してください。

注意

  • 本稿では計量経済学における用語にもとづいて説明します

    • パネルデータは、経時データ(英: longitudinal data)と呼ばれることもあります

  • 本稿の実行例では、linearmodels ライブラリv6.0を利用しており、解説もこのバージョンでの実装にもとづいて行います

# !pip install linearmodels==6.0

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np

import statsmodels.api as sm

import linearmodels
from linearmodels.datasets import wage_panel
from linearmodels.panel.data import PanelData

# 警告を非表示にする
import warnings

warnings.simplefilter("ignore", FutureWarning)

# pandasの表示設定
pd.set_option("display.max_columns", None)  # データフレーム内のすべての列を表示する
pd.set_option(
    "display.max_colwidth", None
)  # 列の最大幅を無制限にして、テキストの切り捨てを防ぐ

# matplotlibでは日本語にデフォルトで対応していないので、日本語対応フォントを読み込む
# plt.rcParams['font.family'] = 'BIZ UDGothic' # Windows
plt.rcParams["font.family"] = "Hiragino Maru Gothic Pro"  # Mac

# 使えるフォント一覧は以下のコードで取得できます。
# import matplotlib.font_manager
# [f.name for f in matplotlib.font_manager.fontManager.ttflist]

パネルデータとはなにか？#

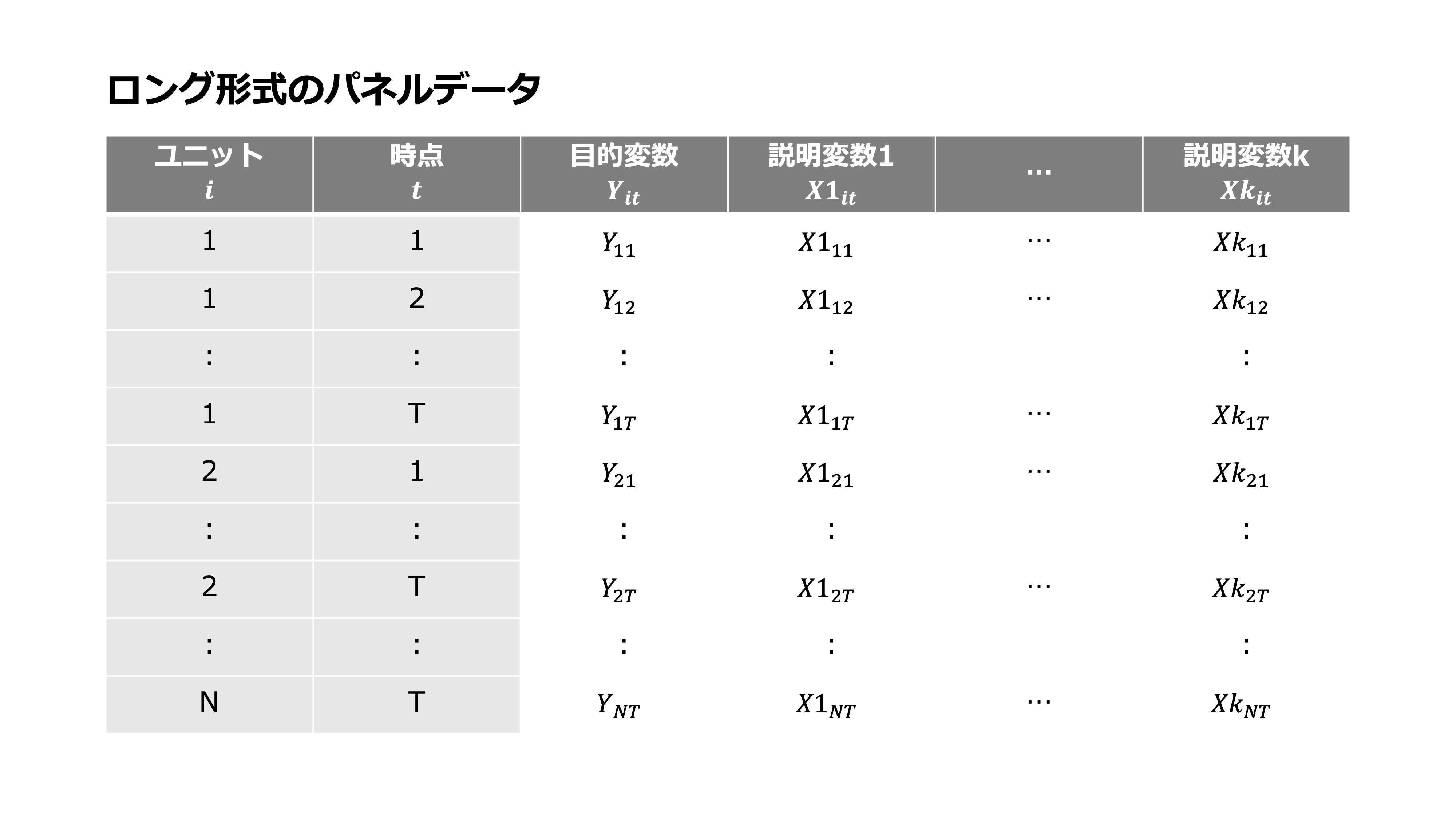
パネルデータとは、複数期間に渡って複数の同じユニットを”追跡できる形で”観察した時系列横断データです。したがって、パネルデータにおいて観察されたデータを特定するためには、ユニットに関する情報と時点に関する情報が必要です。本稿では、ユニットに関する添字を\(i=1,2,...,N\)とし、時点に関する添字を\(t=1,2,...,T\)として、ユニット\(i\)に関する時点\(t\)での目的変数を\(Y_{it}\)とし、観測された説明変数を\(X_{it}\)として、変数番号を\(k=1,2,...,K\)として\(Xk_{it}\)と表します。

paneldata_long

使用するデータ#

具体例として、F. Vella and M. Verbeek (1998)[1]のデータをもとに説明します。このデータ分析の目的は、パネルデータを用いて労働組合への参加が賃金に与える影響を分析することです。

はじめにデータセットに含まれる変数について確認します。

from linearmodels.datasets import wage_panel

print(wage_panel.DESCR)

df = wage_panel.load()

F. Vella and M. Verbeek (1998), "Whose Wages Do Unions Raise? A Dynamic Model
of Unionism and Wage Rate Determination for Young Men," Journal of Applied
Econometrics 13, 163-183.

nr                       person identifier
year                     1980 to 1987
black                    =1 if black
exper                    labor market experience
hisp                     =1 if Hispanic
hours                    annual hours worked
married                  =1 if married
educ                     years of schooling
union                    =1 if in union
lwage                    log(wage)
expersq                  exper^2
occupation               Occupation code

このデータセットには、以下の10変数が含まれています。今回は労働組合への加入が賃金に影響を及ぼすかを知りたいため、目的変数としては賃金に、説明変数としては労働組合への参加ダミーに着目します。

変数

説明

nr

個人の識別子

year

1980年から1987年

black

黒人なら1

exper

就労年数

hisp

ヒスパニックなら1

hours

労働時間

married

結婚しているなら1

educ

教育年数

union

労働組合に入っているなら1

今回興味がある説明変数

lwage

賃金の対数値

目的変数

expersq

exper(就労年数)の2乗

occupation

職業コード

データの中身を確認します。

df.head(16)
nr year black exper hisp hours married educ union lwage expersq occupation
0 13 1980 0 1 0 2672 0 14 0 1.197540 1 9
1 13 1981 0 2 0 2320 0 14 1 1.853060 4 9
2 13 1982 0 3 0 2940 0 14 0 1.344462 9 9
3 13 1983 0 4 0 2960 0 14 0 1.433213 16 9
4 13 1984 0 5 0 3071 0 14 0 1.568125 25 5
5 13 1985 0 6 0 2864 0 14 0 1.699891 36 2
6 13 1986 0 7 0 2994 0 14 0 -0.720263 49 2
7 13 1987 0 8 0 2640 0 14 0 1.669188 64 2
8 17 1980 0 4 0 2484 0 13 0 1.675962 16 2
9 17 1981 0 5 0 2804 0 13 0 1.518398 25 2
10 17 1982 0 6 0 2530 0 13 0 1.559191 36 2
11 17 1983 0 7 0 2340 0 13 0 1.725410 49 2
12 17 1984 0 8 0 2486 0 13 0 1.622022 64 2
13 17 1985 0 9 0 2164 0 13 0 1.608588 81 7
14 17 1986 0 10 0 2749 0 13 0 1.572385 100 7
15 17 1987 0 11 0 2476 0 13 0 1.820334 121 5

これよりたとえば、識別子nrが13の個人は1981年に労働組合に参加していて、それ以外の年は労働組合に参加していないことがわかります。

欠損値の確認#

linearmodels の PanelData オブジェクトを使うことで、各時点のユニットごとの欠損値を簡単に確認できます。PanelData を使うためには、外側のインデックスがユニットで、内側のインデックスが時間インデックスである MultiIndex DataFrameの必要があります。

df_mi = df.set_index(["nr", "year"])  # multi-indexを設定

from linearmodels.panel.data import PanelData

PanelData(df_mi).isnull

nr     year
13     1980    False
       1981    False
       1982    False
       1983    False
       1984    False
               ...  
12548  1983    False
       1984    False
       1985    False
       1986    False
       1987    False
Length: 4360, dtype: bool

PanelData オブジェクトの isnull はプロパティとして実装されているため、通常のPandasの isnull() のように括弧をつけずに呼び出すことに注意してください。

# まとめて確認する
PanelData(df_mi).isnull.any()

False

列ごとに欠損値を見たいときは、pandasデータフレームに対して以下の操作を行います。

df_mi.isnull().any()

black         False
exper         False
hisp          False
hours         False
married       False
educ          False
union         False
lwage         False
expersq       False
occupation    False
dtype: bool

wage_panelのデータセットには欠損値が生じていないことがわかりました。欠損値が生じている場合は、次に説明する不揃いなパネルデータになっている可能性に注意が必要です。

不揃いなパネルデータ#

次に、ユニットごとに観測期間が異なっているかどうかを確認します。ユニットごとに観測期間が異なっているようなデータセットは、不揃いなパネルデータ(英: unblanced panel data)と呼ばれます。実際のパネルデータも不揃いであることが多くあります。

不揃いなパネルデータでも固定効果モデルによる分析を行うことができますが、そのためにはユニットが脱落している理由が説明変数を条件付けたうえでランダム(無作為)であるであるという仮定が必要になります。たとえば、今回の労働組合と賃金の分析で、調査からの脱落が退職によって生じた場合を例に考えます。このとき、労働組合に参加していないため業績を理由に退職させられる人と、労働組合に参加していたために業績に応じて賃金が下がるが退職しなかった人がいるという状況を考えると、業績の情報がデータに含まれていない場合、労働組合に参加すると賃金が下がるという結果だけが観察されてしまい、無作為な脱落とは言えません。したがって、固定効果モデルによる推定をする場合でも、系統的な脱落が生じていないかを確認する必要があります。

たとえば以下のように不揃いなパネルデータかどうかを確認できます。

# パネルデータを確認する
# 特定の行を削除して実験する (例として2番目と89番目の行を削除)
df_dropped = df_mi.drop([df_mi.index[1], df_mi.index[88]])

# 欠損させたユニットと年の表示
print("次のデータを欠損させる", df_dropped.index[1], df_dropped.index[88])

次のデータを欠損させる (13, 1982) (193, 1982)

# すべてのnr (識別子) を取得
nr_values = df_dropped.index.get_level_values("nr").unique()

# すべてのyear (年) の範囲を取得
year_min = df_dropped.index.get_level_values("year").min()
year_max = df_dropped.index.get_level_values("year").max()
year_range = range(year_min, year_max + 1)

# nrとyearのすべての組み合わせを作成
complete_index = pd.MultiIndex.from_product(
    [nr_values, year_range], names=["nr", "year"]
)

# 欠損している(nr, year)の組み合わせを抽出
# complete_index から、実際のデータに存在するインデックスの差分を取得
missing_index = complete_index.difference(df_dropped.index)
missing_index

MultiIndex([( 13, 1981),
            (193, 1980)],
           names=['nr', 'year'])

サンプルサイズの確認#

次にこのデータにどのくらいの時点とユニットが含まれているか確認します。linearmodels の PanelData オブジェクトを使うことで、マルチインデックスをパネルデータとして扱い、変数、時点、ユニットにわけてその数を表示することができます。このデータセットには、10変数分の8年に渡る545人の若年男性労働者についてのデータが含まれています。これを確認します。

PanelData(df_mi).shape

(10, 8, 545)

ただし、不揃いなパネルデータでも同様に表示されるため、注意が必要です。不揃いなパネルデータの節で使用したデータを使って確認してみます。

PanelData(df_dropped).shape

(10, 8, 545)

したがって、データのサイズそのものも確認する必要があります。

先ほどこのパネルデータが不揃いでないことを確認したため、これは、\(N=545\)、\(T=8\)のパネルデータで、\(N \times T=4360\) 行のデータが含まれています。これはたとえば以下のように確認できます。

df_mi.shape

(4360, 10)

不揃いなパネルデータでも確認してみます。

df_dropped.shape

(4358, 10)

パネルデータにおけるデータ形式：ロング形式とワイド形式#

パネルデータでよく使われるデータ形式には、ロング形式(英: long format)とワイド形式(英: wide format)の2つがあります。この章では、ロング形式とワイド形式のデータについて説明し、相互に変換を行う方法の説明と実装を行います。

ロング形式は、列に個々の変数が記録され、行に1つの観測が記録される形式です。

ワイド形式は、セルの値はすべて1つの変数について記録された値であり、行にユニット、列に時間をとるデータ形式です。

ロング形式の方が計算機を利用したデータ分析に適していることに加え、ロング形式からワイド形式の変換は簡単にできることから、データの蓄積や利用の際は、ロング形式を前提としていることが多くあります。一方で人間に対する理解のしやすさでは、ワイド形式に軍配があがるため、目的によってデータ形式を変換する必要があります。

ロング形式の特徴#

パネルデータにおけるロング形式は、行方向がある時点ある主体における1つの観測を表し、列方向が変数を表します。新しい観測(データ)を行方向に追加するデータ構造を持ちます。ロング形式は縦持ちと呼ばれることもあります。縦持ちと呼ばれることからも分かる通り、縦方向(行方向)に長いデータ形式です。

テーブルデータは、行方向へのデータの追加が容易なため、多くのライブラリやソフトウェアで前提とされているデータ形式です。

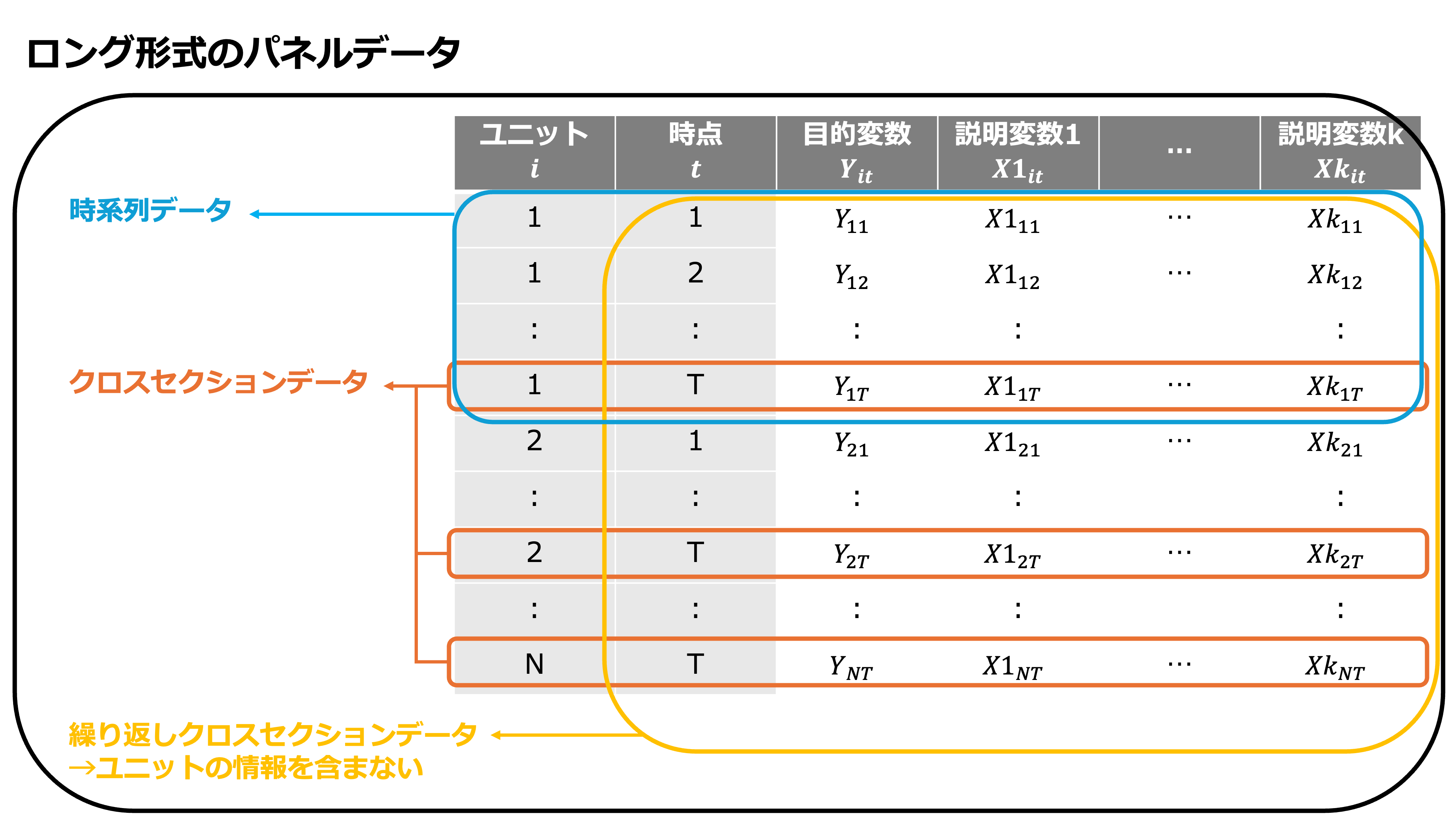
paneldata_long_format

ワイド形式の特徴#

パネルデータにおけるワイド形式は、行と列にユニットと時間をとり、セルの値はすべて1つの変数についての値です。パネルデータでは、行にユニット、列に時間のデータを保持することが多いです。ワイド形式は横持ちと呼ばれることもあります。横持ちと呼ばれることからも分かる通り、横方向(列方向)に長いデータ形式です。

ワイド形式は、一覧性が高いために人間に理解しやすいと言われることが多い一方で、テーブル構造の変更なしにはデータの追加が困難であることや、複数の変数を1つのデータフレームにまとめづらいことからデータの蓄積に向いておらず、加えて、データ分析で使用されるライブラリやソフトウェアでもロング形式での処理を前提としていることが多いために、計算機による分析には向いていません。

paneldata_wide

データ形式の変換#

ロング形式からワイド形式への展開#

先述した通り、ロング形式のままでは人間にとって見づらいことが多いため、レポーティングや可視化のためにワイド形式に変換することがあります。ここでは pandas の pivot メソッドを使って変換を行います。

# 例として労働組合への参加ダミーをワイド形式に変換
union_wide = df.pivot(index="nr", columns="year", values="union")
union_wide.head(16)
year 1980 1981 1982 1983 1984 1985 1986 1987
nr
13 0 1 0 0 0 0 0 0
17 0 0 0 0 0 0 0 0
18 0 0 0 0 0 0 0 0
45 1 1 0 0 0 0 0 0
110 1 0 0 0 0 0 0 0
120 0 0 0 0 0 0 0 0
126 0 0 0 0 0 0 0 0
150 0 0 0 0 0 0 0 1
162 1 0 0 0 0 0 0 0
166 1 1 1 1 1 0 0 0
189 0 0 0 0 0 0 0 0
193 0 0 0 0 0 0 0 0
209 0 0 0 0 0 0 0 0
212 0 0 1 0 0 0 0 1
218 0 0 0 0 0 0 0 0
243 0 0 0 0 0 0 0 0

たとえば、上記のようにunion(労働組合参加ダミー)をワイド形式で表示すると、だれがどの年に労働組合に参加しているかの様子がわかります。ここでは16行(16人分)表示しましたが、ロング形式の場合は、以下のように2人分を表示することしかできません。1つの変数に着目する場合にはワイド形式のほうが一覧性が高いことがわかります。

df.head(16)
nr year black exper hisp hours married educ union lwage expersq occupation
0 13 1980 0 1 0 2672 0 14 0 1.197540 1 9
1 13 1981 0 2 0 2320 0 14 1 1.853060 4 9
2 13 1982 0 3 0 2940 0 14 0 1.344462 9 9
3 13 1983 0 4 0 2960 0 14 0 1.433213 16 9
4 13 1984 0 5 0 3071 0 14 0 1.568125 25 5
5 13 1985 0 6 0 2864 0 14 0 1.699891 36 2
6 13 1986 0 7 0 2994 0 14 0 -0.720263 49 2
7 13 1987 0 8 0 2640 0 14 0 1.669188 64 2
8 17 1980 0 4 0 2484 0 13 0 1.675962 16 2
9 17 1981 0 5 0 2804 0 13 0 1.518398 25 2
10 17 1982 0 6 0 2530 0 13 0 1.559191 36 2
11 17 1983 0 7 0 2340 0 13 0 1.725410 49 2
12 17 1984 0 8 0 2486 0 13 0 1.622022 64 2
13 17 1985 0 9 0 2164 0 13 0 1.608588 81 7
14 17 1986 0 10 0 2749 0 13 0 1.572385 100 7
15 17 1987 0 11 0 2476 0 13 0 1.820334 121 5

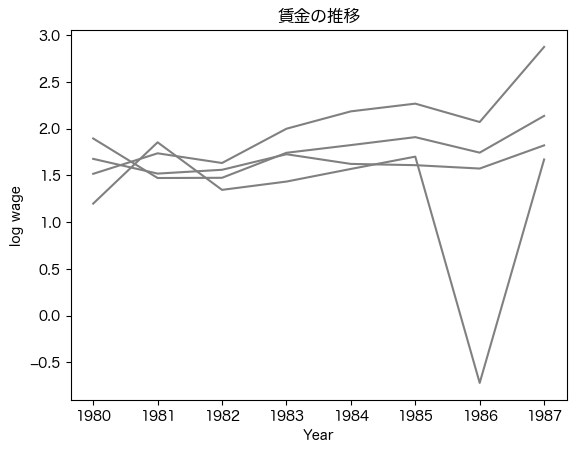
可視化する際にもワイド形式は有効です。ここでは例として賃金の推移を可視化します。

# 賃金の変数も同様にワイド形式に変換
wage_wide = df.pivot(index="nr", columns="year", values="lwage")
wage_wide.head(16)
year 1980 1981 1982 1983 1984 1985 1986 1987
nr
13 1.197540 1.853060 1.344462 1.433213 1.568125 1.699891 -0.720263 1.669188
17 1.675962 1.518398 1.559191 1.725410 1.622022 1.608588 1.572385 1.820334
18 1.515963 1.735379 1.631744 1.998229 2.184014 2.266662 2.069944 2.873161
45 1.894115 1.471159 1.473498 1.740914 1.823214 1.908273 1.742447 2.135689
110 1.948775 1.962259 1.963297 2.202516 2.134954 2.125823 1.991017 2.112393
120 0.258555 1.319972 1.462085 1.320287 1.703647 1.445803 1.806364 2.148120
126 1.737285 1.989601 2.189917 1.855463 1.922438 2.061024 1.782202 2.414682
150 1.208735 1.194040 1.170441 1.097965 0.765816 1.119026 1.119367 0.831459
162 0.502470 1.064912 1.189498 1.539889 1.598286 1.737321 1.988456 2.158679
166 1.005294 0.937687 1.367488 1.378009 1.170184 1.728221 1.709865 1.851075
189 1.130545 0.836248 1.467360 1.071484 1.445920 1.685116 1.686175 1.755130
193 1.565692 2.493875 1.822662 2.380336 2.217129 2.272032 2.353799 2.429450
209 1.918003 0.765408 1.978185 1.948554 2.037026 1.902575 1.972604 2.186982
212 1.784472 2.179983 1.963865 2.044933 2.012861 2.096986 2.143966 2.241284
218 2.013313 1.962152 2.275641 2.194918 2.428337 2.723037 2.966396 3.065052
243 1.564181 1.683546 1.690503 1.660872 1.698051 1.671768 1.635718 1.786971 
# 可視化
# 時系列に沿った個人(nr)ごとの賃金をプロット
import matplotlib.pyplot as plt

fig, ax = plt.subplots()

# 転置して最初の4人分の賃金推移をプロット
wage_wide[:4].T.plot(ax=ax, legend=False, color="gray", alpha=1)

# x軸とy軸のラベルを設定
ax.set_xlabel("Year")
ax.set_ylabel("log wage")

# グラフのタイトル
ax.set_title("賃金の推移")


# グラフの表示
plt.show()
../_images/e90708e0ece0fe018705172ca473ddd9cadd4c6d8248c9131c14b2d2f68072fe.png

ワイド形式をロング形式に変換し統合する方法#

ワイド形式をロング形式に変換し統合することは、ライブラリやソフトウェアを利用して分析する場合に必要となることが多いです。このような作業は、データの収集を表計算ソフトなどで行っている場合に起こりやすいです。

ワイド形式では、1つのデータフレームに1つの変数を表現することしかできないため、他の変数については別のデータフレームとして提供される場合が多いです。つまり、他の変数のデータは、別のファイルであったり、スプレッドシートであれば、別のシートに記載されていることが多いです。したがって、ワイド形式のデータを分析に使用する場合には、それぞれの変数について、ロング形式に変換したうえでデータフレームにまとめることで、1つのロング形式のデータフレームとしてデータ分析に使用することができるようになります。

以下に melt メソッドを利用したワイド形式からロング形式への変換の例を載せます。

# 労働組合参加ダミーのデータをロング形式に変換
union_long = (
    union_wide.reset_index()
    .melt(id_vars="nr", var_name="year", value_name="union", ignore_index=False)
    .reset_index(drop=True)
)

union_long
nr year union
0 13 1980 0
1 17 1980 0
2 18 1980 0
3 45 1980 1
4 110 1980 1
... ... ... ...
4355 12451 1987 0
4356 12477 1987 1
4357 12500 1987 0
4358 12534 1987 0
4359 12548 1987 1

4360 rows × 3 columns

# 賃金のデータも同様にロング形式に変換
wage_long = (
    wage_wide.reset_index()
    .melt(id_vars="nr", var_name="year", value_name="lwage", ignore_index=False)
    .reset_index(drop=True)
)

wage_long
nr year lwage
0 13 1980 1.197540
1 17 1980 1.675962
2 18 1980 1.515963
3 45 1980 1.894115
4 110 1980 1.948775
... ... ... ...
4355 12451 1987 1.876827
4356 12477 1987 2.202487
4357 12500 1987 1.306740
4358 12534 1987 2.342917
4359 12548 1987 1.466543

4360 rows × 3 columns

# 労働組合参加ダミーのデータと賃金のデータを統合する
# パネルデータのindexはユニットの識別子と時点の組み合わせになるので、それをキーにして統合する
df_long = pd.merge(union_long, wage_long, on=["nr", "year"])
df_long
nr year union lwage
0 13 1980 0 1.197540
1 17 1980 0 1.675962
2 18 1980 0 1.515963
3 45 1980 1 1.894115
4 110 1980 1 1.948775
... ... ... ... ...
4355 12451 1987 0 1.876827
4356 12477 1987 1 2.202487
4357 12500 1987 0 1.306740
4358 12534 1987 0 2.342917
4359 12548 1987 1 1.466543

4360 rows × 4 columns

パネルデータと時系列データ、クロスセクションデータとの関係#

パネルデータについて理解を深めるために他のデータ構造の例示とパネルデータとの関係について説明します。パネルデータは、時系列データとクロスセクションデータ(横断面データ)を組み合わせたものであると説明されることが多いため、ここでは、時系列データとクロスセクションデータの説明と例示によってパネルデータについての理解を深めます。そして、これらのデータセットを複数集めたときにパネルデータとして扱うための処理の一例を実行します。

またパネルデータと似ているものの異なる構造として、繰り返しクロスセクションデータやプールされたクロスセクションデータと呼ばれる、ユニットを”追跡できない”形で、複数時点において観察したデータ形式があります。繰り返しクロスセクションデータについてもパネルデータとのちがいや、このような形式の場合にも擬似的にパネルデータとして扱うための工夫を説明します。

データ構造の説明#

時系列データ#

時系列データは、ある1標本のデータを複数時点で観察したデータです。たとえば、本サイトごちきかで使用しているvamsimのデータや愛知県の2000年から2020年までの人口推移データ、wage_panelデータセットにおける識別子nrが13の個人だけのデータなどがこれに当てはまります。

# wage_panelデータセットにおける個人の識別子13の時系列データ
df_mi.query("nr == 13")

# multi-indexのデータフレームにおいて、データを抽出する方法はいくつか存在します。たとえば、以下でも同じ結果が得られます。
# 上記のようにqueryを使うことで、multiindexでもそうでなくても同じ書き方で動作します。
# df_mi.loc[(13, slice(None)), :]
# df_mi[df_mi.index.get_level_values(0) == 13]

# 以下のように、linearmodelsのPanelDataを使うこともできます
# df_mi[PanelData(df_mi).entity_ids == 0]
black exper hisp hours married educ union lwage expersq occupation
nr year
13 1980 0 1 0 2672 0 14 0 1.197540 1 9
1981 0 2 0 2320 0 14 1 1.853060 4 9
1982 0 3 0 2940 0 14 0 1.344462 9 9
1983 0 4 0 2960 0 14 0 1.433213 16 9
1984 0 5 0 3071 0 14 0 1.568125 25 5
1985 0 6 0 2864 0 14 0 1.699891 36 2
1986 0 7 0 2994 0 14 0 -0.720263 49 2
1987 0 8 0 2640 0 14 0 1.669188 64 2

クロスセクションデータ#

クロスセクションデータは、ある1時点のデータを複数の標本集めたものです。たとえば、2020年における47都道府県の人口データや、wage_panelデータセットにおけるyearが1980のみのデータがこれに当てはまります。

# wage_panelデータセットにおける1980年のクロスセクションデータ
df_mi.query("year == 1980")

# 以下でも同じ結果が得られます。
# df_mi.loc[(slice(None), 1980), :]
# df_mi[df_mi.index.get_level_values(1) == 1980]

# df_mi[PanelData(df_mi).time_ids == 0]

# df_mi.xs(1980, level='year')
black exper hisp hours married educ union lwage expersq occupation
nr year
13 1980 0 1 0 2672 0 14 0 1.197540 1 9
17 1980 0 4 0 2484 0 13 0 1.675962 16 2
18 1980 0 4 0 2332 1 12 0 1.515963 16 4
45 1980 0 2 0 1864 0 12 1 1.894115 4 7
110 1980 0 5 0 2080 0 12 1 1.948775 25 4
... ... ... ... ... ... ... ... ... ... ... ...
12451 1980 0 2 0 1584 0 14 0 1.066488 4 6
12477 1980 0 4 0 2080 0 12 1 2.213467 16 6
12500 1980 0 4 0 2008 1 12 0 0.972403 16 2
12534 1980 0 2 0 2080 0 11 0 1.840042 4 5
12548 1980 0 5 0 2000 0 9 0 1.130545 25 7

545 rows × 10 columns

繰り返しクロスセクションデータ#

繰り返しクロスセクションデータは、ユニットを”追跡できない”形で、複数時点観察したデータ構造です。パネルデータと異なる点としては、識別子に関する情報がないために、追跡できないことです。つまり、同一の観察個体に関して複数時点で観察していたとしても識別子が存在しなければ、パネルデータとして扱うことはできず、その利点を十分に活かすことはできません。したがって、繰り返しクロスセクションデータでは、固定効果モデルを使うことはできません。

また、繰り返しクロスセクションデータには、時点ごとにサンプルが異なっているようなデータも含まれます。たとえば、1年ごとにランダムサンプリングした人に調査を行うなどの場合がこれに当てはまります。複数の観察個体と時点で観測したデータとしては、パネルデータより繰り返しクロスセクションデータのほうが世の中に多いと思われます。たとえば、世論調査などがこれにあたります。

wage_panelのデータにおいて識別子であるnrがなかった場合のデータもこれに当たります。

# 繰り返しクロスセクションデータの例
df.drop(columns="nr")
year black exper hisp hours married educ union lwage expersq occupation
0 1980 0 1 0 2672 0 14 0 1.197540 1 9
1 1981 0 2 0 2320 0 14 1 1.853060 4 9
2 1982 0 3 0 2940 0 14 0 1.344462 9 9
3 1983 0 4 0 2960 0 14 0 1.433213 16 9
4 1984 0 5 0 3071 0 14 0 1.568125 25 5
... ... ... ... ... ... ... ... ... ... ... ...
4355 1983 0 8 0 2080 1 9 0 1.591879 64 5
4356 1984 0 9 0 2080 1 9 1 1.212543 81 5
4357 1985 0 10 0 2080 1 9 0 1.765962 100 5
4358 1986 0 11 0 2080 1 9 1 1.745894 121 5
4359 1987 0 12 0 3380 1 9 1 1.466543 144 5

4360 rows × 11 columns

wage_panelのデータにおいて識別子であるnrの列を落としたデータは、識別子に関する情報がないだけで、同一の観察個体を複数時点で観測したデータであるため、一見すると似たものに思われます。しかし、推定においては、ユニットを追跡できるかどうかが、ユニットの観察されていない要因をコントロールできるかに関わってきます。実際の推定値の比較は、パネルデータの利点と分析の例の章で行います。

複数ユニットの時系列データをパネルデータにする#

複数のロング形式の時系列データをパネルデータにするためには、識別子の付与を行った後に行方向に結合することが必要です。

実務上は、複数のユニットについてそれぞれ別にデータを取得していることが多いため、変数名が違っていたり、時間の抜けがあったり、時間の粒度が異なっていたりする可能性があることに注意が必要です。ただし、時間に抜けがある場合でも粒度が揃っていれば、不揃いなパネルデータとして分析ができます。

以下に時系列データの結合の例を説明します。

# 時系列データの準備(nr=13)
timeseries_nr_13 = df.query("nr == 13").drop(columns="nr").reset_index(drop=True)
timeseries_nr_13
year black exper hisp hours married educ union lwage expersq occupation
0 1980 0 1 0 2672 0 14 0 1.197540 1 9
1 1981 0 2 0 2320 0 14 1 1.853060 4 9
2 1982 0 3 0 2940 0 14 0 1.344462 9 9
3 1983 0 4 0 2960 0 14 0 1.433213 16 9
4 1984 0 5 0 3071 0 14 0 1.568125 25 5
5 1985 0 6 0 2864 0 14 0 1.699891 36 2
6 1986 0 7 0 2994 0 14 0 -0.720263 49 2
7 1987 0 8 0 2640 0 14 0 1.669188 64 2 
# 時系列データの準備(nr=17)
timeseries_nr_17 = df.query("nr == 17").drop(columns="nr").reset_index(drop=True)
timeseries_nr_17
year black exper hisp hours married educ union lwage expersq occupation
0 1980 0 4 0 2484 0 13 0 1.675962 16 2
1 1981 0 5 0 2804 0 13 0 1.518398 25 2
2 1982 0 6 0 2530 0 13 0 1.559191 36 2
3 1983 0 7 0 2340 0 13 0 1.725410 49 2
4 1984 0 8 0 2486 0 13 0 1.622022 64 2
5 1985 0 9 0 2164 0 13 0 1.608588 81 7
6 1986 0 10 0 2749 0 13 0 1.572385 100 7
7 1987 0 11 0 2476 0 13 0 1.820334 121 5 
# 識別子の付与
timeseries_nr_13["nr"] = 13
timeseries_nr_17["nr"] = 17

# 列の要素の確認
set(timeseries_nr_13.columns) == set(timeseries_nr_17.columns)

True

列の要素が同じかどうかは、たとえば set を使って確認できます。今回は列の要素が同じことが確認できたため、問題なく結合できます。

# timeseries_nr_13とtimeseries_nr_17を行方向に結合する
(
    pd.concat([timeseries_nr_13, timeseries_nr_17])
    .reset_index(drop=True)
    .set_index(["nr", "year"])
)
black exper hisp hours married educ union lwage expersq occupation
nr year
13 1980 0 1 0 2672 0 14 0 1.197540 1 9
1981 0 2 0 2320 0 14 1 1.853060 4 9
1982 0 3 0 2940 0 14 0 1.344462 9 9
1983 0 4 0 2960 0 14 0 1.433213 16 9
1984 0 5 0 3071 0 14 0 1.568125 25 5
1985 0 6 0 2864 0 14 0 1.699891 36 2
1986 0 7 0 2994 0 14 0 -0.720263 49 2
1987 0 8 0 2640 0 14 0 1.669188 64 2
17 1980 0 4 0 2484 0 13 0 1.675962 16 2
1981 0 5 0 2804 0 13 0 1.518398 25 2
1982 0 6 0 2530 0 13 0 1.559191 36 2
1983 0 7 0 2340 0 13 0 1.725410 49 2
1984 0 8 0 2486 0 13 0 1.622022 64 2
1985 0 9 0 2164 0 13 0 1.608588 81 7
1986 0 10 0 2749 0 13 0 1.572385 100 7
1987 0 11 0 2476 0 13 0 1.820334 121 5

複数期間のクロスセクションデータをパネルデータにする#

複数のロング形式のクロスセクションデータをパネルデータにするためには、時点に関する情報を変数に含めたうえで、行方向に結合することが必要です。

データをいつ取得したかという情報は残りやすいことや、データを取得する主体が同じことが多いことから、データ構造の変更などが少なく、比較的実施しやすいと考えられます。

以下にクロスセクションデータの結合の例を説明します。

# クロスセクションデータの準備(1980年)
cross_sectional_1980 = (
    df.query("year == 1980").drop(columns="year").reset_index(drop=True)
)
cross_sectional_1980
nr black exper hisp hours married educ union lwage expersq occupation
0 13 0 1 0 2672 0 14 0 1.197540 1 9
1 17 0 4 0 2484 0 13 0 1.675962 16 2
2 18 0 4 0 2332 1 12 0 1.515963 16 4
3 45 0 2 0 1864 0 12 1 1.894115 4 7
4 110 0 5 0 2080 0 12 1 1.948775 25 4
... ... ... ... ... ... ... ... ... ... ... ...
540 12451 0 2 0 1584 0 14 0 1.066488 4 6
541 12477 0 4 0 2080 0 12 1 2.213467 16 6
542 12500 0 4 0 2008 1 12 0 0.972403 16 2
543 12534 0 2 0 2080 0 11 0 1.840042 4 5
544 12548 0 5 0 2000 0 9 0 1.130545 25 7

545 rows × 11 columns

# クロスセクションデータの準備(1981年)
cross_sectional_1981 = (
    df.query("year == 1981").drop(columns="year").reset_index(drop=True)
)
cross_sectional_1981
nr black exper hisp hours married educ union lwage expersq occupation
0 13 0 2 0 2320 0 14 1 1.853060 4 9
1 17 0 5 0 2804 0 13 0 1.518398 25 2
2 18 0 5 0 2116 1 12 0 1.735379 25 4
3 45 0 3 0 2021 0 12 1 1.471159 9 6
4 110 0 6 0 2080 0 12 0 1.962259 36 4
... ... ... ... ... ... ... ... ... ... ... ...
540 12451 0 3 0 1268 0 14 0 1.937311 9 1
541 12477 0 5 0 2080 0 12 1 2.222542 25 5
542 12500 0 5 0 3190 0 12 0 1.324886 25 9
543 12534 0 3 0 2000 0 11 0 2.174752 9 5
544 12548 0 6 0 2112 0 9 0 1.311603 36 5

545 rows × 11 columns

# 時点に関する情報を追加
cross_sectional_1980["year"] = 1980
cross_sectional_1981["year"] = 1981

# cross_sectional_1980とcross_sectional_1981を行方向に結合する
(
    pd.concat([cross_sectional_1980, cross_sectional_1981])
    .reset_index(drop=True)
    .set_index(["nr", "year"])
)
black exper hisp hours married educ union lwage expersq occupation
nr year
13 1980 0 1 0 2672 0 14 0 1.197540 1 9
17 1980 0 4 0 2484 0 13 0 1.675962 16 2
18 1980 0 4 0 2332 1 12 0 1.515963 16 4
45 1980 0 2 0 1864 0 12 1 1.894115 4 7
110 1980 0 5 0 2080 0 12 1 1.948775 25 4
... ... ... ... ... ... ... ... ... ... ... ...
12451 1981 0 3 0 1268 0 14 0 1.937311 9 1
12477 1981 0 5 0 2080 0 12 1 2.222542 25 5
12500 1981 0 5 0 3190 0 12 0 1.324886 25 9
12534 1981 0 3 0 2000 0 11 0 2.174752 9 5
12548 1981 0 6 0 2112 0 9 0 1.311603 36 5

1090 rows × 10 columns

繰り返しクロスセクションデータをパネルデータにする#

繰り返しクロスセクションデータは、各観測データがどのユニットであるかを特定し、識別子を振ることでパネルデータにすることができます。ただし、これは事後的に行うことは難しい場合が多いため、データ取得段階から設計することが望ましいです。

繰り返しクロスセクションデータを事後的にパネルデータを作成する場合には、なんらかのドメイン知識を用いて観測値ごとにユニットを特定し識別子を付与する必要があります。したがってここでは繰り返しクロスセクションデータをパネルデータにする方法の説明は行わず、次に説明する擬似的にパネルデータとして扱う方法を主に説明します。

繰り返しクロスセクションデータを擬似的にパネルデータとして扱う#

識別子の付与が現実的でない場合、時間不変な共通の特徴を持つコホート(英:cohort)ごとに、平均を取ることで、疑似パネルデータを作り、分析することができます。たとえば、年齢がわかっている場合、各観測データを1990年生まれ、1991年生まれ...と分け、世代ごとの平均を取ることで、疑似的なパネルデータとみなして分析ができます。この場合、年代ごとに固有の特徴がコントロールされたと解釈できます。

以下では、wage_panelで、exper(経験年数)をもとに、就業開始年をコホートとみなした疑似パネルデータを作成する処理の例を説明します。ただし、実際には個人によって就業開始年が異なる可能性や一時的に労働市場を離脱している期間がある可能性があることから、コホートとして不適です。そのため、あくまでも例としてどのような処理を行うかに焦点を当てて説明します。

# 繰り返しクロスセクションデータの準備
df_repeated_cs = df.drop(columns="nr")
df_repeated_cs
year black exper hisp hours married educ union lwage expersq occupation
0 1980 0 1 0 2672 0 14 0 1.197540 1 9
1 1981 0 2 0 2320 0 14 1 1.853060 4 9
2 1982 0 3 0 2940 0 14 0 1.344462 9 9
3 1983 0 4 0 2960 0 14 0 1.433213 16 9
4 1984 0 5 0 3071 0 14 0 1.568125 25 5
... ... ... ... ... ... ... ... ... ... ... ...
4355 1983 0 8 0 2080 1 9 0 1.591879 64 5
4356 1984 0 9 0 2080 1 9 1 1.212543 81 5
4357 1985 0 10 0 2080 1 9 0 1.765962 100 5
4358 1986 0 11 0 2080 1 9 1 1.745894 121 5
4359 1987 0 12 0 3380 1 9 1 1.466543 144 5

4360 rows × 11 columns

# 就業開始年をcohortとして追加
df_repeated_cs["cohort"] = df_repeated_cs["year"] - df_repeated_cs["exper"]

# 疑似パネルデータの作成
pseudo_panel = (
    df_repeated_cs.drop(columns="occupation").groupby(["year", "cohort"]).mean()
)
pseudo_panel.head(24)
black exper hisp hours married educ union lwage expersq
year cohort
1980 1969 0.000000 11.0 1.000000 2130.000000 0.000000 4.500000 0.500000 1.400766 121.0
1970 0.000000 10.0 1.000000 2496.000000 1.000000 6.000000 0.000000 1.265678 100.0
1971 0.142857 9.0 0.285714 2161.857143 0.571429 7.142857 0.142857 1.459132 81.0
1972 0.000000 8.0 0.500000 2219.000000 0.250000 7.750000 0.250000 1.301495 64.0
1973 0.250000 7.0 0.125000 2163.875000 0.250000 8.375000 0.125000 1.212670 49.0
1974 0.166667 6.0 0.166667 2050.750000 0.416667 9.000000 0.416667 1.284774 36.0
1975 0.212766 5.0 0.085106 2108.957447 0.319149 11.382979 0.361702 1.573773 25.0
1976 0.136364 4.0 0.238636 2033.750000 0.238636 11.681818 0.352273 1.430326 16.0
1977 0.111111 3.0 0.157407 2118.361111 0.194444 11.712963 0.240741 1.468764 9.0
1978 0.090047 2.0 0.109005 1856.725118 0.127962 12.222749 0.208531 1.366195 4.0
1979 0.090909 1.0 0.163636 1583.709091 0.054545 12.854545 0.181818 1.179810 1.0
1980 0.000000 0.0 0.500000 2114.000000 0.500000 14.000000 0.000000 1.610015 0.0
1981 1969 0.000000 12.0 1.000000 2101.000000 0.000000 4.500000 0.000000 1.487130 144.0
1970 0.000000 11.0 1.000000 2168.000000 1.000000 6.000000 0.000000 1.711102 121.0
1971 0.142857 10.0 0.285714 2232.428571 0.857143 7.142857 0.000000 1.392692 100.0
1972 0.000000 9.0 0.500000 2159.750000 0.500000 7.750000 0.000000 1.584002 81.0
1973 0.250000 8.0 0.125000 2446.625000 0.375000 8.375000 0.250000 1.201998 64.0
1974 0.166667 7.0 0.166667 2356.500000 0.500000 9.000000 0.250000 1.197461 49.0
1975 0.212766 6.0 0.085106 2223.893617 0.404255 11.382979 0.425532 1.572072 36.0
1976 0.136364 5.0 0.238636 2163.647727 0.329545 11.681818 0.318182 1.564589 25.0
1977 0.111111 4.0 0.157407 2074.879630 0.305556 11.712963 0.268519 1.579509 16.0
1978 0.090047 3.0 0.109005 1973.369668 0.232227 12.222749 0.213270 1.497159 9.0
1979 0.090909 2.0 0.163636 1892.381818 0.145455 12.854545 0.163636 1.425094 4.0
1980 0.000000 1.0 0.500000 2402.500000 0.500000 14.000000 0.000000 1.658966 1.0

パネルデータの利点と分析の例#

パネルデータの利点と分析方法について説明します。

パネルデータの利点の1つとして、固定効果モデルを利用した回帰分析があります。固定効果とは、観察できないが時間を通じて一定の変数を表します。たとえば、個人の生まれつきの能力や特性、その地域特有の文化といった要素を固定効果として表現することがあります。

固定効果モデルを使用することで、追加的な変数を考えることなく、欠落変数バイアスの一部に対処できます。具体的には、パネルデータの特性を活かして、ユニットに特有の、時間を通じて一定であるような、観察されていない変数によって生じる欠落変数バイアスの影響をコントロールできます。たとえば、個人の生まれつきの能力や特性、その地域特有の文化といった要素の影響をコントロールできます。分析の際に必要な要素がすべて手元のデータセットに含まれているとは限りませんし、能力や特性、文化のような要素は定量化しづらいと考えられます。しかし、これらの要素が時間を通じて変わらないと仮定できるのあれば、固定効果モデルによってコントロールできます。たとえば、その地域特有の文化は、時間を通じて変わらない要素と考えられるため、実際に観察・定量化できていなくても、パネルデータを使うことで、地域固定効果としてモデルに含め、コントロールできます。

この利点のために、社会科学ではパネルデータが広く利用されています。ただし、パネルデータを使った固定効果モデルは、観察された変数のうち時間を通じて変わらないものの効果を知ることはできないため、その点に関しては注意が必要です。

この章では、linearmodels を使い、パネルデータにおける記述統計の確認と固定効果モデルによる重回帰分析を行います。データセットは引き続き wage_panel を使います。

可視化#

まずは単純に労働組合の加入と賃金をプロットします。ここで賃金の値は対数値であることに注意してください。

# ヒストグラムの比較
import matplotlib.pyplot as plt

plt.hist(
    df.query("union == 1")["lwage"], bins=20, alpha=0.5, label="組合員", density=True
)
# 平均の線を追加
plt.axvline(
    df.query("union == 1")["lwage"].mean(),
    color="blue",
    linestyle="dashed",
    linewidth=1,
)

plt.hist(
    df.query("union == 0")["lwage"], bins=20, alpha=0.5, label="非組合員", density=True
)
# 平均の線を追加
plt.axvline(
    df.query("union == 0")["lwage"].mean(),
    color="orange",
    linestyle="dashed",
    linewidth=1,
)

plt.xlabel("Wages")
plt.ylabel("Frequency")
plt.title("Wages by Union Membership")
plt.legend()
plt.show()
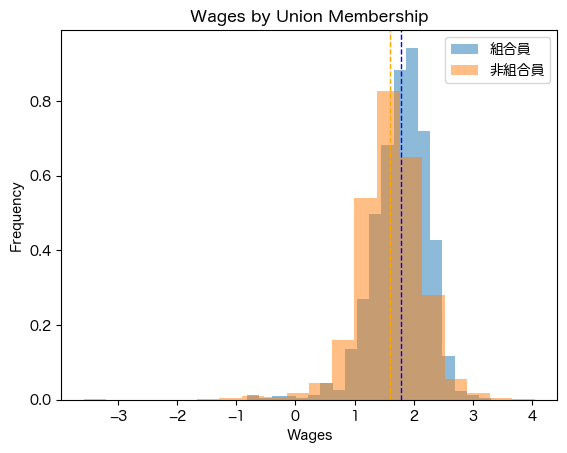
../_images/1ea2a622b2a7dbf25ab6aeffa28b62ff3e49fc54229c599ad1290453495cd178.png

点線がそれぞれの集団の平均です。労働組合に入っているほうがわずかに賃金が高く見えます。

しかし、これは観察されない生まれつきのその人固有の能力のような異質性に影響を受けている可能性があります。したがって、ある個人を追跡して、その個人内の変動に着目することで、労働組合への参加が賃金に与える影響を考えることができます。

次に、個人ごとの時系列を描画してみます。

import matplotlib.pyplot as plt
import random

# ユニークなnrを取得
unique_nr = df["nr"].unique()

y_min, y_max = 0, 3

# ランダムに10人の個人の賃金をプロット
random.seed(430 * 29)
unique_nr = random.sample(list(unique_nr), 10)

ncols = 2
nrows = len(unique_nr) // ncols

fig, axes = plt.subplots(nrows=nrows, ncols=ncols, figsize=(10, nrows * 3))
axes = axes.flatten()

for i, nr_num in enumerate(unique_nr):
    ax = axes[i]
    df_nr = df.query("nr == @nr_num").reset_index(drop=True)
    colors = ["red" if union == 1 else "gray" for union in df_nr["union"]]
    # 線を描画
    ax.plot(
        df_nr.year,
        df_nr["lwage"],
        marker="o",
        label=f"nr {nr_num}",
        color="gray",
        alpha=0.5,
        markersize=5,
        linewidth=1,
    )
    # 個々の点に色を付ける
    for j, color in enumerate(colors):
        ax.plot(
            df_nr.year[j], df_nr["lwage"].iloc[j], marker="o", color=color, markersize=7
        )
    ax.set_ylim(y_min, y_max)
    ax.legend()
    ax.set_xlabel("Year")
    ax.set_ylabel("Log Wage")

# 不足しているサブプロットを非表示にする
for k in range(i + 1, len(axes)):
    fig.delaxes(axes[k])

plt.tight_layout()
plt.show()
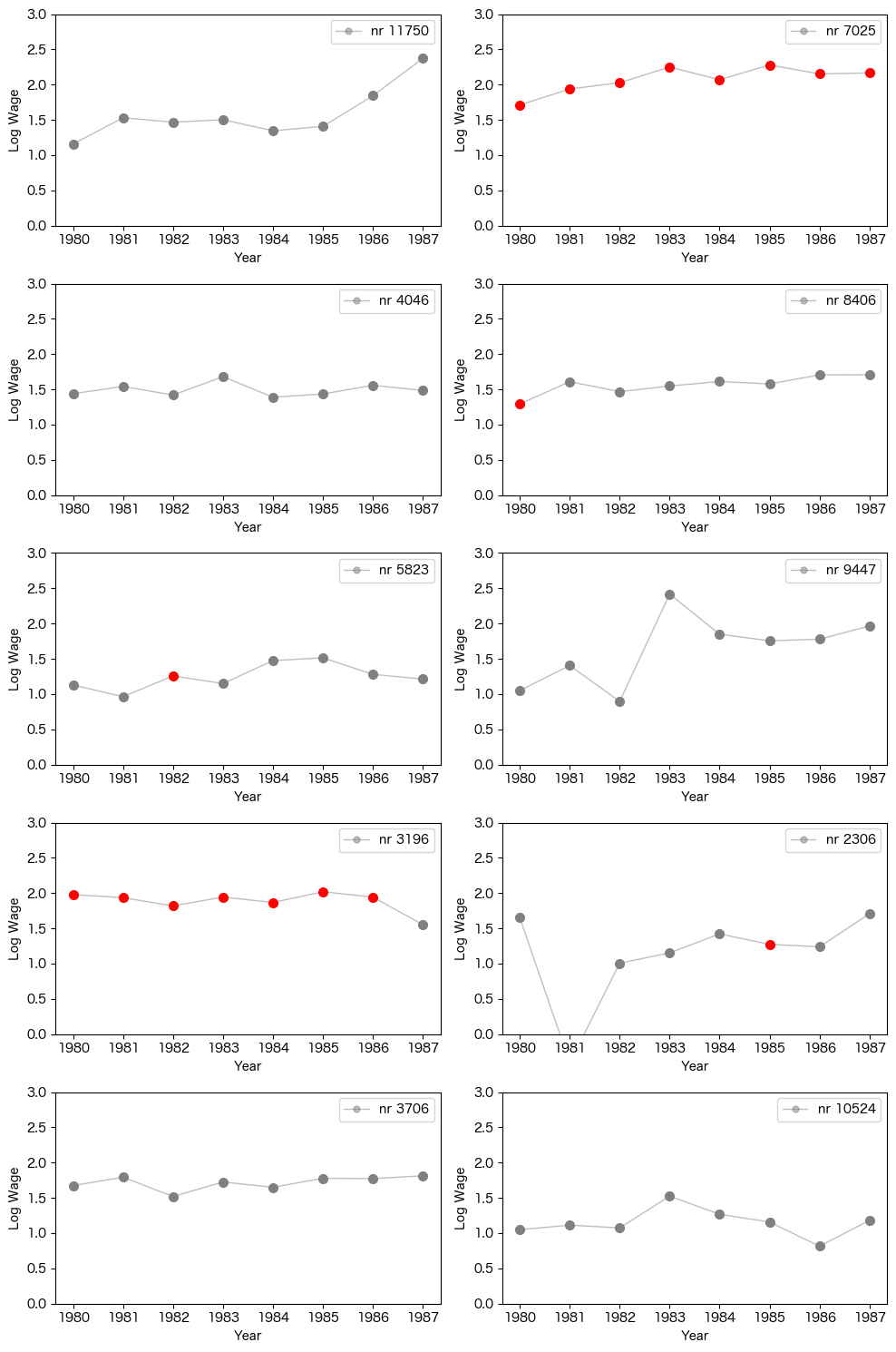
../_images/7a8e79de8134657da6571a1b665826da06246006bd4f7eb5ec2c3bf9a5764bb3.png

赤丸が労働組合に入っている年を表します。個人の変動に着目すると、労働組合に入っている時期の賃金が特別高いようには見えません。

記述統計#

ここでは、linearmodels の PanelData オブジェクトを使って、それぞれの個体に関する記述統計と各年における記述統計を見てみます。

from linearmodels.panel.data import PanelData

PanelData(df_mi).mean()
black exper hisp hours married educ union lwage expersq occupation
nr
13 0.0 4.5 0.0 2807.625 0.000 14.0 0.125 1.255652 25.5 5.875
17 0.0 7.5 0.0 2504.125 0.000 13.0 0.000 1.637786 61.5 3.625
18 0.0 7.5 0.0 2350.500 1.000 12.0 0.000 2.034387 61.5 3.125
45 0.0 5.5 0.0 2225.875 0.125 12.0 0.250 1.773664 35.5 5.625
110 0.0 8.5 0.0 2108.000 0.500 12.0 0.125 2.055129 77.5 2.750
... ... ... ... ... ... ... ... ... ... ...
12451 0.0 5.5 0.0 1700.750 0.625 14.0 0.000 1.654297 35.5 2.375
12477 0.0 7.5 0.0 2040.000 0.750 12.0 1.000 2.178360 61.5 6.000
12500 0.0 7.5 0.0 2635.500 0.750 12.0 0.000 1.315911 61.5 5.625
12534 0.0 5.5 0.0 2035.000 0.750 11.0 0.000 2.171136 35.5 5.250
12548 0.0 8.5 0.0 2236.500 0.625 9.0 0.375 1.382181 77.5 5.250

545 rows × 10 columns

引数に年を指定することもできます。

PanelData(df_mi).mean("year")
black exper hisp hours married educ union lwage expersq occupation
year
1980 0.115596 3.014679 0.155963 1949.834862 0.185321 11.766972 0.251376 1.393477 11.822018 5.546789
1981 0.115596 4.014679 0.155963 2060.119266 0.288073 11.766972 0.249541 1.512867 18.851376 5.321101
1982 0.115596 5.014679 0.155963 2106.313761 0.357798 11.766972 0.256881 1.571667 27.880734 5.067890
1983 0.115596 6.014679 0.155963 2207.884404 0.447706 11.766972 0.245872 1.619263 38.910092 4.992661
1984 0.115596 7.014679 0.155963 2260.708257 0.500917 11.766972 0.251376 1.690295 51.939450 4.794495
1985 0.115596 8.014679 0.155963 2280.170642 0.541284 11.766972 0.223853 1.739410 66.968807 4.849541
1986 0.115596 9.014679 0.155963 2310.302752 0.576147 11.766972 0.211009 1.799719 83.998165 4.739450
1987 0.115596 10.014679 0.155963 2354.724771 0.614679 11.766972 0.262385 1.866479 103.027523 4.596330

労働組合への参加率の推移などを確認できます。

固定効果モデル#

固定効果モデル(英: fixed effect regression model)とは、データがパネルデータの構造を持つとき、重回帰分析のモデルに、ユニットごとに異なる定数項を加えたモデルです。これによって、主体に特有で、時間を通じて不変であるような、観察されていない変数の影響をコントロールできます。後述しますが、固定効果モデルでは時間を通じて変わらない変数を含めることはできません。

paneldata_long

以上のような、\(Y_{it}, X1_{it}, ... ,Xk_{it}\) というパネルデータを例に考えます。このとき、固定効果モデルは、以下のように表せます。

\[ Y_{it} = \alpha_i + \beta_1 X1_{it} + \beta_2 X2_{it} + \dots + \beta_k Xk_{it} + u_{it} \]

重回帰分析のモデルに\(\alpha_i\)の項を加えることで、観察個体\(i\)ごとに異なるが、時間\(t\)に依存しない要素をモデルに含めています。この\(\alpha_i\)は、観察されていない要素についてもまとめて表現されているため、欠落変数によるバイアスを回避できます。これはたとえば、個人の生まれつきの能力や地域特有の文化のような変数として観察することが難しい要素も、固定効果モデルであれば、時間を通じて一定であるという仮定のもとコントロールできることを示しています。

ユニット間に共通の時間的な変動を固定効果として含めることもできます。これを時間固定効果と呼びます。たとえば、サンプルに含まれるユニット全員が影響を受けるような大規模な制度変更や、景気などの影響をコントロールできます。\(\lambda_t\) が時間固定効果を表します。

\[ Y_{it} = \lambda_t + \beta_1 X1_{it} + \beta_2 X2_{it} + \dots + \beta_k Xk_{it} + u_{it} \]

ユニットと時間、両方の固定効果を含めることもでき、このときモデルは以下のように表されます。\(\alpha_i\) がユニット固定効果を表し、 \(\lambda_t\) が時間固定効果を表します。

\[ Y_{it} = \alpha_i + \lambda_t + \beta_1 X1_{it} + \beta_2 X2_{it} + \dots + \beta_k Xk_{it} + u_{it} \]

具体例として、引き続き、労働組合と賃金を例に固定効果による推定を行います。ここでは、パネルデータの構造を明示的に考慮することなく、通常のOLSと同じように分析する方法であるPooled OLSによる分析結果と比較を行います。時間を通じて変わる変数として、unionとmarriage[2]、expersqを説明変数に加えた固定効果モデルと、同様の変数を加えたPooled OLSに加えて、時間を通じて変わらない変数を追加したPooled OLSの結果を比較します。

wage_panelを利用した分析では、たとえば以下のようなモデルを推定します。ここで興味があるパラメータは労働組合の加入状況を表すunionにかかる係数 \(\delta\) です。

\[ \text{log(wage)}_{it} = \alpha_i + \delta \ \text{union}_{it} + \beta_1 \ \text{marriage}_{it} + \beta_2 \ \text{expersq}_{it} + u_{it} \]

一方で、同様の変数を用いた場合、Pooled OLSでは、以下の式を推定します。

\[ \text{log(wage)}_{it} = \alpha + \delta \ \text{union}_{it} + \beta_1 \ \text{marriage}_{it} + \beta_2 \ \text{expersq}_{it} + u_{it} \]

数式上の違いは \(\alpha\) に添字 \(i\) があるかどうか、すなわち、ユニットごとに異なる定数 \(\alpha\) の値(=固定効果)を推定しているかどうかです。

実際に linearmodels を使って推定した結果を比較します。 linearmodels は、stasmodelsと同じように推定できます。 entity_effects = True[3] とすることで、ユニットレベルの固定効果を含めて推定できます。 time_effects = Trueとすることで、時間固定効果を含めることができます。

# 固定効果モデルによる重回帰分析
exog_vars = ["union", "married", "expersq"]
exog = df_mi[exog_vars]
mod = linearmodels.PanelOLS(df_mi.lwage, exog, entity_effects=True, time_effects=False)
fe_result = mod.fit(cov_type="clustered", cluster_entity=True)
print(fe_result)

                          PanelOLS Estimation Summary                           
================================================================================
Dep. Variable:                  lwage   R-squared:                        0.1365
Estimator:                   PanelOLS   R-squared (Between):              0.2655
No. Observations:                4360   R-squared (Within):               0.1365
Date:                Thu, Mar 06 2025   R-squared (Overall):              0.2599
Time:                        20:32:35   Log-likelihood                   -1439.0
Cov. Estimator:             Clustered                                           
                                        F-statistic:                      200.87
Entities:                         545   P-value                           0.0000
Avg Obs:                       8.0000   Distribution:                  F(3,3812)
Min Obs:                       8.0000                                           
Max Obs:                       8.0000   F-statistic (robust):             114.81
                                        P-value                           0.0000
Time periods:                       8   Distribution:                  F(3,3812)
Avg Obs:                       545.00                                           
Min Obs:                       545.00                                           
Max Obs:                       545.00                                           
                                                                                
                             Parameter Estimates                              
==============================================================================
            Parameter  Std. Err.     T-stat    P-value    Lower CI    Upper CI
------------------------------------------------------------------------------
union          0.0828     0.0238     3.4818     0.0005      0.0362      0.1294
married        0.1073     0.0218     4.9256     0.0000      0.0646      0.1501
expersq        0.0037     0.0002     15.646     0.0000      0.0032      0.0042
==============================================================================

F-test for Poolability: 9.3360
P-value: 0.0000
Distribution: F(544,3812)

Included effects: Entity

# ユニット固定効果と時間固定効果を含むモデル
exog_vars = ["union", "married", "expersq"]
exog = df_mi[exog_vars]
mod = linearmodels.PanelOLS(df_mi.lwage, exog, entity_effects=True, time_effects=True)
fe_time_result = mod.fit(cov_type="clustered", cluster_entity=True, cluster_time=True)
print(fe_time_result)

                          PanelOLS Estimation Summary                           
================================================================================
Dep. Variable:                  lwage   R-squared:                        0.0216
Estimator:                   PanelOLS   R-squared (Between):             -0.2717
No. Observations:                4360   R-squared (Within):              -0.4809
Date:                Thu, Mar 06 2025   R-squared (Overall):             -0.2808
Time:                        20:32:35   Log-likelihood                   -1324.8
Cov. Estimator:             Clustered                                           
                                        F-statistic:                      27.959
Entities:                         545   P-value                           0.0000
Avg Obs:                       8.0000   Distribution:                  F(3,3805)
Min Obs:                       8.0000                                           
Max Obs:                       8.0000   F-statistic (robust):             23.126
                                        P-value                           0.0000
Time periods:                       8   Distribution:                  F(3,3805)
Avg Obs:                       545.00                                           
Min Obs:                       545.00                                           
Max Obs:                       545.00                                           
                                                                                
                             Parameter Estimates                              
==============================================================================
            Parameter  Std. Err.     T-stat    P-value    Lower CI    Upper CI
------------------------------------------------------------------------------
union          0.0800     0.0234     3.4242     0.0006      0.0342      0.1258
married        0.0467     0.0165     2.8312     0.0047      0.0144      0.0790
expersq       -0.0052     0.0008    -6.6189     0.0000     -0.0067     -0.0036
==============================================================================

F-test for Poolability: 10.067
P-value: 0.0000
Distribution: F(551,3805)

Included effects: Entity, Time

import statsmodels.api as sm
from linearmodels.panel import PooledOLS

# 通常の重回帰分析(Pooled OLS)、時定変数なし
exog_vars = ["expersq", "married", "union"]
exog = sm.add_constant(df_mi[exog_vars])
mod = PooledOLS(df_mi.lwage, exog)
pooled_result = mod.fit(cov_type="clustered", cluster_entity=True)
print(pooled_result)

                          PooledOLS Estimation Summary                          
================================================================================
Dep. Variable:                  lwage   R-squared:                        0.0683
Estimator:                  PooledOLS   R-squared (Between):              0.0489
No. Observations:                4360   R-squared (Within):               0.0908
Date:                Thu, Mar 06 2025   R-squared (Overall):              0.0683
Time:                        20:32:35   Log-likelihood                   -3285.2
Cov. Estimator:             Clustered                                           
                                        F-statistic:                      106.43
Entities:                         545   P-value                           0.0000
Avg Obs:                       8.0000   Distribution:                  F(3,4356)
Min Obs:                       8.0000                                           
Max Obs:                       8.0000   F-statistic (robust):             40.265
                                        P-value                           0.0000
Time periods:                       8   Distribution:                  F(3,4356)
Avg Obs:                       545.00                                           
Min Obs:                       545.00                                           
Max Obs:                       545.00                                           
                                                                                
                             Parameter Estimates                              
==============================================================================
            Parameter  Std. Err.     T-stat    P-value    Lower CI    Upper CI
------------------------------------------------------------------------------
const          1.4648     0.0252     58.027     0.0000      1.4153      1.5143
expersq        0.0012     0.0003     4.1210     0.0000      0.0006      0.0017
married        0.1900     0.0272     6.9754     0.0000      0.1366      0.2434
union          0.1704     0.0298     5.7273     0.0000      0.1121      0.2287
==============================================================================

import statsmodels.api as sm
from linearmodels.panel import PooledOLS

# 通常の重回帰分析(Pooled OLS)、時定変数あり
exog_vars = ["black", "hisp", "exper", "expersq", "married", "educ", "union"]
exog = sm.add_constant(df_mi[exog_vars])
mod = PooledOLS(df_mi.lwage, exog)
pooled_time_invariant_result = mod.fit(cov_type="clustered", cluster_entity=True)
print(pooled_time_invariant_result)

                          PooledOLS Estimation Summary                          
================================================================================
Dep. Variable:                  lwage   R-squared:                        0.1866
Estimator:                  PooledOLS   R-squared (Between):              0.2027
No. Observations:                4360   R-squared (Within):               0.1679
Date:                Thu, Mar 06 2025   R-squared (Overall):              0.1866
Time:                        20:32:35   Log-likelihood                   -2989.2
Cov. Estimator:             Clustered                                           
                                        F-statistic:                      142.61
Entities:                         545   P-value                           0.0000
Avg Obs:                       8.0000   Distribution:                  F(7,4352)
Min Obs:                       8.0000                                           
Max Obs:                       8.0000   F-statistic (robust):             59.188
                                        P-value                           0.0000
Time periods:                       8   Distribution:                  F(7,4352)
Avg Obs:                       545.00                                           
Min Obs:                       545.00                                           
Max Obs:                       545.00                                           
                                                                                
                             Parameter Estimates                              
==============================================================================
            Parameter  Std. Err.     T-stat    P-value    Lower CI    Upper CI
------------------------------------------------------------------------------
const         -0.0347     0.1200    -0.2892     0.7724     -0.2700      0.2006
black         -0.1438     0.0501    -2.8727     0.0041     -0.2420     -0.0457
hisp           0.0157     0.0392     0.4008     0.6886     -0.0611      0.0925
exper          0.0892     0.0124     7.1728     0.0000      0.0648      0.1136
expersq       -0.0028     0.0009    -3.2747     0.0011     -0.0046     -0.0011
married        0.1077     0.0261     4.1314     0.0000      0.0566      0.1588
educ           0.0994     0.0092     10.802     0.0000      0.0813      0.1174
union          0.1801     0.0276     6.5343     0.0000      0.1260      0.2341
==============================================================================

# 比較
print(
    linearmodels.panel.results.compare(
        {
            "Entity Fixed Effects": fe_result,
            "Entity+Time Fixed Effects": fe_time_result,
            "Pooled OLS": pooled_result,
            "Pooled OLS + Controls": pooled_time_invariant_result,
        },
        precision="std_errors",
        stars=True,
    )
)

                                             Model Comparison                                             
==========================================================================================================
                        Entity Fixed Effects Entity+Time Fixed Effects    Pooled OLS Pooled OLS + Controls
----------------------------------------------------------------------------------------------------------
Dep. Variable                          lwage                     lwage         lwage                 lwage
Estimator                           PanelOLS                  PanelOLS     PooledOLS             PooledOLS
No. Observations                        4360                      4360          4360                  4360
Cov. Est.                          Clustered                 Clustered     Clustered             Clustered
R-squared                             0.1365                    0.0216        0.0683                0.1866
R-Squared (Within)                    0.1365                   -0.4809        0.0908                0.1679
R-Squared (Between)                   0.2655                   -0.2717        0.0489                0.2027
R-Squared (Overall)                   0.2599                   -0.2808        0.0683                0.1866
F-statistic                           200.87                    27.959        106.43                142.61
P-value (F-stat)                      0.0000                    0.0000        0.0000                0.0000
=====================            ===========              ============   ===========          ============
union                              0.0828***                 0.0800***     0.1704***             0.1801***
                                    (0.0238)                  (0.0234)      (0.0298)              (0.0276)
married                            0.1073***                 0.0467***     0.1900***             0.1077***
                                    (0.0218)                  (0.0165)      (0.0272)              (0.0261)
expersq                            0.0037***                -0.0052***     0.0012***            -0.0028***
                                    (0.0002)                  (0.0008)      (0.0003)              (0.0009)
const                                                                      1.4648***               -0.0347
                                                                            (0.0252)              (0.1200)
black                                                                                           -0.1438***
                                                                                                  (0.0501)
hisp                                                                                                0.0157
                                                                                                  (0.0392)
exper                                                                                            0.0892***
                                                                                                  (0.0124)
educ                                                                                             0.0994***
                                                                                                  (0.0092)
=======================        =============            ============== =============        ==============
Effects                               Entity                    Entity                                    
                                                                  Time                                    
----------------------------------------------------------------------------------------------------------

Std. Errors reported in parentheses
\[\begin{split} \begin{aligned} \textbf{Entity FE:} \quad \widehat{\log(\text{wage})}_{it} &= \alpha_i + 0.0828\,\text{union}_{it} + 0.1073\,\text{married}_{it} + 0.0037\,\text{expersq}_{it}\ , \\[1ex] \textbf{Entity + Time FE:} \quad \widehat{\log(\text{wage})}_{it} &= \alpha_i + \gamma_t + 0.0800\,\text{union}_{it} + 0.0467\,\text{married}_{it} - 0.0052\,\text{expersq}_{it}\ , \\[1ex] \textbf{Pooled OLS:} \quad \widehat{\log(\text{wage})}_{it} &= 1.4648 + 0.1704\,\text{union}_{it} + 0.1900\,\text{married}_{it} + 0.0012\,\text{expersq}_{it}\ , \\[1ex] \textbf{Pooled OLS + Controls:} \quad \widehat{\log(\text{wage})}_{it} &= -0.0347 + 0.1801\,\text{union}_{it} + 0.1077\,\text{married}_{it} - 0.0028\,\text{expersq}_{it} \\ &\quad\quad - 0.1438\,\text{black}_{it} + 0.0157\,\text{hisp}_{it} + 0.0892\,\text{exper}_{it} + 0.0994\,\text{educ}_{it}\ . \end{aligned} \end{split}\]

unionに対する係数の値、すなわち、労働組合に入ることによる賃金に対する効果が、固定効果モデルでは約8%、通常のOLSでは約17-18%と推定されました。10%ポイント近くの差は、すべてが必ずしも欠落変数バイアスの影響と言い切れるわけではないですが、人種や教育年数以外の観察されていない個人に固有で時間不変の要素がコントロールされた結果と考えられます。

以上の分析では linearmodels のライブラリを使用して分析していますが、固定効果モデルを推定する場合には方法がいくつかあり、そのうち最も実装が簡単でイメージがしやすいと思われるものは、ユニット \(i\) ごとのダミー変数を入れて、OLSを行う方法です。この方法は、パネルデータが不揃いな場合でも特別な処理を必要とすることなく同じように分析することができるという特徴があります。

推定結果が一致することを以下で確認してみます。

import statsmodels.api as sm
from linearmodels.panel import PooledOLS

# nrをダミー変数化
unit = pd.Categorical(df.nr)
df_dummy = df.set_index(["nr", "year"])
df_dummy["unit"] = unit

# df_dummy.head()

# 通常の重回帰分析(Pooled OLS)
exog_vars = ["expersq", "married", "union", "unit"]
exog = sm.add_constant(df_dummy[exog_vars])
mod = PooledOLS(df_dummy.lwage, exog)
dummy_result = mod.fit(cov_type="clustered", cluster_entity=True)
# 出力が長いので係数のみ表示
print(
    (
        linearmodels.panel.results.compare(
            {"Fixed Effects": fe_result, "Dummy Variable": dummy_result},
            stars=True,
            precision="std_errors",
        )
    ).params
)

            Fixed Effects  Dummy Variable
union            0.082762        0.082762
married          0.107343        0.107343
expersq          0.003699        0.003699
const                 NaN        1.150980
unit.17               NaN        0.259312
...                   ...             ...
unit.12451            NaN        0.304910
unit.12477            NaN        0.636617
unit.12500            NaN       -0.143071
unit.12534            NaN        0.808331
unit.12548            NaN       -0.153603

[548 rows x 2 columns]

union, married, expersq にかかる係数が一致していることが確認できます。

固定効果モデルの限界#

固定効果モデルは、時間を通じて一定な変数の効果を知ることができないという限界があります。たとえば、人種や教育年数などの時間を通じて変化しない(しづらい)変数はモデルに含められないということです。その理由としては、時間を通じて変化しない変数をモデルに含めると、固定効果と完全な多重共線性が発生してしまうためです。これは先述した固定効果がダミー変数を入れることで推定できることをイメージしてもらえばわかりやすいかもしれません。

ここでは取り上げませんが、上記の課題を解決する方法として、変量効果モデルなどのパネルデータを使った他のモデルや操作変数法といった手法が存在します。

小括#

本稿では、パネルデータの形式と作成方法、そして固定効果モデルによる分析の例を解説しました。 パネルデータの作成は簡単なことではないですが、パネルデータには、固定効果モデルの利用によって、時間を通じて変わらない要素をコントロールできるという強力な利点があるため、社会科学の分析でよく使われているデータ構造です。

また、固定効果モデルを発展させた手法として、差分の差分法(英: Difference-in-Difference; DiD)があります。差分の差分法もパネルデータをもとに分析を行うことができます。パネルデータはこういった他の手法でもよく使われるデータ構造のため、データの取得段階でパネルデータの構造を持つように設計することや、複数のデータを組み合わせてパネルデータを作成することが因果推論では重要です。

参考文献#

目次