ロジスティック回帰モデル

ロジスティック回帰モデル#

このページでは、主に二値分類 (binary classification) で用いられる ロジスティック回帰モデル (logistic regression model) について解説します。

モデルの概要#

二値分類の問題で、説明変数 \(\mathbf{x}_i = (x_{i, 1}, \ldots, x_{i, K}) = (x_{i, k})_{k = 1}^K \in \mathbf{R}^K\) と目的変数 \(y_i \in \{0, 1\}\) たちの組に適合する分類モデルを学習したいものとします。ロジスティック回帰モデルでは、標準シグモイド関数（ロジスティック関数）

\[ \varsigma (\eta) = \frac{1}{1 + \exp (- \eta)} \]

を用いることで目的変数が1を取る条件付き確率

\[ p_i = P (y_i = 1 | \mathbf{x}_i) \]

を出力するようにします。標準シグモイド関数の値域は \(\eta \in \mathbf{R}\) に対して \(0 < \varsigma (\eta) < 1\) を満たすので、これを確率の値として扱うことができます。

具体的には、説明変数 \(\mathbf{x}_i\) の線形結合を標準シグモイド関数に入力して

\[\begin{split} \begin{align*} p_i & = \varsigma \left( b_0 + \sum_{k = 1}^K b_k x_{i, k} \right) \\ & = \frac{1}{1 + \exp \left( - b_0 - \sum_{k = 1}^K b_k x_{i, k} \right)} \end{align*} \end{split}\]

のように \(p_i \in (0, 1)\) を定めます。ここで \(\mathbf{b} = (b_k)_{k = 0}^K \in \mathbf{R}^{K + 1}\) はモデルのパラメータです。あとはこの \(p_i\) をベルヌーイ分布の成功確率として \(y_i | \mathbf{x}_i \sim \mathrm{Ber} (p_i)\) 、すなわち

\[\begin{split} y_i = \begin{cases} 0, & \text{with probability } (1 - p_i) \\ 1, & \text{with probability } p_i \end{cases} \end{split}\]

となるように統計モデルを仮定します。

なお、分野によってはロジスティック回帰モデルと同等のモデルを ロジットモデル (logit model) と呼んでいる場合があります。

モデルのパラメータの推定#

モデルのパラメータ \(\mathbf{b}\) の推定には最尤推定を用いることができます。訓練データ \(D = (\mathbf{x}_i, y_i)_{i = 1}^N\) が与えられたときの対数尤度 \(\ell (\mathbf{b}; D)\) は

\[\begin{split} \begin{align*} \ell (\mathbf{b}; D) & = \log \left( \prod_{i = 1}^N {p_i}^{y_i} {(1 - p_i)}^{1 - y_i} \right) \\ & = \sum_{i = 1}^N \left( y_i \log p_i + (1 - y_i) \log (1 - p_i) \right) \end{align*} \end{split}\]

となります。あとはこの対数尤度を \(\mathbf{b}\) について最大化して

\[ \hat{\mathbf{b}}_\text{MLE} = \arg \max_{\mathbf{b}} \ell (\mathbf{b}; D) \]

とすれば最尤推定量 \(\hat{\mathbf{b}}_\text{MLE} = (\hat{b}_{\text{MLE}, k})_{k = 0}^K\) を求めることができます。

なお、対数尤度 \(\ell (\mathbf{b}; D)\) は \(\mathbf{b}\) について上に凸であって最尤推定量 \(\hat{\mathbf{b}}_\text{MLE}\) も常に存在しますが、一般に解析的に書くことはできません。したがって実際に \(\hat{\mathbf{b}}_\text{MLE}\) を計算する場合は一般の非線形最適化手法によることになります。

推定したパラメータに基づく予測#

いま、モデルのパラメータを \(\hat{\mathbf{b}} = (\hat{b}_k)_{k = 0}^K\) と推定した上で、新しい説明変数 \(\mathbf{x}_\text{new} = (x_{\text{new}, k})_{k = 1}^K \in \mathbf{R}^K\) が与えられたものとします。このとき対応する目的変数 \(y_\text{new} \in \{0, 1\}\) が1の値を取る確率の予測値 \(\hat{p}_\text{new}\) は

\[\begin{split} \begin{align*} \hat{p}_\text{new} & = \varsigma \left( \hat{b}_0 + \sum_{k = 1}^K \hat{b}_k x_{\text{new}, k} \right) \\ & = \frac{1}{1 + \exp \left( - \hat{b}_0 - \sum_{k = 1}^K \hat{b}_k x_{\text{new}, k} \right)} \end{align*} \end{split}\]

と計算できます。また、必要があれば、目的変数の予測値 \(\hat{y}_\text{new}\) は

\[\begin{split} \hat{y}_\text{new} = \begin{cases} 0, & \hat{p}_\text{new} \le 0.5 \\ 1, & \hat{p}_\text{new} > 0.5 \end{cases} \end{split}\]

などによって求めることができます。

実装#

Pythonでロジスティック回帰を実装しているライブラリは複数ありますが、今回はその中でもscikit-learnとstatsmodelsを利用した実装例について簡単に解説します。

Hide code cell source 
# 解説の都合上、警告を発生させる必要があるため警告のフォーマットを変更
import warnings


def _custom_formatwarning(message, category, filename, lineno, line=None):
    """警告の表示でcategoryとmessageのみを記載するようにフォーマット"""
    s = f"{category.__name__}: {message}\n"
    return s


warnings.formatwarning = _custom_formatwarning

import numpy as np
import pandas as pd
import seaborn as sns
import sklearn
import statsmodels.api as sm

# import statsmodels.formula.api as smf


print(f"NumPy version: {np.__version__}")
print(f"pandas version: {pd.__version__}")
print(f"scikit-learn version: {sklearn.__version__}")
print(f"seaborn version: {sns.__version__}")
print(f"statsmodels version: {sm.__version__}")

NumPy version: 1.26.4
pandas version: 2.2.1
scikit-learn version: 1.4.1.post1
seaborn version: 0.13.2
statsmodels version: 0.14.1

データの準備#

本解説で用いるデータセットはscikit-learnに付属のwine datasetです。本来は3クラスの分類問題ですが、今回はそのうち2クラス分のデータのみを用いて二値分類の問題として扱います。また、説明変数についても解説の都合で本来13個あるうちの2個のみを用います。

from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split

data = load_wine(as_frame=True)  # 数値をpd.DataFrameなどに格納

print(f"Feature names: {data.feature_names}")  # 各説明変数の名前を表示
print(
    f"Target data counts: {data.target.value_counts().sort_index()}"
)  # 目的変数のクラスごとの個数を表示

Feature names: ['alcohol', 'malic_acid', 'ash', 'alcalinity_of_ash', 'magnesium', 'total_phenols', 'flavanoids', 'nonflavanoid_phenols', 'proanthocyanins', 'color_intensity', 'hue', 'od280/od315_of_diluted_wines', 'proline']
Target data counts: target
0    59
1    71
2    48
Name: count, dtype: int64

前述の通り、本解説ではこのデータセットの目的変数の3クラス 0, 1, 2 のうちの2クラス 0, 1 のみを用いて二値分類の問題として扱います。また、説明変数も 'ash', 'alcalinity_of_ash' の2つのみを用います。

X = data.data  # 説明変数を格納したpd.DataFrame
y = data.target  # 目的変数を格納したpd.Series

X = X[y != 2][["ash", "alcalinity_of_ash"]]
y = y[y != 2]

X.head()
ash alcalinity_of_ash
0 2.43 15.6
1 2.14 11.2
2 2.67 18.6
3 2.50 16.8
4 2.87 21.0 
y.head()

0    0
1    0
2    0
3    0
4    0
Name: target, dtype: int64

抽出したデータ全体の散布図を描くと次のようになります。

plot_data = pd.concat([X, y], axis=1)
sns.scatterplot(plot_data, x="ash", y="alcalinity_of_ash", hue="target")

<Axes: xlabel='ash', ylabel='alcalinity_of_ash'>
../_images/4e89370419fc5cbec507fa895747361b6aaba11274cf41d97e62c52f48d175f2.png

これらデータのうち8割を訓練用（ X_train, y_train ）とし、残りの2割を試験用（ X_test, y_test ）として分離しておきます。

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, random_state=42
)

scikit-learnでの実装#

scikit-learnにおいて、ロジスティック回帰モデルは LogisticRegression クラスに識別モデルとして実装されています。

from sklearn.linear_model import LogisticRegression

scikit-learnの LogisticRegression クラスはデフォルトで引数 penalty='l2' が設定されており、係数のL2正則化が行われます。係数の正則化を行わない場合は、明示的に引数 penalty=None を設定する必要があります。また、モデルのパラメータの最適化にはデフォルトでL-BFGS法（引数 solver='lbfgs' ）が指定されています。

clf = LogisticRegression(
    penalty=None,  # デフォルトでL2正則化が行われるのを（解説の都合で）無効化
    random_state=42,
    # solver='lbfgs',  # デフォルトでL-BFGS法が指定
)
clf.fit(X_train, y_train)  # 学習の実施

LogisticRegression(penalty=None, random_state=42)
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

学習したモデルの切片 \(\hat{b}_0\) と各説明変数に対応する係数 \((\hat{b}_k)_{k = 1}^K\) は次のように確認できます。

print(f"Intercept: {clf.intercept_}")  # 切片
print(f"Coefficients: {clf.coef_}")  # 係数

Intercept: [2.6643809]
Coefficients: [[-8.38912627  0.9333448 ]]

学習した識別モデルで予測を行う際には predict_proba() メソッドと predict() メソッドの2つが利用できます。このうち predict_proba() メソッドは目的変数の条件付き確率の予測値の組 \((1 - \hat{p}_i, \hat{p}_i)\) を返し、もうひとつの predict() メソッドは目的変数の予測値 \(\hat{y}_i\) を返します。

p_pred_sklearn = clf.predict_proba(X_test)
p_pred_sklearn[:5]  # 先頭の5サンプルについて表示

array([[0.23854037, 0.76145963],
       [0.83122234, 0.16877766],
       [0.99029096, 0.00970904],
       [0.33338193, 0.66661807],
       [0.01371823, 0.98628177]])

y_pred_sklearn = clf.predict(X_test)
y_pred_sklearn[:5]  # 先頭の5サンプルについて表示

array([1, 0, 0, 1, 1])

学習した識別モデルの評価には score() メソッドを使うことができます。 LogisticRegression クラスではaccuracy（正解率）が計算されます。

print(f"Training accuracy: {clf.score(X_train, y_train)}")
print(f"Test accuracy: {clf.score(X_test, y_test)}")

Training accuracy: 0.8942307692307693
Test accuracy: 0.7692307692307693

statsmodelsでの実装#

statsmodelsにおいて、ロジスティック回帰モデル（ロジットモデル）は Logit クラスとして実装されています。なお、formulaを利用してモデルを作成する場合は smf.logit() 関数を使うことができますが、こちらの詳細は省略します。

# import statsmodels.api as sm
# import statsmodels.formula.api as smf

statsmodelsではモデルの推論時に切片に対応するパラメータ \(b_0\) が考慮されないため、事前に add_constant() 関数を用いて説明変数にダミーの列 \(x_{i, 0} = 1\) を追加しておく必要があります。

Xarg_train = sm.tools.add_constant(X_train)
Xarg_test = sm.tools.add_constant(X_test)

Xarg_train.head()
const ash alcalinity_of_ash
70 1.0 2.21 20.4
78 1.0 1.95 14.8
47 1.0 2.12 16.0
0 1.0 2.43 15.6
12 1.0 2.41 16.0

たしかに説明変数のデータにダミーの列 'const' が追加されているのが確認できます。

この拡大したデータ Xarg_train, Xarg_test を用いてモデルの学習と検証を行います。 Logit のモデルのパラメータの最適化にはデフォルトでNewton-Rhapson法（引数 method='newton' ）が指定されています。

logit_mod = sm.Logit(
    y_train,
    Xarg_train,
)  # modelを作成（この時点では学習は行われない）
logit_res = logit_mod.fit(
    # method='newton',  # デフォルトでNewton-Rhapson法が指定
)  # fit()メソッドを実行すると学習の結果を格納したwrapperが返る

Optimization terminated successfully.
         Current function value: 0.296925
         Iterations 8

学習の結果はwrapper logit_res の中に格納されており、 summary() メソッドで概要を確認することができます。

print(logit_res.summary())

                           Logit Regression Results                           
==============================================================================
Dep. Variable:                 target   No. Observations:                  104
Model:                          Logit   Df Residuals:                      101
Method:                           MLE   Df Model:                            2
Date:                Mon, 01 Apr 2024   Pseudo R-squ.:                  0.5675
Time:                        14:44:11   Log-Likelihood:                -30.880
converged:                       True   LL-Null:                       -71.393
Covariance Type:            nonrobust   LLR p-value:                 2.543e-18
=====================================================================================
                        coef    std err          z      P>|z|      [0.025      0.975]
-------------------------------------------------------------------------------------
const                 2.6643      2.504      1.064      0.287      -2.243       7.572
ash                  -8.3892      1.688     -4.969      0.000     -11.698      -5.080
alcalinity_of_ash     0.9334      0.190      4.911      0.000       0.561       1.306
=====================================================================================

このうち、学習したモデルの切片 \(\hat{b}_0\) は下半分の数表のconst行のcoef列に、係数 \((\hat{b}_k)_{k = 1}^K\) はそれ以外の行のcoef列に表示されています。

学習したモデルで予測を行うにはwrapper logit_res の predict() メソッドを用いますが、これでは目的変数が1の値を取る条件付き確率 \(\hat{p}_i\) を出力します。

p_pred_sm = logit_res.predict(Xarg_test)
p_pred_sm[:5]

55     0.761461
40     0.168774
19     0.009709
31     0.666618
115    0.986282
dtype: float64

学習した識別モデルを（機械学習的な意味で）評価する関数はstatsmodelsには格納されていないので、NumPyなどの関数やメソッドで直接計算する必要があります。

print(
    f"Training accuracy: {((logit_res.predict(Xarg_train) > 0.5).astype(int) == y_train).astype(int).mean()}"
)
print(
    f"Test accuracy: {((logit_res.predict(Xarg_test) > 0.5).astype(int) == y_test).astype(int).mean()}"
)

Training accuracy: 0.8942307692307693
Test accuracy: 0.7692307692307693

モデルの解釈と応用#

この節ではロジスティック回帰モデルの解釈や他のモデルとの関係、それに関連する応用例などに関するいくつかの話題を解説します。

モデルの決定境界#

ロジスティック回帰モデルにおける決定境界 (decision boundary) の満たす条件は

\[\begin{split} \begin{align*} & p_i = 0.5 \\ \iff & \exp \left( - b_0 - \sum_{k = 1}^K b_k x_{i, k} \right) = 1 \\ \iff & b_0 + \sum_{k = 1}^K b_k x_{i, k} = 0 \end{align*} \end{split}\]

となります。したがって決定境界はモデルのパラメータ \(\mathbf{b} = (b_k)_{k = 0}^K\) が定める超平面（説明変数が2次元の場合は直線）になります。

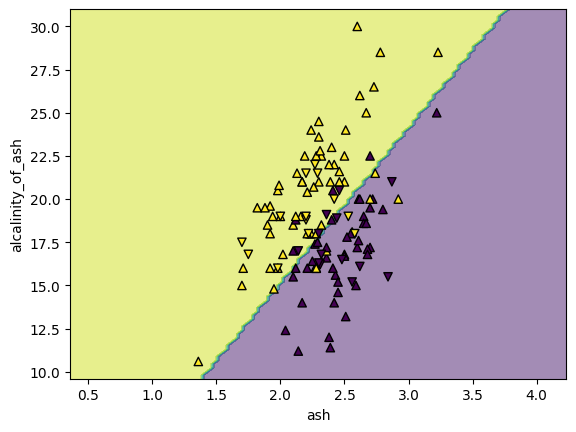
scikit-learnでは DecisionBoundaryDisplay クラスの from_estimator() メソッドを使うと学習済みのモデルからその決定境界を描画することができます。

from sklearn.inspection import DecisionBoundaryDisplay

disp = DecisionBoundaryDisplay.from_estimator(
    clf, X=X, response_method="predict", alpha=0.5
)  # 決定境界をプロット

disp.ax_.scatter(
    X_train.iloc[:, 0],
    X_train.iloc[:, 1],
    c=y_train,
    marker="^",
    edgecolor="k",
    label="train",
)  # 訓練データを上向き三角形でプロット
disp.ax_.scatter(
    X_test.iloc[:, 0],
    X_test.iloc[:, 1],
    c=y_test,
    marker="v",
    edgecolor="k",
    label="test",
)  # 試験データを下向き三角形でプロット

<matplotlib.collections.PathCollection at 0x32ed9ddc0>
../_images/378159ce3d7a7d00e3b6701eefc1db5de0fb18ea02a1e6e981397f0dffa2e96e.png

モデルの係数とオッズ比#

標準シグモイド関数（ロジスティック関数） \(\varsigma (\eta)\) の逆関数を ロジット関数 (logit function) といい、

\[ \mathrm{logit} ( q ) = \log \frac{q}{1 - q}, \quad 0 < q < 1 \]

の形で表現できます。この関数を用いてロジスティック回帰モデルの式を書き直すと

\[ \mathrm{logit} ( p_i ) = b_0 + \sum_{k = 1}^K b_k x_{i, k} \]

となります。ここで、左辺のロジット関数の中に出てくる

\[ \frac{p_i}{1 - p_i} \]

は目的変数 \(y_i\) が1の値を取る確率（事象 \(y_i = 1\) が発生する確率）と0の値を取る確率（事象 \(y_i = 1\) が発生しない確率）の比であり、しばしば オッズ (odds) と呼ばれます。

いま、説明変数 \(\mathbf{x}_i\) の特定の成分（特徴） \(x_{i, \kappa}\) だけが1単位だけ増加した \(\mathbf{x}'_i\) を

\[\begin{split} x'_{i, k} = \begin{cases} x_{i, k} + 1, & k = \kappa \\ x_{i, k}, & k \neq \kappa \end{cases} \end{split}\]

と定め、対応する条件付き確率を \(p'_i = P (y_i = 1 | \mathbf{x}'_i)\) とおくと

\[\begin{split} \begin{align*} \mathrm{logit} (p'_i) - \mathrm{logit} (p_i) & = b_\kappa (x_{i, \kappa} + 1) - b_\kappa x_{i, \kappa} \\ & = b_\kappa \end{align*} \end{split}\]

となります。したがって

\[\begin{split} \begin{align*} \exp (b_\kappa) & = \exp(\mathrm{logit} (p'_i) - \mathrm{logit} (p_i)) \\ & = \left(\frac{p'_i}{1 - p'_i}\right) / \left(\frac{p_i}{1 - p_i}\right) \end{align*} \end{split}\]

という関係が導けるため、係数 \(b_\kappa\) を指数関数で変換した \(\exp (b_\kappa)\) は「対応する説明変数の成分（特徴） \(x_{i, \kappa}\) が1だけ増加したときに、事象 \(y_i = 1\) が発生するオッズが比率の意味でどれだけ変化するか」を表していると解釈することができます。式の最後に現れたようなオッズの比率を オッズ比 (odds ratio) と呼びます。

今回学習したscikit-learnのモデルから計算されるオッズ比は次の通りです。

pd.Series(np.exp(clf.coef_.flatten()), index=X.columns, name="odds_ratio")

ash                  0.000227
alcalinity_of_ash    2.543001
Name: odds_ratio, dtype: float64

一般化線形モデルとの関係#

ロジスティック回帰モデルの式を書き直した

\[ \mathrm{logit} ( p_i ) = b_0 + \sum_{k = 1}^K b_k x_{i, k} \]

は、左辺と右辺がそれぞれ

  • 目的変数 \(y_i\) が従うベルヌーイ分布 \(\mathrm{Ber} (p_i)\) の未知パラメータ \(p_i\) をロジット関数で変換したものと

  • 説明変数 \((x_{i, k})_{k = 1}^K\) の線形結合

になっており、これらが等号で結ばれています。これは別項で解説する一般化線形モデル (generalized linear model) の一種になっています。

この側面から考えると、ロジスティック回帰モデルと同等のモデルは二値分類の問題だけでなく上限のあるカウントデータ（計数データ）の回帰問題にも利用できることがわかります。目的変数 \(y_i \in \{0, 1, \ldots, n_i\}\) が二項分布 \(\mathrm{B} (n_i, p_i)\) に従うと仮定します。そのパラメータのうち試行回数 \(n_i\) は既知とし、成功確率 \(p_i\) は説明変数 \(\mathbf{x}_i = (x_{k, i})_{k = 1}^K \in \mathbf{R}^K\) を用いて

\[\begin{split} p_i = \varsigma \left( b_0 + \sum_{k = 1}^K b_k x_{i, k} \right) \\ \end{split}\]

と表現できるものとします。やはり \(\mathbf{b} = (b_k)_{k = 0}^K \in \mathbf{R}^{K + 1}\) はモデルのパラメータです。このときの対数尤度 \(\ell_\mathrm{binom} (\mathbf{b}; D)\) は

\[ \ell_\mathrm{binom} (\mathbf{b}; D) = \sum_{i = 1}^N \left( \log \binom{n_i}{y_i} + y_i \log p_i + (n_i - y_i) \log (1 - p_i) \right) \]

となりますが、このうち \(\binom{n_i}{y_i}\) はパラメータ \(\mathbf{b}\) について定数です。したがって \(\mathbf{b}\) の最尤推定量 \(\hat{\mathbf{b}}_\text{MLE}\) は

\[\begin{split} \begin{align*} \hat{\mathbf{b}}_\text{MLE} & = \arg \max_{\mathbf{b}} \ell_\mathrm{binom} (\mathbf{b}; D) \\ & = \arg \max_{\mathbf{b}} \sum_{i = 1}^N \left( y_i \log p_i + (n_i - y_i) \log (1 - p_i) \right) \end{align*} \end{split}\]

となるため、この推定量は元々のカウントデータの標本 \((\mathbf{x}_i, y_i; n_i)\) が1個に対して二値分類の標本 \((\mathbf{x}_i, 1)\) が \(y_i\) 個、標本 \((\mathbf{x}_i, 0)\) が \((n_i - y_i)\) 個の合計 \(n_i\) 個を対応させた（二値分類の）ロジスティック回帰モデルを最尤推定した際の推定量と同じものになります。

多層パーセプトロンとの関係#

ロジスティック回帰モデルの式

\[\begin{split} p_i = \varsigma \left( b_0 + \sum_{k = 1}^K b_k x_{i, k} \right) \\ \end{split}\]

は、ニューラルネットワークの1ユニットで活性化関数を標準シグモイド関数 \(\varsigma( \cdot )\) とするものの出力を計算する式と同じ形をしています。特に、隠れ層のない（広義の）パーセプトロンで二値分類を行うモデルとは順伝播での数式上の表現が全く同じになります。

scikit-learnにおいて、 LogisticRegression クラスに実装されている最適化のソルバはL-BFGS法（引数 solver='lbfgs' で指定）やNewton-CG法（引数 solver='newton-cg' で指定）などのフルバッチを用いる手法のみとなっています。一般的なニューラルネットワークの学習のように確率的勾配降下法 (stochastic gradient descent; SGD) を用いた学習を行いたい場合、 代わりに SGDClassifier クラスを用いて引数 loss='log_loss' を指定してやる必要があります。ただし、 SGDClassifier には1標本ごとにパラメータ更新を行う古典的なSGDのみが実装されており、ミニバッチ学習には対応していません。

from sklearn.linear_model import SGDClassifier

clf_sgd = SGDClassifier(
    loss="log_loss",  # ロジスティック回帰モデルとして学習
    penalty=None,  # 係数の正則化を行わない
    max_iter=1000,  # 最大の反復回数
    random_state=42,
    learning_rate="constant",  # 定数の学習率を利用
    eta0=0.001,  # 初期の学習率を指定
    power_t=0.0,  # 学習率の減衰を行わない
    n_iter_no_change=1000,  # max_iterと同じ値を指定；訓練誤差の改善がない反復が続いても最大の反復回数まで学習を継続
)
clf_sgd.fit(X_train, y_train)

ConvergenceWarning: Maximum number of iteration reached before convergence. Consider increasing max_iter to improve the fit.

SGDClassifier(eta0=0.001, learning_rate='constant', loss='log_loss',
              n_iter_no_change=1000, penalty=None, power_t=0.0,
              random_state=42)
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

ここで ConvergenceWarning が出ているのは、今回の設定だと最大の反復回数 max_iter=1000 を終えた後でもパラメータが収束していないことを示しています。実用上は学習の設定を見直すか否かを検討すべき場面ですが、本解説では対応を省略します。

学習したモデルの切片や係数の値の確認、予測、評価などには LogisticRegression と同名の属性やメソッドを用いることができます。

print(f"Intercept: {clf_sgd.intercept_}")  # 切片
print(f"Coefficients: {clf_sgd.coef_}")  # 係数

Intercept: [-0.78532572]
Coefficients: [[-4.89691022  0.70027386]]

print(f"Training accuracy: {clf_sgd.score(X_train, y_train)}")
print(f"Test accuracy: {clf_sgd.score(X_test, y_test)}")

Training accuracy: 0.8365384615384616
Test accuracy: 0.7692307692307693

利用している最適化手法が大きく異なることもあり、学習した切片や係数の値は上記の LogisticRegression やstatsmodelsの Logit での例とやや違うものになっています。

小括#

このページでは、主に二値分類で用いられるロジスティック回帰モデルの概要について解説した上で、scikit-learnとstatsmodelsでの実装を紹介し、モデルの解釈や他のモデルとの関係についての話題にいくつか触れました。本解説ではデータの前処理（標準化など）やモデルの係数の正則化（L2正則化など）については省きましたが、実用上は必要になることの方が多いです。ロジスティック回帰モデルは二値分類を行う場合のベースラインとして利用されることも多いので、概要だけでも理解しておくと有益な場面があるかもしれません。

参考文献#

目次