Ctrl+K

プロセス制御とデータ分析

プロセス制御とデータ分析#

エアコン、冷蔵庫、洗濯機、PCに代表される身の回りのものから、反応器、撹拌機、ポンプなどプラントで用いられる大型のものまで、自動制御が行われています。特に石油・化学・電力・鉄鋼に代表される製造工程のように、原材料から製品ができるまで、連続したプロセスを対象とした制御をプロセス制御と呼びます。プロセス制御では、プラントの安定性はもちろんのこと、使用する原材料やエネルギー最小化まで、プロセスを最適に運転させることを目的としています。

本項では、特に工場のプロセス制御に着目し、その基礎知識とデータ分析の際に気を付けるべき点について解説します。

【解説すること】

  • プラントで収集されるプロセスデータの意味

  • フィードバック制御（特にPID制御）

  • 制御されている系のデータ分析

【解説しないこと】

  • 制御の詳細な理論

  • 制御系設計

本コンテンツの一連の分析でベースラインのデータセットとして用いている、酢酸ビニルプラントシミュレーター [Chen et al., 2003] のフロー図を以下に示します。

flow

このフロー図はP&ID（Piping and Instrumentation Diagram）図 と呼ばれ、設備や配管などの関係を表現するものです。この図では主に円筒状のものが設備、設備間をつなぐ線が配管を意味しています。各設備・配管には、分散型制御システム（Distributed Control System, DCS）で管理される制御器（コントローラー）が取り付けられており、それぞれの制御器は取得したセンサー情報に基づき自動制御を行います。

酢酸ビニルプラントシミュレーターで生成したデータを読み込みます。

import pandas as pd

df = pd.read_csv('../data/2020413.csv', index_col=0, parse_dates=True, encoding='cp932')
df.head(5)
気化器圧力_PV 気化器圧力_SV 気化器圧力_MV 気化器液面レベル_PV 気化器液面レベル_SV 気化器液面レベル_MV 気化器温度_PV 気化器ヒータ出口温度_PV 気化器ヒータ出口温度_SV 気化器ヒータ熱量_MV ... 反応器流入組成（CO2）_PV 反応器流入組成（C2H4）_PV 反応器流入組成（C2H6）_PV 反応器流入組成（VAc）_PV 反応器流入組成（H2O）_PV 反応器流入組成（HAc）_PV セパレータ蒸気排出量_MV (Fixed) アブソーバスクラブ流量_MV (Fixed) アブソーバ還流流量_MV (Fixed) 気化器液体流入量_MV (Fixed)
2020-04-13 00:00:00 127.983294 127.883920 18.728267 0.700204 0.7 21876.987772 120.159558 151.274003 150.0 9008.540694 ... 0.006273 0.585715 0.214016 0.001370 0.008524 0.109444 16.1026 15.1198 0.766 2.1924
2020-04-13 00:00:01 128.262272 127.807691 18.728267 0.700865 0.7 21876.987772 120.072575 151.218620 150.0 9008.540694 ... 0.006286 0.585342 0.213945 0.001368 0.008512 0.109441 16.1026 15.1198 0.766 2.1924
2020-04-13 00:00:02 127.899077 127.991074 19.079324 0.699740 0.7 21918.359526 120.305327 151.201067 150.0 8886.272509 ... 0.006281 0.584384 0.215043 0.001373 0.008541 0.109871 16.1026 15.1198 0.756 2.1924
2020-04-13 00:00:03 127.622218 127.990697 18.772228 0.699970 0.7 21892.166478 120.219488 151.220816 150.0 8806.115271 ... 0.006289 0.584467 0.214126 0.001372 0.008573 0.109775 16.1026 15.1198 0.746 2.1924
2020-04-13 00:00:04 127.577243 127.903788 18.605173 0.700939 0.7 21885.688813 120.302267 151.165624 150.0 8750.295310 ... 0.006313 0.584698 0.214002 0.001374 0.008547 0.109868 16.1026 15.1198 0.766 2.1924

5 rows × 91 columns

それぞれのカラムに装置名とその役割が示されています。ここでは記事執筆の便宜上、日本語の装置名がついていますが、一般には親切に日本語名がふられていることはなく、P&ID記号によって記述されます。
一般に「変量記号+機能記号+3桁装置番号」のようになっており、下に表記例と、よく使われる記号を示します。

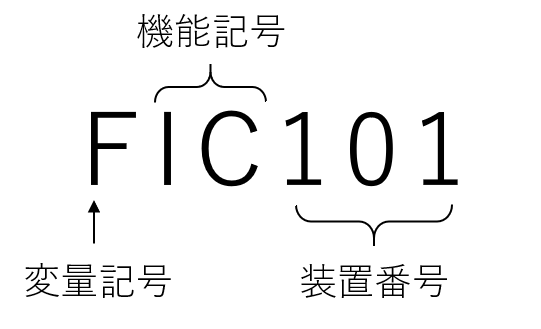
symbol

P&IDの記号とその意味

記号

変量記号

機能記号

A

濃度

警報

C

制御

F

流量

I

指示（測定値を表示）

L

レベル

P

圧力

Q

品質（組成）

T

温度

例えば、圧力指示制御器はPIC, 温度指示制御器はTICのように表されます。

次に、データのカラム名に注目すると 気化器圧力_PV, 気化器圧力_SV , 気化器圧力_MV のようにセットになっています。これは1つのフィードバックループで構成される制御器です。

フィードバック制御#

フィードバック制御では、制御対象の出力値（PV）と設定値（SV）との偏差に基づき、制御器が制御入力（MV）を決定します。ここでは1入力1出力（Single Input Single Output, SISO）の制御系を考えます。以下に示すのはブロック線図と呼ばれるフィードバック制御のフロー図です。

feedback

例として反応器温度の制御を考えます。目標値温度を120℃、プラントの現在の温度が100℃とし、制御器はヒーター熱量をコントロールできるとします（熱量を加えるとプラント温度が上がる）。目標値と出力値の偏差は20℃となり、制御器は20℃温度を上げるようにプラントに熱量を加えます。結果、プラントは新しい温度になり、これをフィードバックすることで再び目標値との偏差を計算、制御器が制御入力を決定します。以上を繰り返すことで出力値を目標値へと近づけていきます。

特にプロセス制御で用いられる用語を以下にまとめて示します。

  • プロセス変数（Process Variable, PV）

    • 制御対象の出力値。制御変数（Controlled Variable, CV）と言ったりもする

  • 操作変数（Manipulated Variable, MV）

    • プロセス変数を設定値に近づけるために、制御器が制御対象に入力する値（制御入力）

  • 設定値（Set Value, SV）

    • プロセス変数の目標値

  • 偏差（error, deviation）

    • プロセス変数と設定値の差（SV-PV）

  • 外乱（disturbance）

    • 制御系に影響を及ぼす外的要因（ノイズや観測できていない量）

つまり、前述の気化器圧力_PV, 気化器圧力_SV, 気化器圧力_MV はそれぞれ、「プロセス変数」「設定値」「操作変数」に対応します。

先ほど読み込んだデータからプロセス制御されている例を2つ可視化します。

import itertools
import matplotlib.pyplot as plt
from matplotlib.dates import DateFormatter

# matplotlibでは日本語にデフォルトで対応していないので、日本語対応フォントを読み込む
plt.rcParams['font.family'] = 'BIZ UDGothic' # Windows
# plt.rcParams['font.family'] = 'Hiragino Maru Gothic Pro' # Mac 

# その他使えるフォント一覧は以下のコードで取得できます。
# import matplotlib.font_manager
# [f.name for f in matplotlib.font_manager.fontManager.ttflist]

def plot_figs(df):
    '''
    受け取ったデータをすべてプロットする関数
    :param df: plotしたいpandas.Dataframe
    :return:
    '''
    color_iter = itertools.cycle(['#02A8F3', '#33B490', '#FF5151', '#B967C7'])
    n_figs = df.columns.size
    fig = plt.figure(figsize=(6, 2*n_figs), dpi=100)
    x = df.index
    for i in range(n_figs):
        y = df.iloc[:, i]
        title = df.columns[i]
        ax = fig.add_subplot(n_figs, 1, i+1)
        ax.plot(x, y, color=next(color_iter), linewidth=1.0)
        ax.xaxis.set_major_formatter(DateFormatter('%H:%M'))
        ax.set_xlim(x[0], x[-1])
        ax.set_title(title, fontsize=12)
    fig.tight_layout()
    plt.show()
    plt.close()

# 全部をプロットする余裕がないので、ここでは一部をプロット
plot_list = ['コンプレッサー出口温度_PV', 'コンプレッサー出口温度_SV', 'コンプレッサーヒーター熱量_MV', '気化器液面レベル_PV', '気化器液面レベル_SV', '気化器液面レベル_MV',]
plot_figs(df.loc[:, plot_list])
../_images/dad62998c70d5d09792490ca60fd9e224b3273497ad328686052452e37b49957.svg

まず、コンプレッサー出口温度 に着目すると、目標値（SV）が頻繁に切り替わっており、それに応じてプロセス変数（PV）が追従するように変化している様子が見て取れます。これは制御器によって操作変数（MV）が計算されているためです。ここで制御器は、温度制御を行うためにプラントに加える熱量を計算しています。

次に、気化器液面レベル を見てみると、SVが変化していないにも関わらず、9:00, 18:00ころにPVが変動しています。これは何かしらのプロセス外からの影響（外乱）があったためだと考えられます。しかし、PVは一度下がるもののしばらくすると元の値（平均値）に戻っています。これは制御器が適切なMVを計算し、外乱の影響を打ち消したためです。

本コンテンツでは扱いませんが、多くの化学プロセスでは、上位の制御器が下位の制御器の目標値を与えるような階層構造を持つカスケード制御が用いられる場合もあります。その場合には、タグ名が「_CSV, _CMV, CPV」のようにふられる場合が多いです。以下にカスケード接続のブロック線図を示します。例えば、ヒーターによって温度制御されている系を考えます。内側のループではヒーターの出力する熱量を一定にするように制御が行われます。一方、外側のループでは、温度が設定値に近づくように、ヒーターの設定値（内側のループ）を調整します。これにより、ヒーターに加わる外乱を抑制し安定した制御が可能となります。

cas

PID制御#

フィードバック制御の中でも、特に古典的で広く使用されているのがPID（Proportional-Integral-Derivative）制御です。例えば、石油化学プラントにおけるのPID制御, 古典的高度制御, モデル予測制御の比率は100:10:1と言われています [Kano et al., 2010]。
PID制御では以下の式に基づき、制御入力 \(u(t)\)が計算されます。

\[ u(t) = k_Pe(t) + k_I\int_0^t e(\tau)d\tau+k_D \frac{d}{dt}e(t) \]

ここで、\(e(t)\)は目標値（SV）と出力値（PV）の偏差で、\(k_P, k_I, k_D\)はそれぞれ制御器の特性を決定する比例定数です。それぞれの項について簡単に説明します。

  • 第1項: 比例項（Proportional term）

    • 偏差の定数倍（現在）

  • 第2項: 積分項（Integral term）

    • P制御だけだと定常偏差が発生してしまうので、偏差が存在し続ける限り\(u(t)\)を変化させ続ける（過去）。定常偏差が発生する理由の証明は「Pythonで学ぶ制御工学入門」のp.147を参照。

  • 第3項: 微分項（Derivative term）

    • より早く目標値に達するように、偏差の微分を用いる（未来）。例えば目標値が急に変わった場合には、偏差の微分値は大きくなり、\(u(t)\)も大きくなる。結果としてPIのみの場合よりもより大きい\(u(t)\)を制御対象に加えることができる。

以下に、P制御、PD制御、PID制御において、それぞれの定数を変化させ、制御を行った場合の例を示します。作図に用いたコードはページ末尾の付録を参照してください。

pid_control

横軸は時刻で、縦軸はプラントの出力値です。時刻0で初期値y=0のプラントに制御を行い、設定値y=30（黒線）に近づけた結果です。なお、このように時刻0で目標値が階段状に与えられる信号をステップ信号といいます。

この図から以下のことがわかります。

  • P制御において、\(k_P\)が大きくなると、立ち上がりが早くなり、振動の周期も早くなる（制御が振動的）。十分な時間がたっても目標値には到達しない（定常偏差, オフセット）

  • PD制御において、\(k_D\)を加えることで、振動が抑えられている。オフセットは改善されない。

  • PID制御において、定常偏差が改善され、目標値に収束している。

実際のプラントでも、比例定数\(k_P, k_I, k_D\)はプロセスの特性や所望する制御器の特性に合わせて調整をします。調整法としてはZiegler–Nichols (ZN) 法やChien, Hrones, Reswick (CHR) 法などが広く知られています。いずれの手法も目標値としてステップ信号を入力し、その応答（ステップ応答）をみることにより調整を行います。

しかし、実際に稼働中のプラントにおいて急激な目標値変化は安定性や経済性の観点から望ましいものではありません。つまり、制御パラメータの詳細なチューニングにはプロセスの応答特性が必要で、コストのかかるものになっています。
これを解決するため近年ではデータ駆動型制御器チューニング方法であるFRIT [相馬 et.al 2004] が提案されており、これは稼働中のプロセスのデータから制御器を設計するものです。

また古くから研究されている別のアプローチとして、システム同定があります。これはプラントの動特性をその入出力データ（蓄積されたデータ）からモデリングし、そのモデル上で制御設計を行うものです。システム同定についてはその手法やアイデアが機械学習分野にも通じる点が多々あるため簡単に紹介します。

システム同定（System Identification）#

モデリングは物理モデルと統計的モデルに大別されます。物理モデルでは、運動方程式や反応方程式などの対象を支配する原理に基づき、対象を微分方程式で表現します。物理モデルはその動特性を正確に把握できるためホワイトボックスモデルとも呼ばれます。重要な手法ですが、実際には複雑な現象を方程式に落とし込めなかったり、熱伝達率や触媒の活性化係数のように正確なパラメータを得ることが困難な場合があります。
一方で、統計的モデルに分類されるシステム同定は、前述のような現象に関する事前の知識を必要とせずプラントの入出力データからモデリングを行う手法です（ブラックボックスモデル）。複雑な系に対しても、入力データに対応する出力を比較的簡便に得られることがメリットです。一方でデータの質や、モデルの選択、パラメータチューニングによって、同定済みモデルの精度が変化してしまいます。
また、ホワイトボックスとブラックボックスを組み合わせたグレーボックスモデリングもあります。例えば、物理モデルを表す微分方程式のうち、未知パラメータだけをデータから推定します。ただし、個々の問題設定に依存するため一般的な理論はありません。

システム同定は、特に制御工学の分野で研究が盛んにおこなわれてきており、線形な手法については理論体系が完備されています。制御工学者御用達のMatlabではSystem Identification Toolbox に実装されています。PythonではSysIdentPy というライブラリがあるようです。

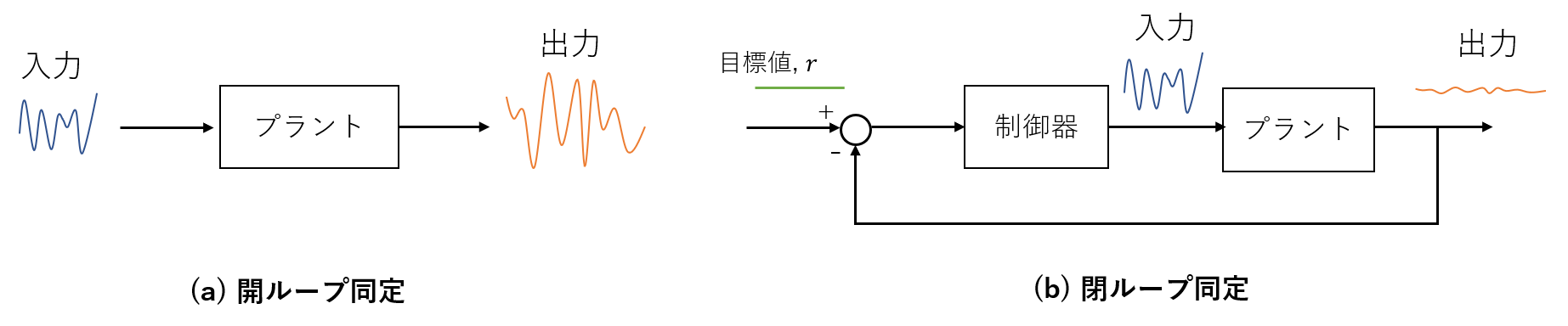
sysid

上図が示すように、システム同定は開ループ、閉ループがあります。いずれもプラントの入出力関係を使いますが、開ループの場合には制御器のことはいったん忘れ、任意の入力信号を使い対応する出力信号との関係からモデリングを行います。ただし、精度の良い同定のためには入力信号がプラントの動特性をうまく引き出せる性質のよい信号である必要があります（持続的励起性, 詳細は付録参照）。例えば、白色雑音はさまざまな周波数成分を含むためよいことが知られています。
一方、閉ループの場合には、制御器から生成される入力信号を用います。操業中のプラントから収集されるデータは一般には閉ループな問題になります。しかしながら、閉ループ同定は難しいことが知られています。極端な例として、フィードバック制御によって完璧に制御が行われている場合、設定値を変化させなければ出力値は一定で変化しません。したがって、入力（操作変数）が出力（制御変数）に与える影響を把握することができず、モデルを構築できないことになってしまいます。

モデル表現はノンパラメトリックでは相関解析法/周波数応答法/スペクトル解析法、パラメトリックではARXモデル/ARMAXモデル/Box-Jenkinsモデル/部分空間同定法などがあげられます。特にパラメトリックモデルのARX, ARMAXモデルは統計・機械学習分野ではよく用いられる時系列モデリング手法であり、入出力関係をうまく表現するパラメータを最小二乗法で推定することになります。

小括#

化学プロセスにおけるデータ分析の際に必要な基礎知識について紹介しました。化学プラントに代表される各種装置産業では、大規模なプロセス制御が行われており、そこから吸い上げられたデータをもとに分析作業を行います。
各データにはP&IDにもとづくタグが振られており、これを見れば何を意味しているかあたりを付けることができます。また、プロセス制御では多くの場合、PID制御にもとづくフィードバック制御が行われており、このためプラントの直接のモデリングは難しいことを簡単に解説しました。

参考文献#

  • [Chen et al., 2003] Chen R., Dave K., McAvoy T. J., and Luyben M. (2003). A nonlinear dynamic model of a vinyl acetate process. Industrial & engineering chemistry research, 42 (20), 4478-4487.

  • [Kano et al., 2010] M.Kano, and M.Ogawa (2010). The state of the art in chemical process control in Japan: Good practice and questionnare survey. Journal of Process Control, 20 (9), 969-982.

  • [相馬 et al., 2004] 相馬将太朗 金子修, 藤井隆雄 (2004). 一回の実験データに基づく制御器パラメータチューニングの新しいアプローチ--Fictitious Reference Iterative Tuningの提案, システム制御情報学会論文誌, 17 (12), 528-536.

  • 橋本伊織, 長谷部伸治, 加納学 (2020). 新版 プロセス制御工学. 朝倉出版.

  • 山本透 編 (2020). データ指向型PID制御. 森北出版.

  • 足立修一 (2009). システム同定の基礎. 東京電機大学出版局.

  • 南祐樹 (2019). Pythonで学ぶ制御工学入門. オーム社.

  • L. Ljung (1998). System Identification: Theory for the User. Pearson.

付録#

PID制御のコード#

本稿では、制御器の設計にPython-Control を用いました。このライブラリはMatlab Control System Toolboxと同様に制御システムの設計と解析が可能なライブラリです。
制御対象は、「Pythonで学ぶ制御工学入門」p.142で示される垂直駆動アームの角度制御とします。垂直に垂れさがったアーム（0°）に対して適切な制御を行い、目標角度30°にすることを考えます。詳細は前述の本を参照してください。 　この制御対象の微分方程式は、

\[ J \frac{d^2}{dt^2}y(t) + \mu \frac{d}{dt}y(t) + Mgly(t) = u(t) \]

であり、\(y(t)\)はアーム角度（制御出力）、 \(u(t)\)はアームに加わるトルク（制御入力）、 \(J\)は慣性モーメント、\(\mu\)は粘性係数、 \(M\)はアームの質量、 \(l\)はアームの長さ、 \(g\)は重力加速度です。

この制御対象の伝達関数モデル\(P(s)\)は、上式をラプラス変換して次のように表されます.

\[ P(s) = \frac{y(s)}{u(s)} = \mathcal{P}(s)=\frac{1}{Js^2+\mu s+Mgl} \]

また、制御器の伝達関数モデルは

\[ u(s) = \frac{k_D s^2 + k_P s + k_I}{s} e(s) \]

となります。これを実装したものが下記コードです。

import itertools
import control
from control import matlab
import matplotlib.pyplot as plt
import numpy as np

# 制御対象のパラメータ
g = 9.81    # 重力加速度
l = 0.2     # アーム長
M = 0.5     # アーム質量
mu = 1.5e-2 # 粘性係数
J = 1.0e-2  # 慣性モーメント

# 制御対象を伝達関数で表現
P = control.tf([0, 1], [J, mu, M*g*l])

# 目標値
ref = 30

# 作図用
fig = plt.figure(figsize=(14, 3.5) ,dpi=100)
ls_iter = itertools.cycle(['-', '--', '-.'])

# P制御
kps = [0.5, 1, 2] #パラメータ

ax1 = fig.add_subplot(131)
for kp in kps:
    K = matlab.tf([0, kp], [0, 1]) # P制御器
    Gyr = matlab.feedback(P*K, 1) # フィードバック制御系
    y, t = matlab.step(Gyr, np.arange(0, 4, 0.001))
    ax1.plot(t, y*ref, ls=next(ls_iter), label=f'$k_P=${kp}')
ax1.hlines(ref, 0, 4, color='k', linewidth=0.5)
ax1.legend()
ax1.set_xlabel('t')
ax1.set_ylabel('y')
ax1.set_title('P')
ax1.grid(ls=':')


# PD制御
kp = 2
kds = [0, 0.1, 0.2] # パラメータ

ax2 = fig.add_subplot(132)
for kd in kds:
    K = matlab.tf([kd, kp], [0, 1]) # PD制御器
    Gyr = matlab.feedback(P*K, 1) # フィードバック制御系
    y, t = matlab.step(Gyr, np.arange(0, 2, 0.001))
    ax2.plot(t, y*ref, ls=next(ls_iter), label=f'$k_D=${kd}')
ax2.hlines(ref, 0, 2, color='k', linewidth=0.5)
ax2.legend()
ax2.set_xlabel('t')
ax2.set_ylabel('y')
ax2.set_title('PD')
ax2.grid(ls=':')

# PID制御
ax3 = fig.add_subplot(133)
kp = 2
kd = 0.1
kis = (0, 5, 10)

for ki in kis:
    K = matlab.tf([kd, kp, ki], [1, 0]) # PID制御 K = kd * s + kp + ki/s
    Gyr = matlab.feedback(P * K, 1)
    y, t = matlab.step(Gyr, np.arange(0, 2, 0.01))
    ax3.plot(t, y*ref, ls=next(ls_iter), label=f'$k_I=${ki}')
ax3.hlines(ref, 0, 2, color='k', linewidth=0.5)
ax3.legend()
ax3.set_xlabel('t')
ax3.set_ylabel('y')
ax3.set_title('PID')
ax3.grid(ls=':')

fig.tight_layout()
# plt.savefig('image/pid_control.png')
# plt.show()
../_images/d8194accf1b4cf3233df89372561613fa1753731f0fb28b5614a5381e6fb41f0.svg

持続的励起性#

持続的励起性（Persitently Exciting, PE性） とは同定のための入力信号が、最低限満たしていなければならない条件のことです。

1入力1出力離散時間のARXモデルを考えます。出力\(y\), 入力\(u\), ノイズ\(w\), 離散時間\(k\), モデルパラメータ\(a, b\) です。

\[ y(k)= -a_1 y(k-1) - \cdots - a_{n_a} y(k-n_a) + b_1 u(k-1) + \cdots + b_{n_b} u(k-n_b) + w(k) \tag{1} \]

余談ですが、制御工学の分野では、次のような伝達関数表現を利用する場合が多いです。

\[\begin{split} A(q)y(k) = B(q)u(k) + w(k) \\ y(k) = \frac{B(q)}{A(q)} u(k) + \frac{1}{A(q)} w(k) \\ A(q) = 1 + a_1 q^{-1} +\cdots + a_{n_a}q^{-n_a} \\ B(q) = b_1 q^{-1} + \cdots + b_{n_b}q^{-n_b} \end{split}\]

\(q^{-1}\)は遅延演算子で、\(q^{-1}x(k)=x(k-1)\)を意味します。

システム同定において、求めたいのは最適なパラメータ\(a_1,\cdots, a_{n_a}, b_1, \cdots, b_{n_b}\)であるので、(1)式において

\[\begin{split} \mathbf{\theta} = \left[a_1,\cdots, a_{n_a}, b_1, \cdots, b_{n_b} \right]^T \\ \mathbf{\phi}(k) = \left[-y(k-1), \cdots, -y(k-n_a), u(k-1), \cdots, u(k-n_b) \right] \end{split}\]

とおけば、予測誤差\(\varepsilon\)は次式で表されます。

\[ \varepsilon(k) = y(k) - \hat{y}(k) = y(k) - \mathbf{\phi}(k)\mathbf{\theta} \]

したがって、予測誤差の分散（二乗和）は

\[ J(\mathbf{\theta}) = ||\varepsilon||^2 = ||\mathbf{y} - \mathbf{\Phi\theta}|| \]

であり、最小二乗法より、この評価関数を最小化するパラメータ\(\theta\)は次のように求まります。

\[ \mathbf{\theta} = (\Phi^T\Phi)^{-1}\Phi^T y　\tag{2} \]

システム同定においては、パラメータの数（\(n_a, n_b\)）は自分で設定することになり、パラメータ数が多いほどより複雑な系を表現することができます。

ここで、(2)式を計算するためには、行列\(\Phi^T\Phi\)が正則である必要があります。つまり、求められるパラメータ数の次数はこの行列のランクに一致します。逆に言うとn個のパラメータで表現される系を同定するためには、\(n\ge n_a+n_b\)である必要があり、性質のいい入出力関係がないと同定することが難しいことがわかります。特に、この次数のことをPE性の次数といいます。
ただしあくまでも最低条件なので、実用上はより多くの周波数成分を含んだ性質のいい信号が望ましいです。

余談#

「システム同定の基礎」p.76では「\(n\)次系を同定するためには、入力信号は次数\(2n\)のPE性信号でなければならない」とありますが、本記事では 「System Identification: Theory For The User」「新版プロセス制御工学」に従い、必要なPE性の次数については\(n_a+n_b\)としています。

目次