カルマンフィルタ#

はじめに#

この記事ではカルマンフィルタについて解説します。フィルタと聞くと、エアコンやコーヒーのフィルタを彷彿とさせるかもしれません。フィルタとは一般的に対象から不純物を濾し取り、必要な成分だけを抽出するもののことを指し、時系列データにも同様に観測したデータから必要なデータのみ取り出す機能として使われます。例えば時系列データに対して使われる代表的なフィルタの例として、ハイパスフィルタ、ローパスフィルタがあります。これらは特定の周波数領域上にあるデータを抽出するために使われ、上記のフィルタの定義と合致します。またウィナーフィルタのように伝達関数を用いて雑音を除去し真の信号を得る手法もあります。このように、その時刻までに得られた測定データ中に含まれている雑音を除去し、真の信号を得る手法を模索することを古典的フィルタリング問題といいます。

一方この記事で紹介するカルマンフィルタは観測データから状態空間モデルに基づいてシステム内部の状態を推定するフィルタです。状態空間モデルを上手く設計し利用することで、1つもしくは複数の観測データや入力データから確率的な変動を取り入れながら正確なデータを推定できます。これはその時刻までに得られた測定データや(必要であれば)システムの入力データを使って動的システムの状態の値を推定する手法を模索する状態推定問題の代表的な手法です。古典的フィルタリング問題と比較して真の信号を得るものと思えば似ていますが、システムのダイナミクスを考慮して内部の状態を推定するという点に違いがあります。状態空間モデルを使うことから分かるようにカルマンフィルタはシステム制御理論から発展してきた手法ですが、制御分野だけでなく気象予測、金融、水産、土木等さまざまな分野で使われています。本稿ではカルマンフィルタを使うことで何ができるか、そのアルゴリズムの原理を説明していきます。またアルゴリズムの項では、簡潔な説明のため式の導出については省略しているものがあります。導出部分が気になる場合は、最後に記載してある参考文献を参考にしてみてください。

状態空間モデルと状態推定問題#

状態空間モデルとは#

カルマンフィルタを理解する前にまず状態空間モデルと状態推定問題について理解する必要があります。

状態空間モデルとはシステムのモデルを行列やベクトルで表現したものであり、状態空間表現とも呼びます。実際に具体例を見ながら状態空間モデルについて理解していきます。

よく例えに使われる1次元のバネ-マス-ダンパ系を考えます。古典物理学により、下の図にあるような物体の位置と力の関係を運動方程式と呼ばれる微分方程式により記述されることが知られています。下の図は以下の運動方程式に従って質量\(M\)の物体に加わる力を表しています。物体は粘性(減衰)係数\(C\)のダンパ、バネ定数\(K\)のバネに繋がっており、外力\(u_t\)が加わっています。また物体は連続的に位置\(y_t\)が時間変化します。ここで\(u_t\)をシステムの入力、\(y_t\)をシステムの出力(スカラの場合は観測値、ベクトルの場合は観測ベクトルとも呼ぶ)と呼ぶことにします。

\[ \begin{align*} M \ddot{y_t} + C \dot{y_t} + K y_t = u_t \end{align*} \]

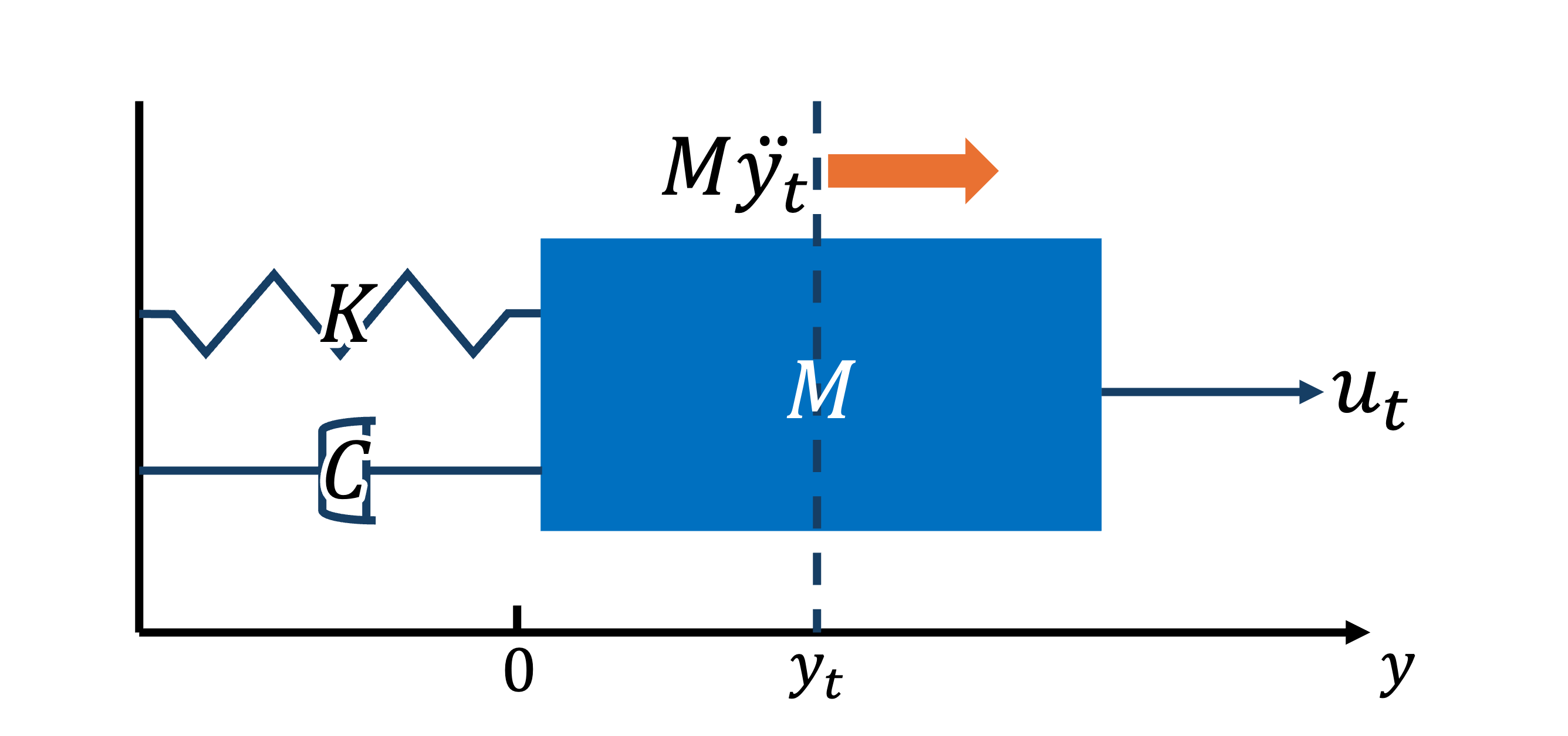
spring_object_damper

このような微分方程式で記述される力学的な関係をダイナミクスと呼び、連続時間系だと微分方程式、離散時関系だと差分方程式で記述されます。

ここで位置\(y_t\)と速度\(\dot{y_t} \)を以下のようにベクトル\({x}_t\)の成分で表します。このベクトル\({x}_t\)を状態ベクトル、状態ベクトルのそれぞれの成分のことを状態変数と呼び、ここでは\(x_{t,1} \)、\(x_{t,2}\)として定義します。また状態変数が1つしかない場合や状態ベクトル\({x}_t\)そのものを単純に状態と呼ぶこともあります。

\[\begin{split} \begin{equation*} {x}_t = \begin{bmatrix} x_{t,1} \\ x_{t,2} \\ \end{bmatrix} = \begin{bmatrix} y_t \\ \dot{y_t} \\ \end{bmatrix} \end{equation*} \end{split}\]

この時\( x_{t,1} \)と\(x_{t,2}\)の間には\( x_{t, 2} = \dot{x}_{t, 1} \)が成り立ちます。

運動方程式に代入し、整理すると以下の式となります。

\[ \begin{equation*} \dot{x}_{t, 2} = \frac{1}{M}\{- C {x_{t, 2}} - K {x_{t, 1}} + u_t\} \end{equation*} \]

これらの式から\(x_{t, 1}\)と\(x_{t, 2}\)に関する連立方程式を立てると以下のようになります。

\[\begin{split} \begin{align*} \begin{bmatrix} \dot{x}_{t, 1} \\ \dot{x}_{t, 2} \end{bmatrix} \ = \begin{bmatrix} 0 & 1 \\ -\cfrac{K}{M} & -\cfrac{C}{M} \end{bmatrix} \ \begin{bmatrix} x_{t, 1} \\ x_{t, 2} \end{bmatrix} + \begin{bmatrix} 0 \\ \cfrac{1}{M} \end{bmatrix} u_t \end{align*} \end{split}\]

ここで

\[\begin{split} \begin{align*} A = \begin{bmatrix} 0 & 1 \\ -\cfrac{K}{M} & -\cfrac{C}{M} \end{bmatrix} ,\ {b} = \begin{bmatrix} 0 \\ \cfrac{1}{M} \end{bmatrix} \ \end{align*} \end{split}\]

と置くと

\[ \begin{align*} \dot{{x}}_t = A {x}_t + {b} u_t \end{align*} \]

と表せ、これを状態方程式と呼び、動的システムを状態ベクトルによって記述します。また行列\(A\)を遷移行列と呼びます。

また\(y_{t} = {x}_{t, 1}\)より、状態ベクトル\({x}_t\)と組み合わせ\(y_t\)は以下のように表せます。

\[ \begin{align*} y_{t} = {{c}} {{x}}_t, ~{{c}} = \begin{bmatrix} 1\ 0 \end{bmatrix} \end{align*} \]

これを観測方程式と呼び、この式はシステム内部の状態と観測値(出力)との関係を表現しています。ベクトル\( {c}\)のことを観測行列(今回の例ではベクトルですが)と呼びます。

この状態方程式と観測方程式の連立方程式からシステムを記述できるのが状態空間モデルです。システム内部の変数である状態ベクトルを表現できるのが最大の特徴であり、これはシステムの入力と出力を媒介し、システムの振る舞いを記述する重要なファクターです。

伝達関数も同じようにシステムを表現できますが、入力と出力というシステムの外部で観測される変数から1入力1出力のシステムしか記述できません。今回の例で言う位置や速度といったシステム内部の状態ベクトルを考慮した操作は一切できません。一方状態空間モデルでは(今回の例では1入力1出力でしたが)多入力多出力のシステムを記述でき、状態方程式と観測方程式さえ上手く設計できれば、内部の状態ベクトルを考慮したシミュレーション等を行うことができます。 この直接観測できない状態ベクトルを求めることがカルマンフィルタを用いる主な目的の1つでもあります。また状態空間モデルから伝達関数には一意的に変換できる一方、逆は一意的には変換できません。

ただし遷移行列\(A\)や\( {b}\)など状態空間モデルを構成する各係数行列を求めること(設計とも呼ぶ)はシステムのダイナミクスを正確に把握する必要があり、システムの入力と出力のデータから各係数行列を求めるのは一般的には大変難しいとされています。この過程をシステム同定と呼びますが、本記事の主旨から逸脱するためこの記事では各係数行列は既知のものとして説明します。

ここまでは連続時間系での状態空間モデルの記述について説明しましたが、実際に計算機上のプログラムで状態空間モデルを取り扱う場合やこの後のカルマンフィルタの説明では離散時間系を前提とすることが多いです。以下の図のように実世界のシステム上の連続時間信号\(y_t \ (0 \leq t < \infty)\)上のデータを一定間隔(サンプリング周期)\(\Delta t\)でサンプリングして離散時間信号\(y_k \ (k=0, 1, 2, \dotsc)\)に変換します。

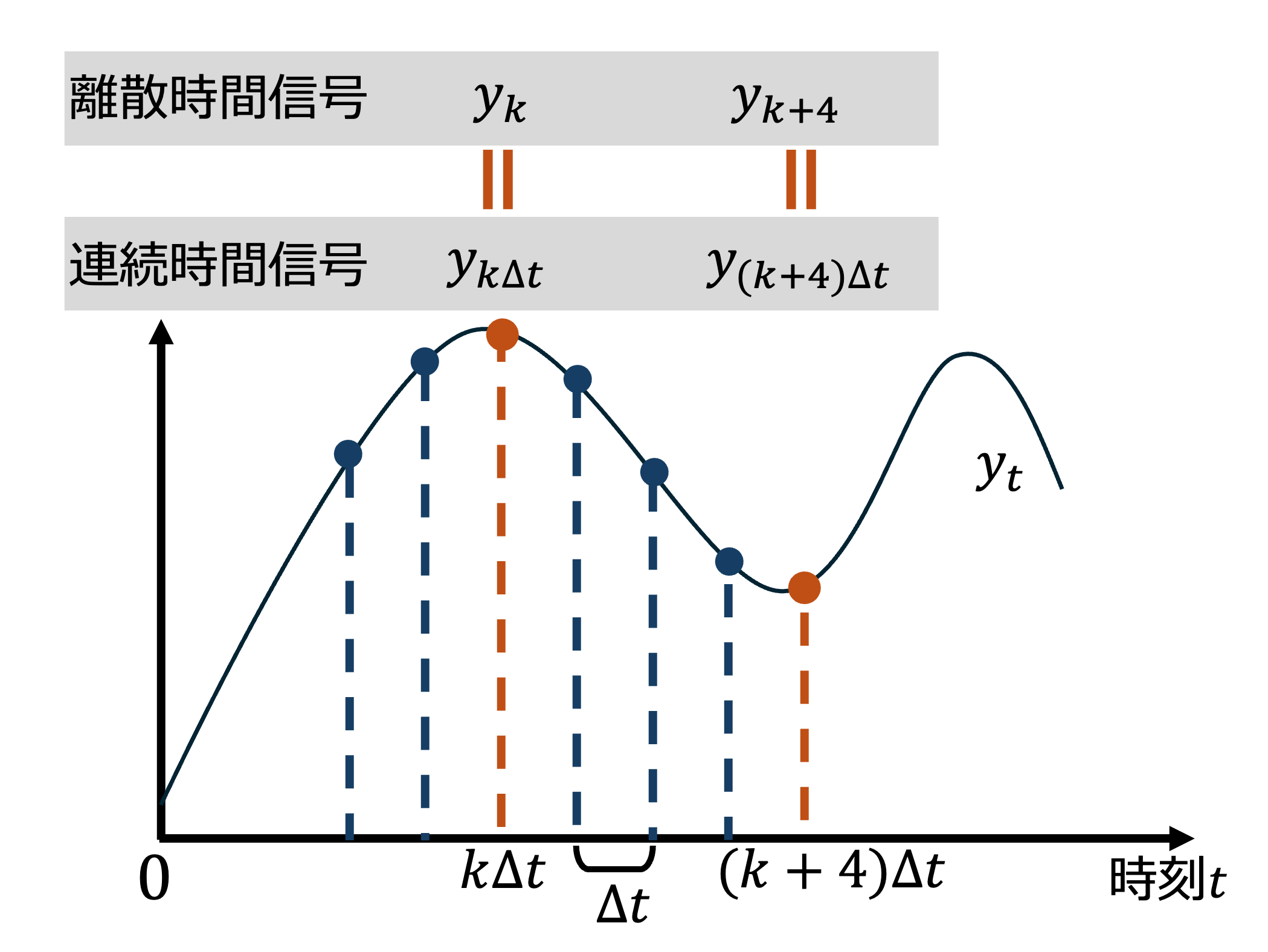
spring_object_damper

離散時間系の状態空間モデルも連続時間系の状態空間モデルとは表現が異なり、連続時間\(t\)が離散時間(ステップ)\(k\)に置き換わり、微分方程式が差分方程式で表現されるのが大きな違いです。上の例で挙げた連続時間系の状態空間モデルを離散時間系で表現すると次式のようになります。基本的な形は連続時間系での状態空間モデルとは大きく変わりませんが、状態方程式の左辺は\(k+1\)ステップ目の状態ベクトル(この場合だと状態ベクトル)\({x}_{k+1} \)となるのが一般的な形となります。

\[\begin{split} \begin{align*} {x}_{k+1} &= F {x}_{k} + {d} u_k　&状態方程式 \\ y_{k} &= {h} {x}_{k}　&観測方程式 \\ \end{align*} \end{split}\]

\( {x}_{k} : \) 状態ベクトル
\( y_{k} : \) 観測値
\( F : \) 遷移行列
\( {h} \) : 観測行列

連続時間系、離散時間系それぞれの状態空間モデルの式を見て分かるように、それぞれの係数行列はそのままでは一致しませんが以下の厳密解を求めることで変換は可能です。導出は割愛しますが、それぞれの係数行列は以下のように求まります。 \(\Delta \text{t}\)はサンプリング幅です。

\[\begin{split} \begin{array}{rl} F &= e^{A \Delta \text{t}} \\ {d} &= A^{-1} (e^{A \Delta \text{t}} - I) {b} \\ {h} &= {c} \\ \end{array} \end{split}\]

非線形システムの場合、局所線形化等を用いて\(e^{A \Delta \text{t}}\)を高い精度で求めることは可能ですが、線形化する度に\(e^{A \Delta \text{t}}\)を計算するのは計算コストが高いことがあります。一方Euler法などを用いれば更に低い計算コストで近似解を求めることができ、状況によってはこの近似解で精度的には十分な場合もあります。

更に係数行列が時間変化したり、多入力多出力システムに対応したりとこの離散時間系の状態空間モデルをより一般化させると以下のような形となります。

\[\begin{split} \begin{align*} {x}_{k+1} &= F_k {x}_{k} + D_k {u}_{k}　&状態方程式 \\ {y_{k}} &= H_k {x}_{k}　&観測方程式 \\ \end{align*} \end{split}\]

\( {x}_{k} : \) 状態ベクトル
\( {y_{k}} : \) 観測ベクトル
\( F_k : \) 遷移行列
\( H_k : \) 観測行列

以下の説明では離散時間系での変数または状態空間モデルを前提として説明します。

状態推定問題#

以上状態空間モデルについて説明しましたが、状態空間モデルを用いることでシステムのダイナミクスを記述できるだけでなく、本来は観測できない内部の状態ベクトルを扱うことができることが分かりました。状態空間モデルを使って状態ベクトルそのものを観測データから求める代表的な手法としてはオブザーバ(状態観測器)があります。しかしオブザーバは状態空間モデルの各方程式に雑音を考慮しないアルゴリズムであり、現実のシステムや収集されるデータには不規則雑音が介在しているケースが多く、現実のシステムにノイズが介在しないという条件でないと上手く推定できないことがあります。一方カルマンフィルタは同じように状態空間モデルを利用しつつ、雑音を考慮したアルゴリズムであるため、モデルさえ予めうまく構築出来ていれば高い精度で状態を推定できます。

バネ-マス-ダンパ系の例のようにシステムのダイナミクスが明らかであるという仮定の元、不規則雑音の影響下にある観測値\({y_1, \cdots, y_k}\)から推定された状態ベクトルの推定値と真の状態ベクトルとの推定誤差\(e_k\)のノルム\(\lVert e_k \rVert\)を最小にするような推定値を求める問題を状態推定問題と呼びます。また上のバネ-マス-ダンパ系の例のように加えた力しかデータが手元にない状況で、直接測定できない位置や速度をモデルから推定するカルマンフィルタ含めたアルゴリズム全般をソフトセンサと呼びます。

不規則雑音の影響下にあるシステムの状態空間モデルは以下のように記述されます。カルマンフィルタはこのような雑音を含んだ状態空間モデルを用いて状態推定問題を解きます。

\[\begin{split} \begin{align*} {x}_{k+1} &= F_k {x}_{k} + D_k {u}_k + G_k {w}_k&状態方程式 \\ {y_{k}} &= H_k {x}_{k} + {v}_k &観測方程式 \\ \end{align*} \end{split}\]

\( {x}_{k} : \) 状態ベクトル
\( {y_{k}} : \) 観測ベクトル
\( w_k: \) システム雑音
\( v_k : \) 観測雑音
\( F_k : \) 遷移行列
\( D_k : \) 入力行列
\( G_k : \) 駆動行列
\( H_k : \) 観測行列

状態方程式、観測方程式ともに雑音を含み、これらが何かしらかの確率分布に従っている場合、\({x}_{k}\)、\({y_{k}} \)もともに確率変数となります。この時雑音が正規性白色雑音のときガウス状態空間モデル、式がこのように線形だと線形状態空間モデルと呼び、最も基本的な状態空間モデルとなります。一方雑音が非正規性だったり、状態空間モデルの式が非線形だったりする場合、非ガウス・非線形状態空間モデルと呼びます。現実のシステムは非正規性や非線形性を持つことも多いですが、この場合より高度なカルマンフィルタや非正規性ノイズの近似等複雑なプロセスが必要となります。これ以降の説明では最も一般的な形であるガウス・線形状態空間モデルを前提として説明します。また本記事では説明の簡略化のため、以降は状態方程式の入力項\(D_k {u}_k\)は省略して説明します。

このような推定問題は収集された観測値(もしくは観測ベクトル)の時刻\(k\)と推定する状態の時刻\(s\)との大小関係のよって以下の3つに分類されます。

予測(Prediction)問題 \((s > k)\)
時刻\(k\)までの観測ベクトル\(y_k\)を用いて未来の時刻\(s\)の状態ベクトル\({x}_s \)を推定する問題
フィルタリング(Filtering)問題 \((s = k)\)
時刻\(k\)までの観測ベクトル\(y_k\)を用いて同じ時刻\(s\)の状態ベクトル\({x}_s \)を推定する問題
平滑(smoothing)問題 \((s < k)\)
時刻\(k\)までの観測ベクトル\(y_k\)を用いて過去の時刻\(s\)の状態ベクトル\({x}_s \)を推定する問題

本記事のカルマンフィルタはフィルタリング問題を扱います。

カルマンフィルタとは#

以上のように状態ベクトル\(x_k\)との誤差ノルムが最小となる推定値を求めることが状態推定問題と説明しました。 カルマンフィルタは状態空間モデルを用いて、特に状態空間モデル中の各変数がガウス分布(正規分布)に従っている場合の状態推定問題に用いられる代表的な手法です。簡単に言うと時刻\(k\)において、前の時刻\(k-1\)の状態推定値と\(k\)の観測値\(y_k\)(と必要であればシステムへの入力\(u_k\))から\(x_k\)の推定値を求め、これを各時刻において逐次的に行います。そして各時刻における推定は　1. 予測ステップ 2. 観測更新ステップ と呼ばれる2つのステップからなります。

次のような1変数の観測値\({y}_{k}\)と1変数の状態\({x}_{k}\)を組み込んだ状態空間モデルを例にカルマンフィルタの流れについて説明します。

\[\begin{split} \begin{align*} {x}_{k+1} &= F_k{x}_{k} + G_k{w}_k&状態方程式 \\ {y_{k}} &= H_k{x}_{k} +{v}_k &観測方程式 \\ \end{align*} \end{split}\]

\( {x}_{k} : \) 状態
\( {y_{k}} : \) 観測値
\( w_k: \) システム雑音(正規性白色雑音)
\( v_k : \) 観測雑音(正規性白色雑音)
\( F_k : \) 遷移行列
\( G_k : \) 駆動行列
\( H_k : \) 観測行列

このようにシステムには正規性白色雑音が混入しています。このような線形状態空間モデルでは観測値\({y}_{k}\)と状態\({x}_{k}\)はガウス分布の再生性により正規性が保存され、観測値\({y}_{k}\)と状態\({x}_{k}\)がガウス分布に従い続けます。これはカルマンフィルタを用いる上で重要な性質です。カルマンフィルタは状態 \(x_k\) がガウス分布に従うという仮定のもとで、そのガウス分布の期待値と共分散行列を逐次的に推定します。

ここで状態の推定分布を予測分布とフィルタ分布の2つの言葉に分けて定義します。時刻\(k\)における 予測分布(事前推定分布とも呼ぶ) とは時刻\(k-1 \)までの観測値を用いて推定した\(x_k\)の分布のことです。予測分布の期待値(事前推定値とも呼ぶ)を\(\hat{x}_{k | k-1}\)、共分散行列(事前共分散行列とも呼ぶ)を\(P_{k | k-1}\)と表現します。また時刻\(k\)における フィルタ分布(事後推定分布とも呼ぶ) とは時刻\(k\)で推定した予測分布に加え、観測値\(y_k\)も用いて推定した状態\(x_k \)の分布のことを指します。フィルタ分布の期待値(事後推定値とも呼ぶ)を\(\hat{x}_{𝑘 | 𝑘}\)、共分散行列(事後共分散行列とも呼ぶ)を\(P_{k | k}\)と表現します。このフィルタ分布の期待値\(\hat{x}_{𝑘 | 𝑘}\)が最終的に求めたい状態\(x_k\)の状態推定値となります。

時刻\(k\)の予測分布は予測ステップ、時刻\(k\)のフィルタ分布は観測更新ステップで求められます。まず予測ステップにて\(𝑘−1\)で求めたフィルタ分布とモデルを使って\(𝑘\)の予測分布の期待値\(\hat{x}_{k | k-1}\)、共分散行列\(P_{k | k-1}\)を求めます。次に観測更新ステップによって予測分布と観測値\(𝑦_𝑘\)から時刻\(𝑘\)のフィルタ分布の期待値\(\hat{𝑥}_{𝑘|𝑘}\)と共分散行列を求めます。先ほど述べたようにこのフィルタ分布の期待値\(\hat{𝑥}_{𝑘|𝑘}\)こそが、求めたい\(x_k\)の状態推定値です。観測更新ステップにおいて\(\hat{𝑥}_{𝑘|𝑘}\)は観測値\(y_k\)と推定した\(\hat{y}_{𝑘}\)との誤差に係数をかけて、予測分布の期待値\(\hat{x}_{k | k-1}\)を足し合わせることで得ることができますが、この係数をカルマンゲインと呼びます。カルマンゲインはステップごとに大きさが変化しますが、その詳細についてはこの後に説明します。ここで述べた予測ステップと観測更新ステップの大まかな流れは以下の図の通りになります。

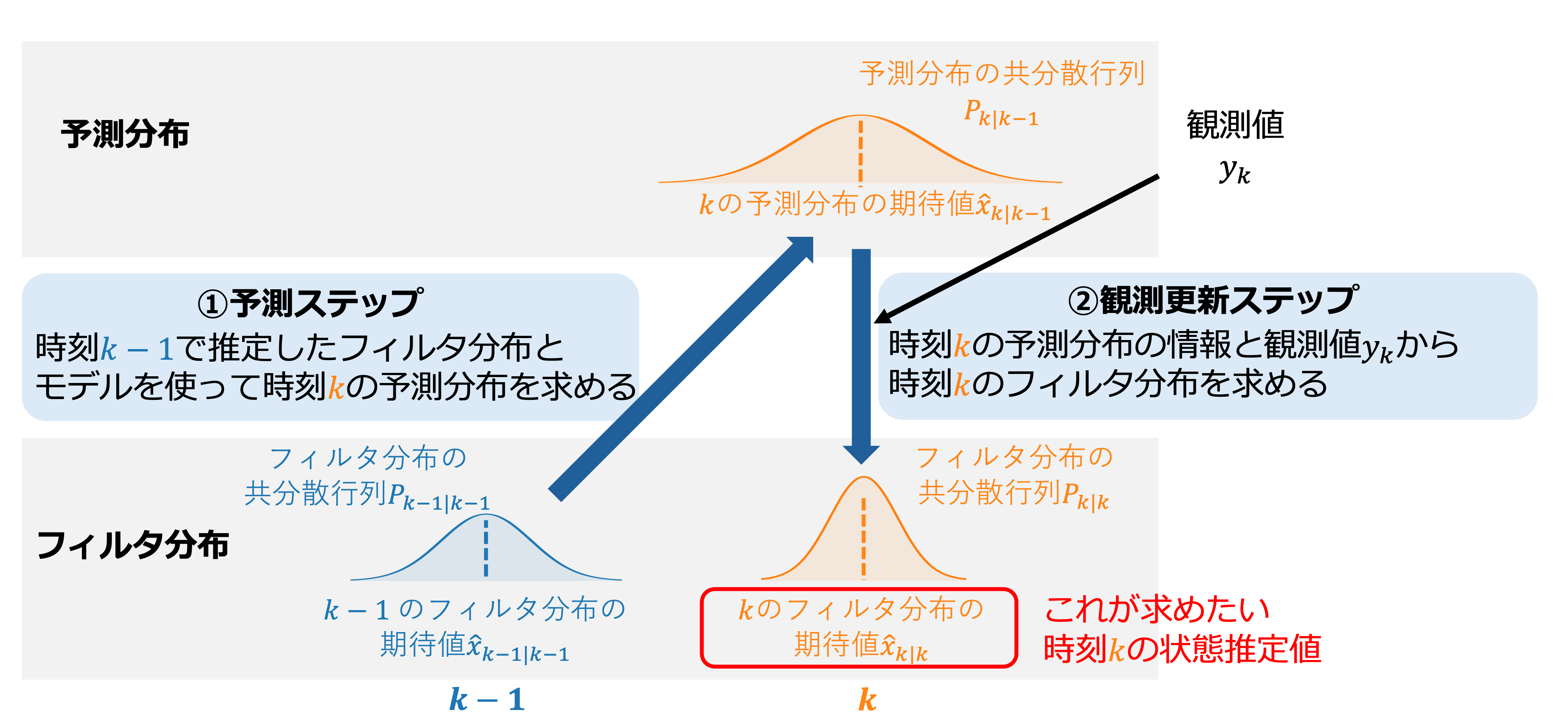
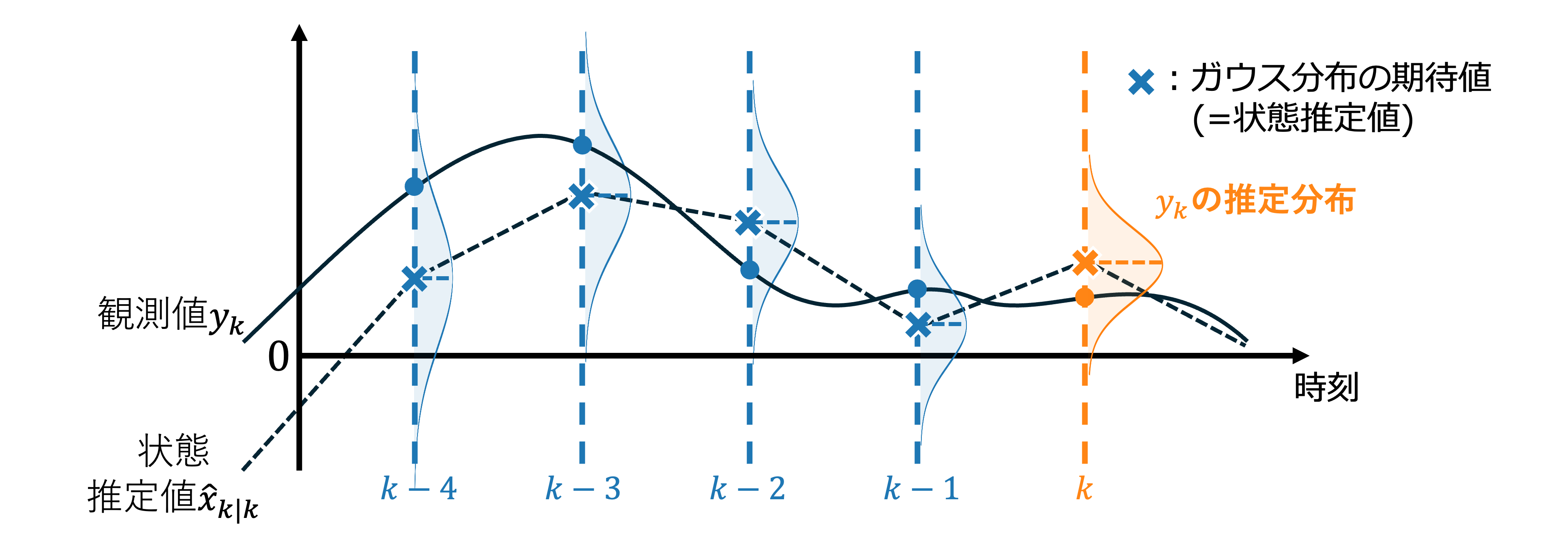
spring_object_damper

以上のように各時刻での\({x}_{𝑘}\)がガウス分布に従っていると仮定して、各時刻で推定したフィルタ分布の期待値である\(\hat{x}_{k|k}\)が最終的に求める状態推定値となります。下の図のように時刻が早い段階では状態\(x_k\)の推定分布(ガウス分布)は裾が広い(分散が大きい)ので観測値\({y}_k\)から乖離している可能性が高いです。しかしステップが進むにつれ観測値\(y_k\)によって分布が更新され状態推定値が観測値\({y}_k\)に近づき、推定分布の分散が小さくなっていくことで状態推定値\(\hat{x}_{k|k}\)の確からしさが向上していきます。このように各時刻で推定したフィルタ分布の期待値が状態推定値\(\hat{x}_{𝑘|k}\)となり、その分散(共分散行列)の値から状態推定値の確からしさがわかります。

spring_object_damper

またこのような線形確率システムのためのカルマンフィルタを線形カルマンフィルタと呼びます。非線形確率システムのためのカルマンフィルタには拡張カルマンフィルタやUnscentedカルマンフィルタ等がありますが、本記事では最も基本的な線形カルマンフィルタについて扱います。

カルマンフィルタの導出#

ここまでに、フィルタリング問題におけるカルマンフィルタでは予測ステップと観測更新ステップを繰り返しながら状態推定値を更新していくことを説明しました。ここではどうしてその様な処理を行うのか？をクリアにするためにカルマンフィルタアルゴリズムの導出の流れについて数式も交えながら説明します。

先ほど説明した通り、雑音の影響で状態ベクトル \( x_s \) と観測ベクトル \( y_k \) は確率変数となります。時刻 \( k \) までの観測データ \( \{y_1, y_2, \cdots y_k \} \) を \( Y_k \) と定義します。また \( Y_k \) が得られた上での状態ベクトル \( x_s \) の条件付き確率分布を \( p(x_s|Y_k) \) と表記します。「カルマンフィルタとは」の節で登場した予測分布とフィルタ分布は、この条件付き確率分布 \( p(x_s|Y_k)\) の、観測データの時刻 \( k \) と状態ベクトルの時刻 \( s \) の関係に応じた名称になります。

\( p(x_s|Y_k)\) の名称
- 予測分布 \((s > k)\)
- フィルタ分布 \((s = k)\)
- 平滑化分布 \((s < k)\)

予測分布とフィルタ分布の間にはある関係式が成り立ち、それがカルマンフィルタで行っている予測ステップと観測更新ステップの具体的な計算の元となるためこの関係式について説明します。

まず \( x_k \) の予測分布 \( p(x_k|Y_{k-1})\) を \( p(x_k, x_{k-1}|Y_{k-1})\) の周辺分布と見なすことで、\( x_{k-1} \) のフィルタ分布 \( p(x_{k-1}|Y_{k-1}) \) との間の関係式が得られます。以下では、カルマンフィルタで対象とする状態空間モデルにおいて一時刻前の状態ベクトル \( x_{k-1} \) が与えられると、雑音の独立性より \(x_k\) は過去の観測データ \( Y_{k-1} = \{y_1, \cdots, y_{k-1} \} \) とは独立になるという性質を利用しています。

予測ステップ

\[\begin{split} \begin{align*} p(x_k|Y_{k-1}) &= \int p(x_k, x_{k-1}| Y_{k-1}) ~dx_{k-1} \\ &= \int p(x_k|x_{k-1}, Y_{k-1}) ~ p(x_{k-1}|Y_{k-1}) ~dx_{k-1} \\ &= \int p(x_k|x_{k-1}) ~ p(x_{k-1}|Y_{k-1}) ~dx_{k-1} \end{align*} \end{split}\]

最後の式の積分内の \(p(x_{k-1}|Y_{k-1})\) は \(x_{k-1}\) のフィルタ分布です。また \(p(x_k|x_{k-1})\) は状態遷移に関する確率分布です。後に説明するカルマンフィルタの予測ステップの計算はこの関係式に基づき導出されます。

次に \(x_k\) のフィルタ分布 \(p(x_k|Y_k)\) にベイズの定理を適用することで、予測分布 \( p(x_k|Y_{k-1}) \) との間の関係式が得られます。以下では、カルマンフィルタで対象とする状態空間モデルにおいて状態ベクトル \(x_{k}\) が与えられると、観測ベクトル \( y_k \) は過去の観測データ \(Y_{k-1}\) とは独立になるという性質を利用しています。

観測更新ステップ

\[\begin{split} \begin{align*} p(x_k|Y_{k}) = p(x_k|y_k, Y_{k-1}) &= \frac{p(y_k | x_k, Y_{k-1}) ~p(x_k | Y_{k-1})} {p(y_k | Y_{k-1})} \\ &= \frac{p(y_k | x_k) ~p(x_k | Y_{k-1})} {p(y_k | Y_{k-1})} \\ & = \frac{p(y_k | x_k) ~p(x_k | Y_{k-1})} {\int p\left(y_k | x_k\right) p\left(x_k | Y_{k-1}\right) dx_k} \end{align*} \end{split}\]

最後の式の \( p(x_{k}|Y_{k-1}) \) は予測ステップの計算結果である予測分布です。また \(p(y_k|x_k)\) は尤度もしくは尤度関数と呼ばれ、観測測方程式から求まります。後に説明するカルマンフィルタの観測更新ステップの計算はこの関係式に基づき導出されます。

\(x_{k-1}\) のフィルタ分布 \( p(x_{k-1}|Y_{k-1})\) を起点に予測ステップと観測更新ステップを交互に適用することを考えます。 \( p(x_k|x_{k-1}) \) と尤度 \( p(y_k|x_k) \) を用いて、次の時刻の状態ベクトル \(x_{k}\) のフィルタ分布 \( p(x_{k}|Y_{k})\) が得られることが分かります。この関係を整理したのが以下の図になります[4]。

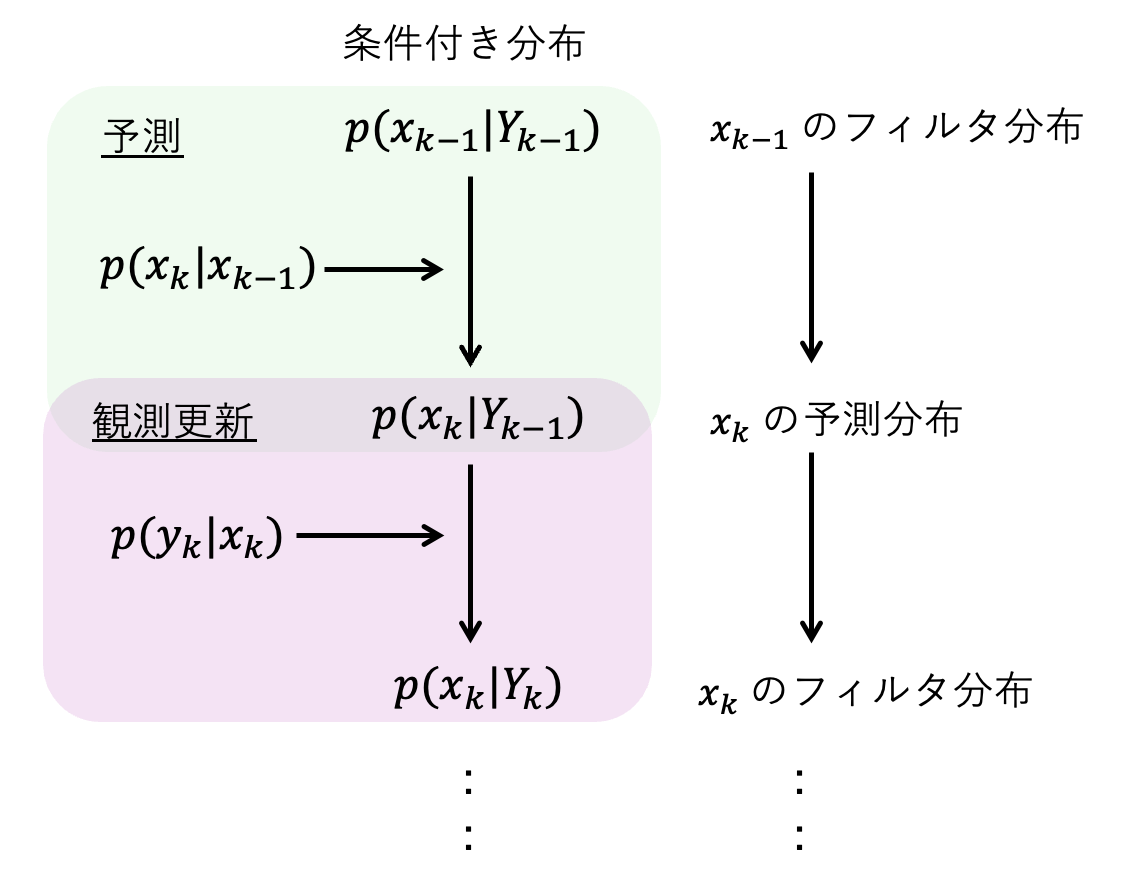
KalmanFilter_update_rule

カルマンフィルタで予測ステップと観測更新ステップを交互に繰り返すのは、そうすることで次の時刻のフィルタ分布が得られるという、条件付き分布の関係式から導かれるこの結果に基づいています。ところが、予測ステップは積分計算であり \( p(x_k|x_{k-1}) \) と \(p(x_{k-1}|Y_{k-1}) \) の形に何らかの仮定をおかないと解析的に解くことは困難です。これはベイズの定理にもとづく観測更新ステップについても同様です。

これに対し、システムの状態空間モデルが線形であること、加わる雑音と状態の初期分布がガウス分布に従うことを含む、カルマンフィルタでおくいくつかの仮定が効いてきます。ここに挙げた2つの仮定を数式で改めて表現すると以下となります。

\[\begin{split} \begin{align*} x_{k+1} &= F_k x_k + G_k w_k, &w_k \sim \mathcal{N}(0, Q_{k}) \\ y_{k} &= H_k x_k + v_k, &v_k \sim \mathcal{N}(0, R_k) \\ x_{0} & \sim \mathcal{N}(\bar{x}_0, P_0) \end{align*} \end{split}\]

また上の仮定は以下を意味します。

\[\begin{split} \begin{align*} p(x_{k}|x_{k-1}) ~&= ~\mathcal{N}(F_{k-1} x_{k-1}, ~G_{k-1}Q_{k-1}G_{k-1}^T) \\ p(y_{k}|x_k) ~&= ~\mathcal{N}(H_{k-1} x_k, ~R_k) \\ p(x_{0}) ~&= ~\mathcal{N}(\bar{x}_0, P_0) \end{align*} \end{split}\]

つまり、予測ステップとフィルタリングステップで利用される状態の遷移確率 \( p(x_k|x_{k-1}) \) と尤度 \( p(y_k|x_k) \)、そして状態の初期分布 \( p(x_0) \) がガウス分布となります。結果、計算される予測分布 \( p(x_k|Y_{k-1}) \) とフィルタ分布 \( p(x_k|Y_k) \) もガウス分布となり解析的に求めることが可能となります。具体的に解を導出すれば予測ステップと観測ステップから成るカルマンフィルタのアルゴリズムが導かれます[2, 3]。導出過程は省略し、以下に結果を記載します。

準備#

以下の状態空間モデルで表されるシステムを対象とします。

\[\begin{split} \begin{align*} % x_{t+1} &= F_{t} x_{t} + D_k u_k + G_k w_k　\\ x_{t+1} &= F_{k} x_{k} + G_k w_k　&状態方程式 \\ y_{k} &= H_{k} x_{k} + v_k　&観測方程式 \\ \end{align*} \end{split}\]

\( x_k \in \mathbb{R}^{n} : \) 状態ベクトル
\( y_k \in \mathbb{R}^{p} : \) 観測ベクトル
\( w_k \in \mathbb{R}^{m} : \) システム雑音
\( v_k \in \mathbb{R}^{p} : \) 観測雑音
\( F_k \in \mathbb{R}^{n \times n} : \) 遷移行列
\( G_k \in \mathbb{R}^{n \times m} : \) 駆動行列
\( H_k \in \mathbb{R}^{p \times n} : \) 観測行列

雑音 \( w_k \) と \( v_k \) は互いに無相関な白色性のガウス雑音であると仮定します。

\[\begin{split} \begin{align*} &w_k \sim \mathcal{N}(0, Q_{k}) \\ &v_k \sim \mathcal{N}(0, R_{k}) \\ &E[w_kw_s^T] = Q_k\delta_{ks} \\ &E[v_kv_s^T] = R_k\delta_{ks} \\ &E[v_kw_s^T] = 0 % &E[v_kw_s^T] = 0, ~~~~t,s=0, 1, \cdots \end{align*} \end{split}\]

状態の初期値 \( x_0 \) はガウス分布に従い、雑音とは無相関であると仮定します。

\[\begin{split} \begin{align*} x_{0} & \sim \mathcal{N}(\bar{x}_0, P_0) \\ &E[w_k x_0^T] = 0 \\ &E[v_k x_0^T] = 0 % &E[v_k x_0^T] = 0, ~~~~t=0, 1, \cdots \end{align*} \end{split}\]

状態空間モデル内の行列 \( F_k, G_k, H_k \) や雑音の共分散行列 \( Q_k, R_k \) には添え字 \( k \) が付いています。これは考えるシステムのダイナミクスや雑音の共分散行列が時間と共に変化しうることを意味します。

カルマンフィルタのアルゴリズム#

初期値の設定

\[ \begin{align*} \hat{x}_{0|0} = \bar{x}_0, ~P_{0|0} = P_0 \end{align*} \]

\( k=1,2 \cdots \) に対して以下を繰り返します。

予測ステップ
- \( (\hat{x}_{k-1|k-1},~ P_{k-1|k-1}) \rightarrow (\hat{x}_{k|k-1},~ P_{k|k-1}) \)
\[\begin{split} \begin{align*} & \hat{x}_{k|k-1} = F_{k-1} \hat{x}_{k-1|k-1}　\\ & P_{k|k-1} = F_{k-1} P_{k-1|k-1} F_{k-1}^T + G_{k-1} Q_{k-1} G_{k-1}^T \end{align*} \end{split}\]
観測更新ステップ
- \( (\hat{x}_{k|k-1},~ P_{k|k-1},~ y_k) \rightarrow (\hat{x}_{k|t},~ P_{k|t}) \)

\[\begin{split} \begin{align*} % & \nu_{t} = y_k - H_k \hat{x}_{k|k-1} \\ & K_k = P_{k|k-1} H_k^T (H_k P_{k|k-1} H_k^T + R_k)^{-1} \\ & \hat{x}_{k|k} = \hat{x}_{k|k-1} + K_k (y_k - H_k \hat{x}_{k|k-1}) \\ & P_{k|k} = P_{k|k-1} - K_k H_k P_{k|k-1} \end{align*} \end{split}\]

アルゴリズム中に記号が多く現れるため一度整理します。

記号
- \( x_k : \) 時刻 \( k \) の状態ベクトル
- \( Y_k : \) 時刻 \( k \) までの観測データ \(\{y_1, \cdots, y_k\} \)
- \( \hat{x}_{s|k} : p(x_{s}| Y_{k}) \) の平均ベクトル
- \( P_{s|k} : p(x_{s}| Y_{k}) \) の共分散行列
- \( F_k : \) 遷移行列
- \( G_k : \) 駆動行列
- \( H_k : \) 観測行列
- \( Q_k : \) 雑音 \( w_k \) の共分散行列
- \( R_k : \) 雑音 \( v_k \) の共分散行列

カルマンフィルタでおく仮定により、予測ステップと観測更新ステップで得られる予測分布とフィルタ分布はガウス分布となることを「カルマンフィルタの導出」の節で説明しました。 \( p(x_s|Y _k) \) の平均ベクトル（期待値ベクトル）と共分散行列を \(\hat{x}_{s|k}, P_{s|k} \) と表記しており、この表記に従うと予測分布とフィルタ分布は以下となります。

\( x _k \) の予測分布
\( p(x_{k} | Y_{k-1}) = \mathcal{N}(\hat{x}_{k|k-1}, P_{k|k-1}) \)
\( x _k \) のフィルタ分布
\( p(x_{k} | Y_{k}) = \mathcal{N}(\hat{x}_{k|k}, P_{k|k}) \)

各ステップの出力より、平均ベクトル（期待値ベクトル）と共分散行列を更新することでそれぞれの分布を更新していることが分かります。
またフィルタ分布の平均ベクトルは時刻 \(k\) における真の状態との平均二乗誤差を最小化する推定値となります。

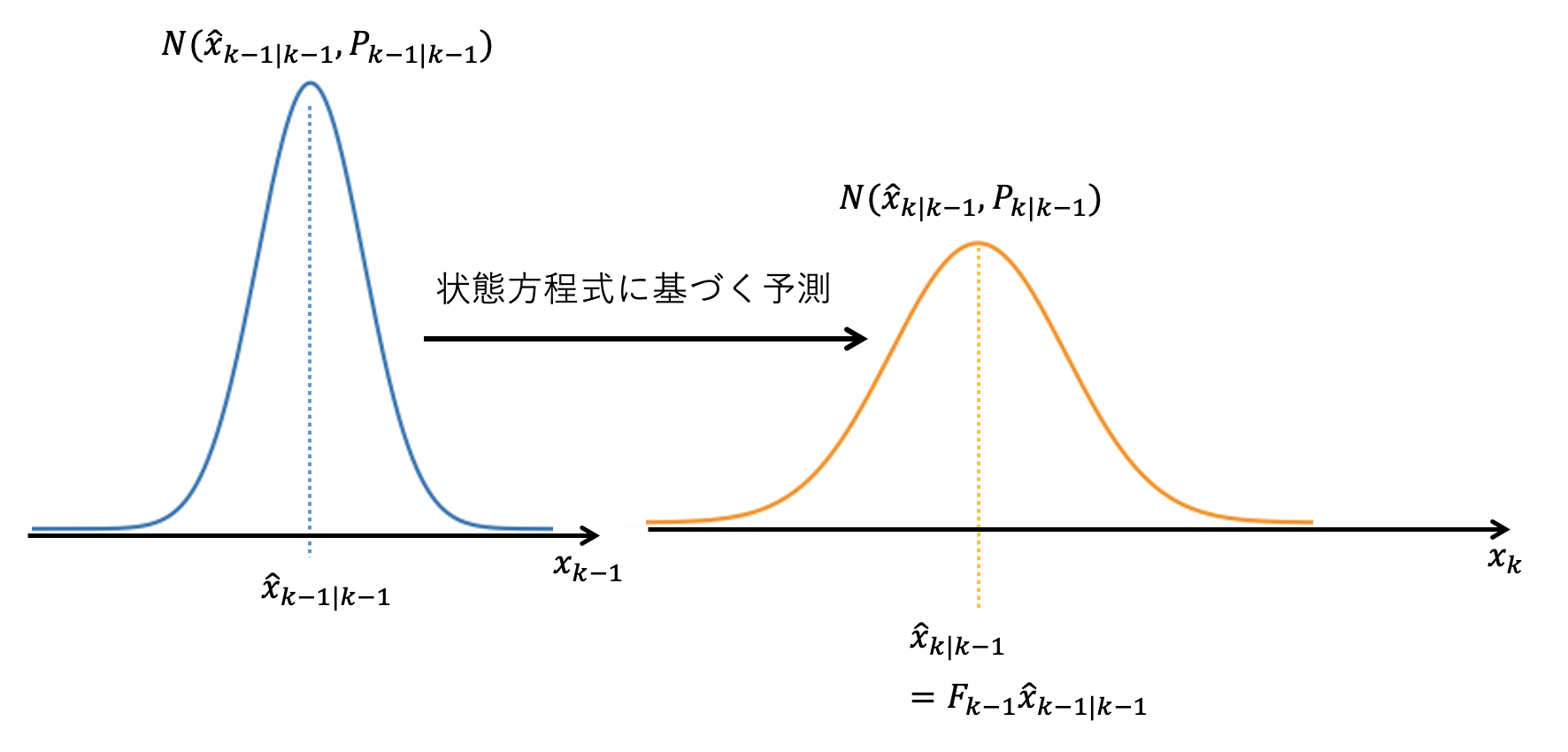
アルゴリズムの中身を見ていきます。予測ステップを見ると、予測分布の平均ベクトル \( \hat{x}_{k|k-1} \) はフィルタ分布の平均ベクトル \( \hat{x}_{k-1|k-1} \) を状態方程式中の行列 \( F_{k-1} \) で遷移させた式になっています。

\[ \begin{align*} \hat{x}_{k|k-1} = F_{k-1} \hat{x}_{k-1|k-1} \end{align*} \]

状態方程式が \( x_k = F_{k-1} x_{k-1} + G_{k-1} w_{k-1} \) であり、雑音 \( w_k \) の平均ベクトルが \( 0 \) であることを考えると、これは状態方程式を利用して \( \hat{x}_{k-1|k-1} \) から \( \hat{x}_{k|k-1} \) を予測していると見ることができます。時刻 \(k-1\) のフィルタ分布から時刻 \(k\) の予測分布へ更新される様子を下図に表します。

KalmanFilter_distribution_predict

次に観測更新ステップを見ます。フィルタ分布の平均ベクトルの更新式は以下となっています。

\[\begin{split} \begin{align*} \hat{x}_{k|k} = \hat{x}_{k|k-1} + K_k (y_k - H_k \hat{x}_{k|k-1}) \\ \end{align*} \end{split}\]

観測方程式より \( H_k \hat{x}_{k|k-1} \) は \( y_k \) の予測値と見なせるため、上の式では予測分布の平均ベクトル \( \hat{x}_{k-1|k} \) を観測ベクトルとその予測値の差に基づき修正していることが分かります。 \( K _k \) はカルマンゲインと呼ばれます。
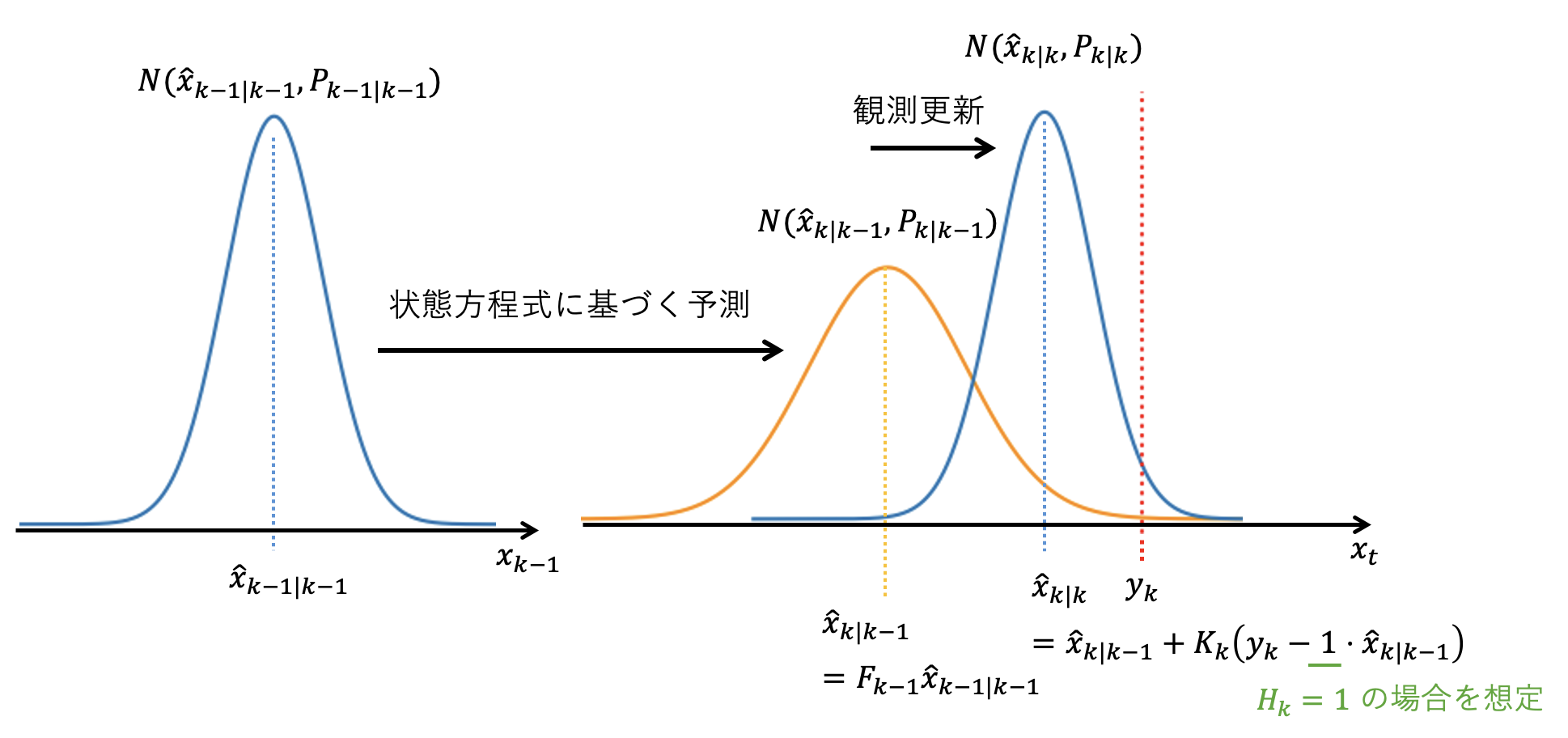
観測更新により \( x_k \) の予測分布が修正されフィルタ分布が求まる様子を下の図に示します。観測値 \( y_k \) を赤の破線で表示しています。またイメージし易くなるよう \( H_k = 1 \) とおき、\( x_k \) と \( y_k \) は同じ次元上にある場合を想定します。

KalmanFilter_distribution_update

カルマンフィルタを使うにあたり、値の設定が必要となる変数を改めて整理します。

状態空間モデル中の行列 \(F_k, G_k, H_k\)
フィルタ分布の初期値 \( \hat{x}_{0|0}, P_{0|0} \)
雑音の共分散行列 \( Q_k, R_k \)

まず「状態空間モデルの」節でも説明した様に、カルマンフィルタはモデルにもとづく手法であるため、事前に対象とするシステムの状態空間モデルを構築し、モデル内の \( F_k, G_k, H_k \) がパラメータを含む場合はその値を推定しておく必要があります。モデルは状態推定値の精度に影響するためこれは重要な話題ですが、ここでは説明しません。興味のある方は制御工学のシステム同定の文献や[6]、モデリングについて言及した時系列解析の文献などをご覧下さい。

他には、フィルタ分布の初期値 \( \hat{x}_{0|0}, P_{0|0} \) と雑音の共分散行列 \( Q_k, R_k \) があります。これらは調整パラメータになります。文献[1]では、\( \hat{x}_{0|0} \) は利用できる情報がある場合はそれを利用して初期化し、ない場合は \( \hat{x}_{0|0} = 0 \) として初期することが多い。また \( P_{0|0} = \alpha I \) として初期化することが多いと述べています。

例題#

簡単な例題を解いて理解を深めましょう。ローカルレベルモデルと呼ばれる、ランダムウォークにノイズが加わったモデルにカルマンフィルタを適用してみます。

ローカルレベルモデル（ランダムウォーク + ノイズモデル）

\[\begin{split} \begin{align*} x_{t+1} = x_k + w_k \\ y_k = x_k + v_k \end{align*} \end{split}\]

カルマンフィルタについてはfilterpyというpythonパッケージの実装を利用します。

import numpy as np
import matplotlib.pyplot as plt
from filterpy.kalman import KalmanFilter

np.random.seed(1)

カルマンフィルタオブジェクトを作成し、カルマンフィルタが対象とするシステムのパラメータを設定します。具体的には、状態空間モデルの行列と雑音の共分散行列の値を設定します。
今回は状態空間モデルの行列が \( F_k, = 1,~ G_k=1, ~H_k=1 \) の場合のモデルになります。また雑音 \( w_k \) と \( v_k \) の共分散行列は \( Q_k = 1,~ R_k = 4 \) とし、これらの値は既知であると仮定します。

kf = KalmanFilter(dim_x=1, dim_z=1)

kf.F = np.array([[1]])  # 遷移行列
kf.H = np.array([[1]])  # 観測行列

covar_w = 1
covar_v = 4
kf.Q = np.array([[covar_w]])  # システムノイズの共分散行列
kf.R = np.array([[covar_v]])  # 観測ノイズの共分散行列

なお、filterpyのKalmanFilterクラスではシステムの状態空間モデルが常に \( G_k = I \) （単位行列）であることを想定しているようです。ローカルレベルモデルは \( G_k = 1 \) であるため気にする必要はありませんが、以下のように机上で検討しているモデルとその実装とでシステム雑音 \( w_k \) の項に差異がある場合は、それを考慮して共分散行列を設定する必要があります。

検討している状態空間モデル
\(x_{t+1} = F_k x_k + G_k w_k \)
KalmanFilterクラスが想定している状態空間モデル
\(x_{t+1} = F_k x_k + w_k' \)

\( w_k,~ w_k'\) の共分散行列をそれぞれ \( Q_k, Q_k' \) とします。 \( w_k \) の共分散行列をある値 \( Q_k \) として設定することを考えます。これをクラス側が想定している \( Q_k' \) へ変換するには以下より

\[ \begin{align*} Q_k' &= E[w_k' {w_k'}^T] = E[(G_k w_k)(G_k w_k)^T] = G_k E[w_k {w_k}^T] {G_k}^T = G_k Q_k {G_k}^T \end{align*} \]

\( Q_k \) の左右から \( G_k \) と \( {G_k}^T\) を乗じる必要があります。この値をクラス側へ設定しましょう。

例題に戻ります。ローカルレベルモデルにもとづく時系列データは予め生成しておくことにします。状態の初期値は適当に \( 5 \) としました。

steps = 150

xs = np.zeros(steps)
ys = np.zeros(steps)
xs[0] = 5  # 状態の初期値

for k in range(steps):

    # ガウスノイズ
    w = np.random.normal(loc=0, scale=np.sqrt(covar_w))
    v = np.random.normal(loc=0, scale=np.sqrt(covar_v))

    # ローカルレベルモデル
    if (k + 1) < steps:
        # 状態方程式（ランダムウォーク）
        xs[k + 1] = xs[k] + w
    # 観測方程式
    ys[k] = xs[k] + v

カルマンフィルタによる状態推定では予測分布とフィルタ分布の更新を繰り返すので、それぞれの結果を格納する変数を用意します。

x_pred_means = np.zeros(steps)
x_pred_covars = np.zeros(steps)

x_filt_means = np.zeros(steps)
x_filt_covars = np.zeros(steps)

ここからがカルマンフィルタのアルゴリズム部分になります。まずはフィルタ分布の初期値 \( \hat{x}_{0|0} \) と \( P_{0|0} \) を設定します。ここでは \( y_0 \) が観測できるとし \( \hat{x}_{0|0} = y_0 \) としました。雑音の影響はあるものの、観測値から遠くない位置に状態は在るだろうという仮説です。また \( P_{0|0} = 10 \) としました。

kf.x[0, 0] = ys[0]
kf.P[0, 0] = 10
x_filt_means[0], x_filt_covars[0] = kf.x[0, 0], kf.P[0, 0]

それではカルマンフィルタによる状態推定を行なっていきます。 \( k = 1, 2 \cdots \) において予測ステップと観測更新ステップを繰り返します。
時刻の状態推定において利用するのは時刻 \( k \) の観測値 \( y_k \) のみとなります。

for k in range(1, steps):

    # カルマンフィルタによる状態推定
    # 予測ステップ
    kf.predict()
    x_pred_means[k], x_pred_covars[k] = kf.x_prior[0, 0], kf.P_prior[0, 0]

    # 観測更新ステップ
    kf.update(ys[k])  # 同時刻の観測値y[t]のみを使用
    x_filt_means[k], x_filt_covars[k] = kf.x_post[0, 0], kf.P_post[0, 0]

結果を可視化します。観測値 \( y_k \)、真の状態 \(x_k\) カルマンフィルタによる状態推定値 \(\hat{x}_{k|k}\) （フィルタ分布の平均値）を並べてみます。

fig, ax = plt.subplots(figsize=(8, 5))

ax.plot(np.arange(steps), ys, "x:", markersize=4, alpha=0.8, color="orchid")
ax.plot(np.arange(steps), xs, "o:", markersize=3.5, alpha=0.6, color="limegreen")
ax.plot(
    np.arange(steps), x_filt_means, "o-", markersize=3.5, alpha=0.6, color="dodgerblue"
)

ax.legend(["y(k)", "x(k)", "x^(k|k)"])
ax.set_xlabel("time")
ax.grid(True)

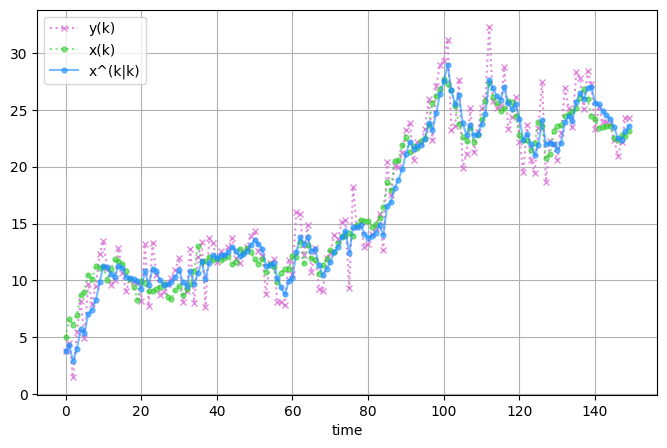
../_images/fbba8525cacabbee9c20993284f1ed5d081f3a56ec873b0f8c0720dbae0802e3.png

状態 \( x_k \) はガウス雑音 \( w_k \) により次の状態 \(x_{k+1}\) に遷移します。さらにガウス雑音 \( v_k \) が加わったものが \( y_k \) となります。雑音により \(x_k, ~y_k\) がランダムに振る舞う様子が見て取れます。またばらつきは \( y_k \) が最も大きそうです。これは \( y_k = x_k + v_k = x_{k-1} + w_{k-1} + v_k \) となり \( y_k \) には2つのガウス雑音が加わることから理解できます。カルマンフィルタによる状態推定値 \( \hat{x}_{k|k} \) を見ると、雑音にまみれた \(y_k\) から概ね \(x_k\) に近い値を推定できていそうです。

少し見方を変えましょう。以下の図は縦軸を時間軸とし、観測値 \( y_k \) 、カルマンフィルタの予測分布の平均 \( \hat{x}_{k|k-1} \)、フィルタ分布の平均 \( \hat{x}_{k|k} \) をプロットしたものです。

fig, ax = plt.subplots(figsize=(7, 5))

short_steps = 20
ax.plot(
    ys[:short_steps],
    np.arange(short_steps),
    "x:",
    markersize=4,
    alpha=0.8,
    color="orchid",
)

ax.plot(
    x_pred_means[1:short_steps],
    np.arange(1, short_steps),
    "o-",
    markersize=4,
    alpha=0.6,
    color="darkorange",
)

ax.plot(
    x_filt_means[:short_steps],
    np.arange(short_steps),
    "o-",
    markersize=4,
    alpha=0.6,
    color="dodgerblue",
)

ax.legend(["y(k)", "x^(k|k-1)", "x^(k|k)"])
ax.set_ylabel("time")
ax.set_xlabel("x(k), y(k)")
ax.set_yticks(np.arange(0, short_steps + 1, 2))
ax.set_xlim([min(ys[:short_steps]) - 5, max(ys[:short_steps]) + 5])

ax.grid(True)

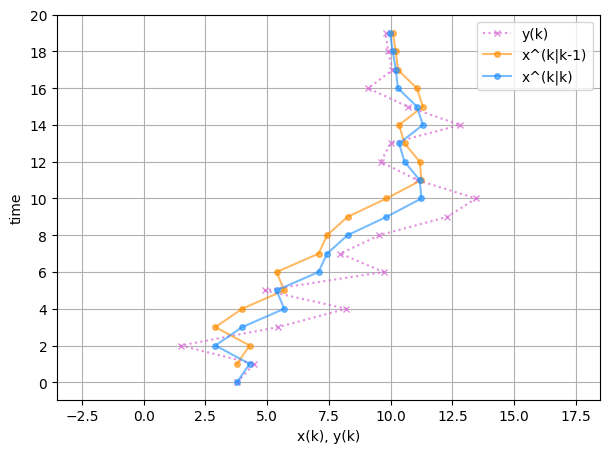
../_images/5ca5538543e00048d81e9a539883788780bd3709c6f7349d0b74f1748e71c0f5.png

\( \hat{x}_{k|k} \) が \( \hat{x}_{k|k-1} \) と観測値 \( y_k \) の間に位置することが分かります。これはアルゴリズムが「予測分布の平均 \( \hat{x}_{k|k-1} \) の計算 → 観測値 \( y_k \) の取得 → \( y_k \) を用いたフィルタ分布の平均 \( \hat{x}_{k|k} \) の計算（補正）」という手順を踏むためです。

さらに、予測分布とフィルタ分布が時刻と共にどのように変化していくのか見てみましょう。まずは \( k=0 \) における初期のフィルタ分布 \( p(x_0|Y_0) \) と観測値 \( y_0 \) を可視化してみます。

def gaussian(x, mu, covar):
    c = 1 / np.sqrt(2 * np.pi * covar)
    y = c * np.exp(-((x - mu) ** 2) / (2 * covar))
    return y


k = 0

lhs = min(ys) - 30
rhs = max(ys) + 30
x_range = np.arange(lhs, rhs, (rhs - lhs) / 1e3)

fig, ax = plt.subplots(figsize=(7, 4))
ax.set_title(f"k={k}")
ax.axvline(ys[k], linestyle=":", linewidth=2, color="orchid")

prob = gaussian(x_range, x_filt_means[k], x_filt_covars[k])
ax.plot(x_range, prob, color="dodgerblue")
ax.legend([f"y({k})", f"p(x({k})|Y({k}))"])
ax.set_xlim(min(ys[:short_steps]) - 10, max(ys[:short_steps]) + 10)
ax.set_ylim([-0.05, 0.35])
ax.grid(True)

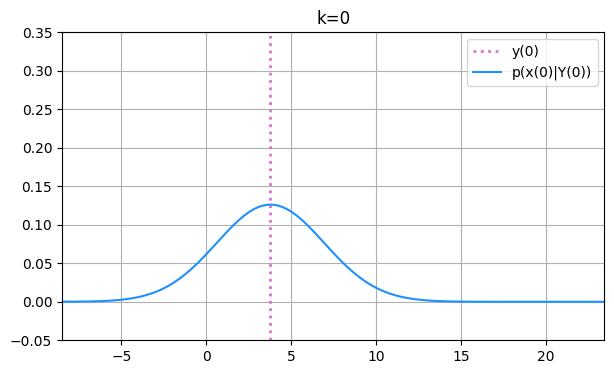
../_images/826beb18aed9aa97a2dccefb2584d98b098c955d18eff04487639ffd98647e5b.png

カルマンフィルタ初期化時に、最初のフィルタ分布 \( p(x_0|Y_0) \) の平均を観測値 \( y_0 \) に、分散を \( 10 \) に設定しました。その通りの分布が描かれています。続いて初期化後のカルマンフィルタ実行による確率分布の変化を見ていきます。ここからは予測分布も合わせてプロットします。

fig, axes = plt.subplots(3, 1, figsize=(7, 10))

for k, ax in zip([1, 2, 3], axes):

    ax.set_title(f"k={k}")

    ax.axvline(ys[k], linestyle=":", linewidth=2, color="orchid")

    prob = gaussian(x_range, x_pred_means[k], x_pred_covars[k])
    ax.plot(x_range, prob, color="darkorange")

    prob = gaussian(x_range, x_filt_means[k], x_filt_covars[k])
    ax.plot(x_range, prob, color="dodgerblue")

    ax.legend([f"y({k})", f"p(x({k})|Y({k-1}))", f"p(x({k})|Y({k}))"])
    ax.set_xlim(min(ys[:short_steps]) - 5, max(ys[:short_steps]) + 5)
    ax.set_ylim([-0.05, 0.35])
    ax.grid(True)

fig.tight_layout()

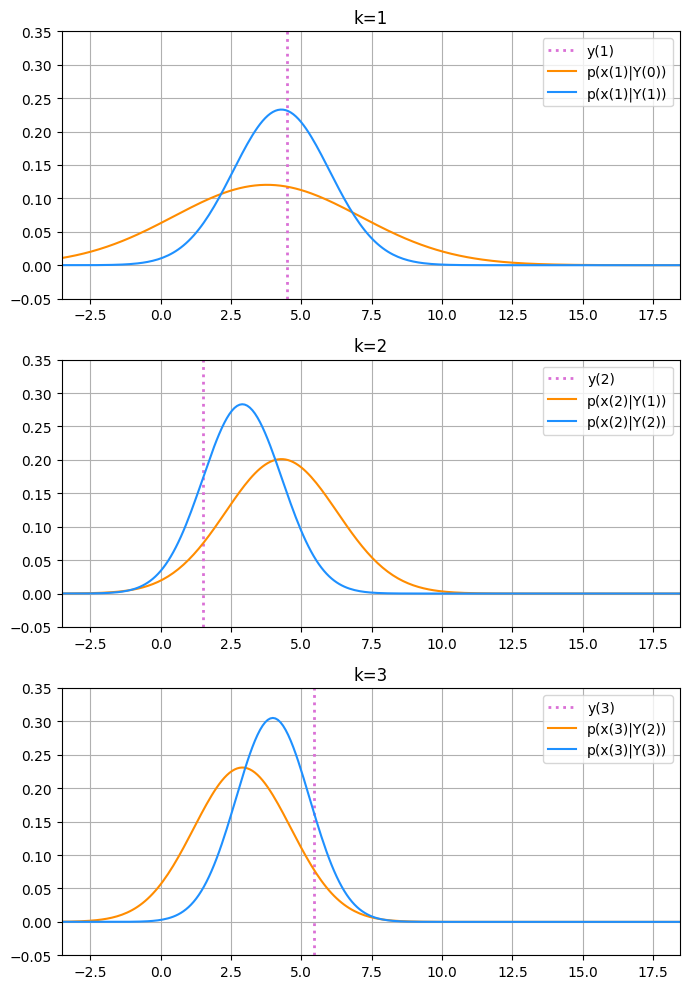
../_images/5c8bb5588821fbbf8f5104a94b83eece073813d39e004558ff8585d683e0b7f1.png

予測分布の更新と、観測値により予測分布が補正されフィルタ分布が求まる様子がよく分かると思います。ここで、予測ステップと更新ステップによる分布の分散の変化に注目します。

予測ステップ
\( k-1 \) のフィルタ分布（青線） → \( k \) の予測分布（橙線）への更新
観測更新ステップ
\( k \) の予測分布（橙線） → \( k \) のフィルタ分布（青線）への更新

例えば \(k=2, ~3\) のそれぞれのプロットを見ると、予測ステップでは（ \(k=2\) の青線 \(\rightarrow\) \( k=3 \) の橙線）更新前よりも分布の分散は少し大きくなり、観測更新ステップでは（ \(k=3\) の橙線 \(\rightarrow\) \( k=3 \) の青線）更新前よりも分布の分散が小さくなっていることが分かるでしょうか。これはローカルレベルモデルにカルマンフィルタを適用した場合の共分散行列の式から理解できます。カルマンフィルタのアルゴリズムに今回の状態空間モデルのパラメータを代入すると以下が得られます。

予測ステップ

\[ \begin{align*} P_{k|k-1} = P_{k-1|k-1} + Q \end{align*} \]

予測ステップにより、\( t \) の予測分布の分散 \( P_{k|k-1} \) は\( k-1 \) のフィルタ分布の分散 \( P_{k-1|k-1} \) よりも必ず大きくなることが分かります。

観測更新ステップ

\[\begin{split} \begin{align*} K_k &= \frac{P_{k|k-1}}{(P_{k|k-1} + R)} \\ P_{k|k} &= P_{k|k-1} - K_k P_{k|k-1} \end{align*} \end{split}\]

\( K_k > 0 \) となるため、観測更新ステップにより \( k \) のフィルタ分布の分散 \( P_{k|k} \) は \( k \) の予測分布の分散 \( P_{k|k-1} \) よりも必ず小さくなることが分かります。分散を推定値に対する自信のようなものだと捉えると、観測更新ステップでは観測値を用いることで推定値に対する自信が増していると解釈できるかもしれません。

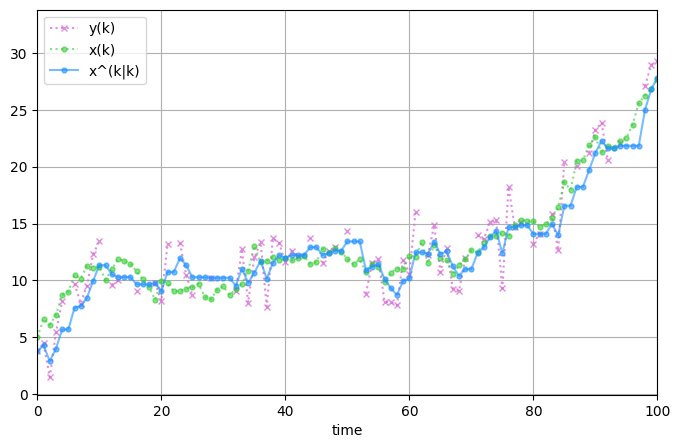
欠損値がある場合の処理#

最後に欠損値がある場合の処理について少し説明します。何らかの理由によりある時刻や区間において観測値が観測できない場合、観測更新ステップが行えないためその時刻では予測ステップのみを行うことになります。そして観測更新ステップは観測値が得られた段階で行います。これは観測値が得られない区間において、1つ先だけでなくさらに先の状態を含めた長期の予測問題を解いていることになります。欠損値がある場合を想定したfiliterpyを用いたコードを以下に示します。

# 再初期化
kf.x[0, 0] = ys[0]
kf.P[0, 0] = 10
x_filt_means[0], x_filt_covars[0] = kf.x[0, 0], kf.P[0, 0]

# 観測値が得られない時刻をセット
not_observed_kimes = np.random.choice(steps, 50)
ys_sub = ys.copy()
ys_sub[not_observed_kimes] = np.nan

for k in range(1, steps):

    # 欠損値を含む場合のカルマンフィルタによる状態推定
    # 予測ステップ
    kf.predict()
    x_pred_means[k], x_pred_covars[k] = kf.x_prior[0, 0], kf.P_prior[0, 0]

    if not np.isnan(ys_sub[k]):
        # 観測値y[t]が得られた場合のみ観測更新ステップを行う
        kf.update(ys_sub[k])
    x_filt_means[k], x_filt_covars[k] = kf.x_post[0, 0], kf.P_post[0, 0]

fig, ax = plt.subplots(figsize=(8, 5))
ax.plot(np.arange(steps), ys_sub, "x:", markersize=4, alpha=0.8, color="orchid")
ax.plot(np.arange(steps), xs, "o:", markersize=3.5, alpha=0.6, color="limegreen")
ax.plot(
    np.arange(steps), x_filt_means, "o-", markersize=3.5, alpha=0.6, color="dodgerblue"
)
ax.set_xlim([0, 100])

ax.legend(["y(k)", "x(k)", "x^(k|k)"])
ax.set_xlabel("time")
ax.grid(True)

../_images/138fd5cae001ebbdc7b86c67b4c74e8eb2ea1032c99b371ec410ec6508973f7c.png

小括#

本稿では状態推定の代表的な手法であるカルマンフィルタについて解説しました。具体的には、アルゴリズムの概要、アルゴリズムの各処理で行っていること、そしてその背景等について図や数式を交えて解説し、簡単な例題とソースコードを通して理解が深まるようにしました。またカルマンフィルタを解説する上で欠かすことができない状態空間モデルと状態推定問題についても簡単に解説しました。

参考文献#

足立修一, 丸田一郎 : カルマンフィルタの基礎, 東京電機大学出版局.
片山徹 : 非線形カルマンフィルタ, 朝倉書店.
樋口知之, 上野玄太, 中野慎也, 中村和幸, 吉田亮 : データ同化入門, 朝倉書店.
浅野太 : 音のアレイ信号処理, コロナ社.
Y. Bar-Shalom, X. Rong Li, and T. Kirubarajan : Estimation with applications to tracking and navigation, John Wiley and Sons.
足立修一 : システム同定の基礎, 東京電機大学出版局.
佐藤和也, 下本陽一, 熊澤典良 : はじめての現代制御理論, 講談社サイエンティフィク.
Chachay, 連続時間システムの離散化手法の比較 [Python Scipy]", ヤカンヒコウ, 2021-05-15, (参照2025-01-08).
大住晃, 亀山建太郎, 松田吉隆 : カルマンフィルタとシステムの同定動的逆問題へのアプローチ, 森北出版.

カルマンフィルタ

目次

カルマンフィルタ#

はじめに#

状態空間モデルと状態推定問題#

状態空間モデルとは#

状態推定問題#

カルマンフィルタとは#

カルマンフィルタの導出#

準備#

カルマンフィルタのアルゴリズム#

例題#

欠損値がある場合の処理#

小括#

参考文献#