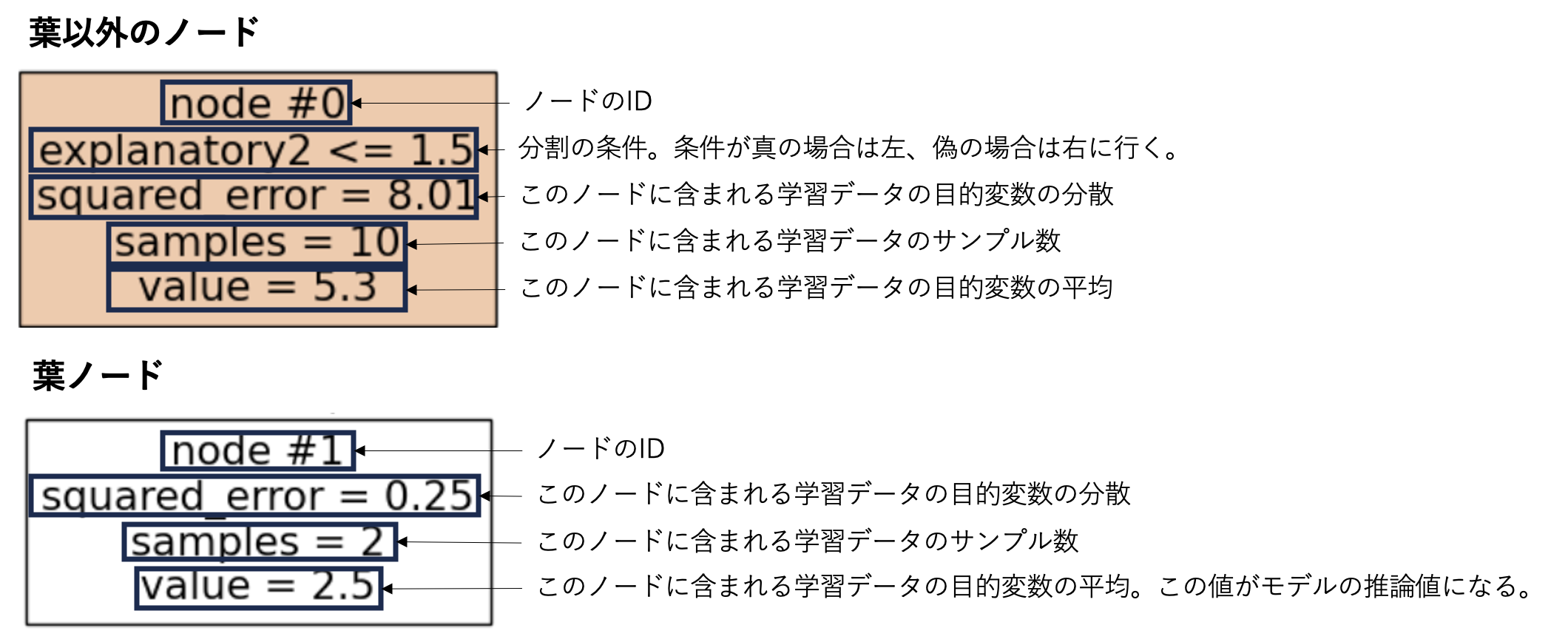
決定木回帰モデル#
このページでは決定木回帰モデルについて解説します。
決定木回帰モデルは木(tree)と呼ばれるデータ構造を用いた機械学習モデルで、以下のような特徴を持っています。
非線形モデルである
特徴量重要度を算出できる
比較的少ない前処理で実行できる
後述する分割の条件等はハイパーパラメータによって変化しますが、本稿ではsklearn.tree.DecisionTreeRegressorのデフォルトの実装に従って解説をします。
木構造と決定木回帰モデルの概要#
木(有向木)とは、以下のような閉路を持たない連結な有向グラフの事を指します。

根から順番に枝分かれをしていき、末端のノードを葉と呼びます。
各エッジに対して、エッジの根本を親ノード、行き先を子ノードと呼びます。
(特に上画像のような各ノードが高々2個の子ノードしか持たない有向木を二分木と呼びます。)
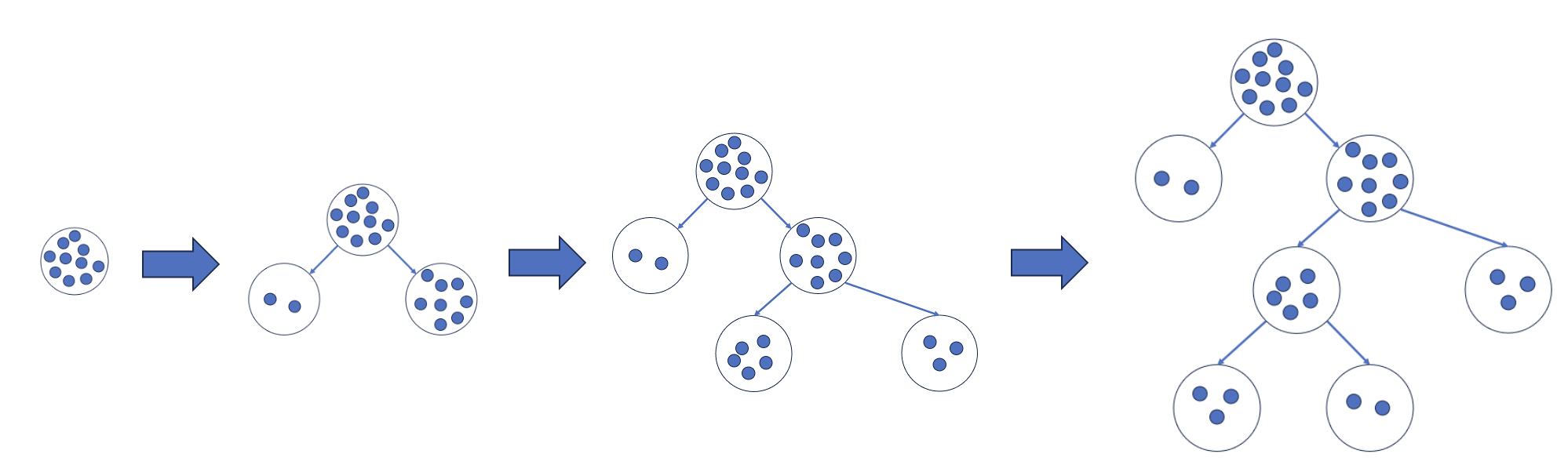
木を機械学習に応用する場合は以下のように学習データの分割をします。
分割は説明変数に対する条件の真偽で行い、分割を繰り返す事で木が作成されます。
分割が終わった後、それぞれの葉に対応する推論値を算出します。

推論時には、入力されたサンプルがどの葉に入るかを各条件に従って計算し、入力されたサンプルが入った葉の推論値をモデルの推論値として返します。
決定木の可視化#
アルゴリズムの詳細な説明に移る前に、まずは学習済み決定木回帰モデルの可視化をしてみます。
今回は以下のデータを使って学習をします。
import pandas as pd
df = pd.DataFrame({'explanatory1': (0, 1, 2, 3, 4, 5, 6, 7, 8, 9),
'explanatory2': (3, 6, 5, 4, 7, 0, 10, 1, 2, 5),
'objective': (5, 1, 5, 10, 4, 2, 9, 3, 8, 6)})
df
| explanatory1 | explanatory2 | objective | |
|---|---|---|---|
| 0 | 0 | 3 | 5 |
| 1 | 1 | 6 | 1 |
| 2 | 2 | 5 | 5 |
| 3 | 3 | 4 | 10 |
| 4 | 4 | 7 | 4 |
| 5 | 5 | 0 | 2 |
| 6 | 6 | 10 | 9 |
| 7 | 7 | 1 | 3 |
| 8 | 8 | 2 | 8 |
| 9 | 9 | 5 | 6 |
explanatory1とexplanatory2が説明変数で、objectiveが目的変数です。
デフォルト設定のまま学習をすると全ての葉に含まれるサンプル数が 1 になってしまうので、説明をしやすくするため各ノードのサンプル数が 2 以上になるオプションをつけて学習します。
from sklearn.tree import DecisionTreeRegressor
# 学習
regressor = DecisionTreeRegressor(min_samples_leaf=2)
regressor.fit(df.loc[:,["explanatory1", "explanatory2"]].values, df["objective"].values)
DecisionTreeRegressor(min_samples_leaf=2)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
DecisionTreeRegressor(min_samples_leaf=2)
scikit-learnにはplot_treeという便利な関数が用意されており、学習済みの決定木を可視化できます。
import matplotlib.pyplot as plt
from sklearn.tree import plot_tree
# 可視化
plt.figure(figsize=(10, 10))
plot_tree(regressor, feature_names=df.columns, node_ids=True, filled=True)
plt.show()

上記の画像に含まれている情報から、このモデルがどのような推論結果を返すのか、各説明変数の特徴量重要度がどうなるか、を全て読み取る事ができます。
まず各ノードに書いてある式を説明します。
このplot_treeの出力画像を使って、推論アルゴリズム、特徴量重要度算出アルゴリズム、学習アルゴリズムの順番で解説していきます。
推論アルゴリズム#
推論時には、入力されたサンプルがどの葉に入るかを各ノードの分割の条件に従って計算し、入力されたサンプルが入った葉の推論値をモデルの推論値として返します。
実際に以下のサンプルの推論が上記の学習済みモデルでどのように行われるか観察してみます。
df_sample1 = pd.DataFrame({'explanatory1': (2,), 'explanatory2': (1,)})
df_sample1
| explanatory1 | explanatory2 | |
|---|---|---|
| 0 | 2 | 1 |
推論の流れは以下のようになります。

node #0 では「explanatory2 ≤ 1.5」が条件になっており、条件を満たしているため左の node #1 に移ります。
node #1 は葉なので対応する予測値(2.5)を返します。
実際に以下のコードで予測値を確認すると 2.5 になっています。
regressor.predict(df_sample1.values)
array([2.5])
もう1回、値を変えて観察してみます。
df_sample2 = pd.DataFrame({'explanatory1': (3,), 'explanatory2': (2,)})
df_sample2
| explanatory1 | explanatory2 | |
|---|---|---|
| 0 | 3 | 2 |
この場合の推論の流れは以下のようになります。
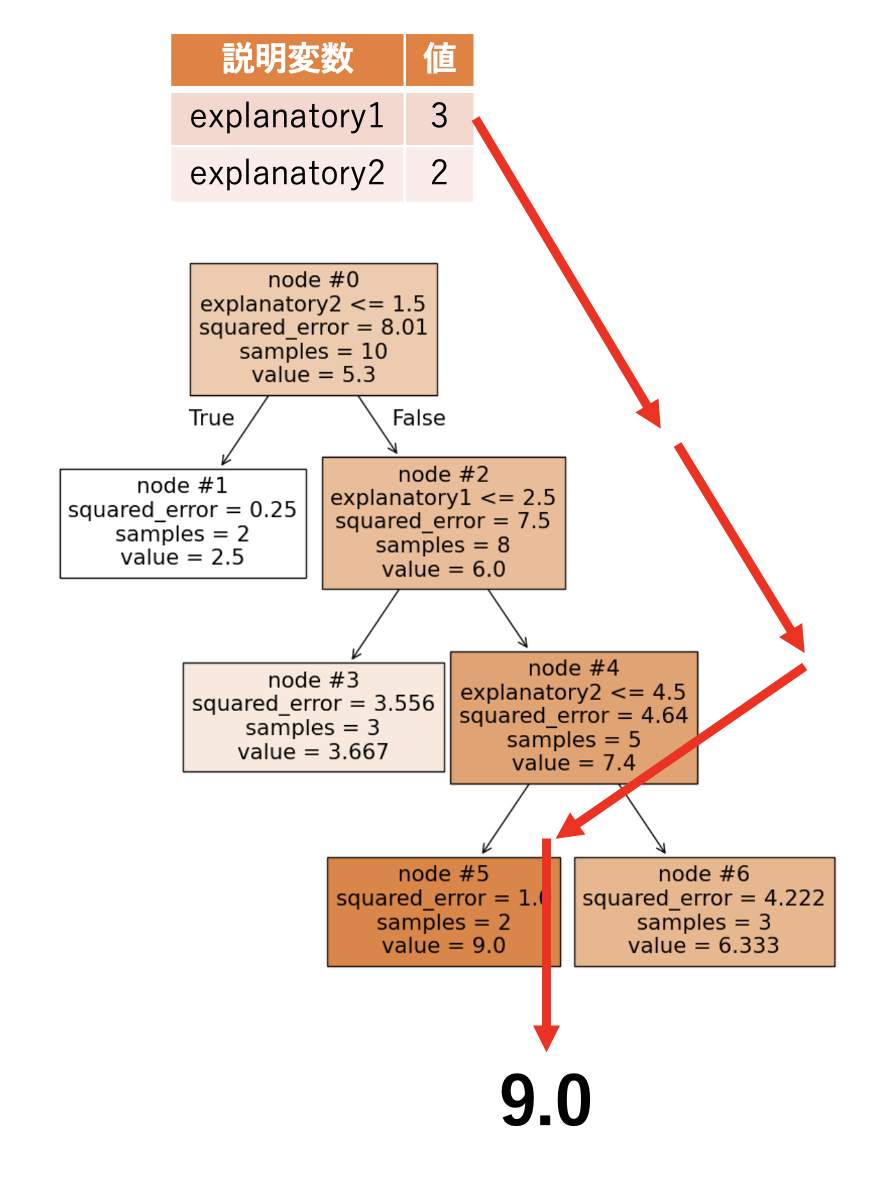
node #0 では「explanatory2 ≤ 1.5」が条件になっており、条件を満たしていないため右の node #2 に移ります。
node #2 では「explanatory1 ≤ 2.5」が条件になっており、条件を満たしていないため右の node #4 に移ります。
node #4 では「explanatory2 ≤ 4.5」が条件になっており、条件を満たしているため左の node #5 に移ります。
node #5 は葉なので対応する予測値(9.0)を返します。
実際に以下のコードで予測値を確認すると 9.0 になっています。
regressor.predict(df_sample2.values)
array([9.])
特徴量重要度算出アルゴリズム#
ある説明変数の特徴量重要度 (impurity-based feature importances) は、その説明変数を分割の条件に使っているノードごとに計算された値の和を正規化する事で得られます。
図で表すと以下のようになります。(「ノードごとに計算された値」については図の後に説明します。)
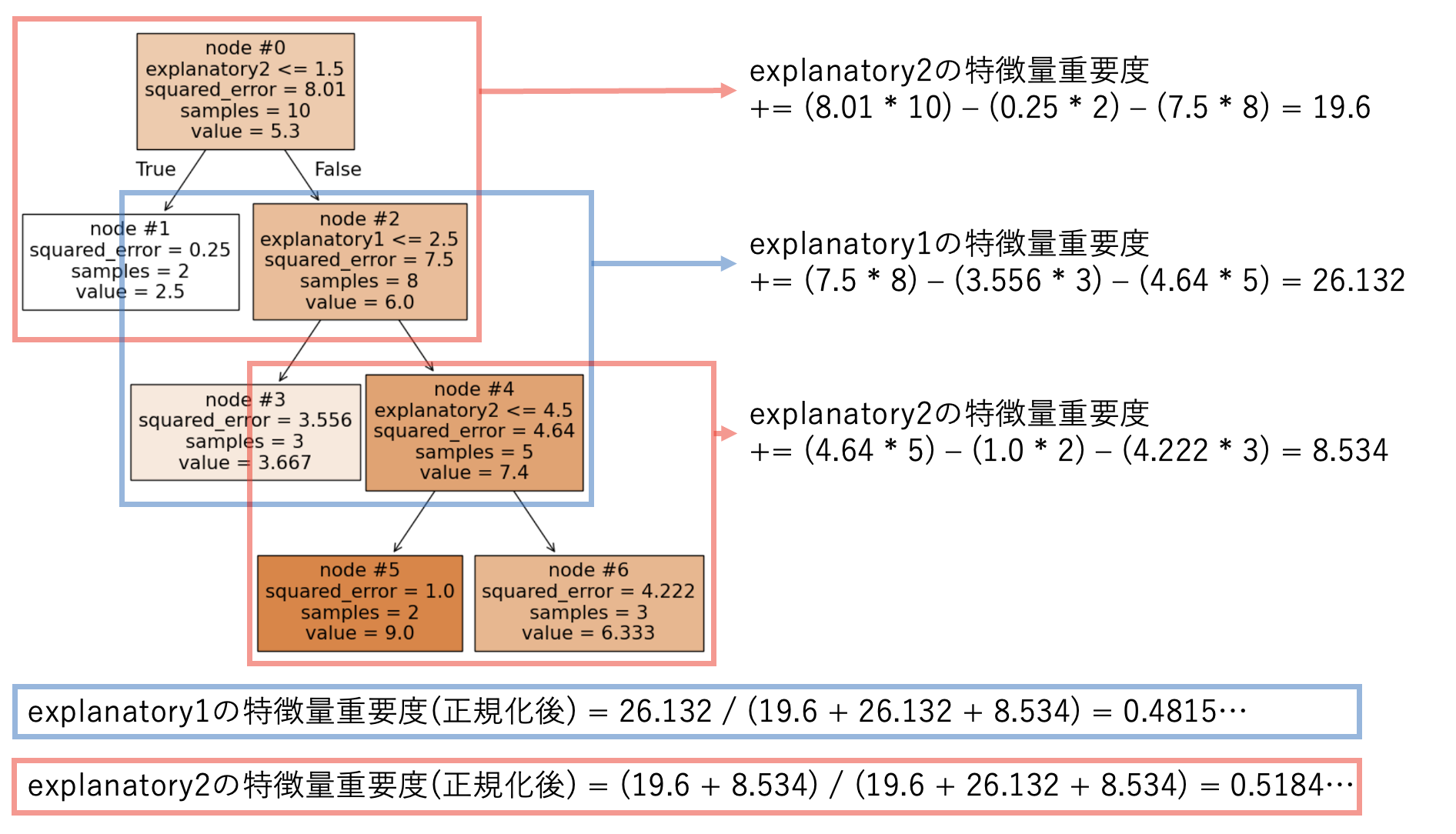
葉以外の各ノードでは、そのノードにおける分割での「データセットが持つ不純度の減少量」を計算します。
「データセットが持つ不純度の減少量」は、各ノードにおける「不純度」を定義し、親ノードの不純度から2つの子ノードの不純度を引く事で算出します。
sklearn.tree.DecisionTreeRegressorでは(そのノードに含まれる学習データのサンプル数)\(\times\)(そのノードに含まれる学習データの目的変数の分散)を不純度とします。
上記の内容をまとめると、ある説明変数の特徴量重要度(正規化前)を算出する式は以下のようになります。
ここで \(i\) はその説明変数を分割の条件に使っているノードの ID 全体を走り、各記号は以下のように定義します。(\(node \ \#i\) は葉ではない事に注意してください。)
学習済みモデルに保存されている特徴量重要度は上記の式を正規化したものになっており、上で学習した DecisionTreeRegressor の場合は以下のように計算できます。
# 各ノードに含まれる学習データのサンプル数 (plot_treeの出力から確認できる値)
node0_n = 10
node1_n = 2
node2_n = 8
node3_n = 3
node4_n = 5
node5_n = 2
node6_n = 3
# 各ノードに含まれる学習データの目的変数の分散 (plot_treeの出力から確認できる値)
node0_squared_error = 8.01
node1_squared_error = 0.25
node2_squared_error = 7.5
node3_squared_error = 3.556
node4_squared_error = 4.64
node5_squared_error = 1.0
node6_squared_error = 4.222
# explanatory1の特徴料重要度(正規化前)
explanatory1_importance = (node2_n * node2_squared_error
- node3_n * node3_squared_error
- node4_n * node4_squared_error)
# explanatory2の特徴料重要度(正規化前)
explanatory2_importance = ((node0_n * node0_squared_error
- node1_n * node1_squared_error
- node2_n * node2_squared_error)
+
(node4_n * node4_squared_error
- node5_n * node5_squared_error
- node6_n * node6_squared_error))
print("explanatory1の特徴量重要度: ", explanatory1_importance / (explanatory1_importance + explanatory2_importance))
print("explanatory2の特徴量重要度: ", explanatory2_importance / (explanatory1_importance + explanatory2_importance))
explanatory1の特徴量重要度: 0.48155382744259767
explanatory2の特徴量重要度: 0.5184461725574024
学習済みモデルに保存されている特徴量重要度は以下のコードで確認でき、上で計算したものと一致している事がわかります。 (plot_treeで出力される数値が小数点第四位までなので、それ未満の値はズレています。)
regressor.feature_importances_
array([0.48157248, 0.51842752])
学習アルゴリズム#
学習時は説明変数に対する条件の真偽で学習データの分割をしていきます。
最初は分割されていない状態から始まります。
学習も、特徴量重要度算出と同じように「不純度の減少量」を用いて、「不純度の減少量」が最大になるように分割の条件を選びます。

分割の条件は説明変数\(j\)と閾値\(t\)に対して「\(j ≤ t\)を満たすか否か」という形で決めます。
具体的には、「\(j ≤ t\)を満たすか否か」という条件での全てのノードの全てのパターンの分割を調べ、以下の式が最大になるようにノード\(i\)と説明変数\(j\)と閾値\(t\)を選びます。
分割を繰り返していき、上記の式が非負になる分割が無い場合に学習が終了します。
決定木回帰の学習は各ノードで全ての分割のパターンを試すため、データ量が増えると、それに比例して計算量が増えていきます。
そのため、木の深さ(根から最も遠い葉までのエッジの数)等に制限をかけて、学習を途中で止める事も多くあります。
小括#
本稿では決定木回帰モデルの解説をしました。
決定木回帰モデル自体を使う事はあまり多くありませんが、決定木の派生であるLightGBMは機械学習コンペティションなどで非常に良く使われています。
LightGBMは決定木と同様に
非線形モデルである
特徴量重要度を算出できる
比較的少ない前処理で実行できる
といった特徴を持ち、さらにアンサンブルする事で精度を高めつつ、計算量を削減する工夫もなされています。
また、決定木は分類問題でも用いられます。分類問題で用いる場合は学習や特徴量重要度算出で使う不純度がジニ不純度等に変わります。
参考文献#
scikit learn公式
更科 明 (Sarashina, Akira)
イノベーションセンター テクノロジー部門 データ分析コンサルティングPJ
Mail: a.sarashina@ntt.com

