周波数解析の基礎

時系列データの解析において、その周期的な成分を特定できればデータの前処理やモデリングの過程における有益な示唆を得ることができます。例えばARモデルやMAモデルといった古典的な時系列モデリングの挙動を記述する上でこれらモデルの定める周波数スペクトルは重要な役割を果たします。また、システムの周波数領域における挙動を解析し制御することは古典制御論における本質的な課題の一つでもあります。

本稿では系列データの周期成分を抽出するための基本的な枠組みであるフーリエ変換、およびその離散的な拡張についてSymPy, SciPyでの実装を交えつつ概説します。また、合わせて離散的な時刻で観測された系列（離散時間の信号）の周波数成分を考える上での注意点についても簡単に触れます。

特に断りのない限り、本項では時刻の関数 \(x ( t )\) （あるいは時刻を添字とする列 \(x_n\) ）を周波数 (frequency) や角周波数 (angular frequency) と呼ばれる量で表現する場合のことを考えます。このため \(x ( t )\) （や \(x_n\) ）のことを信号処理の用語で単に信号 (signal) と呼ぶことがあります。

フーリエ変換の基礎

解析対象のセンサーデータは一般に離散的な時刻で測定されたものですが、ひとまず連続的な時刻の関数 \(x ( t )\) の周期成分を抽出することについて考えます。本項では

• 関数 \(x ( t )\) が周期関数である場合に、これを異なる周波数の正弦波の級数に分解するフーリエ級数、および

• 関数 \(x ( t )\) が一般の非周期関数である場合に、これを周波数領域での正弦波の積分として表現するフーリエ変換

について要点をまとめ、時間領域の連続関数を周波数領域で表現する方法について復習します。本項では数学的な導出の詳細は避け、必要最低限の解説と例示にとどめます。

動画: 時間領域と周波数領域の関係の可視化（Wikimedia Commonsのファイルより引用）

フーリエ級数

関数 \(x ( t )\) が周期 \(T\) の周期関数である場合、即ち任意の \(t \in \mathbf{R}\) に対して

\[ x ( t ) = x ( t - T ) \]

が成り立つ場合、 \(x ( t )\) が一定の制約を満たせば

\[ x ( t ) = \frac{a_0}{2} + \sum_{k = 1}^\infty \left( a_k \cos \left( \frac{2 \pi k}{T} t \right) + b_k \sin \left( \frac{2 \pi k}{T} t \right) \right) \]

のようにこれを三角関数の無限級数として表現することができます。この表現を フーリエ級数 (Fourier series) または フーリエ級数展開 (Fourier series expansion) と呼びます。ここで各係数 \(a_k\) および \(b_k\) は積分

\[\begin{split} a_k = \frac{2}{T} \int_{- \frac{T}{2}}^{\frac{T}{2}} x ( t ) \cos \left( \frac{2 \pi k}{T} t \right) d t \text{,} \\ b_k = \frac{2}{T} \int_{- \frac{T}{2}}^{\frac{T}{2}} x ( t ) \sin \left( \frac{2 \pi k}{T} t \right) d t \end{split}\]

によって求めることができます。

上記の無限級数の各項を詳しく観察すると、

• \(k = 0\) の項は定数項、

• \(k \ge 1\) の項は（三角関数の合成公式を思い出すと）基本周期 \(T / k\) 、振幅 \(\sqrt{a_k^2 + b_k^2}\) の三角関数

になっていることが分かります。これらはいずれも周期 \(T\) の周期関数です。即ち、フーリエ級数は周期 \(T\) の周期関数を定数項と基本周期 \(T, T / 2, T / 3, \ldots\) の三角関数の和に分解して表現したものと思うことができます。

ところで、 \(i\) を虚数単位とすればオイラーの公式

\[ e^{- i \theta} = \cos \theta + i \sin \theta \]

から複素指数関数を用いて上記の無限級数を書き直すことができて、

\[ x ( t ) = \sum_{k = - \infty}^\infty c_k e^{i \frac{2 \pi k }{T} t} \]

と表現することもできます。この場合、各係数 \(c_k\) は実軸上での複素積分

\[ c_k = \frac{1}{T} \int_{- \frac{T}{2}}^\frac{T}{2} x ( t ) e^{- i \frac{2 \pi k}{T} t} dt \]

によって求めることができます。無限級数の虚部は添字の正負で相殺されて消失することに注意してください。

例（周期関数のフーリエ級数展開）

関数 \(x ( t )\) を

\[\begin{split} x ( t ) = \begin{cases} t^4 - t^2 & - 1 \le t < 1 \\ x ( t - 2 \lfloor \frac{t + 1}{2} \rfloor ) & \text{otherwise} \end{cases} \end{split}\]

で定めると、これは基本周期 \(T = 2\) の（連続な）周期関数になっています。この関数のフーリエ級数展開をSymPyで具体的に計算し、打ち切った有限級数の定める関数を描画してみましょう。

from sympy import fourier_series, plot, Symbol

t = Symbol("t", real=True)
x = t**4 - t**2  # tを(-1, 1)の範囲に限って周期関数とみなす
fs = fourier_series(
    x, (t, -1, 1)
)  # 展開の実行、デフォルトではk=3以降の項を捨てた級数を表示

fs.truncate(4)  # k=4以降の項を捨てた級数を表示

\[\displaystyle \left(- \frac{4}{\pi^{2}} + \frac{48}{\pi^{4}}\right) \cos{\left(\pi t \right)} + \left(- \frac{3}{\pi^{4}} + \frac{1}{\pi^{2}}\right) \cos{\left(2 \pi t \right)} + \left(- \frac{4}{9 \pi^{2}} + \frac{16}{27 \pi^{4}}\right) \cos{\left(3 \pi t \right)} - \frac{2}{15}\]

import matplotlib.pyplot as plt


plt.rcParams["axes.grid"] = True

# k=Kまでの項で近似した関数を表示

_lims = {"xlim": (-1.2, 1.2), "ylim": (-0.5, 0.5)}

p = plot(x, **_lims, line_color="C0", label="x(t)", legend=True, show=False)
p.append(plot(fs.truncate(1), **_lims, line_color="C1", label="K=0", show=False)[0])
p.append(plot(fs.truncate(2), **_lims, line_color="C2", label="K=1", show=False)[0])
p.append(plot(fs.truncate(3), **_lims, line_color="C3", label="K=2", show=False)[0])
p.append(plot(fs.truncate(4), **_lims, line_color="C4", label="K=3", show=False)[0])
p.show()

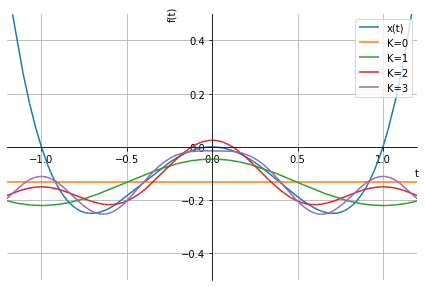
実際の \(x ( t )\) （青線）は上図の \([ -1, 1 )\) の範囲をこの外でも繰り返したような形になっています。この図からもフーリエ級数がどのように周期関数を表現しているかを確認することができます。

フーリエ変換

関数 \(x ( t )\) が非周期関数の場合でも、基本周期 \(T, T / 2, T / 3, \ldots\) なる正弦波の級数に替えて周波数での積分を考えることで同様に \(x ( t )\) を三角関数に分解した表現を行うことができます。即ち、一定の条件を満たす（周期的とは限らない）実変数の関数 \(x ( t )\) について、同じく実変数の関数 \(X ( f )\) を

\[ \hat{x} ( f ) = \int_{- \infty}^\infty x ( t ) e^{- 2 \pi i f t} d t \]

によって定めれば

\[ x ( t ) = \int_{- \infty}^\infty \hat{x} ( f ) e^{2 \pi i f t} d f \]

として表現することができます。ただし積分はいずれも実軸上での複素積分として行います。このとき、上記の元の関数 \(x ( t )\) から関数 \(\hat{x} ( f )\) への変換を フーリエ変換 (Fourier transform) と呼び、関数 \(\hat{x} ( f )\) から関数 \(x ( t )\) への変換を 逆フーリエ変換 (inverser Fourier transform) と呼びます。また、元の関数 \(x ( t )\) の入力領域を 時間領域 (time domain) 、変換した関数 \(\hat{x} ( f )\) の入力領域を 周波数領域 (frequency domain) とそれぞれ呼び分けることがあります。

なお、信号処理や制御工学の分野では周波数 \(f\) の代わりに角周波数 \(\omega = 2 \pi f\) を用いた

\[ X ( \omega ) = \int_{- \infty}^\infty x ( t ) e^{- i \omega t} d t \]

および

\[ x ( t ) = \frac{1}{2 \pi} \int_{- \infty}^\infty X ( \omega ) e^{i \omega t} d \omega \]

の標識の方がよく使われます。このとき \(\hat{x} ( f ) = X ( 2 \pi f )\) の関係になっていることに注意してください。この変換にもフーリエ変換および逆フーリエ変換の用語を充てます。

いずれの標識でもフーリエ逆変換の被積分項は複素指数関数によって周期 \(1 / f = 1 / ( 2 \pi \omega )\) で振動する関数となっており、フーリエ変換によって得た関数 \(\hat{x} ( f )\) （または \(X ( \omega )\) ）は元の関数 \(x ( t )\) の周波数 \(f\) （または角周波数 \(\omega\) ）で振動する成分を並べたものであり、即ち元の関数 \(x ( t )\) を周波数（または角周波数）の異なる振動に分解して表現したものと考えることができます。直感的には、非周期関数を周期 \(T \to \infty\) の周期関数と思った際にフーリエ級数で和を取る周波数の間隔 \(k / T\) が無限に小さくなり、それに伴ってフーリエ級数の総和を積分で置き換えたものが逆フーリエ変換だと思って構いません。

なお、厳密にはこれら通常の複素積分によるフーリエ変換の定義では \(x ( t )\) が絶対可積分である ( \(\int_{- \infty}^\infty | x ( t ) | d t < \infty\) となる) ことが要請され、特に \(x ( t ) = \sin t\) をはじめとする一般の周期関数についてフーリエ変換を定義することができません。これらの関数にフーリエ変換を定義するにはシュワルツ超関数の文脈で議論する必要があり、この前提で周期関数

\[ x ( t ) = \sum_{k = - \infty}^\infty c_k e^{i \frac{2 \pi k }{T} t} \]

をフーリエ変換すれば

\[ \hat{x} ( f ) = \sum_{k = - \infty}^\infty c_k \delta \left( f - \frac{k}{T} \right) \]

または

\[ X ( \omega ) = \sum_{k = - \infty}^\infty c_k \delta \left( \omega - \frac{2 \pi k}{T} \right) \]

という表現を得ることができます。ただし \(\delta ( f )\) はディラックのデルタ関数で、任意の連続関数 \(\hat{y} ( f )\) に対して

\[ \int_{- \infty}^\infty \hat{y} ( f ) \delta ( f ) d f = \hat{y} ( 0 ) \]

を満たすものとして定義されます（直感的には積分領域上の1点に重みを与える関数）。これら \(\hat{x} ( f )\) ないし \(X ( \omega )\) を適切にフーリエ逆変換すれば元の周期関数を得ることができ、この意味においてフーリエ変換はフーリエ級数の非周期関数への拡張と思うことができます。

例（正規分布確率密度関数の逆フーリエ変換）

正規分布 \(\mathrm{N} ( \mu, \sigma^2 )\) の確率密度関数

\[ p ( x; \mu, \sigma ) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left( - \frac{( x - \mu )^2}{2 \sigma^2} \right) \]

の逆フーリエ変換を考えます。

from sympy import Symbol, Abs
from sympy.stats import density, Normal
from sympy.integrals import fourier_transform, inverse_fourier_transform

mu = Symbol("mu", real=True)  # 正規分布の平均
sigma = Symbol("sigma", positive=True)  # 正規分布の標準偏差
X = Normal("X", mean=mu, std=sigma)  # 正規分布
x = Symbol("x", real=True)  # 正規分布の確率密度関数の変数
pdf = density(X)(x)  # 正規分布の確率密度関数
pdf

\[\displaystyle \frac{\sqrt{2} e^{- \frac{\left(- \mu + x\right)^{2}}{2 \sigma^{2}}}}{2 \sqrt{\pi} \sigma}\]

# 標準正規分布 N(0, 1) の場合の確率密度関数のプロット
_lims = {"xlim": (-5.0, 5.0), "ylim": (-0.1, 0.5)}
plot(pdf.subs({mu: 0, sigma: 1}), **_lims, label="PDF of N(0, 1)", legend=True)

<sympy.plotting.plot.Plot at 0x115140490>

SymPyでは fourier_transform 関数で（数学的な意味での）フーリエ変換を、 inverse_fourier_transform 関数で逆フーリエ変換をそれぞれ実行することができます。

t = Symbol("t", real=True)  # 逆フーリエ変換した関数の変数
if_pdf = inverse_fourier_transform(pdf, x, t)  # 逆フーリエ変換の実行
if_pdf

\[\displaystyle e^{2 \pi t \left(i \mu - \pi \sigma^{2} t\right)}\]

# 標準正規分布 N (0, 1) の場合のプロット（ mu = 0 では実軸上で実数値を取る関数になる）
_lims = {"xlim": (-1.2, 1.2), "ylim": (-0.1, 1.2)}
plot(
    if_pdf.subs({mu: 0, sigma: 1}), **_lims, label="IFT of PDF of N(0, 1) ", legend=True
)

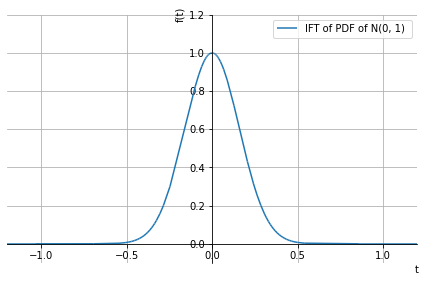
<sympy.plotting.plot.Plot at 0x127b69c50>

一般に、確率変数 \(X\) に対して定義される関数 \(\varphi ( t ) = \mathrm{E} [ \exp ( i t X ) ]\) を \(X\) の特性関数 (characteristic function) と呼びます。いま \(X\) の確率密度関数 \(p ( x )\) が定義できる場合は

\[ \varphi ( t ) = \int_{- \infty}^\infty \exp ( i t x ) p ( x ) d x \]

となるので、特性関数 \(\varphi ( t )\) は（適当な変数変換の下で）確率密度関数 \(p ( x )\) の逆フーリエ変換になっており、その逆変換（すなわち対応するフーリエ変換）として

\[ p ( x ) = \frac{1}{2 \pi} \int_{- \infty}^\infty \exp ( - i t x ) \varphi ( t ) d x \]

の関係があることが分かります。

正規分布の特性関数は次のように計算できます：

from sympy import pi  # 円周率
from sympy.integrals.transforms import (
    _fourier_transform,
)  # 係数を指定できるフーリエ変換型の変換

chf = _fourier_transform(pdf, x, t, a=1, b=1, name="")  # 特性関数
chf

\[\displaystyle e^{\frac{t \left(2 i \mu - \sigma^{2} t\right)}{2}}\]

ここで _fourier_transform 関数は

\[ x ( t ) \mapsto \tilde{x} ( u ) = a \int_{- \infty}^\infty x ( t ) e^{- b i u t} d t \]

なるフーリエ変換型の変換を実行する関数で、SymPyで工学的な意味でのフーリエ変換・逆フーリエ変換を行う場合もこの関数を用いて計算することになります。

また、特性関数を（対応する適当な変数変換の下で）フーリエ変換すれば元の確率密度関数に戻ることも確認できます：

pdf_ = _fourier_transform(
    chf, t, x, a=1 / (2 * pi), b=1, name=""
)  # 特性関数のフーリエ変換
pdf_

\[\displaystyle \frac{\sqrt{2} e^{- \frac{\left(\mu + x\right)^{2}}{2 \sigma^{2}}}}{2 \sqrt{\pi} \sigma}\]

例（定数関数と三角関数のフーリエ変換）

定数関数 \(x ( t ) = 1\) のフーリエ変換は、ディラックのデルタ関数 \(\delta\) を用いて

\[ \hat{x} ( f ) = \delta ( f ) \]

と表現できます。また、三角関数 \(x ( t ) = \cos ( a t )\) のフーリエ変換は

\[ \hat{x} ( f ) = \frac{1}{2} \left( \delta \left( f - \frac{a}{2 \pi} \right) + \delta \left( f + \frac{a}{2 \pi} \right) \right) \]

と、 \(x ( t ) = \sin ( a t )\) のフーリエ変換は

\[ \hat{x} ( f ) = \frac{1}{2} i \left( \delta \left( f - \frac{a}{2 \pi} \right) - \delta \left( f + \frac{a}{2 \pi} \right) \right) \]

とそれぞれ表現できます。

なお、SymPyの fourier_transform はこれら周期関数のフーリエ変換を（特殊関数の意味で）正しく計算できないので注意が必要です。

from sympy import cos

t = Symbol("t", real=True)  # 時間領域の変数
x = cos(t)
f = Symbol("f", real=True)  # 周波数領域の変数
fourier_transform(x, t, f)

\[\displaystyle 0\]

フーリエ変換の離散化

ここまでの議論では連続的な時刻の関数 \(x ( t )\) を周波数成分に分解して表現することを考えていましたが、実用上興味のあるデータは1秒毎や1分毎など離散的な時刻でのみ観測されているものがほとんどです。

本項ではデータが一定の周期 \(\Delta t \in \mathbf{R}\) で観測されているものとし、（潜在的には連続時間の）信号 \(x ( t )\) の値も離散的な時刻 \(n \Delta t\) ( \(n \in \mathbf{Z}\) ) での \(x_n = x ( n \Delta t )\) のみが得られているものとします。このように連続信号 \(x ( t )\) を離散時間の信号 \(x_n\) に変換する処理を 標本化 (sampling) といいます。また周期 \(\Delta t\) を 標本化周期 (sampling period, sampling interval) といい、その逆数 \(1 / \Delta t\) を 標本化周波数 (sampling frequency, sampling rate) といいます。

import numpy as np

fig, ax = plt.subplots(figsize=(10, 5))

t = np.arange(0.0, 20.0, 0.01)
t_samples = np.arange(0.0, 21.0, 2.0)
x = np.cos(t)
x_samples = np.cos(t_samples)

ax.plot(t, x, ls="--", c="C0", label="original signal")
ax.scatter(t_samples, x_samples, c="C3", label="sampled signal")
ax.set_xticks(t_samples)
ax.set_xlabel("t")
ax.set_ylabel("x(t)")
ax.legend()

plt.show()

エイリアシングと標本化定理

標本化された信号の周波数成分を考える際に注意すべき現象として エイリアシング (aliasing) が存在します。基本周期 \(1 / f\) の三角関数 \(x ( t; f ) = \cos ( 2 \pi f t )\) を標本化周期 \(f_s = 1 / \Delta t\) で \(x_{n, f} = x (n \Delta t; f)\) として標本化することを考えます。このとき \(m \in \mathbf{Z}\) に対して \(f ( m ) = | f - m f_s |\) とおくと、例えば

\[ x_{n, f ( m )} = \cos ( 2 \pi f ( m ) n \Delta t ) = \cos ( | 2 \pi f n \Delta t - 2 \pi m n | ) = \cos ( 2 \pi f n \Delta t ) = x_{n, f} \]

となるように、標本化された離散時間の信号においてこれらの周波数は区別できません。このため標本化された信号を通常の方法で復元しようとすると元の連続信号に存在した高周波成分がより低周波の雑音として現れてしまうことがあり、このような現象がエイリアシングと呼ばれます。

fig, ax = plt.subplots(figsize=(10, 5))

t = np.arange(0.0, 20.0, 0.01)
t_samples = np.arange(0.0, 21.0, 2.0)  # fs = 1/2 でサンプリング
x0 = np.cos(t)  # f = 1/(2 pi) の正弦波; 上式で m = 0 の場合
x1 = np.cos(np.abs(1 - 2 * np.pi * 1 * 0.5) * t)  # 上式で m = 1 の場合の正弦波
x2 = np.cos(np.abs(1 - 2 * np.pi * 2 * 0.5) * t)  # 上式で m = 2 の場合の正弦波
x_samples = np.cos(t_samples)

ax.plot(t, x0, ls="--", c="C0", label="m=0")
ax.plot(t, x1, ls="--", c="C1", label="m=1")
ax.plot(t, x2, ls="--", c="C2", label="m=2")
ax.scatter(t_samples, x_samples, c="C3", label="sampled signal")
ax.set_xticks(t_samples)
ax.set_xlabel("t")
ax.set_ylabel("x(t)")
ax.legend()

plt.show()

例えば上図の場合、3つの連続信号 \(\cos t, \cos ( | 1 - \pi | t ), \cos ( | 1 - 2 \pi | t )\) （それぞれ青破線、橙破線、緑破線）は \(t = 0, 2, 4, 6, \ldots\) （赤点）で同じ値を取ります。従って、もし緑破線の連続信号を赤点で標本化したとしても青破線や橙破線の信号と区別がつかず、人間の感覚や多くのアルゴリズムでは最も周波数が低い青破線の信号が復元されてしまうということが起こるのです。

一般の連続信号 \(x ( t )\) について考えると、 \(x ( t )\) に存在する最大の周波数成分が \(f_M\) の場合は標本化周波数を \(f_s > 2 f_M\) と設定することでエイリアシングの影響を避けることができます。実はこのとき標本化した信号 \(x_n\) から元の信号 \(x ( t )\) を完全に復元できることが知られており、 標本化定理 と呼ばれています。また、標本化周波数 \(f_s\) が固定されている場合、標本化によって元の信号の \(f_s / 2\) より大きい周波数成分の情報は実質的に失われます。この周波数 \(f_s / 2\) を ナイキスト周波数 (Nyquist frequency) といいます。

離散時間フーリエ変換

離散時間の信号 \(x_n\) に対して、関数 \(X ( \omega )\) を

\[ X ( \omega ) = \sum_{n = - \infty}^\infty x_n e^{- i \omega n} \]

で定めれば、

\[ x_n = \frac{1}{2 \pi} \int_{- \pi}^\pi X ( \omega ) e^{i \omega n} d \omega \]

と表現することができます。このとき \(x_n\) から \(X ( \omega )\) への変換を 離散時間フーリエ変換 (discrete-time Fourier transform, DTFT) と呼び、 \(X ( \omega )\) から \(x_n\) への変換を 逆離散時間フーリエ変換　(inverse discrete-time Fourier transform, IDTFT) と呼びます。この \(X ( \omega )\) は基本周期 \(2 \pi\) の周期関数になっていることに注意してください。

直感的な解釈としては、離散時間信号 \(x_n\) の標本化周期を \(\Delta t = 1\) としてディラックのデルタ関数を用いた連続信号

\[ x ( t ) = \sum_{n = \infty}^\infty x_n \delta ( t - n ) \]

に通常のフーリエ変換を施したものが離散時間フーリエ変換になっています。 このため逆離散時間フーリエ変換で \(\omega\) の積分範囲を実軸全体に取ると元の \(x_n\) ではなくこの連続信号 \(x ( t )\) が復元されてしまい、 \(t = n\) で有限の値を持ちません。そこでフーリエ級数展開の係数 \(c_n\) を求めた場合と同様に \(\omega\) の積分範囲を \(X ( \omega )\) の1周期分に限定し、 \(x_n\) の値を求めるようにしています。この意味において、離散時間フーリエ変換はフーリエ級数展開における時間領域と周波数領域の役割を入れ替えたものになっていると思うことができます。

離散フーリエ変換

以上の議論より

• 時間領域で周期的な信号は周波数領域で離散的な信号に対応し (cf. フーリエ級数展開)、

• 時間領域で離散的な信号は周波数領域で周期的な信号に対応する (cf. 離散時間フーリエ変換)

ことが分かりました。従って、時間領域で周期的かつ離散的な信号は周波数領域でも周期的かつ離散的な信号に対応することになり、どちらの領域においても、またそれらを相互に変換する操作においても計算機上で極めて扱いやすくなることが想定されます。

有限長の離散時間信号 \(x_0, \ldots, x_{N - 1}\) に対して、対応する系列 \(X_0, \ldots, X_{N - 1}\) を

\[ X_k = \sum_{n = 0}^{N - 1} x_n e^{- i \frac{2 \pi k}{N} n} \]

で定めると

\[ x_n = \frac{1}{N} \sum_{k = 0}^{N - 1} X_k e^{i \frac{2 \pi k}{N} n} \]

と表現することができます。このとき \(x_n\) から \(X_k\) への変換を 離散フーリエ変換 (discrete Fourier transform, DFT) と呼び、 \(X_k\) から \(x_n\) への変換を 逆離散フーリエ変換 (inverse discrete Fourier transform, IDFT) と呼びます。どちらの系列 \(x_n\) および \(X_k\) も周期 \(N\) の系列として \(n \le -1, N \le n\) および \(k \le -1, N \le k\) の範囲にそれぞれ拡張して考えることが可能です。

離散時間信号 \(x_n\) の標本化周期を \(\Delta t\) としたとき、各 \(X_k\) は元の信号の周波数 \(k / ( N \Delta t )\) の成分を抽出したものと思うことができます。ただし上述のエイリアシングの問題から \(1 / (2 \Delta t)\) より大きい周波数の成分（即ち系列 \(X_k\) のうち後ろ半分）は実用上の意味がなく、しばしば無視されます。

離散フーリエ変換および逆離散フーリエ変換は 高速フーリエ変換 (fast Fourier transform, FFT) および 逆高速フーリエ変換 (inverse fast Fourier transform, IFFT) と呼ばれるアルゴリズムで高速に計算することができます。FFTおよびIFFTの実装は例えばSciPyの scipy.fft モジュールなどに格納されており、簡単に利用することができます。

例（正弦波とエイリアシング）

離散フーリエ変換におけるエイリアシングの例を確認してみましょう。標本化周波数 \(f_s = 16\) として、連続信号

\[ x ( t ) = \cos ( 2 \pi | f - m f_s | t ) \]

を \(m = 0, 1, 2\) について考えます。簡単のため \(f = 1\) とし、標本化は時刻 \(t_n = n / 16 f_s\) ( \(n = 0, \ldots, 15\) ) で行ったものとします。このときエイリアシングが発生して離散信号 \(x_n = x ( t_n )\) およびその離散フーリエ変換 \(X_k\) は \(N\) によって区別できないはずですが、このことを数値的に確認してみましょう。

from scipy.fft import fft, ifft

f = 1.0
fs = 16.0
n = np.arange(0, 16)

x0 = np.cos(2 * np.pi * f * n / fs)  # m = 0
x1 = np.cos(2 * np.pi * np.abs(f - 1 * fs) * n / fs)  # m = 1
x2 = np.cos(2 * np.pi * np.abs(f - 2 * fs) * n / fs)  # m = 2

X0 = fft(x0)
X1 = fft(x1)
X2 = fft(x2)

\(m = 0, 1, 2\) の連続信号をそれぞれ標本化した離散信号 \(x_n\) をプロットすると次のようになります：

fig, ax = plt.subplots(figsize=(10, 5))
ax.bar(n - 0.2, x0, width=0.2, color="C0", label="m=0")
ax.bar(n, x1, width=0.2, color="C1", label="m=1")
ax.bar(n + 0.2, x2, width=0.2, color="C2", label="m=2")
ax.set_xticks(np.arange(0, 16))
ax.set_title("")
ax.set_xlabel("n")
ax.set_ylabel("xn")
ax.legend()

plt.show()

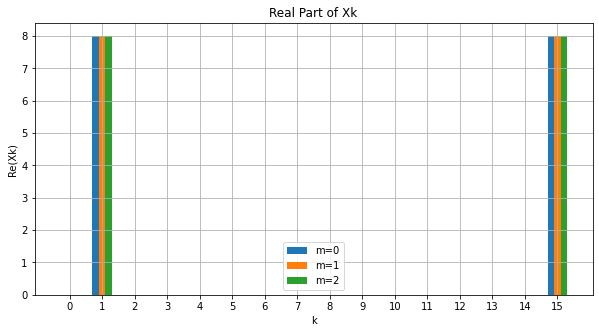
同様に、 \(m = 0, 1, 2\) に対応する離散時間信号を離散フーリエ変換した \(X_k\) をプロットすると次のようになります：

fig, ax = plt.subplots(figsize=(10, 5))
ax.bar(n - 0.2, X0.real, width=0.2, color="C0", label="m=0")
ax.bar(n, X1.real, width=0.2, color="C1", label="m=1")
ax.bar(n + 0.2, X2.real, width=0.2, color="C2", label="m=2")
ax.set_xticks(np.arange(0, 16))
ax.set_title("Real Part of Xk")
ax.set_xlabel("k")
ax.set_ylabel("Re(Xk)")
ax.legend()

plt.show()

fig, ax = plt.subplots(figsize=(10, 5))
ax.bar(n - 0.2, X0.imag, width=0.2, color="C0", label="m=0")
ax.bar(n, X1.imag, width=0.2, color="C1", label="m=1")
ax.bar(n + 0.2, X2.imag, width=0.2, color="C2", label="m=2")
ax.set_xticks(np.arange(0, 16))
ax.set_title("Imaginary Part of Xk")
ax.set_xlabel("k")
ax.set_ylabel("Im(Xk)")
ax.legend()

plt.show()

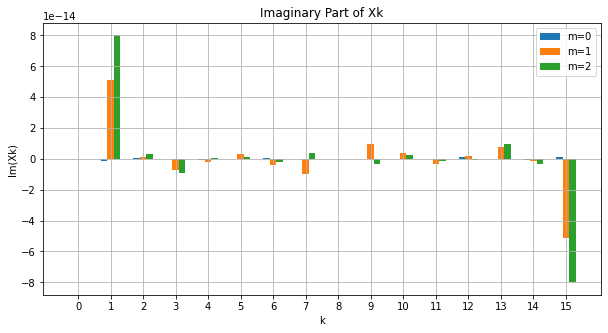
虚部については縦軸のスケールを考えればほぼゼロ（数値計算上の誤差であり、本来は真にゼロ）であり、 \(m = 0, 1, 2\) のいずれも周波数成分は \(k = 1, 15\) に集中しています。このうち \(k = 1\) に対応する周波数は \(k / f_s N = 1 / f_s N = 1 = f\) となっており、確かに \(m = 0\) なる正弦波の基本周期が抽出されています。一方 \(k = 15\) に対応する周波数は \(m = 1\) に対応するものであり、実際 \(k / f_s N = 15 / f_s N = 15 = | f - f_s |\) が成り立っていることが分かります。この周波数はナイキスト周波数 \(f_s / 2 = 8\) よりも大きく、実質的には意味のない（あるいは \(k = 1\) のものと重複した）情報になっています。

小括

図: フーリエ級数展開・フーリエ変換などの関係

本稿では周波数解析の基礎としてフーリエ級数展開、フーリエ変換、離散時間フーリエ変換、離散フーリエ変換の4つについて簡単に説明し、あわせて離散時間信号の周波数を扱う場合の本質的な問題であるエイリアシングについて解説しました。これらの級数展開・変換はいずれも関数（または信号）の周波数領域での表現を考える上での基本となるものですが、いずれも元の関数の全体にわたるもので、音声信号や複雑な時系列データのように時刻によって周波数成分が変化するような信号の表現には十分でありません。続く解説では、このような信号における周波数成分の変化を表現する方法について説明します。

参考文献

• やる夫で学ぶディジタル信号処理

  • 会話劇の形式でフーリエ解析、ラプラス変換、線形システム論、制御論などを学び直すことのできるサイト

• Wikipedia「フーリエ変換」

  • 引用した時間領域・周波数領域の関係の動画はこのページなどに掲載