ガウス過程回帰モデルの基礎#
本稿では、統計的機械学習で用いられる強力なモデルの一つであるガウス過程回帰モデルについて解説します。ガウス過程回帰モデルはガウス過程というランダムな関数の確率分布を利用した回帰モデルで、回帰曲面の関数形を具体的に指定することなしにデータの情報を利用して回帰問題の推論を行うことができます。本稿ではガウス過程についての確率過程論からの厳密な定式化は省き、多変量正規分布のアナロジーからの直感的な描写を目指します。
ガウス分布からガウス過程まで#
ガウス過程 (Gaussian process; GP) とは、直感的には正規分布 (ガウス分布) をランダムな関数の空間に拡張したものと思うことができます。まずはグラフを用いてガウス分布とガウス過程のつながりを追いながら、ランダムな関数とはどのようなものか、またランダムな関数の確率分布をどのように取り扱えばいいのかについて簡単に確認してみましょう。
正規分布#
正規分布とは、実数 \(\mathbf{R}\) 上の確率分布でその確率密度関数が
の形で書けるもののことでした。ここで \(\mu \in \mathbf{R}\) と \(\sigma^2 > 0\) は正規分布のパラメータです。確率変数 \(Y_0\) が上記の正規分布に従うことを \(Y_0 \sim \mathrm{N} ( \mu, \sigma^2 )\) と書くことにしましょう。このとき \(Y_0\) の平均は \(\mathrm{E} [ Y_0 ] = \mu\) となり、分散は \(\mathrm{V} ( Y_0 ) = \sigma^2\) となります。
正規分布がどのような形をしているのか、実際にSciPyとMatplotlibを使って描画してみましょう:
import warnings
warnings.filterwarnings('ignore')
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm, multivariate_normal
np.random.seed(42)
y = norm.rvs(loc=0, scale=1, size=100)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 5))
grid_y = np.arange(-3., 3., 0.1)
ax1.plot(grid_y, norm.pdf(grid_y, loc=0., scale=1.), color='C0', label='Gaussian PDF')
ax1.scatter(y, np.zeros_like(y), alpha=0.1, color='red', label='observation')
ax1.set_xlim(-3., 3.)
ax1.set_xlabel('y')
ax1.set_ylabel('density')
ax1.legend()
ax2.scatter(np.full_like(y, fill_value=0.), y, alpha=0.1, color='red')
ax2.set_xlabel('index')
ax2.set_ylabel('observed value')
fig.show()
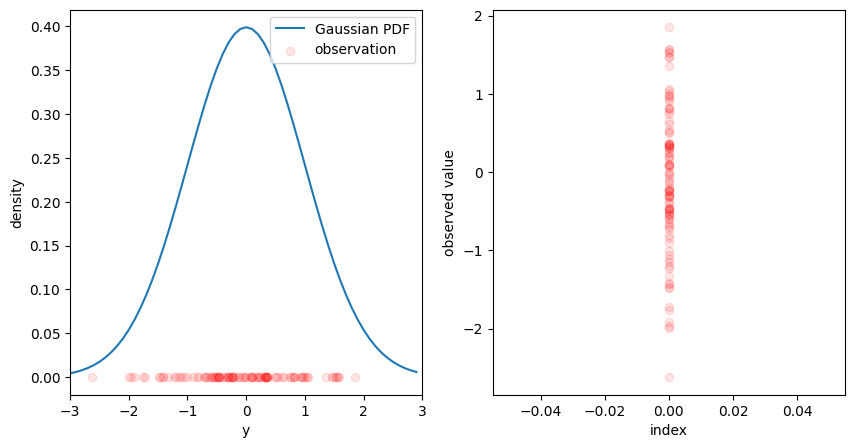
左の図は正規分布 \(\mathbf{N} ( 0, 1 )\) について確率密度関数と標本100個を描画したものです。また、右の図は同じ標本100個を縦に並べたものです。
多変量正規分布#
正規分布はユークリッド空間 \(\mathbf{R}^d\) 上の確率分布に拡張することができます。確率密度関数が
の形で書ける \(\mathbf{R}^d\) 上の確率分布を多変量正規分布と呼びます。ここで、ベクトル \(\mu = ( \mu_0, \ldots, \mu_{d - 1} )\in \mathbf{R}^d\) と半正定値行列 \(\Sigma = ( \sigma_{i j} )_{i, j \in \{ 0, \ldots, d-1 \}} \in \mathbf{R}^{d \times d}\) は多変量正規分布のパラメータです。確率変数のベクトル \(\mathbf{Y} = ( Y_0, \ldots, Y_{d - 1} )^\mathrm{T}\) が上記の多変量正規分布に従うことを \(\mathrm{N}_d ( \mu, \Sigma )\) と書くことにしましょう。このとき各 \(Y_i\) の期待値は \(\mathrm{E} [ Y_i ] = \mu_i\) となり、分散は \(\mathrm{V} [ Y_i ] = \sigma_{i i}\) となります。また、共分散は \(\mathrm{Cov} ( Y_i, Y_j ) = \sigma_{i j}\) となります。
多変量正規分布がどのような形をしているのか、 \(d = 2\) の場合で実際にSciPyとMatplotlibを使って描画してみましょう:
np.random.seed(42)
n_dim = 2
v = np.fromfunction(
function=lambda i, j: np.exp(- (i - j) ** 2 / 2.),
shape=(n_dim, n_dim),
)
y = multivariate_normal.rvs(cov=v, size=100)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 5))
grid_y1 = np.arange(-3., 3., 0.1)
grid_y2 = np.arange(-3., 3., 0.1)
grid_y12 = np.array(np.meshgrid(grid_y1, grid_y2))
p_y12 = np.apply_along_axis(lambda grid: multivariate_normal.pdf(grid, cov=v), 0, grid_y12)
_cntr = ax1.contour(grid_y1, grid_y2, p_y12, colors='C1')
_l_cntr, _ = _cntr.legend_elements()
_sctr = ax1.scatter(y[:, 0], y[:, 1], alpha=0.1, color='red')
ax1.set_xlim(-3., 3.)
ax1.set_xlabel('y1')
ax1.set_ylabel('y2')
ax1.legend([_l_cntr[0], _sctr], ['Gaussian PDF contour', 'observation'])
for j in range(y.shape[1]):
ax2.scatter(np.full_like(y[:, j], fill_value=j), y[:, j], alpha=0.1, color='red')
for i in range(y.shape[0]):
ax2.plot(np.arange(0, n_dim, 1), y[i, :], alpha=0.1, color='red')
ax2.set_xlabel('index')
ax2.set_ylabel('observed value')
fig.show()
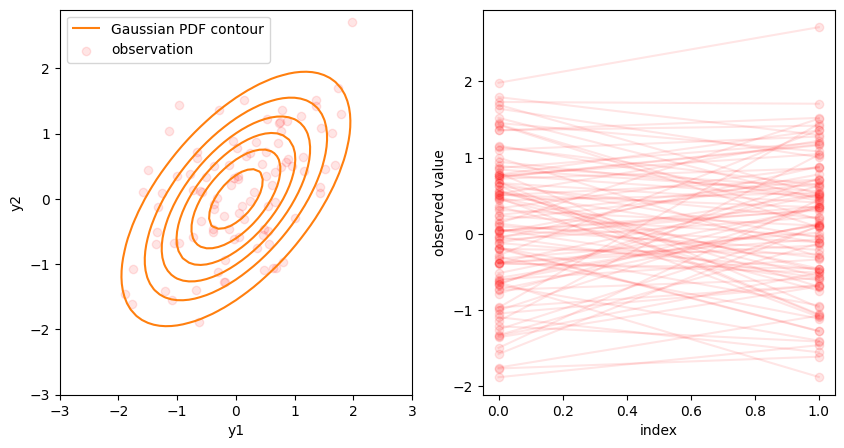
左の図はパラメータ
なる多変量正規分布 \(\mathrm{N}_2 ( \mathbf{0}, \Sigma )\) について、確率密度関数の等高線と標本100個を描画したものです。右の図は同じ標本100個を確率変数の添字 \(i \in \{0, 1 \}\) ごとに縦に並べ、対応する標本を線で繋いだものです。
では、 \(d = 10\) の場合はどうなるでしょうか:
np.random.seed(42)
n_dim = 10
v = np.fromfunction(
function=lambda i, j: np.exp(- (i - j) ** 2 / 2.),
shape=(n_dim, n_dim),
)
y = multivariate_normal.rvs(cov=v, size=100)
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
for j in range(y.shape[1]):
ax.scatter(np.full_like(y[:, j], fill_value=j), y[:, j], alpha=0.1, color='red')
for i in range(y.shape[0]):
ax.plot(np.arange(0, n_dim, 1), y[i, :], alpha=0.1, color='red')
ax.set_xlabel('index')
ax.set_ylabel('observed value')
fig.show()

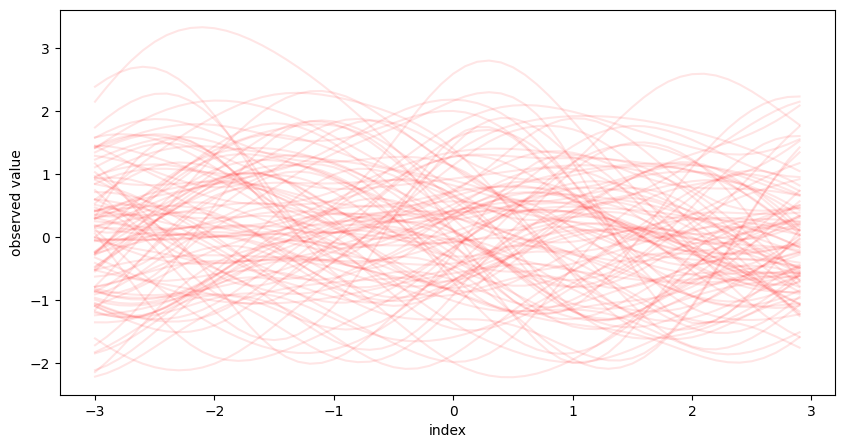
これはパラメータ
なる多変量正規分布 \(\mathrm{N}_{10} ( \mathbf{0}, \Sigma )\) について、標本100個を確率変数の添字 \(i \in \{0, \ldots, 9 \}\) ごとに縦に並べ、対応する標本を (隣接する添字についてのみ) 線で繋いだものです。即ち、各標本はグラフ上の折れ線に対応しています。
なお、これらの共分散行列 \(\Sigma\) の成分 \(\exp \left( - \frac{( i - j )^2}{2} \right)\) は \(i = j\) のとき最大値を取って \(1\) となり、それ以外では \(| i - j |\) が大きくなるほど、即ち2つの添字の値が遠く離れるほど急速に0に近づきます。従って、この \(\Sigma\) をパラメータとする多変量正規分布に従う確率変数のベクトルは添字の値が近い成分ほど相関が大きくなり、また遠く離れるほどほとんど無相関になっていきます。
ガウス過程#
多変量正規分布では確率変数のベクトル \(\mathbf{Y} = ( Y_0, \ldots, Y_{d - 1} )^\mathrm{T}\) を考えていましたが、これを単に添字 \(t \in \{ 0, \ldots, d - 1 \}\) を与えると対応する確率変数 \(Y_t\) が1つ定まるような写像 \(t \mapsto Y_t\) による確率変数の集まり \(Y = \{ Y_t \}_{t \in \{ 0, \ldots, d - 1 \}}\) だと思うことにしましょう(添字の記号は \(i\) や \(j\) から \(t\) に取り替えています)。一般に、このような添字づけられた (indexed) 集まりのことを族 (family) と呼び、確率変数の族のことを 確率過程 (stochastic process) と呼びます。
さて、上記の \(Y\) のように構成した確率変数の族について、その添字 \(t\) が時刻や位置のように \(t = 1.5\) のような非整数や \(t = -3\) のような負数を取るようにして、 \(Y_{1.5}\) や \(Y_{-3}\) のような確率変数を考えることはできるでしょうか? より一般には、添字の集合 \(\mathcal{T} = \{ 0, \ldots, d - 1 \}\) をもっと広いもの、例えば実数 \(\mathbf{R}\) やユークリッド空間 \(\mathbf{R}^k\) に拡張することはできるでしょうか?
実際のところ、これは一定の条件の下で可能です。即ち、ある種の \(\mathcal{T}\) (例えば \(\mathcal{T} = \mathbf{R}\) や \(\mathcal{T} = \mathbf{R}^k\) )に対しては確率変数の族 \(Y = \{ Y_t \}_{t \in \mathcal{T}}\) として(任意のサイズ \(d\) の)任意の有限部分集合 \(\mathcal{T}_d = \{ t_0, \ldots, t_{d - 1} \} \subseteq \mathcal{T}\) が与えられたときに確率変数のベクトル \(Y_{\mathcal{T}_d} = ( Y_{t_0}, \ldots, Y_{t_{d - 1}} )^\mathrm{T}\) が多変量正規分布に従うものを定めることができます。このような確率過程を ガウス過程 (Gaussian process) と呼びます。
適当な条件を満たす関数 \(\mu: \mathcal{T} \to \mathbf{R}\) と \(K: \mathcal{T} \times \mathcal{T} \to \mathbf{R}\) が存在して、上記の \(Y_{\mathcal{T}_d} = ( Y_{t_0}, \ldots, Y_{t_{d - 1}} )^\mathrm{T}\) が従う多変量正規分布が
によって \(\mathrm{N}_d ( \mu_{\mathcal{T}_d}, \Sigma_{\mathcal{T}_d} )\) と書けるものとします。このとき \(Y\) (あるいは \(Y_t\) ) はガウス過程 \(\mathrm{GP} ( \mu, K )\) に従うといい、 \(Y \sim \mathrm{GP} ( \mu, K )\) ( あるいは \(Y_t \sim \mathrm{GP} ( \mu, K )\) ) などと書きます。ガウス過程のパラメータとして、関数 \(\mu\) は 平均関数 と、関数 \(K\) は 共分散関数 や カーネル関数 とそれぞれ呼ばれます。
実際に、 \(\mathcal{T} = \mathbf{R}\) 上のガウス過程を描画してみましょう:
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF
np.random.seed(42)
model = GaussianProcessRegressor(
kernel=RBF(length_scale=1.),
alpha=0.,
)
grid_t = np.arange(-3., 3., 0.1)
sample_paths = model.sample_y(grid_t.reshape(-1, 1), n_samples=100)
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
for i in range(sample_paths.shape[1]):
ax.plot(grid_t, sample_paths[:, i], alpha=0.1, color='red')
ax.set_xlabel('index')
ax.set_ylabel('observed value')
fig.show()
これはパラメータの関数が
なるガウス過程 \(\mathrm{GP} ( \mu, K )\) について、 \(-3 \le t < 3\) の範囲で標本100個を描画したものです。一般に、確率過程 \(\{ Y_t \}_{t \in \mathcal{T}}\) の標本のことを 標本路 (sample path) と呼びます。
個々の標本路 \(y = \{ y_t \}_{t \in \mathcal{T} }\) を考えると、この上で添字 \(t \in \mathcal{T}\) を一つ定めると対応する確率変数の標本 \(y_t \in \mathbf{R}\) が一つ定まります。即ち、ガウス過程の標本路 \(\{ y_t \}_{t \in \mathcal{T} }\)は \(\mathcal{T} \to \mathbf{R}\) なる関数 \(y ( t ) = y_t\) と思うことができ、この意味でガウス過程は \(\mathcal{T}\) 上のランダムな関数の従う確率分布と思うことができるのです。
実際、上記の標本路のグラフも通常の関数のグラフと同様の方法で描画しています。即ち
描画する添字 \(t\) の区間 \([ -3, 3 )\) 上に格子点の集合 \(\mathcal{T}_d = \{ t_0, \ldots, t_{d - 1} \}\) を用意し、
格子点における標本路の値の組 \(y_{\mathcal{T}_d} = ( y_{t_0}, \ldots, y_{t_{d - 1}} )^\mathrm{T}\) を多変量正規分布 \(\mathrm{N}_d ( \mu_{\mathcal{T}_d}, \Sigma_{\mathcal{T}_d} )\) から生成し、
グラフ上で点列 \(( t_0, y_{t_0} ), \ldots, ( t_d, y_{t_d} )\) をこの順に線で繋ぐ
という手順を繰り返すことによって描画しています。詳細は省きますが、このパラメータのガウス過程 \(\mathrm{GP} ( \mu, K )\) についてはこの方法で標本路の関数のよい近似を得ることができます。
正規分布とガウス過程#
つまり、どういうことでしょうか。確率変数が標本空間 \(\Omega\) から実数 \(\mathbf{R}\) への関数だったことを思い出すと見通しがすっきりします。直感的には、標本空間 \(\Omega\) はランダムシードの集合のようなもので、確率変数 \(Y_0 : \Omega \to \mathbf{R}\) はランダムシード \(\omega \in \Omega\) によって実現値が決まる乱数のようなものだと考えて構いません。要点を比較すると
確率変数 \(Y_0\) が正規分布に従う
標本空間の元 \(\omega \in \Omega\) が1つ定まると、実数 \(y = Y_0 ( \omega ) \in \mathbf{R}\) が1つ定まる
確率変数のベクトル \(\mathbf{Y} = ( Y_0, \ldots, Y_{d - 1} )\) が多変量正規分布に従う
標本空間の元 \(\omega \in \Omega\) が1つ定まると、ベクトル \(\mathbf{y} = ( Y_0 ( \omega ), \ldots, Y_{d - 1} ( \omega ) ) \in \mathbf{R}^d\) が1つ定まる
任意の \(\{ i_0, \ldots, i_{d' - 1} \} \subseteq \{ 0, \ldots, d - 1 \}\) について、 \(( Y_{i_0}, \ldots, Y_{i_{d' - 1}} )\) が(多変量)正規分布に従う
確率過程 \(\{ Y_t \}_{t \in \mathcal{T}}\) がガウス過程に従う
標本空間の元 \(\omega \in \Omega\) が1つ定まると、関数 \(y ( \cdot ) = Y_\cdot ( \omega ) \in \mathbf{R}^\mathcal{T}\) が1つ定まる
任意の \(\{ t_0, \ldots, t_{d' - 1} \} \subseteq \mathcal{T}\) について、 \(( Y_{t_0}, \ldots, Y_{t_{d' - 1}} )\) が(多変量)正規分布に従う
となり、ベクトルの確率分布としての多変量正規分布と関数の確率分布としてのガウス過程との類似がよく分かります。
ランダムな関数のモデルにガウス過程を仮定すると、この類似性ゆえに、その関数についての統計的推論を多変量正規分布の統計的推論と同様の方法で行うことができます。しかも通常の回帰分析のように関数の形に具体的な制約を置く必要がありません。次節でその具体的な推論方法を確認してみましょう。
ガウス過程回帰モデル#
機械学習の話題に戻って、標準的な回帰問題を考えます。入出力データ \(\{ ( x_1, y_1 ), \ldots, ( x_n, y_n ) \}\) が与えられて、各 \(i\) に対して入力変数 \(x_i = ( x_{i, 1}, \ldots, x_{i, k} )^{\mathrm{T}} \in \mathbf{R}^k\) かつ出力変数 \(y_i \in \mathbf{R}\) とします。いま、適当な関数 \(f: \mathbf{R}^k \to \mathbf{R}\) を用いた回帰モデル
を考えて、各 \(\epsilon_i \sim \mathrm{N} ( 0, \sigma_\epsilon^2 )\) は独立同分布な雑音とします。 ガウス過程回帰 (Gaussian process regression ; GPR) モデルでは、この関数 \(f\) が \(\mathbf{R}^k\) 上のガウス過程に従うランダムな関数だと仮定して推論を行います。
ガウス過程回帰モデルを用いた予測#
関数 \(f\) がガウス過程 \(\mathrm{GP} ( \mu, K )\) に従うものとします。ここでは平均関数 \(\mu: \mathbf{R}^k \to \mathbf{R}\) かつカーネル関数 \(K: \mathbf{R}^k \times \mathbf{R}^k \to \mathbf{R}\) とします。このとき
として
とおきます。ただし、 \(\mu ( X )\) と \(K ( X, X )\) については各関数の値を並べたベクトルや行列に記号を流用しました。このとき、関数 \(f\) の出力を並べたベクトル \(\mathbf{f}\) は多変量正規分布 \(\mathrm{N}_n ( \mu ( X ), K ( X, X ) )\) に従います。また、雑音を並べたベクトル \(\boldsymbol{\epsilon}\) は ( \(\mathbf{f}\) とは独立に) \(\mathrm{N}_n ( \mathbf{0}, \sigma_\epsilon^2 I_n )\) に従うので、出力変数を並べたベクトル \(\mathbf{y} = \mathbf{f} + \boldsymbol{\epsilon}\) は \(\mathrm{N}_n ( \mu ( X ), K ( X, X ) + \sigma_\epsilon^2 I_n )\) に従います。
この下で、新しい入力 \(x_{n + 1}, \ldots, x_{n + m} \in \mathbf{R}^k\) に対する出力を予測したいものとします。このとき
として
とおきます。やはり \(\mu ( X_* )\) や \(K ( X, X_* )\) などについては記号を流用しました。いま \(f \sim \mathrm{GP} ( \mu, K )\) と仮定していたので \(\mathbf{f}\) と \(\mathbf{f}_*\) の同時分布は多変量正規分布となります。従って \(\mathbf{y} = \mathbf{f} + \boldsymbol{\epsilon}\) と \(\mathbf{f}_*\) の同時分布も多変量正規分布となって
と表せます。
データ \(\{ ( x_1, y_1 ), \ldots, ( x_n, y_n ) \}\) が与えられた下で新しい入力 \(x_{n + 1}, \ldots, x_{n + m}\) に対する出力を予測するには、上記の同時分布から \(\mathbf{f}_* | \mathbf{y}\) の条件付き分布を導けば十分です。導出の詳細は省きますが、この条件付き分布も多変量正規分布となって
と表せます。ただし
とします。なお、雑音も考慮して
とおいて \(\mathbf{y}_* = \mathbf{f}_* + \boldsymbol{\epsilon}_*\) の条件付き分布を考えたい場合は、単に
となります。後はこれら \(\mathbf{y}_*\) や \(\mathbf{f}_*\) の条件付き分布を使って予測の点推定や区間推定を行うことができます。
Scikit-learnにおけるガウス過程回帰モデル#
ガウス過程回帰モデルを実装しているPythonライブラリとしてはscikit-learnやGPyが有名です。また、TensorFlowベースのGPflowやPyTorchベースのGPyTorchも近年はよく使われています。本節では、このうちscikit-learn ( sklearn ) を用いたガウス過程回帰の実行について簡単に解説します。
利用する訓練データ \(D = \{ ( x_1, y_1 ), \ldots, ( x_{10}, y_{10} ) \}\) を次のように構成します。入力変数 \(x_i \in \mathbf{R} \; ( i = 1, \ldots, 10 )\) を一様分布 \(\mathrm{U} ( -10, 10 )\) から独立に生成し、対応する出力変数 \(x_i \in \mathbf{R}\) を
によって生成します。ただし、各 \(n_i \in \mathbf{R}\) は正規分布 \(\mathrm{N} ( 0, ( 0.25 )^2 )\) から独立に生成するものとします。
def f(x):
return np.sin(0.3 * x)
np.random.seed(42)
x_train = np.random.uniform(-10., 10., size=(10, 1))
eps_train = np.random.normal(0., 0.25, size=(10, 1))
y_train = f(x_train) + eps_train
x_test = np.arange(-10., 10., 0.1).reshape(-1, 1)
y_true = f(x_test)
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
ax.scatter(x_train, y_train, label='train', color='C0')
ax.plot(x_test, y_true, label='true f', color='C1')
ax.set_xlim(-10., 10.)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.legend(loc=2)
fig.show()

このデータ \(D\) に対して、ガウス過程回帰モデル
による推論を行います。ここで関数 \(f\) はガウス過程 \(\mathrm{GP} ( \mu, K )\) に従うものとし、その平均関数 \(\mu\) とカーネル関数 \(K\) はそれぞれ
で定めます。ただし \(C > 0\) と \(\ell > 0\) はカーネル関数のパラメータです。また、誤差項 \(\epsilon_i\) は独立に正規分布 \(\mathrm{N} ( 0, \sigma_\epsilon^2 )\) に従うものとします。
カーネルのパラメータ \(C, \ell\) や誤差項のパラメータ \(\sigma_\epsilon^2\) の取り扱いはデータに応じて適切に決定しないといけません。今回利用するscikit-learnの GaussianProcessRegressor では、特に指定しなければ訓練データの対数周辺尤度を最大化するようにこれらのパラメータの値が決定されます(詳細は後述)。
# from sklearn.gaussian_process import GaussianProcessRegressor
# from sklearn.gaussian_process.kernels import RBF
from sklearn.gaussian_process.kernels import ConstantKernel, WhiteKernel
regr = GaussianProcessRegressor(
kernel=ConstantKernel() * RBF() + WhiteKernel(), # カーネルの演算については後述
alpha=0., # 雑音項はカーネルの中で表現しているので 0. を指定
# optimizer=None,
)
regr.fit(x_train, y_train)
regr.kernel_ # 推定されたカーネルと誤差項のパラメータを確認
0.774**2 * RBF(length_scale=5.43) + WhiteKernel(noise_level=0.0384)
では、実際にガウス過程回帰モデルによる関数の予測を描画してみましょう。 GaussianProcessRegressor.predict() メソッドに新しい入力 \(X_*\) を渡すと、対応する予測分布 \(\mathbf{y}_* | \mathbf{y}\) の平均 \(\mu_{* | \mathbf{y}}\) を返してくれます。また、併せて引数 return_std=True を渡すと、 \(\mathbf{y}_* | \mathbf{y}\) の各成分の予測標準偏差を並べたベクトル
を返してくれます。ただし、ここで \(\mathrm{diag} ( \cdot )\) は行列の対角成分を並べたベクトルを返すものとし、平方根はベクトルの成分毎に取るものとします。
y_pred, y_std = regr.predict(x_test, return_std=True) # y*の平均と標準偏差を計算
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
ax.scatter(x_train, y_train, label='train', color='C0')
ax.plot(x_test, y_true, label='true f', color='C1')
ax.plot(x_test, y_pred, label='pred. mean', color='red') # y*の平均関数を描画
ax.fill_between(
x_test.flatten(),
y_pred.flatten() - 3. * y_std.flatten(),
y_pred.flatten() + 3. * y_std.flatten(),
label='pred. intvl.', color='red', alpha=0.3,
) # y*の3-sigma予測区間を描画
ax.set_xlim(-10., 10.)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.legend(loc=2)
fig.show()

図の赤線がガウス過程回帰モデルの計算した各点での予測平均を繋いだもの、薄い赤色の領域が同じく各点での予測3σ-区間を繋いだものです。データの多い領域では予測区間の幅が小さくなり、逆にデータの少ない領域では幅が広くなっていることが分かります。
ガウス過程回帰モデルの計算量#
以上のように、ガウス過程回帰は入出力の訓練データ \(( X, \mathbf{y} )\) さえあれば未知の入力 \(X_*\) に対する予測を行うことができ、しかも予測分布という形でその不確実性まで評価できる極めて強力なモデルとなっています。ただし、その代償としてガウス過程回帰の計算量は時間的にも空間的にも非常に大きいものとなっています。
簡単のため、予測に用いる条件付き分布 \(\mathbf{f}_* | \mathbf{y}\) や \(\mathbf{y}_* | \mathbf{y}\) の平均
のみ計算する場合を考えましょう。式中のベクトルや行列のサイズはそれぞれ
でした。複数回の予測を行うことを前提に、訓練データが与えられた時点で
なるベクトル \(\alpha \in \mathbf{R}^n\) の値を予め計算しておき、新しい入力 \(X_*\) が与えられるごとに
によって予測を行うことにします。このとき、ナイーブなアルゴリズムでは \(\alpha\) を求める部分で \(O ( n^3 )\) の、行列積 \(K ( X, X_* )^\mathrm{T} \alpha\) を求める部分で \(O ( m n )\) の時間計算量になりますから、この式全体では \(O ( m n + n^3 )\) の計算量になります。
では、例えば訓練データの数 \(n\) が10倍になったとすると、予測の平均 \(\mu_{* | \mathbf{y}}\) の計算に必要な時間は何倍になるでしょうか? 訓練データから \(\alpha\) を求める部分については \((10 n)^3 = 1000 n^3\) ですから、(ある程度 \(n\) が大きいと)1000倍程度の時間になることが予想されます。新しい入力 \(X_*\) に対して \(K ( X, X_* )^\mathrm{T} \alpha\) を計算する部分については \(m (10 n) = 10 m n\) ですから、(ある程度 \(n\) が大きいと、また \(m\) が同じなら)およそ10倍程度の時間になることが予想されます。
実際にscikit-learnのアルゴリズムでそれぞれの実行時間を計測してみましょう。
import time
def test_gpr_time(n, m):
x = np.random.uniform(-10., 10., size=(n, 1))
eps = np.random.normal(0., 0.25, size=(n, 1))
y = f(x) + eps
x_new = np.random.uniform(-10., 10., size=(m, 1))
param_const = 0.75 ** 2
param_rbf_ls = 5.5
param_white_nl = 0.04
kernel = param_const * RBF(length_scale=param_rbf_ls) + WhiteKernel(noise_level=param_white_nl)
regr = GaussianProcessRegressor(
kernel=kernel, # 上の例で求めたのと近い値を予め代入したカーネルを利用
alpha=0., # このalphaは雑音項であることに注意;今回もカーネルに含んでいるので0
optimizer=None, # 対数周辺尤度の最大化を行わず、所与のハイパーパラメータを利用
)
train_start = time.perf_counter()
regr.fit(x, y) # Scikit-learnでもここでCholesky分解を行って上式のα (regr.alpha_) を求めている
train_stop = time.perf_counter()
pred_start = time.perf_counter()
y_new_hat = regr.predict(x_new) # 今回は平均のみ求める
pred_stop = time.perf_counter()
return train_stop - train_start, pred_stop - pred_start
n1 = 500
t1_train, t1_pred = test_gpr_time(n1, 5)
print(f'Time for n={n1}: {t1_train}(s) for training, and {t1_pred} (s) for prediction.')
n2 = 10 * n1
t2_train, t2_pred = test_gpr_time(n2, 5)
print(f'Time for n={n2}: {t2_train}(s) for training, and {t2_pred} (s) for prediction.')
print(f'Rate: {t2_train / t1_train} for training, and {t2_pred / t1_pred} for prediction.')
Time for n=500: 0.015469598999999334(s) for training, and 0.0010216049999982602 (s) for prediction.
Time for n=5000: 3.2227119060000007(s) for training, and 0.014965555999999935 (s) for prediction.
Rate: 208.32549738361928 for training, and 14.649062994039205 for prediction.
実際の時間は実行環境に依存しますが、この程度の \(n\) だとまだ支配的な項(訓練の \(n^3\) や予測の \(m n\) )以外の影響も強いため1000倍、ないし10倍近くまでは行かないことが多いと思われます。
一方、空間計算量についても無視できません。詳細は省きますが、ナイーブなアルゴリズムでは \(\mu_{* | \mathbf{y}}\) を求めるのに \(O ( m n + n^2 )\) の空間計算量がかかります。このため、同じく訓練データ数 \(n\) が10倍になると予測には100倍程度のメモリーが必要になります。実際にこれらのサイズの行列の積を計算する必要があるため、深層学習でよく使われるようなミニバッチ戦略による空間計算量の削減も直接適用できません。
これらの時間的・空間的な計算量の問題により、データ数 \(n\) が大きい場合にガウス過程回帰モデルを利用するには、カーネル行列を低ランク近似する (Silverman, 1985) 、変分推論を行う (Titsias, 2009) などの工夫が必要になります。これらの手法については(scikit-learnに実装されていないこともあり)解説を別項に譲り、本稿では割愛します。
基本的なカーネル関数とその演算#
本節ではガウス過程回帰モデルで利用される基本的なカーネル関数について解説した後、それらのカーネルを合成して所望の性質を持つ関数を生成させる方法、およびカーネル関数のパラメータを最適化する方法について触れます。
基本的なカーネル関数#
ここでは入力変数 \(x\) がユークリッド空間 \(\mathbf{R}^k\) に属するときに使われる主要なカーネル関数について、その表式と特徴について簡単に解説した後、そのカーネル関数をパラメータとするガウス過程から生成した標本路を描画していきます。
なお、以下においては断りのない限り \(\| \cdot \|\) でユークリッドノルム (l2ノルム) を表すものとします。
RBFカーネル#
これまで主に利用してきた
の形のカーネル関数をRBFカーネル (radial basis function kernel; 動径基底関数カーネル) と呼びます。この名称はこの形の関数が動径基底関数としてよく使われることに由来するもので、ほかにも二乗指数カーネル (squared exponetial kernel) 、指数二次カーネル (exponentiated quadratic kernel) 、ガウシアンカーネル (Gaussian kernel) などの呼び方があります。パラメータ \(\ell > 0\) は長さスケール (length scale) と呼ばれ、この \(\ell\) が大きいほど関数の値が相関する距離が長くなります。
# from sklearn.gaussian_process.kernels import RBF
np.random.seed(42)
model = GaussianProcessRegressor(
kernel=RBF(length_scale=1.),
alpha=0.,
)
grid_t = np.arange(-3., 3., 0.1)
sample_paths = model.sample_y(grid_t.reshape(-1, 1), n_samples=20)
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
for i in range(sample_paths.shape[1]):
ax.plot(grid_t, sample_paths[:, i], alpha=0.2, color='red')
ax.set_title('Samples with an RBF kernel')
ax.set_xlabel('index')
ax.set_ylabel('observed value')
fig.show()

Matérnカーネル#
RBFカーネル以外でよく使われるカーネルに Matérnクラス のカーネル関数があります。Matérnクラスのカーネル関数は添字 \(\nu > 0\) を持つ関数の族で、特に \(\nu = 3 / 2\) のときの
(しばしば Matérn 3/2 カーネル とも)および \(\nu = 5/2\) のときの
(しばしば Matérn 5/2 カーネル とも)がガウス過程のカーネル関数としてはよく使われます。いずれのパラメータ \(\ell > 0\) もやはり長さスケールと呼ばれます。
Matérnクラスのカーネル関数はRBFカーネルよりも滑らかでない関数を生成したいときによく使われます。同じ長さスケール \(\ell\) でも添字 \(\nu\) が小さいほど狭い範囲でぐねぐねとした関数を生成しやすくなり、関数の値の局所的な小さい変化にも対応できます。また、 \(\nu \to \infty\) の極限においてMatérnカーネルはRBFカーネルに一致します。
from sklearn.gaussian_process.kernels import Matern
np.random.seed(42)
model = GaussianProcessRegressor(
kernel=Matern(length_scale=1., nu=1.5),
alpha=0.,
)
grid_t = np.arange(-3., 3., 0.1)
sample_paths = model.sample_y(grid_t.reshape(-1, 1), n_samples=20)
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
for i in range(sample_paths.shape[1]):
ax.plot(grid_t, sample_paths[:, i], alpha=0.2, color='red')
ax.set_title('Samples with a Matern 3/2 kernel')
ax.set_xlabel('index')
ax.set_ylabel('observed value')
fig.show()

# from sklearn.gaussian_process.kernels import Matern
np.random.seed(42)
model = GaussianProcessRegressor(
kernel=Matern(length_scale=1., nu=2.5),
alpha=0.,
)
grid_t = np.arange(-3., 3., 0.1)
sample_paths = model.sample_y(grid_t.reshape(-1, 1), n_samples=20)
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
for i in range(sample_paths.shape[1]):
ax.plot(grid_t, sample_paths[:, i], alpha=0.2, color='red')
ax.set_title('Samples with a Matern 5/2 kernel')
ax.set_xlabel('index')
ax.set_ylabel('observed value')
fig.show()

Exponentiated Sine Squaredカーネル#
特に \(x \in \mathbf{R}\) のとき、
の形のカーネルを、 exponeniated sine squared kernel や、単に周期的カーネル (periodic kernel) と呼びます。パラメータ \(\ell > 0\) は長さスケール、 \(p > 0\) は周期と呼ばれます。実際、半角公式より
となり、この関数は \(\| x - x' \|\) について基本周期 \(p\) の周期関数になっていることが分かります。
このカーネル関数をパラメータとするガウス過程において、2点 \(x, x + p \in \mathbf{R}\) における関数の値を \(f_x, f_{x + p}\) とすると
および、同様に \(V ( f_x ) = V ( f_{x + p} ) = 1\) より相関係数 \(\rho_{f_x, f_{x + p}} = 1\) となります。即ちこのカーネル関数をパラメータとするガウス過程に従う関数も確率1で基本周期 \(p\) の周期関数になっています。
from sklearn.gaussian_process.kernels import ExpSineSquared
np.random.seed(42)
model = GaussianProcessRegressor(
kernel=ExpSineSquared(length_scale=1.0, periodicity=2.0),
alpha=0.,
)
grid_t = np.arange(-3., 3., 0.1)
sample_paths = model.sample_y(grid_t.reshape(-1, 1), n_samples=20)
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
for i in range(sample_paths.shape[1]):
ax.plot(grid_t, sample_paths[:, i], alpha=0.2, color='red')
ax.set_title('Samples with an exp-sine-squared kernel')
ax.set_xlabel('index')
ax.set_ylabel('observed value')
fig.show()

点乗積カーネル#
次の形のカーネル関数
を 点乗積カーネル (dot product kernel) または 線形カーネル (linear kernel) と呼びます。なお、定義によっては \(\sigma_0^2\) の項を含まない場合があります。
このカーネル関数をパラメータとするガウス過程回帰を行うことは、通常のベイズ線型回帰を行うことと等価になります。即ち、このカーネル関数をパラメータとするガウス過程に従う関数は確率1で直線となります。ガウス過程回帰においてこのカーネル関数を単独で用いることはほとんどなく、後述のように他のカーネルと組み合わせて線形のトレンドや異分散性を表現するために利用されることがほとんどです。
from sklearn.gaussian_process.kernels import DotProduct
np.random.seed(42)
model = GaussianProcessRegressor(
kernel=DotProduct(sigma_0=1.0),
alpha=0.,
)
grid_t = np.arange(-3., 3., 0.1)
sample_paths = model.sample_y(grid_t.reshape(-1, 1), n_samples=20)
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
for i in range(sample_paths.shape[1]):
ax.plot(grid_t, sample_paths[:, i], alpha=0.2, color='red')
ax.set_title('Samples with a dot-product kernel')
ax.set_xlabel('index')
ax.set_ylabel('observed value')
fig.show()

白色雑音カーネル#
次の形のカーネル関数
を 白色雑音カーネル (white noise kernel) または 白色カーネル (white kernel) と呼びます。なお、ここで \(1_A\) は論理式 \(A\) が成り立つときに1を、そうでないときに0を取る写像とします。
このカーネル関数をパラメータとするガウス過程では任意の異なる \(x, x'\) に対して \(K_\mathrm{WN} ( x, x' ) = 0\) となるため、白色雑音が生成されます。このカーネル関数を単独で用いることはほぼなく、専ら後述のように他のカーネル関数と組み合わせることでガウス過程回帰モデル
の雑音項 \(\epsilon_i\) の効果をカーネルの一部として処理するために使われます。
from sklearn.gaussian_process.kernels import WhiteKernel
np.random.seed(42)
model = GaussianProcessRegressor(
kernel=WhiteKernel(noise_level=1.0),
alpha=0.,
)
grid_t = np.arange(-3., 3., 0.1)
sample_paths = model.sample_y(grid_t.reshape(-1, 1), n_samples=20)
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
for i in range(sample_paths.shape[1]):
ax.plot(grid_t, sample_paths[:, i], alpha=0.2, color='red')
ax.set_title('Samples with a white noise kernel')
ax.set_xlabel('index')
ax.set_ylabel('observed value')
fig.show()

カーネルの組み合わせ#
カーネル関数の演算#
これらのカーネル関数を組み合わせて用いることで、より込み入った性質の標本路を生成するガウス過程を考えることができます。いま、2つのカーネル関数 \(K_1\), \(K_2\) の和と積、および定数 \(c > 0\) による定数倍をそれぞれ
のように定義します。
実際に、周期的カーネルと線形カーネルを組み合わせたカーネルがどのような標本路を生成するのか確認してみましょう。最初に周期的カーネルと線形カーネルの和の場合、以下のように線形なトレンドと周期成分の和に分解できるような標本路が生成されます。
np.random.seed(42)
kernel = DotProduct(sigma_0=1.0) + ExpSineSquared(length_scale=1.0, periodicity=2.0)
model = GaussianProcessRegressor(
kernel=kernel,
alpha=0.,
)
grid_t = np.arange(0., 6., 0.1)
sample_paths = model.sample_y(grid_t.reshape(-1, 1), n_samples=20)
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
for i in range(sample_paths.shape[1]):
ax.plot(grid_t, sample_paths[:, i], alpha=0.2, color='red')
ax.set_title('Samples with an additive kernel')
ax.set_xlabel('index')
ax.set_ylabel('observed value')
fig.show()

次に周期的カーネルと線形カーネルの積の場合、以下のように周期成分の振幅が線形に拡大していくような標本路が生成されます。
np.random.seed(42)
kernel = DotProduct(sigma_0=1.0) * ExpSineSquared(length_scale=1.0, periodicity=2.0)
model = GaussianProcessRegressor(
kernel=kernel,
alpha=0.,
)
grid_t = np.arange(0., 6., 0.1)
sample_paths = model.sample_y(grid_t.reshape(-1, 1), n_samples=20)
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
for i in range(sample_paths.shape[1]):
ax.plot(grid_t, sample_paths[:, i], alpha=0.2, color='red')
ax.set_title('Samples with a productive kernel')
ax.set_xlabel('index')
ax.set_ylabel('observed value')
fig.show()

最後に周期的カーネルの定数倍の場合、単純に振幅の拡大または縮小された周期的な標本路が生成されます。
# from sklearn.gaussian_process.kernels import ConstantKernel
np.random.seed(42)
kernel = ConstantKernel(constant_value=2.0 ** 2) * ExpSineSquared(length_scale=1.0, periodicity=2.0)
model = GaussianProcessRegressor(
kernel=kernel,
alpha=0.,
)
grid_t = np.arange(0., 6., 0.1)
sample_paths = model.sample_y(grid_t.reshape(-1, 1), n_samples=20)
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
for i in range(sample_paths.shape[1]):
ax.plot(grid_t, sample_paths[:, i], alpha=0.2, color='red')
ax.set_title('Samples with a scalar-multiplicated kernel')
ax.set_xlabel('index')
ax.set_ylabel('observed value')
fig.show()
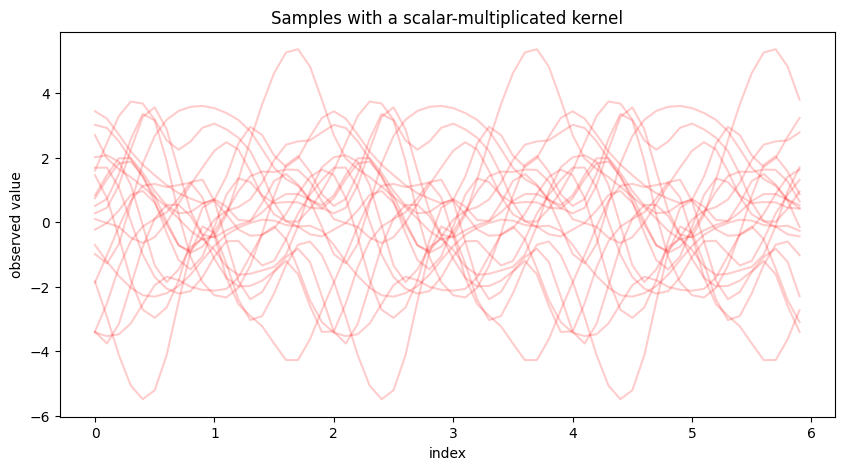
では、ここで次のようなカーネル関数
を考えてみましょう。ただし \(\sigma_\mathrm{Lin}^2\), \(\sigma_\mathrm{Per}^2\), \(\sigma_\mathrm{M32}^2\) はそれぞれ正の定数とします。このカーネル関数を用いたガウス過程はどのような標本路を生成するでしょうか?
np.random.seed(42)
kernel = ConstantKernel(constant_value=1.0) * DotProduct(sigma_0=0.) + \
ConstantKernel(constant_value=1.0) * ExpSineSquared(length_scale=1.0, periodicity=2.0) + \
ConstantKernel(constant_value=1.0) * Matern(length_scale=1.0, nu=1.5)
model = GaussianProcessRegressor(
kernel=kernel,
alpha=0.,
)
grid_t = np.arange(0., 6., 0.1)
sample_paths = model.sample_y(grid_t.reshape(-1, 1), n_samples=20)
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
for i in range(sample_paths.shape[1]):
ax.plot(grid_t, sample_paths[:, i], alpha=0.2, color='red')
ax.set_title('Samples with a composite kernel')
ax.set_xlabel('index')
ax.set_ylabel('observed value')
fig.show()
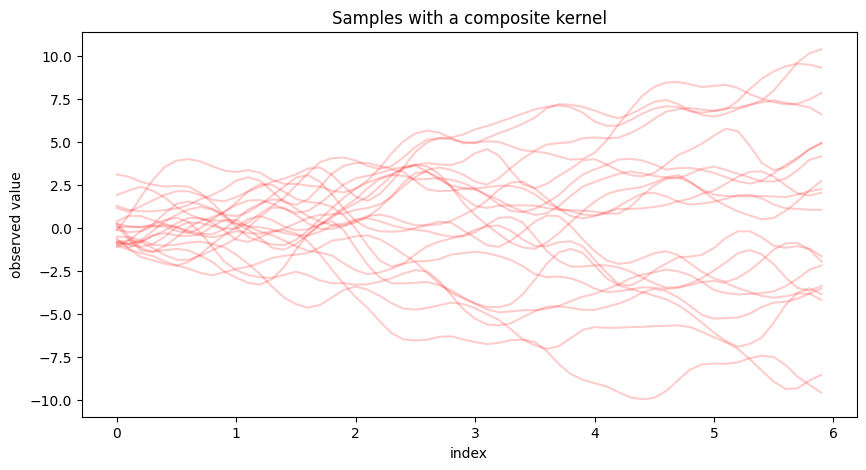
上図のように、カーネル関数 \(K\) を用いたガウス過程が生成する標本路は
線形カーネルに由来する線形のトレンド成分
周期的カーネルに由来する周期的な成分
Matérn 3/2 カーネルに由来する局所的に相関した成分
の3つの和に分解できるものとなります。経済時系列の解析でトレンドや季節性を考慮したモデリングをしているのと近いですが、ガウス過程ではそれらがすべてカーネル関数という単一の形式で表現できていること、また添字 \(x\) が等間隔に並んだ時刻以外の場合でも容易に推論を実行できることなどに注意が必要です。
白色雑音カーネルとの合成#
訓練データの入力 \(x_1, \ldots, x_n\) が相異なるとき、白色雑音カーネル \(K_\mathrm{WN}\) について
となります。また、新しい入力 \(x_{n + 1}, \ldots, x_{n + m}\) が相異なり、しかも訓練データのいずれとも相異なるとき、同様に
となります。
いま、元のカーネル \(K\) と白色雑音カーネル \(K_\mathrm{WN}\) を加えた \(K' = K + K_\mathrm{WN}\) をカーネル関数とするガウス過程 \(\mathrm{GP} ( \mu, K' )\) を考え、関数 \(f \sim \mathrm{GP} (\mu, K' )\) の訓練データ \(X\) と新しいデータ \(x_*\) に対する出力を並べたベクトルをそれぞれ \(\mathbf{f}, \mathbf{f}_*\) とおくと、以上の結果より
となります。これは上記のガウス過程回帰モデルにおける出力変数 \(\mathbf{y}, \mathbf{y}_*\) の同時分布と同じ形になっています。この性質より、ガウス過程回帰モデルの推論において雑音項を明示的に扱う代わりに白色雑音カーネルを利用することがよく行われます。
Scikit-learnのガウス過程回帰モデルにおいては、デフォルトの設定だと雑音の分散 \(\sigma_\epsilon^2\) が既知のもの(デフォルト値では \(\sigma_\epsilon^2 = 10^{- 10}\) )として推論が行われます。この分散の値もデータから推定する場合は、 GaussianProcessRegressor に渡すカーネルに明示的に白色雑音カーネルを加えた上で、この分散に対応する引数 alpha を形式的に0に設定する必要があります。実際、前出の「Scikit-learnにおけるガウス過程回帰モデル」節の例ではそのように実装していました。
同じデータで、雑音の分散を推定せずにデフォルトの取り扱いをする場合のコードと推定結果のグラフは次のようになります。
regr_kv = GaussianProcessRegressor(
kernel=ConstantKernel() * RBF(), # 白色雑音カーネルの項を省く
# alpha=1e-10, # 雑音の分散にデフォルトの値を利用
# optimizer=None,
)
regr_kv.fit(x_train, y_train)
regr_kv.kernel_ # 推定されたカーネルと誤差項のパラメータを確認
0.827**2 * RBF(length_scale=1e-05)
y_pred_kv, y_std_kv = regr_kv.predict(x_test, return_std=True) # f*の平均と標準偏差を計算
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
ax.scatter(x_train, y_train, label='train', color='C0')
ax.plot(x_test, y_true, label='true f', color='C1')
ax.plot(x_test, y_pred_kv, label='pred. mean', color='red') # f*の平均関数を描画
ax.fill_between(
x_test.flatten(),
y_pred_kv.flatten() - 3. * y_std_kv.flatten(),
y_pred_kv.flatten() + 3. * y_std_kv.flatten(),
label='pred. intvl.', color='red', alpha=0.3,
) # f*の3-sigma予測区間を描画
ax.set_xlim(-10., 10.)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.legend(loc=2)
fig.show()
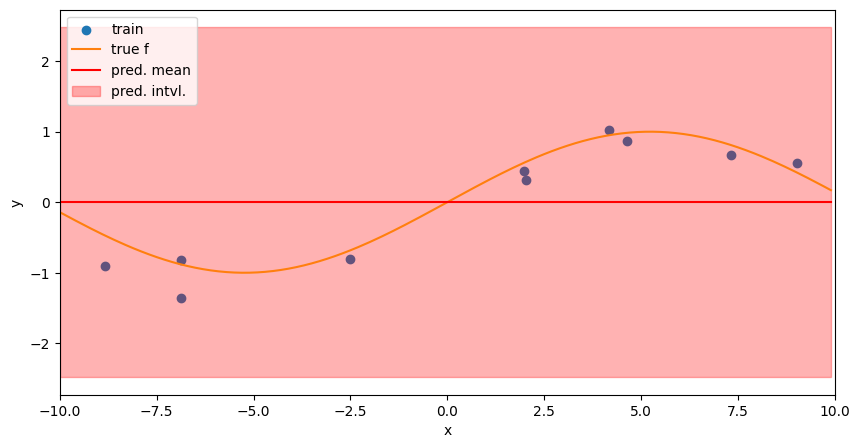
一見して目的関数が適切に推定されていないことがわかります。
カーネルのハイパーパラメータの最適化#
これまでトイデータの解析に利用してきたカーネル
にはハイパーパラメータ \(\eta = ( C, \ell )\) (雑音項の分も含めるなら \(\eta = ( C, \ell, \sigma_\epsilon^2 )\) ) が存在しますが、先述の通りscikit-learnではこれを対数周辺尤度の最大化により推定しています。この最適化について簡単に説明します。
ベイズ推論において、データの尤度を事前分布で周辺化した値、ガウス過程回帰の場合は
をデータの 周辺尤度 (marginal likelihood) または エビデンス と呼びます。この値は事前分布 \(p ( \mathbf{f} | \eta )\) (ここではガウス過程の導く多変量正規分布) とモデル \(p ( \mathbf{y} | \mathbf{f} )\) (ここでは加法ノイズ) の組がどれほどデータ \(\mathbf{y}\) を表すのに相応しいかを示す量と思うことができます。この周辺尤度を最大化するように事前分布のハイパーパラメータ \(\eta\) を推定することは経験ベイズ (empirical Bayes) 法やエビデンス近似、あるいは第二種の最尤推定と呼ばれます。
通常のガウス過程回帰において、データの(対数)周辺尤度は解析的に計算できて
となります。これをハイパーパラメータ \(\eta\) の関数と思った際の勾配も容易に求まるため、一般的な最適化手法を用いて(局所的に)最大化することが可能です。
# log_marginal_likelihood() メソッドで訓練データについての対数周辺尤度を計算できる
# 雑音の分散をカーネルの一部として推定したモデル
print(f'Log marginal likelihood (estimated variance): {regr.log_marginal_likelihood()}.')
# 雑音の分散を既知としてデフォルトの値を与えたモデル
print(f'Log marginal likelihood (given variance): {regr_kv.log_marginal_likelihood()}.')
Log marginal likelihood (estimated variance): -4.607462036460479.
Log marginal likelihood (given variance): -12.290747019995884.
小括#
本稿ではガウス過程について多変量正規分布とのアナロジーから直感的な描写を試みた上で、ガウス過程回帰モデルの基本とそのscikit-learnにおける実装、またガウス過程で用いられるカーネル関数の取り扱いについて簡単に解説しました。ガウス過程回帰モデルではデータサイズに依存する計算量と引き換えに柔軟な推論を行うことができるため、特にデータ数がそれほど多くない場合には高い性能を発揮します。
ガウス過程の応用は回帰問題に限らず、ガウス過程潜在変数モデル (GPLVM) という枠組みを通じて分類問題やより複雑な階層的モデリングも行うことができます。また、データ数が多い場合でも変分近似を行うことによって現実的な時間で推論を実行することができます。これらの発展的な話題については後に別項で解説する予定です。
参考文献#
教科書
Rasmussen, C. E. and Williams C. K. I. (2006). Gaussian Processes for Machine Learning. The MIT Press.
機械学習でガウス過程を利用する際の標準的な教科書の一つ。
電子版 (PDFファイル) は公式サイトから無料でダウンロードできます。
Webサイト
Gaussian Processes: https://scikit-learn.org/stable/modules/gaussian_process.html
ガウス過程についてのscikit-learnのユーザガイド。
Kernel Cookbook: https://www.cs.toronto.edu/~duvenaud/cookbook/
ガウス過程のカーネル関数の構成について解説したページ。
本稿では省いた多変量のカーネルの構成についての解説もあり。
学術論文など
Silverman, B. W. (1985). Some aspects of the spline smoothing approach to non‐parametric regression curve fitting. Journal of the Royal Statistical Society: Series B (Methodological), 47 (1), 1-21.
Titsias, M. (2009). Variational learning of inducing variables in sparse Gaussian processes. Proceedings of the Twelth International Conference on Artificial Intelligence and Statistics, PMLR 5, 567-574.

