密度推定による異常検知の基礎#
本稿では異常検知の基礎的な手法のうち、確率密度の推定によるものを解説します。即ち、
という一連の流れをモデルが正規分布の場合について説明し、あわせて異常の原因を説明する手法の一つとしてMahalabois-Taguchi法(MT法) を紹介します。
序論#
本節では統計・機械学習を用いた異常検知の考え方について簡単に説明し、あわせて本稿で利用するデータの概略を描写します。
統計・機械学習と異常検知#
異常検知 (anomaly detection) の問題設定として最も一般的なのは、未知の新しいデータを得たときにそれが何らかの基準に照らして正常であるか異常であるかを決定したい、というものでしょう。この決定則について、古典的には知識や経験則を人間の専門家がIF-THENルールなどの決定木の形で表現することがよく行われていました。一方、近年は既知のデータから統計・機械学習の手法によって決定則のパラメータを導出することも多くなっています。こうしたデータにもとづく異常検知の手続きを抽象的にまとめると、次のような3段階
正常なデータのモデリング
異常度の定義
閾値の設定
に分けることができます。即ち、正常なデータが従うモデルを学習し、このモデルをもとにして新しいデータの異常度を計算する関数を作成し、新しいデータの異常度が一定の値を超えた場合に異常と判定する、その閾値を設定する、というスキームで表現できることがほとんどです。
このうち最初の段階の正常なデータのモデリングとしては、扱うデータの種類に応じて
密度推定によるもの
次元削減によるもの
回帰モデル(時系列回帰なども含む)によるもの
などがよく用いられます。密度推定は特に入出力関係などがなく不要な特徴も少ないデータ、次元削減は不要な特徴や強く関連する特徴が存在するデータ、回帰モデルは入出力関係があったり時系列性のあるデータの場合に利用されるものです。
本稿では、このうち密度推定による異常検知の基礎的な方法を取り扱います。次元削減や回帰モデルによる異常検知、あるいは密度推定による異常検知の発展的な内容についてはそれぞれ対応する記事をご参照ください。
データ#
本稿ではscikit-learnのirisデータセットを利用します。これは3種類のアヤメ (setosa, versicolor, virginica) の花について萼の長さと幅、また花弁の長さと幅を記録したもので、分類問題の初歩的なアルゴリズムを開設する際によく用いられるものです。
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
%matplotlib inline
from sklearn.datasets import load_iris
d = load_iris()
d['feature_names'] # 各特徴の名称(4種類)
['sepal length (cm)',
'sepal width (cm)',
'petal length (cm)',
'petal width (cm)']
d['target_names'] # 各クラスの名称(3種類)
array(['setosa', 'versicolor', 'virginica'], dtype='<U10')
x0 = d['data'][d['target'] == 0, :].copy() # クラス0 (setosa) の標本の特徴を x0 に格納
x1 = d['data'][d['target'] == 1, :].copy() # クラス1 (versicolor) の標本の特徴を x1 に格納
x2 = d['data'][d['target'] == 2, :].copy() # クラス2 (virginica) の標本の特徴を x2 格納
print(f'Shape of x0: {x0.shape}.')
print(f'Shape of x1: {x1.shape}.')
print(f'Shape of x2: {x2.shape}.')
Shape of x0: (50, 4).
Shape of x1: (50, 4).
Shape of x2: (50, 4).
一変量正規分布に従うデータにおける異常検知#
本節では、確率密度の推定にもとづく異常検知について概説した後、一変量正規分布に従うと考えられるデータの異常検知の方法、特にHotelling理論と呼ばれる方法について要点を解説します。
密度推定による異常検知#
異常 (anomaly) の定義はさまざまに考えられますが、普通には見られないこと、めったにはあり得ないことを異常と見なすのは一つの自然な見方です。これを数学的な概念に落とし込んでいくと、新しいデータ \(x'\) が異常であるかどうかはそのデータ(に近いデータ)が得られる確率が十分小さいかどうかで判定できそうだ、ということになります。このような異常検知のプロセスを実現するには
何らかの方法で正常なデータが従うと考えられる確率モデルを構成し、
そのモデルから計算される確率(連続データなら確率密度)を基に何らかの異常度 \(a ( \cdot )\) を定義し、
新しいデータ \(x'\) の異常度 \(a ( x' )\) が正常か異常かを分ける閾値を設定する
という3つのステップを踏むことになり、それぞれの要素を適切に決定する必要があります。
本節では予め正常なデータ(あるいは異常が混在していても無視できるデータ) \(X = \{ x^{(1)}, \ldots, x^{(N)} \}\) が用意されているものと仮定し、そこからパラメトリックな確率モデル \(p ( x; \theta )\) の古典的なパラメータ推定を行ってデータの従うモデル \(p ( x; \hat{\theta} ( X ) )\) を構成することにします。また、異常度 \(a ( x )\) としてはいわゆる負の対数尤度 (negative log-likelihood; NLL)
ないしそれを適当に変換した値を利用することにします。このとき既存の正常なデータと新しいデータ \(x'\) がいずれも \(p ( x; \hat{\theta} )\) に従うと仮定すれば新しいデータの異常度 \(a ( x' )\) の従う確率分布を導出することができるので、その分位点 (quantile) を適当に選択して閾値とすることができます。
以下では初めに最も基本的な場合として \(x\) が(1次元の)実数である場合を考え、確率モデル \(p ( x; \theta )\) としては正規分布 \(p ( x; \mu, \sigma^2 )\) を利用します。
一変量のHotelling理論#
データ \(X = \{ x^{(1)}, \ldots, x^{(N)} \}\) (各 \(x^{(n)} \in \mathbf{R}\) ) が確率密度関数
なる一変量正規分布に独立に従うものとすると、正規分布のパラメータ \(\mu, \sigma^2\) の最尤推定量 \(\hat{\mu}, \hat{\sigma}^2\) はそれぞれ
で求めることができます。文献によっては分散 \(\sigma^2\) の推定量として不偏推定量 \(\hat{\sigma}^2_\text{ub} = \frac{N}{N - 1} \hat{\sigma}^2\) を用いることもあります。
このとき、上述した負の対数尤度は
と書けるので、これからデータ \(x\) に関連しない項と定数倍を除いた
を異常度として定義します。これは \(x\) と平均 \(\hat{\mu}\) とのEuclid距離を標準偏差 \(\hat{\sigma}\) で規格化したもの(の二乗)と思うことができます。
いま新しいデータ \(x'\) もデータ \(X\) と同じ正規分布に独立に従うものとすると、統計学の理論により、異常度 \(a ( x' )\) を定数倍した
は自由度 \((1, N - 1)\) のF分布に従うことが分かっています(一変量の場合、この統計量は Hotellingの \(T^2\) 統計量 (Hotelling's T-squared statistic) と一致しています)。また、 \(N \gg 1\) のときは \(a ( x ' )\) が近似的に自由度 \(1\) のカイ二乗分布に従うものと考えることができます。いずれの場合も異常度は正常データに対して十分に低いことが想定されますから、それぞれの分布の適当な上側 \(100 q\) パーセント点を閾値に設定し、異常度 \(a ( x' )\) がこの閾値を超えた場合は異常、そうでない場合は正常と決定することにすれば新しいデータ \(x'\) に対する異常検知を実行することができます。
例(Irisデータセットにおける萼の長さの異常検知)#
Irisデータセットを利用してHotellingの方法による一変量の異常検知を実行してみましょう。今回はクラス0 (setosa) に属する観測値の萼の長さを正常データ、クラス1 (versicolor) に属する観測値の萼の長さを新しいデータとみなすことにします。
from scipy.stats import norm, f, chi2
fig, axes = plt.subplots(1, 2, figsize=(10, 5))
axes[0].hist(x0[:, 0], color='C0')
axes[0].set_title(d['target_names'][0])
axes[0].set_xlabel(d['feature_names'][0])
axes[0].set_ylabel('frequency')
axes[1].hist(x1[:, 0], color='C1')
axes[1].set_title(d['target_names'][1])
axes[1].set_xlabel(d['feature_names'][0])
axes[1].set_ylabel('frequency')
plt.show()

ヒストグラムを確認する限りでは正常データ (setosa) が正規分布に従っていることを強く疑うに至りません。より統計的に根拠のある判断が必要な場合は正規性の検定を行うことになりますが、今回は簡単のため省略します。
正常データが正規分布に従っていることを仮定し、そのパラメータの最尤推定を行うと次のようになります。
mu00_hat = x0[:, 0].mean() # 平均の最尤推定量
sigma00_hat = ((x0[:, 0] - mu00_hat) ** 2).mean() ** 0.5 # 分散の最尤推定量の平方根
print(f'平均の最尤推定量: {mu00_hat}')
print(f'分散の最尤推定量の平方根: {sigma00_hat}')
平均の最尤推定量: 5.006
分散の最尤推定量の平方根: 0.3489469873777391
なお、一変量正規分布については同様の計算が scipy.stats.norm の fit メソッドでも実行可能です。
norm.fit(x0[:, 0])
(5.006, 0.3489469873777391)
この推定値を基に新しいデータの各点について異常度 \(a\)、および上述の定数倍した値を計算すると次のようになります。
a10 = ((x1[:, 0] - mu00_hat) / sigma00_hat) ** 2 # 異常度 a; 近似的にカイ二乗分布に従う統計量
n_data = x0.shape[0]
f10 = (n_data - 1) / (n_data + 1) * a10 # F分布に従う統計量
閾値として上側1パーセント点を採用すると、その値は次のようになります。
q = 0.01
th_f = f.ppf(1 - q, dfn=1, dfd=n_data - 1)
th_chi2 = chi2.ppf(1 - q, df=1)
print(f'F分布を用いる場合の閾値: {th_f}')
print(f'カイ二乗分布を用いる場合の閾値: {th_chi2}')
F分布を用いる場合の閾値: 7.182142580971655
カイ二乗分布を用いる場合の閾値: 6.6348966010212145
これらの閾値を用いて新しいデータの各点が異常であるかを決定した場合、異常とされたデータのインデックスは次のようになります。
np.where(f10 > th_f) # F分布によって判定した場合の異常値のインデックス
(array([ 0, 1, 2, 4, 6, 8, 12, 13, 15, 18, 21, 22, 23, 24, 25, 26, 27,
28, 33, 35, 36, 37, 41, 47]),)
np.where(a10 > th_chi2) # カイ二乗分布によって判定した場合の異常値のインデックス
(array([ 0, 1, 2, 4, 6, 8, 12, 13, 15, 18, 21, 22, 23, 24, 25, 26, 27,
28, 33, 35, 36, 37, 41, 47]),)
今回は(偶然に)どちらも同一のデータが異常値と判定されました。
F分布を用いて判定した場合の結果を推定した正規分布の情報とあわせてプロットしてみましょう。
import seaborn as sns
_data = pd.DataFrame(
columns=[d['feature_names'][0], 'target', 'anomaly'],
)
_data[d['feature_names'][0]] = np.hstack([
x0[:, 0],
x1[:, 0],
])
_data['target'] = np.hstack([
np.full(shape=(x0.shape[0],), fill_value=d['target_names'][0]),
np.full(shape=(x1.shape[0],), fill_value=d['target_names'][1]),
])
_data['anomaly'] = np.hstack([
np.full(shape=(x0.shape[0],), fill_value='setosa'), # 形式的に、正常データはすべて正常であるものとする
np.where(a10 > th_f, 'versicolor; anomaly', 'versicolor; non-anomaly') # F分布を用いて判定した結果
])
g = sns.swarmplot(
x='target', y=d['feature_names'][0], hue='anomaly',
palette={
'setosa': 'C0',
'versicolor; anomaly': 'C3',
'versicolor; non-anomaly': 'C2',
},
data=_data,
)
g.grid()
g.set_title("Anomaly Detection with Hotelling's Method")
g.axhline(mu00_hat, label='mean', color='C0') # 正常データの平均を実線で描画
g.axhline(norm.ppf(0.995, loc=mu00_hat, scale=sigma00_hat), ls='--', color='C0') # 推定した正規分布の上側0.05%点を破線で描画
g.axhline(norm.ppf(0.005, loc=mu00_hat, scale=sigma00_hat), ls='--', color='C0') # 推定した正規分布の下側0.05%点を破線で描画
plt.show()

グラフの実線は正常データ(左側;setosa)から最尤推定された(一変量)正規分布の平均、破線はその中央99%区間の境界を示しています。これを見ると、(統計的な正確性を抜きにすれば)新しいデータ(右側;versicolor)のうちでこの区間から外れるものを異常と決定しても同じ結果になるように思われます。それではなぜわざわざHotellingの \(T^2\) 統計量なる概念を持ち出しつつF分布やカイ二乗分布の計算をしたのかという疑問が出るかと思われますが、実はこのように視覚的に自明な決定境界を引けるのは一変量かせいぜい二変量の場合のみで、対してHotellingの理論は多変量の場合にも同様に拡張することができるのがポイントです。次節ではその方法と具体例を見ていきます。
多変量正規分布に従うデータにおける異常検知#
本節では、多変量正規分布に従うと考えられるデータの異常検知の方法について基本的な部分を解説します。初めに多変量の場合のHotelling理論について要点を説明した後、異常と決定されたデータにおいて各特徴の異常度を見積る方法としてMahalanobis-Taguchi法 (Mahalanobis-Taguchi system, MTS) にも簡単に触れます。
多変量のHotelling理論#
\(K\) 次元のデータ \(X = \{ \mathbf{x}^{(1)}, \ldots, \mathbf{x}^{(N)} \}\) (各 \(\mathbf{x}^{(n)} = ( x_1^{(n)}, \ldots, x_K^{(n)} )^\mathrm{T} \in \mathbf{R}^{K \times 1}\) ) が確率密度関数
なる多変量正規分布に独立に従うものとすると、正規分布のパラメータ \(\boldsymbol{\mu}, \Sigma\) の最尤推定量 \(\hat{\boldsymbol{\mu}}, \hat{\Sigma}\) はそれぞれ
で求めることができます。やはり文献によっては共分散行列 \(\Sigma\) の推定量として不偏推定量 \(\hat{\Sigma}_\text{ub} = \frac{N}{N - 1} \hat{\Sigma}\) を用いることもあります。
このとき、上述した負の対数尤度は
と書けるので、これからデータ \(\mathbf{x}\) に関連しない項と定数倍を除いた
を異常度として定義します。ここで
は \(\mathbf{R}^K\) 上における距離の定義を満たしており、 Mahalanobis距離 (Mahalanobis distance) と呼ばれます。Mahalanobis距離は共分散行列 \(\Sigma\) でばらつきが大きい方向の成分を割り引いて計算したような距離で、 \(\hat{\Sigma} = I_K\) (単位行列)のときは通常の距離(Euclid距離)に一致します。
正常データ (setosa) から最尤推定した共分散行列によるMahalanobis距離の等高線を描画してみましょう。
from sklearn.covariance import EmpiricalCovariance
emp_cov = EmpiricalCovariance().fit(x0[:, 0:2]) # MLE
fig, ax = plt.subplots(figsize=(10, 5))
# 標本と平均を描画
samples_plot = ax.scatter(x0[:, 0], x0[:, 1], color='C0')
mean_plot = ax.scatter(emp_cov.location_[0], emp_cov.location_[1], color='C0', marker='x')
# Mahalanobis距離の等高線を描画
xx, yy = np.meshgrid(
np.linspace(plt.xlim()[0], plt.xlim()[1], 100),
np.linspace(plt.ylim()[0], plt.ylim()[1], 100),
)
zz = np.c_[xx.ravel(), yy.ravel()]
mahal_emp_cov = emp_cov.mahalanobis(zz)
mahal_emp_cov = mahal_emp_cov.reshape(xx.shape)
emp_cov_contour = plt.contour(
xx, yy, np.sqrt(mahal_emp_cov), cmap=plt.cm.PuBu_r, linestyles='--',
)
ax.legend(
[emp_cov_contour.collections[1], samples_plot, mean_plot],
['Mahalanobis contour from the mean', 'samples (mean)', 'mean (setosa)'],
)
ax.set_title('Mahalanobis distance with the MLE covariance matrix')
ax.set_xlabel(d['feature_names'][0])
ax.set_ylabel(d['feature_names'][1])
plt.show()

いま新しいデータ \(\mathbf{x}'\) もデータ \(X\) と同じ正規分布に独立に従うものとすると、統計学の理論により、異常度 \(a ( \mathbf{x}' )\) を定数倍した
は自由度 \((K, N - K)\) のF分布に従うことが分かっています。また、 \(N \gg K\) のときは \(a ( x ' )\) が近似的に自由度 \(K\) のカイ二乗分布に従うものと考えることができます。いずれの場合も異常度は正常データに対して十分に低いことが想定されますから、それぞれの分布の適当な上側 \(100 q\) パーセント点を閾値に設定し、異常度 \(a ( \mathbf{x}' )\) がこの閾値を超えた場合は異常、そうでない場合は正常と決定することにすれば新しいデータ \(x'\) に対する異常検知を実行することができます。
例(Irisデータセットにおける萼の長さ・幅の異常検知)#
Irisデータセットを利用してHotellingの方法による多変量の異常検知を実行してみましょう。今回はクラス0 (setosa) に属する観測値の萼の長さと幅を正常データ、クラス1 (versicolor) に属する観測値の萼の長さと幅を新しいデータとみなすことにします。
fig, axes = plt.subplots(1, 2, figsize=(10, 5))
axes[0].scatter(x0[:, 0], x0[:, 1], color='C0')
axes[0].set_title(d['target_names'][0])
axes[0].set_xlabel(d['feature_names'][0])
axes[0].set_ylabel(d['feature_names'][1])
axes[0].grid()
axes[1].scatter(x1[:, 0], x1[:, 1], color='C1')
axes[1].set_title(d['target_names'][1])
axes[1].set_xlabel(d['feature_names'][0])
axes[1].set_ylabel(d['feature_names'][1])
axes[1].grid()
plt.show()
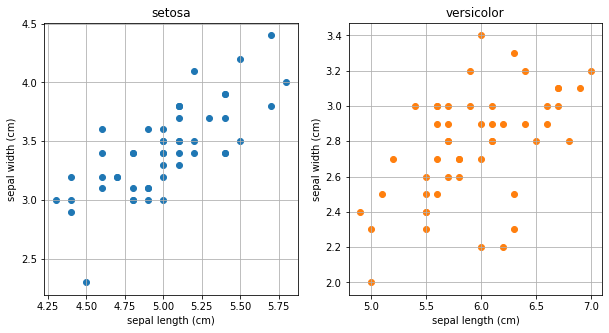
散布図を確認する限りでは正常データ (setosa) が正規分布に従っていることを強く疑うには至りません。より統計的に根拠のある判断が必要な場合は正規性の検定を行うことになりますが、今回はやはり簡単のために省略します。
正常データが正規分布に従っていることを仮定し、そのパラメータの最尤推定を行うと次のようになります。
mu0_hat = x0[:, 0:2].mean(axis=0) # 平均の最尤推定量
sigma0_hat = ((x0[:, 0:2] - mu0_hat).T @ (x0[:, 0:2] - mu0_hat)) / n_data # 共分散行列の最尤推定量の平方根
print(f'平均の最尤推定量:\n{mu0_hat}')
print(f'共分散行列の最尤推定量:\n{sigma0_hat}')
平均の最尤推定量:
[5.006 3.428]
共分散行列の最尤推定量:
[[0.121764 0.097232]
[0.097232 0.140816]]
なお、共分散行列については同様の計算が np.cov 関数でも実行可能です。
np.cov(x0[:, 0:2].T, ddof=0) # デフォルトでは不偏推定になるので最尤推定にするため ddof=0 を指定
array([[0.121764, 0.097232],
[0.097232, 0.140816]])
この推定値を基に新しいデータの各点について異常度(Mahalanobis距離) \(a\)、および上述の定数倍した値を計算すると次のようになります。
lambda0_hat = np.linalg.inv(sigma0_hat) # 共分散行列の逆行列
deviation1 = x1[:, 0:2] - mu0_hat # 新しいデータの平均からの差分
a1 = np.apply_along_axis(
lambda _d: np.dot(np.dot(_d, lambda0_hat), _d), # (n_features,)-shapedの各サンプルについて異常度を計算する
1, # _deviation[i0, :] に対して上の関数を適用した結果を a1[i0] に格納する
deviation1, # _deviation に対してこの処理を適用する
) # 異常度 a; 近似的にカイ二乗分布に従う統計量
# a1 = ((_deviation @ lambda_hat) * _deviation).sum(axis=1) # としてもよい
n_features = x1[:, 0:2].shape[1]
f1 = (n_data - n_features) / ((n_data + 1) * n_features) * a1 # F分布に従う統計量
閾値として上側1パーセント点を採用すると、その値は次のようになります。
q = 0.01
th_f_K = f.ppf(1 - q, dfn=n_features, dfd=n_data - n_features)
th_chi2_K = chi2.ppf(1 - q, df=n_features)
print(f'F分布を用いる場合の閾値: {th_f_K}')
print(f'カイ二乗分布を用いる場合の閾値: {th_chi2_K}')
F分布を用いる場合の閾値: 5.07666380708612
カイ二乗分布を用いる場合の閾値: 9.21034037197618
これらの閾値を用いて新しいデータの各点が異常であるかを決定した場合、異常とされたデータのインデックスは次のようになります。
np.where(f1 > th_f_K) # F分布によって判定した場合の異常値のインデックス
(array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33,
35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49]),)
np.where(a1 > th_chi2_K) # カイ二乗分布によって判定した場合の異常値のインデックス
(array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33,
34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49]),)
今回はF分布を用いた場合のみ34番目のデータ点が異常と判定されず、それ以外のデータ点はどちらでも異常と判定されました。
F分布を用いて判定した場合の結果を、プロットしてみましょう。
from matplotlib.patches import Ellipse
import matplotlib.transforms as transforms
fig, ax = plt.subplots(1, 1, figsize=(10, 7))
_is_anomaly = np.where(f1 > th_f_K, True, False)
ax.scatter(x0[:, 0], x0[:, 1], color='C0', label='setosa')
ax.scatter(mu0_hat[0], mu0_hat[1], color='C0', marker='x', label='setosa; ellipse center')
ax.scatter(x1[_is_anomaly, 0], x1[_is_anomaly, 1], color='C3', label='versicolor; anomaly')
ax.scatter(x1[~_is_anomaly, 0], x1[~_is_anomaly, 1], color='C2', label='versicolor; non-anomaly')
# ここから99%信頼楕円の描画
_rho = sigma0_hat[0, 1] / np.sqrt(sigma0_hat[0, 0] * sigma0_hat[1, 1])
_rad_x = np.sqrt(1. + _rho)
_rad_y = np.sqrt(1. - _rho)
_ellipse = Ellipse((0., 0.), width=_rad_x * 2, height=_rad_y * 2, ls='--', edgecolor='C0', facecolor='none')
_c = np.sqrt(chi2.ppf(0.99, df=n_features))
_scale_x = _c * np.sqrt(sigma0_hat[0, 0])
_mean_x = mu0_hat[0]
_scale_y = _c * np.sqrt(sigma0_hat[1, 1])
_mean_y = mu0_hat[1]
_transform = transforms.Affine2D().rotate_deg(45).scale(_scale_x, _scale_y).translate(_mean_x, _mean_y)
_ellipse.set_transform(_transform + ax.transData)
ax.add_patch(_ellipse)
# ここまで99%信頼楕円の描画
ax.grid()
ax.legend()
ax.set_title("Anomaly Detection with Hotelling's Method")
ax.set_xlabel(d['feature_names'][0])
ax.set_ylabel(d['feature_names'][1])
plt.show()

グラフのバツ印は正常データ(左側;setosa)から最尤推定された(二変量)正規分布の平均、破線はその中央99%楕円を示しています。グラフより、新しいデータのうちF分布を用いた判定で唯一異常でないと判断されたデータ点はこの楕円が指定する領域に近接していることが分かります。データが3次元以上の場合でも共分散行列の特異値分解を用いれば同様の(超)楕円体を求めることはできますが、新しいデータが(超)楕円体の内部に入るか否かを視覚的に判断することは最早困難ですし、数値的に判断する場合でも結局は推定された平均と共分散行列を用いてMahalanobis距離を計算することになってしまいます。初めからHotelling理論に従って異常度 \(a ( \mathbf{x}' )\) を計算した方が統計的な理論付けも得られて便利なのです。
補足:Hotellingの \(T^2\) 統計量について#
一般に、 Hotellingの \(T^2\) 統計量 (Hotelling's T-squared statistic) は多変量正規分布に従う母集団の平均に関する統計的検定の過程で現れるものです。今回の場合、
母集団1: 平均 \(\boldsymbol{\mu}_{(1)}\), 共分散行列 \(\Sigma_{(1)}\)
母集団2: 平均 \(\boldsymbol{\mu}_{(2)}\), 共分散行列 \(\Sigma_{(2)}\)
なる2つの母集団を考え、母集団1からサイズ \(n_{(1)} = 1\) の標本 \(\{ \mathbf{x}' \}\) が、母集団2からサイズ \(n_{(2)} = N\) の標本 \(X = \{ \mathbf{x}^{(1)}, \ldots, \mathbf{x}^{(N)} \}\) がそれぞれ抽出されたものとして、等分散仮定 \(\Sigma_{(1)} = \Sigma_{(2)}\) の下で
帰無仮説 \(H_0\): \(\boldsymbol{\mu}_{(1)} = \boldsymbol{\mu}_{(2)}\)
対立仮説 \(H_1\): \(\boldsymbol{\mu}_{(1)} \neq \boldsymbol{\mu}_{(2)}\)
なる統計的検定を(形式的に)実施することを考えます。このときプールされた(不偏)共分散行列は \(\frac{N + 1}{N - 1} \hat{\Sigma}\) となり、Hotellingの \(T^2\) 統計量
を得ることができます。この統計量が \(T^2\) 統計量と呼ばれるのは、データが1次元 ( \(K = 1\) ) の場合に \(t = \sqrt{T^2}\) が自由度 \(n_{(1)} + n_{(2)} - 2 = N - 1\) のStudentのt分布に従うことによります。この \(T^2\) を変換した
は自由度 \((K, N - K)\) のF分布に従うため、所望の統計的検定、およびそれを応用した異常検知の手法が可能になるのです。
式から明らかなように、2つの統計量 \(T^2\) および \(F\) は \(K = 1\) の場合(即ち、データが1次元である場合)に限って一致します。井出 (2015) ではこの \(F\) のことを「Hotellingの \(T^2\) 統計量」と呼んでいますが、一般的な使い方ではありません。また、 \(N \gg K\) の場合は \(T^2 = \frac{N - 1}{N + 1} a ( \mathbf{x}' )\) も近似的に自由度 \(K\) のカイ二乗分布に従います。
Mahalanobis-Taguchi法 (MT法)#
Hotelling理論を用いれば多変量(たとえば \(K\) 次元データ)の場合でも新しいデータ \(\mathbf{x}'\) が異常かどうかを決定できることが分かりました。いま、新しいデータ \(X' = \{ {\mathbf{x}'}^{(1)}, \ldots, {\mathbf{x}'}^{(N')} \}\) (各 \({\mathbf{x}'}^{(n')} = ( {x'}_1^{(n')}, \ldots, {x'}_K^{(n')} )^\mathrm{T} \in \mathbf{R}^{K \times 1}\) ) が与えられて、そのほとんどが異常であったとします。この新しいデータ \(X'\) の異常性は \(K\) 個の特徴のうちどの(あるいは、どの組み合わせの)寄与によるものなのでしょうか? もう少し平易に言えば、新しいデータ \(X'\) は全体としてどの特徴(の組み合わせ)が異常なのでしょうか?
Mahalanobis-Taguchi法 (MT法; Mahalanobis-Taguchi System; MTS) は、このいささか限定的な、しかし実務上はしばしば出現する疑問に対する簡便な解答を与えてくれるものです。重要な注意点として、今までのHotelling理論が標準的な統計的検定の特殊な場合として記述できたのと異なり、これから説明するMT法の計算過程は経験則によるものを多分に含みます。
Hotelling理論の考え方をもとに、全部で \(K\) 個の特徴のうち \(\mathcal{J} = \{ k_1, \ldots, k_J \} \subseteq \{ 1, \ldots, K \}\) に対応する \(J\) 個の特徴だけから計算した異常度を考えてみましょう。ここでは単に \(k_1, \ldots, k_J\) 番め以外の特徴を無視した \(J\) 次元データの異常度
を利用することにします。ただし \(\hat{\Sigma}_\mathcal{J} = P_\mathcal{J} \hat{\Sigma} P_\mathcal{J}\) は共分散行列のうち \(\mathcal{J}\) に対応するもの以外の成分を \(0\) で置き換えた行列とし、 \(P_\mathcal{J}\) は第 \(k\) 対角成分が \(k \in \mathcal{I}\) ならば \(1\)、そうでなければ \(0\) の対角行列とします。このときHotelling理論によると \(a_\mathcal{J} ( \mathbf{x}' )\) は \(N \gg J\) のとき近似的に自由度 \(J\) のカイ二乗分布(期待値 \(J\)、分散 \(2J\) )に従うので、これを特徴数で割った \(a_\mathcal{J} ( \mathbf{x}' ) / J\) が従う分布の期待値は1、分散は \(\sqrt{2 / J}\) となります。従って、例えば次のような指標
(SN比)を導入すれば、 \(\mathrm{SN}_\mathcal{J}\) が大きな正の値を取るような \(\mathcal{J} = \{ k_1, \ldots, k_J \}\) に対応する特徴の組は \(X'\) の異常性に寄与していると言えそうです。また、個別の異常データ \({\mathbf{x}'}^{(n')}\) についても \(N' = 1\) と思って
とすれば \(\mathcal{J}\) の寄与を計算することができます。なお、SN比はMT法においてよく用いられる指標ですが経験的なものであり、特に明確な統計的意味付けはありません。
\(\mathcal{J}\) として単一の特徴のみを含むもの、即ち \(\mathcal{J} = \{ k \}\) の形のもの( \(J = 1\) のもの)だけを考える場合は
となってSN比の計算も簡単ですし、考える \(\mathcal{J}\) のパターンも \(K\) 種類で済みます。 \(\mathcal{J}\) として複数の特徴を含むもの( \(J > 1\) のもの)まで考える場合は組合せ爆発によってSN比を網羅的に計算することが困難になるため、しばしば二水準の実験計画法を援用して \(X'\) の異常性に寄与する特徴の組を効率的に求めることが図られます。
例(Irisデータセットに対するMT法の適用)#
直前の例に続いて、Irisデータセットで今回はクラス0 (setosa) に属する観測値の萼の長さと幅を正常データ、クラス1 (versicolor) に属する観測値の萼の長さと幅を新しい異常なデータとみなしてMT法で単一の特徴による異常度への寄与を計算してみましょう。
# deviation1 = x1[:, 0:2] - mu0_hat # 新しいデータの平均からの差分(再掲)
a1_k = deviation1 ** 2 / np.diag(sigma0_hat) # 変数ごとに、各kに対応する異常度をまとめて計算
sn1_all_k = - 10. * np.log10((1. / a1_k).mean(axis=0)) # versicolor全体で各特徴の異常度への寄与
sn1_each_k = 10. * np.log10(a1_k) # versicolorの各データ点におけるの各特徴の異常度への寄与
まず、異常データ (versicolor) 全体でのSN比を確認してみましょう。
print(f'SNR for {d["feature_names"][0]}: {sn1_all_k[0]}.')
print(f'SNR for {d["feature_names"][1]}: {sn1_all_k[1]}.')
SNR for sepal length (cm): -21.33632561965884.
SNR for sepal width (cm): -6.348282887063784.
fig, ax = plt.subplots(1, 1, figsize=(5, 5))
_x_pos = np.arange(sn1_all_k.shape[0])
ax.bar(_x_pos, sn1_all_k.flatten(), color='C0', label='versicolor')
ax.set_title('SNR by Mahalanobis-Taguchi System')
ax.set_xlabel('features')
ax.set_ylabel('SNR')
ax.set_xticks(_x_pos)
ax.set_xticklabels(d['feature_names'][0:2])
ax.grid()
ax.legend()
plt.show()
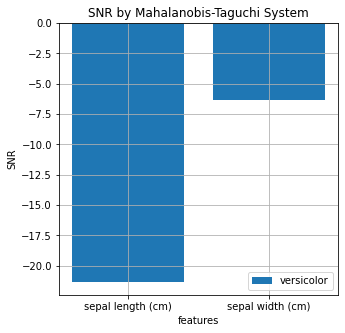
新しいデータ (versicolor) はHotellingの方法によればほぼすべてのデータ点が異常であったにもかかわらず、MT法で計算したSN比はどちらの単一の特徴についても負の値、即ち異常性に寄与しているわけではないという結果になりました。とはいえこれは直前の例で示した図と照らし合わせてみれば当然で、確かに新しいデータの分布は正常データ (setosa) とほとんど重複していませんが、それぞれの特徴についてだけ(即ち、縦軸や横軸の方向についてだけ)考えるのであれば正常データと重なっている部分が大きくなっています。
次に、異常データの各点におけるSN比の値の正負をプロットしてみましょう。
fig, ax = plt.subplots(1, 1, figsize=(10, 7))
_is_snr_pp = (sn1_each_k[:, 0] > 0.) & (sn1_each_k[:, 1] > 0.)
_is_snr_pm = (sn1_each_k[:, 0] > 0.) & (sn1_each_k[:, 1] <= 0.)
_is_snr_mp = (sn1_each_k[:, 0] <= 0.) & (sn1_each_k[:, 1] > 0.)
_is_snr_mm = (sn1_each_k[:, 0] <= 0.) & (sn1_each_k[:, 1] <= 0.)
ax.scatter(x0[:, 0], x0[:, 1], color='C0', marker='o', label='setosa')
ax.scatter(mu0_hat[0], mu0_hat[1], color='C0', marker='x', label='setosa; ellipse center')
ax.scatter(x1[_is_snr_pp, 0], x1[_is_snr_pp, 1], color='C3', marker='D', label='versicolor; SNR +, +')
ax.scatter(x1[_is_snr_pm, 0], x1[_is_snr_pm, 1], color='C3', marker='^', label='versicolor; SNR +, -')
ax.scatter(x1[_is_snr_mp, 0], x1[_is_snr_mp, 1], color='C3', marker='v', label='versicolor; SNR -, +')
ax.scatter(x1[_is_snr_mm, 0], x1[_is_snr_mm, 1], color='C3', marker='o', label='versicolor; SNR -, -')
# ここから99%信頼楕円の描画
_rho = sigma0_hat[0, 1] / np.sqrt(sigma0_hat[0, 0] * sigma0_hat[1, 1])
_rad_x = np.sqrt(1. + _rho)
_rad_y = np.sqrt(1. - _rho)
_ellipse = Ellipse((0., 0.), width=_rad_x * 2, height=_rad_y * 2, ls='--', edgecolor='C0', facecolor='none')
_c = np.sqrt(chi2.ppf(0.99, df=n_features))
_scale_x = _c * np.sqrt(sigma0_hat[0, 0])
_mean_x = mu0_hat[0]
_scale_y = _c * np.sqrt(sigma0_hat[1, 1])
_mean_y = mu0_hat[1]
_transform = transforms.Affine2D().rotate_deg(45).scale(_scale_x, _scale_y).translate(_mean_x, _mean_y)
_ellipse.set_transform(_transform + ax.transData)
ax.add_patch(_ellipse)
# ここまで99%信頼楕円の描画
ax.grid()
ax.legend()
ax.set_title("Anomaly Detection with Hotelling's Method")
ax.set_xlabel(d['feature_names'][0])
ax.set_ylabel(d['feature_names'][1])
plt.show()

新しいデータ(赤色)のうちマーカーが▲のものはsepal lengthのみ、▼のものはsepal widthのみ、◆のものはその両方が正のSN比を取るデータです(マーカーが●のものは両方が負のSN比を取るデータですが、存在しません)。明らかに、各特徴について正常データの平均(青色のバツ印)に近い点でのみSN比が負の値を取り、そうでない場合は正の値を取っていることがわかります。
小括#
本稿では正常データが正規分布に従う場合の異常検知の手法について解説し、あわせて異常データにおける各特徴の異常性への寄与を測る経験則としてMT法を紹介しました。データが正規分布に従うという仮定は頻用されるものですが、データによってはそうでない場合も多々あります。とはいえその場合もデータの従う分布さえ取り替えてやれば(正規分布の場合より複雑になりますが)同様の方法、即ち確率モデルの負の対数尤度をもとに異常度を定めるという方法は適用できます。また、元のデータの中に無視できない異常データが混在している場合も異常データの従う分布との混合モデルを考えることで同様の方法に落とし込むことができます。これらの発展的な手法については機会があれば記事を改めて解説します。
参考文献#
井出 (2015). 入門 機械学習による異常検知 - Rによる実践ガイド -. コロナ社.
STAT 505 | Applied Multivariate Statistical Analysis
Lesson 7: Inferences Regarding Multivariate Population Mean

