基本的な時系列回帰モデル#
本稿では、DCSデータのような離散時間の系列データの予測において基本となる、いくつかの線形な時系列回帰モデルについて簡単に説明します。従来、こうした系列データの解析は統計的時系列解析を筆頭に計量経済学、力学系、信号処理、システム同定などの分野でそれぞれの問題意識の下に行われてきたため、その中で使われる用語や概念にもしばしば異同や重複が存在します。本稿では主に計量経済学とシステム同定の知見に拠りつつ、必要に応じて他分野の知見も紹介する形での説明を目指します。
import datetime
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
import statsmodels.tsa.api as tsa
import statsmodels.graphics.tsaplots as tsaplots
%matplotlib inline
plt.rcParams['font.family'] = 'Hiragino Maru Gothic Pro' # 日本語を表示できるフォントを指定
pd.plotting.register_matplotlib_converters()
import warnings
warnings.filterwarnings('ignore')
準備#
一変量の時系列 \(y = (y_0, y_1, \ldots ) = ( y_t )_{t = 0, 1, \ldots}\) に興味があり、その時刻 \(t - 1\) までの値 \((y_0, \ldots, y_{t - 1})\) を用いて \(n\) ステップ先の値、即ち時刻 \(t - 1 + n\) での値 \(y_{t - 1 + n}\) を推測したいものとします。
また、この際、副次的な情報として他の時系列 \(x_k = ( x_{k, 0}, x_{k, 1}, \ldots ) = ( x_{k, t} )_{t = 0, 1, \ldots}\) の値を \(k = 1, \ldots, K\) について利用してもよいものとします。
df = pd.read_csv('../data/2020413.csv', index_col=0, parse_dates=True, encoding='cp932')
df.head(10)
| 気化器圧力_PV | 気化器圧力_SV | 気化器圧力_MV | 気化器液面レベル_PV | 気化器液面レベル_SV | 気化器液面レベル_MV | 気化器温度_PV | 気化器ヒータ出口温度_PV | 気化器ヒータ出口温度_SV | 気化器ヒータ熱量_MV | ... | 反応器流入組成(CO2)_PV | 反応器流入組成(C2H4)_PV | 反応器流入組成(C2H6)_PV | 反応器流入組成(VAc)_PV | 反応器流入組成(H2O)_PV | 反応器流入組成(HAc)_PV | セパレータ蒸気排出量_MV (Fixed) | アブソーバスクラブ流量_MV (Fixed) | アブソーバ還流流量_MV (Fixed) | 気化器液体流入量_MV (Fixed) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2020-04-13 00:00:00 | 127.983294 | 127.883920 | 18.728267 | 0.700204 | 0.7 | 21876.987772 | 120.159558 | 151.274003 | 150.0 | 9008.540694 | ... | 0.006273 | 0.585715 | 0.214016 | 0.001370 | 0.008524 | 0.109444 | 16.1026 | 15.1198 | 0.766 | 2.1924 |
| 2020-04-13 00:00:01 | 128.262272 | 127.807691 | 18.728267 | 0.700865 | 0.7 | 21876.987772 | 120.072575 | 151.218620 | 150.0 | 9008.540694 | ... | 0.006286 | 0.585342 | 0.213945 | 0.001368 | 0.008512 | 0.109441 | 16.1026 | 15.1198 | 0.766 | 2.1924 |
| 2020-04-13 00:00:02 | 127.899077 | 127.991074 | 19.079324 | 0.699740 | 0.7 | 21918.359526 | 120.305327 | 151.201067 | 150.0 | 8886.272509 | ... | 0.006281 | 0.584384 | 0.215043 | 0.001373 | 0.008541 | 0.109871 | 16.1026 | 15.1198 | 0.756 | 2.1924 |
| 2020-04-13 00:00:03 | 127.622218 | 127.990697 | 18.772228 | 0.699970 | 0.7 | 21892.166478 | 120.219488 | 151.220816 | 150.0 | 8806.115271 | ... | 0.006289 | 0.584467 | 0.214126 | 0.001372 | 0.008573 | 0.109775 | 16.1026 | 15.1198 | 0.746 | 2.1924 |
| 2020-04-13 00:00:04 | 127.577243 | 127.903788 | 18.605173 | 0.700939 | 0.7 | 21885.688813 | 120.302267 | 151.165624 | 150.0 | 8750.295310 | ... | 0.006313 | 0.584698 | 0.214002 | 0.001374 | 0.008547 | 0.109868 | 16.1026 | 15.1198 | 0.766 | 2.1924 |
| 2020-04-13 00:00:05 | 128.183048 | 127.934594 | 18.583280 | 0.699651 | 0.7 | 21927.678085 | 120.208456 | 151.242158 | 150.0 | 8718.212707 | ... | 0.006256 | 0.584795 | 0.214526 | 0.001373 | 0.008527 | 0.109651 | 16.1026 | 15.1198 | 0.766 | 2.1924 |
| 2020-04-13 00:00:06 | 128.245161 | 127.901869 | 18.710301 | 0.699443 | 0.7 | 21894.143598 | 120.309556 | 151.179828 | 150.0 | 8688.756816 | ... | 0.006274 | 0.585834 | 0.213839 | 0.001368 | 0.008492 | 0.109456 | 16.1026 | 15.1198 | 0.756 | 2.1924 |
| 2020-04-13 00:00:07 | 128.032270 | 127.868039 | 18.887724 | 0.699686 | 0.7 | 21861.818631 | 120.092940 | 151.318649 | 150.0 | 8674.959252 | ... | 0.006254 | 0.585642 | 0.213825 | 0.001370 | 0.008549 | 0.109546 | 16.1026 | 15.1198 | 0.766 | 2.1924 |
| 2020-04-13 00:00:08 | 127.941267 | 127.953515 | 18.932479 | 0.698598 | 0.7 | 21851.901643 | 120.139576 | 151.285644 | 150.0 | 8651.439289 | ... | 0.006291 | 0.585233 | 0.213886 | 0.001377 | 0.008562 | 0.109820 | 16.1026 | 15.1198 | 0.746 | 2.1924 |
| 2020-04-13 00:00:09 | 127.682568 | 127.864647 | 18.789235 | 0.700651 | 0.7 | 21793.262368 | 120.114008 | 151.043005 | 150.0 | 8638.631220 | ... | 0.006273 | 0.584639 | 0.214399 | 0.001376 | 0.008553 | 0.109593 | 16.1026 | 15.1198 | 0.756 | 2.1924 |
10 rows × 91 columns
今回は デカンタ温度_PV カラムに興味があるものとし、この系列を \(y\) とおきます。また、副次的な情報として セパレータ液体温度_PV および 蒸留塔第5トレイ温度_PV のカラムが利用できるものとし、それらの系列をそれぞれ \(x_1, x_2\) とおきます。
y = df['デカンタ温度_PV']
x1 = df['セパレータ液体温度_PV']
x2 = df['蒸留塔第5トレイ温度_PV']
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
ax.plot(y)
ax.grid()
本稿では主に統計的な枠組みでこの課題に取り組みます。即ち、時系列 \(y\) の従う統計的モデルを仮定し、データを用いてその下での統計的推測を行い、 \(y_t\) の値を一般の統計的な意味で予測する(predict)か、時系列解析的な意味で予測する(forecast)方法について考えます。
簡単のため、当面は一ステップ予測について考えます。言い換えると、時系列 \(y\) の時刻 \(t - 1\) までの値 \((y_0, \ldots, y_{t - 1})\) を用いて一ステップ先の値、即ち時刻 \(t - 1 + 1 = t\) での値 \(y_t\) を推測したいものとします。
自己回帰モデル#
興味のある時系列 \(y\) について、各時刻での \(y_t\) の値は雑音を除いて直前 \(p\) ステップの時刻での値にのみ直接依存すると仮定します。いま、その依存関係が線形であるとすると
と表すことができます。ここで \(\epsilon_t\) はホワイトノイズとします。このモデルを \(p\) 次の 自己回帰モデル (autoregressive model, AR) と呼び、しばしば AR(\(p\)) などと表します。
AR(\(p\)) モデルで健全な推定を行うためにはいくつかの仮定が要請されますが、少なくとも系列 \(y_t\) は定常である必要があります。また、系列 \(y_t\) の自己相関はラグが十分大きくなるにつれてゼロに近付く必要があります。
係数の決定#
自己回帰モデルの次数 \(p\) を既知とします。このとき AR(\(p\)) のパラメータ \(( c, \phi_1, \ldots, \phi_p )\) を決定する方法はいくつかあり、最も単純には通常の最小二乗法(ordinary least squares method, OLS)によります。即ち、訓練データとして利用可能な \(( y_t, y_{t - 1}, \ldots, y_{t - p} )\) の組について、損失
を最小化する \(( c, \phi_1, \ldots, \phi_p )\) の組を求めます。
p = 8
scikit-learnの LinearRegression クラスを用いた実装は次のようになります:
y_lagged_index_ar = np.arange(p)[::-1].reshape(1, -1) + np.arange(y.shape[0] - p).reshape(-1, 1)
y_lagged_ar = y.values[y_lagged_index_ar] # 説明変数、(T - p, p)-行列
y_target_ar = y.values[p:].reshape(-1, 1) # 目的変数、(T - p, 1)-行列
skl_ar = LinearRegression()
skl_ar.fit(y_lagged_ar, y_target_ar) # OLSでfitting
LinearRegression()
print(f'OLS fitting of the AR({p}) model with scikit-learn::')
print(f'* c: {skl_ar.intercept_}.')
print(f'* phi: {skl_ar.coef_}.')
OLS fitting of the AR(8) model with scikit-learn::
* c: [13.72098554].
* phi: [[ 1.60537596 -0.96073816 0.20676075 -0.13635203 0.05930771 -0.05406117
0.04374921 -0.06333299]].
統計的推測でパラメータを決定する場合は何通りかの方法が考えられます。AR(\(p\)) モデルの統計的推測で問題となるのは最初の \(p\) ステップの扱いで、単純に全系列の尤度を計算しようとすると \(f ( y_0, \ldots, y_{p - 1} )\) が因数として残ってしまいます。最初の \(p\) ステップの値を所与とした条件付きの最尤推定を行えばこの因数は無視でき、さらに \(\epsilon_t\) がGaussianであればこの推測はOLSと等価になります。一方、 AR(\(p\)) モデルの定める定常過程から \(( y_0, \ldots, y_{p - 1} )\) の定常同時分布を求め、その尤度を利用して数値的に尤度を最小化することもできます。
statsmodelsを利用する場合、クラス tsa.AutoReg では前者、クラス tsa.SARIMAX では後者の方法でそれぞれ推定が行われます。
sm_ar = tsa.AutoReg(endog=y.values, lags=p)
sm_ar_rlt = sm_ar.fit()
print(f'Conditional MLE fitting of the AR({p}) model with statsmodels::')
print(f'* c: {sm_ar_rlt.params[0]}.')
print(f'* phi: {sm_ar_rlt.params[1:]}.')
Conditional MLE fitting of the AR(8) model with statsmodels::
* c: 13.720985540383005.
* phi: [ 1.60537596 -0.96073816 0.20676075 -0.13635203 0.05930771 -0.05406117
0.04374921 -0.06333299].
予測#
適当な方法で決定されたAR(\(p\)) モデルのパラメータ \(( \hat{c}, \hat{\phi}_1, \ldots, \hat{\phi}_p )\) と時刻 \(t - 1\) までの \(y\) の値 \(( y_{t - 1}, \ldots, y_{t - p} )\) が与えられたとき、これらを元の式にプラグインした
によって得られる \(\hat{y}_t\) を時刻 \(t\) における \(y\) の値の予測とします。
scikit-learnの LinearRegression クラスを用いた実装は次のようになります:
y_target_skl_ar_pred = skl_ar.predict(y_lagged_ar)
_fig, _ax = plt.subplots(1, 1, figsize=(10, 5))
_begin = 60
_window = 120
_lag= p
_ax.set_title('In-sample forecast with AR / scikit-learn')
_ax.plot(
y.index[_begin:(_begin + _window)],
y_target_ar[(_begin - _lag):(_begin - _lag + _window)],
label='true',
)
_ax.plot(
y.index[_begin:(_begin + _window)],
y_target_skl_ar_pred[(_begin - _lag):(_begin - _lag + _window)],
label='pred (sklearn)',
)
_ax.grid()
_ax.legend()
plt.show()

statsmodelsの AutoReg クラスを利用した予測は次のようになります:
y_sm_ar_pred = sm_ar_rlt.predict() # 引数なしで呼ぶとin-sample予測を実行
# y_sm_ar_pred = sm_ar_rlt.fittedvalues # 同じ値の格納されている属性
_fig, _ax = plt.subplots(1, 1, figsize=(10, 5))
_begin = 60
_window = 120
_ax.set_title('In-sample forecast with AR / statsmodels')
_ax.plot(
y.index[_begin:(_begin + _window)],
sm_ar.endog.flatten()[_begin:(_begin + _window)],
label='true',
)
_ax.plot(
y.index[_begin:(_begin + _window)],
y_sm_ar_pred[(_begin - p):(_begin + _window - p)],
label='pred (statsmodels)',
)
_ax.grid()
_ax.legend()
plt.show()
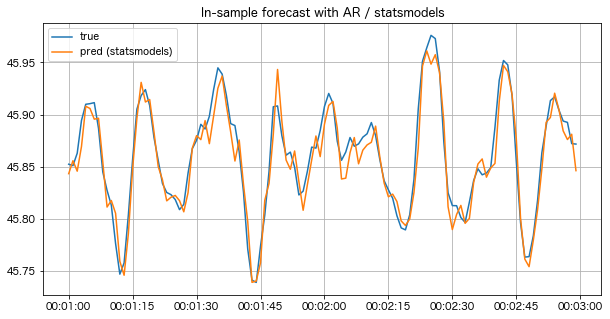
両者の利点・欠点はそれぞれいくつかあるため、必要に応じて使い分けるのがよいでしょう。
scikit-learnの LinearRegression を使った実装では学習した係数・モデルを容易に訓練データと全く異なる期間のデータに適用して予測(predict)できます。また、scikit-learnの他のオブジェクトと組み合わせてパイプラインを構成したり、交差検証を行ったりすることも容易です。一方、あくまで線形回帰のOLSと同様の計算を行うためにクラスを流用しているだけなので、時系列データを処理する上で適切な統計量や評価指標の計算は別途実装する必要があります。
statsmodelsの AutoReg クラスでは学習した係数・モデルに関する主要な統計量や評価指標が予め計算されているか、容易に計算できます。ただし、statsmodelsモジュール自体が伝統的な時系列解析の文脈での利用を想定していることもあり、in-sample予測(forecast)や(擬似)out-of-sample予測(forecast)以外の予測にモデルを利用することはやや困難です。
分布ラグモデル#
自己回帰モデルでは興味がある時系列 \(y\) の過去の値のみを用いて統計的モデルを構築しましたが、データを生成した系の特徴や解析の目的によっては他の時系列 \(x_k\) たちの値のみを用いて統計的モデルを構築する場合もあります。各時刻での \(y_t\) の値が雑音を除いて \(r_k\) ステップ前までの時系列 \(x_k\) たちの値にのみ直接依存し、その依存関係が線形であるとすると
と表すことができます。やはり \(\epsilon_t\) はホワイトノイズとしますが、この仮定は緩めることができます。このようなモデルを、特に計量経済学の分野では 分布ラグモデル (distributed lag model, DL)と呼びます。システム同定の分野では単に 線形回帰モデル (linear regression model)と呼ばれることもあります。上式では予測と同時刻の値 \(x_{k, 0}\) の項を利用していませんが、解析の目的によっては利用しても構いません。
\(K = 1\) のとき、対応する(同時刻の情報を利用する)分布ラグモデルは
となります。 \(c = 0\) であれば、これは(雑音を無視して)信号処理における有限インパルス応答 (finite impulse response, FIR) のフィルタに対応します。
分布ラグモデルで健全な推定を行うためにはいくつかの仮定が要請されますが、少なくとも系列 \(y_t, x_{1, t}, \ldots, x_{K, t}\) は結合定常である必要があります。また、系列 \(y_t, x_{1, t}, \ldots, x_{K, t}\) たちの自己相関や相互相関はラグが十分大きくなるにつれてゼロに近付く必要があります。各系列の間に完全な多重共線性が存在してもいけません。
分布ラグモデルにおけるノイズ \(\epsilon_t\) の性質について、白色性の仮定は主にOLS推定量の有効性を保証したり、推定したモデルに関する検定を実行する上で要請されるものです。OLS推定量の一致性や不偏性に関してはより緩めた仮定の下で保証することができ、例えば系列 \(x_{1, t}, \ldots, x_{K, t}\) たちが \(\epsilon_t\) と独立であれば十分です。
係数の決定#
分布ラグモデルの次数 \(r_k\) をすべて既知とします。このとき分布ラグモデルのパラメータ \((c, \beta_{1, 1}, \ldots, \beta_{K, r_K})\) は(定常性に関する仮定の下で)OLSによって求めることができます。勿論、このとき統計的には \(\epsilon_t\) のGauss性を仮定していることになります。
r1 = 5
r2 = 7
scikit-learnの LinearRegression クラスを用いた実装は次のようになります(基本的にARモデルのときと同様です):
rmax = max(r1, r2)
x1_lagged_index_dl = np.arange(r1)[::-1].reshape(1, -1) + np.arange(x1.shape[0] - rmax).reshape(-1, 1)
x1_lagged_dl = x1.values[x1_lagged_index_dl] # (T - rmax, r1)-行列
x2_lagged_index_dl = np.arange(r2)[::-1].reshape(1, -1) + np.arange(x2.shape[0] - rmax).reshape(-1, 1)
x2_lagged_dl = x2.values[x2_lagged_index_dl] # (T - rmax, r2)-行列
x_lagged_dl = np.concatenate(
(x1_lagged_dl, x2_lagged_dl),
axis=1,
) # 説明変数、(T - rmax, r1 + r2)-行列
y_target_dl = y.values[rmax:].reshape(-1, 1) # 目的変数、(T - rmax, 1)-行列
skl_dl = LinearRegression()
skl_dl.fit(x_lagged_dl, y_target_dl) # OLSでfitting
LinearRegression()
print(f'OLS fitting of the distributed lag model with scikit-learn::')
print(f'* c: {skl_dl.intercept_}.')
print(f'* beta1: {skl_dl.coef_[:, :r1]}.')
print(f'* beta2: {skl_dl.coef_[:, r1:]}.')
OLS fitting of the distributed lag model with scikit-learn::
* c: [168.83412202].
* beta1: [[0.00293575 0.00317987 0.00344324 0.00297723 0.00254693]].
* beta2: [[-0.08739845 -0.19471974 -0.24268612 -0.23535894 -0.18941955 -0.12281001
-0.05116993]].
予測#
ARモデルのときと同様、データから決定した係数をプラグインして誤差項を無視した式によって予測を行います。scikit-learnでの実装は以下の通りです:
y_target_skl_dl_pred = skl_dl.predict(x_lagged_dl)
_fig, _ax = plt.subplots(1, 1, figsize=(10, 5))
_begin = 60
_window = 120
_lag = rmax
_ax.set_title('In-sample forecast with DL / scikit-learn')
_ax.plot(
y.index[_begin:(_begin + _window)],
y_target_dl[(_begin - _lag):(_begin - _lag + _window)],
label='true',
)
_ax.plot(
y.index[_begin:(_begin + _window)],
y_target_skl_dl_pred[(_begin - _lag):(_begin - _lag + _window)],
label='pred (sklearn)',
)
_ax.grid()
_ax.legend()
plt.show()
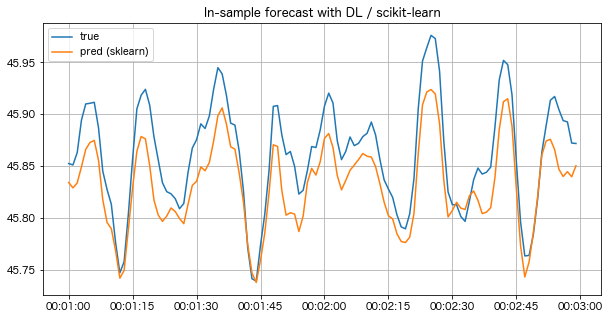
自己回帰分布ラグモデル#
ARモデルと分布ラグモデルは加法的に組み合わせることができ、そのモデルは
と表すことができます。やはり \(\epsilon_t\) はホワイトノイズとします。このようなモデルを計量経済学の分野では 自己回帰分布ラグモデル (autoregressive distributed lag model, ADL)と呼びます。
\(K = 1\) のとき、対応する(同時刻の情報を利用する)ADLモデルは
となります。 \(c = 0\) であれば、これは(雑音を無視して)信号処理における無限インパルス応答 (infinite impulse response, IIR) のフィルタに対応します。
ADLモデルで健全な推定を行うためにはいくつかの仮定が要請されますが、少なくとも系列 \(y_t, x_{1, t}, \ldots, x_{K, t}\) は結合定常である必要があります。また、系列 \(y_t, x_{1, t}, \ldots, x_{K, t}\) たちの自己相関や相互相関はラグが十分大きくなるにつれてゼロに近付く必要があります。各系列の間に完全な多重共線性が存在してもいけません。
係数の決定#
自己回帰および分布ラグの次数をすべて既知とします。このときADLモデルのパラメータ \((c, \phi_1, \ldots, \phi_p, \beta_{1, 1}, \ldots, \beta_{K, r_K})\) は(定常性に関する仮定の下で)OLSによって求めることができます。統計的には、これは \(\epsilon_t\) のGauss性を仮定して条件付きの最尤推定を行なっていることに相当します。
# p = 8
# r1 = 5
# r2 = 7
scikit-learnの LinearRegression クラスを用いた実装は次のようになります(基本的にARモデルのときと同様です):
prmax = max(p, r1, r2)
y_lagged_index_adl = np.arange(p)[::-1].reshape(1, -1) + np.arange(y.shape[0] - prmax).reshape(-1, 1)
y_lagged_adl = y.values[y_lagged_index_adl] # (T - prmax, p)-行列
x1_lagged_index_adl = np.arange(r1)[::-1].reshape(1, -1) + np.arange(x1.shape[0] - prmax).reshape(-1, 1)
x1_lagged_adl = x1.values[x1_lagged_index_adl] # (T - prmax, r1)-行列
x2_lagged_index_adl = np.arange(r2)[::-1].reshape(1, -1) + np.arange(x2.shape[0] - prmax).reshape(-1, 1)
x2_lagged_adl = x2.values[x2_lagged_index_adl] # (T - prmax, r2)-行列
yx_lagged_adl = np.concatenate(
(y_lagged_adl, x1_lagged_adl, x2_lagged_adl),
axis=1,
) # 説明変数、(T - prmax, p + r1 + r2)-行列
y_target_adl = y.values[prmax:].reshape(-1, 1) # 目的変数、(T - prmax, 1)-行列
skl_adl = LinearRegression()
skl_adl.fit(yx_lagged_adl, y_target_adl)
LinearRegression()
print(f'OLS fitting of the ADL model with scikit-learn::')
print(f'* c: {skl_adl.intercept_}.')
print(f'* phi: {skl_adl.coef_[:, :p]}.')
print(f'* beta1: {skl_adl.coef_[:, p:(p + r1)]}.')
print(f'* beta2: {skl_adl.coef_[:, (p +r1):]}.')
OLS fitting of the ADL model with scikit-learn::
* c: [25.056137].
* phi: [[ 0.74747963 0.2419992 -0.20463067 -0.07701368 -0.00936568 -0.05517905
-0.06889577 0.04165148]].
* beta1: [[0.00024745 0.00071288 0.00043726 0.00051395 0.00023536]].
* beta2: [[-0.09005841 -0.05725569 -0.00555248 0.01779025 0.02800802 0.02665245
0.01187423]].
予測#
ARモデルや分布ラグモデルのときと同様、データから決定した係数をプラグインして誤差項を無視した式によって予測を行います。scikit-learnでの実装は以下の通りです:
y_target_skl_adl_pred = skl_adl.predict(yx_lagged_adl)
_fig, _ax = plt.subplots(1, 1, figsize=(10, 5))
_begin = 60
_window = 120
_lag = prmax
_ax.set_title('In-sample forecast with ADL / scikit-learn')
_ax.plot(
y.index[_begin:(_begin + _window)],
y_target_adl[(_begin - _lag):(_begin - _lag + _window)],
label='true',
)
_ax.plot(
y.index[_begin:(_begin + _window)],
y_target_skl_adl_pred[(_begin - _lag):(_begin - _lag + _window)],
label='pred (sklearn)',
)
_ax.grid()
_ax.legend()
plt.show()

「外生変数のある自己回帰モデル」について#
統計的時系列解析やシステム同定の分野では 外生変数のある自己回帰モデル (autoregressive model with exogenous inputs, ARX) という用語が使われることがありますが、その定義は分野によって微妙に異なります。システム同定の分野におけるARXモデルは一般に上記の計量経済学におけるADLモデルと(形式的には)同一のものを指します。一方、統計的時系列解析におけるARXモデルは一般に
のように表せるモデルのことを指します。ここで \(\beta_0, \beta_1, \ldots, \beta_K\) はラグに依存しない係数です。また \(\epsilon_t\) はホワイトノイズとします。これは興味のある変数 \(y_t\) を同時刻の外生変数 \(x_{k, t}\) たちで回帰した残差の系列に対して通常のARモデルを適用していることに相当します。
Matlabのシステム同定ツールボックスのARMAXモデルやRの sysid パッケージの armax は前者の実装になっています。一方、Pythonのstatsmodelsパッケージの SARIMAX やRの forecast パッケージにおける Arima においては後者の実装になっています。
多ステップ予測#
ここまでの話は一ステップ予測についてものでした。即ち時系列 \(y\) については時刻 \(t - 1\) までの値 \((y_0, \ldots, y_{t - 1})\) を用いて副次的な情報 \(x_{k, t}\) たちについては時刻 \(t - 1\) までの(問題設定によっては時刻 \(t\) までの)値を用いて、一ステップ先の値、即ち時刻 \(t - 1 + 1 = t\) での値 \(y_t\) を推測したいものとして話を進めてきました。本節では、同様の情報を用いて \(n\) ステップ先の値、即ち時刻 \(t - 1 + n\) での値 \(y_{t - 1 + n}\) を推測したい場合の方法について考えます。
多ステップ予測の方法は大きく分けて2つあります:
繰り返し予測: 一ステップ予測を \(n\) 回繰り返すことで \(n\) ステップ先の予測を行う
直接予測: \(n\) ステップ先の値を直接予測するモデルを利用する
繰り返し予測#
本稿で記述した範囲だと、ARモデルは一ステップ予測を繰り返し行うことで任意の \(n\) ステップ先の \(y\) の値を予測することができます。即ち、まず時刻 \(t - 1\) までの値 \(( y_{t - 1}, y_{t - 2}, \ldots, y_{t - p} )\) から時刻 \(t\) の値を予測して \(\hat{y}_t\) を求め、次に時刻 \(t\) までの値 \(( \hat{y}_t, y_{t - 1}, \ldots, y_{t - p + 1} )\) から同様に時刻 \(t + 1\) の値を予測して \(\hat{y}_{t + 1}\) を求め、という手順を繰り返すことで次々に予測 \(\hat{y}_{t - 1 + n}\) を求めることができます。
n = 2
statsmodelsの AR クラスを利用した繰り返し予測は次のようになります:
y_sm_ar_pred2 = np.array([
sm_ar_rlt.predict(t, t + (n - 1), dynamic=True)[-1] # 時刻 t + (n - 1) の値をn-step予測
for t in range(p, sm_ar.endog.shape[0] - (n - 1)) # t = p, ..., T - (n - 1) - 1について
]) # 結局、時刻 p + (n - 1), ..., T - 1のn-step予測値が格納
_fig, _ax = plt.subplots(1, 1, figsize=(10, 5))
_begin = 60
_window = 120
_lag = p
_step = 2
_ax.set_title('In-sample 2-step forecast with AR / statsmodels')
_ax.plot(
y.index[_begin:(_begin + _window)],
sm_ar.endog.flatten()[_begin:(_begin + _window)],
label='true',
)
_ax.plot(
y.index[_begin:(_begin + _window)],
y_sm_ar_pred2[(_begin - _lag - (_step - 1)):(_begin - _lag - (_step - 1) + _window)],
label='pred (statsmodels)',
)
_ax.grid()
_ax.legend()
plt.show()

一方、(同時刻の副次的な情報を用いない)分布ラグモデルやADLモデルでは、時刻 \(t + 1\) の \(y\) の値を予測するために時刻 \(t\) での各 \(x_{k, t}\) の値が必要になります。これらの値が未知である場合、分布ラグモデルやADLモデルはこの予測値 \(\hat{x}_{k, t}\) を提供しないため繰り返し予測を行うことができません。副次的な情報を含めたモデルで繰り返し予測を行うには、別に記述するベクトル自己回帰モデル (vector autoregressive model, VAR)などのモデルを利用する必要があります。
直接予測#
ADLモデル、あるいはシステム同定の分野におけるARXモデルをもとにした \(n\) ステップ先の直接予測は、例えば
のように表すことができます。 ここで \(\epsilon_t\) は性質のよい適当な雑音とします。このモデルの係数 \(c, \phi_\tau, \beta_{k, \tau}\) たちの決定もしばしばOLSにより、決定された係数による予測 \(\hat{y}_{t - 1 + n}\) の計算もADLモデルと同様にします。
# n = 2
scikit-learnの LinearRegression クラスを用いた実装は次のようになります:
# コメントアウト部は「自己回帰分布ラグモデル」で行ったのと同じ処理
# prmax = max(p, r1, r2)
# y_lagged_index_adl = np.arange(p)[::-1].reshape(1, -1) + np.arange(y.shape[0] - prmax).reshape(-1, 1)
# y_lagged_adl = y.values[y_lagged_index_adl]
# x1_lagged_index_adl = np.arange(r1)[::-1].reshape(1, -1) + np.arange(x1.shape[0] - prmax).reshape(-1, 1)
# x1_lagged_adl = x1.values[x1_lagged_index_adl]
# x2_lagged_index_adl = np.arange(r2)[::-1].reshape(1, -1) + np.arange(x2.shape[0] - prmax).reshape(-1, 1)
# x2_lagged_adl = x2.values[x2_lagged_index_adl]
# yx_lagged_adl = np.concatenate(
# (y_lagged_adl, x1_lagged_adl, x2_lagged_adl),
# axis=1,
# )
yx_lagged_adl2 = yx_lagged_adl[:-(n - 1)] # 説明変数、(T - prmax - (n - 1), p + r1 + r2)-行列
# y_target_adl = y.values[prmax:].reshape(-1, 1)
y_target_adl2 = y_target_adl[(n - 1):] # 目的変数、(T - prmax - (n - 1), 1)-行列
skl_adl2 = LinearRegression()
skl_adl2.fit(yx_lagged_adl2, y_target_adl2) # OLSでfitting
LinearRegression()
print(f'OLS fitting of the 2-step ADL model with scikit-learn::')
print(f'* c: {skl_adl2.intercept_}.')
print(f'* phi: {skl_adl2.coef_[:, :p]}.')
print(f'* beta1: {skl_adl2.coef_[:, p:(p + r1)]}.')
print(f'* beta2: {skl_adl2.coef_[:, (p +r1):]}.')
OLS fitting of the 2-step ADL model with scikit-learn::
* c: [65.77816179].
* phi: [[ 0.56887556 -0.13235506 -0.20559943 0.06974964 -0.04542423 -0.19003874
-0.04846265 -0.03170848]].
* beta1: [[0.0010806 0.00154802 0.00117438 0.00104094 0.00086913]].
* beta2: [[-0.10871091 -0.09601585 -0.05142007 -0.00668014 0.03012062 0.03524233
0.02041322]].
y_target_skl_adl2_pred = skl_adl2.predict(yx_lagged_adl2)
_fig, _ax = plt.subplots(1, 1, figsize=(10, 5))
_begin = 60
_window = 120
_lag = prmax
_step = 2
_ax.set_title('In-sample 2-step forecast with ADL / scikit-learn')
_ax.plot(
y.index[_begin:(_begin + _window)],
y_target_adl[(_begin - _lag):(_begin - _lag + _window)],
label='true',
)
_ax.plot(
y.index[_begin:(_begin + _window)],
y_target_skl_adl2_pred[(_begin - _lag - (_step - 1)):(_begin - _lag - (_step - 1) + _window)],
label='pred (sklearn)',
)
_ax.grid()
_ax.legend()
plt.show()
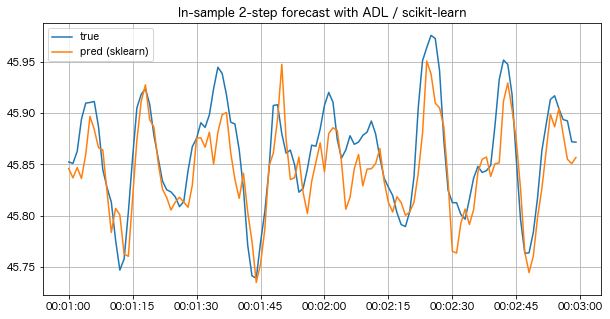
直接予測にはいくつか注意すべき点があります。一つは定常性に関する仮定があり、モデルの族や次数が正しく決定されていたとしても残差 \(\hat{y}_{t - 1 + n} - y_{t - 1 + n}\) の系列に強い自己相関が発生することです。これは現実の系である時刻に発生した外乱が複数時刻の残差に反映されるためで、予測区間を計算する際に分散不均一・自己相関一致推定 (heteroscedasticity and autocorrelation consistent estimation; HAC)といった特殊な処理が必要になります。
# ADLで一ステップ予測をした際の残差の自己相関
_ = tsaplots.plot_acf(y_target_skl_adl_pred - y_target_adl)
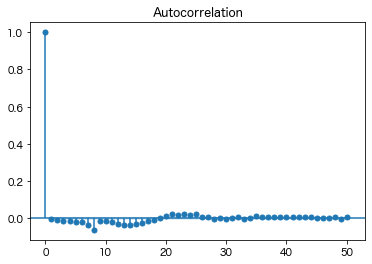
# ADLで2ステップ予測をした際の残差の自己相関
_ = tsaplots.plot_acf(y_target_skl_adl2_pred - y_target_adl[:-(n - 1)])

ほかには、繰り返し予測の場合と違って、複数の異なる \(n\) に対する \(y_{t - 1 + n}\) の予測を行う際に対応する同数の \(n\) ステップ先の直接予測のモデルが必要となることも挙げられます。これは実務上もしばしば問題になり、これゆえ特に \(K\) が大きすぎないときの短いステップの予測ではVARによる繰り返し予測の方が好まれます。一方、 \(K\) が非常に大きい場合や長いステップの予測の際にはパラメータの決定や予測精度などの理由から直接予測の方が好まれることもあります。
小括#
本稿では、計量経済学の分野で自己回帰モデル(ARモデル)、分布ラグモデル、自己回帰分布ラグモデル(ADLモデル)と呼ばれる3つの線形な時系列回帰のモデルについて、システム同定の分野における取り扱いと絡めながら、scikit-learnとstatsmodelsによる実行を含めた簡単な解説を行いました。
本稿では \(p, r_k\) などのモデルの次数を既知のものとして扱いましたが、実際の解析ではこれらの値を、あるいはそもそもどのモデルを用いるかなどを適切に選択・決定しなければなりません。そのためには、それぞれのモデルと次数における性能を適切に評価し、公平に比較するための指標が必要になります。その具体的な内容については後述する各章を参照してください。
参考文献#
Stock, J. H. and Watson M. W. (2007). Introduction to Econometrics. Pearson Education. (宮尾龍蔵 (訳, 2016). 入門計量経済学. 共立出版.)

