外れ値#
外れ値と異常値?#
統計分野では、外れ値と異常値はどちらもoutlierの訳語として用いられています。
外れ値とは、他の値と比べて、大きく外れた値のことです。
文献によっては外れ値と異常値を使い分けていることがありますが、この場合、外れ値の中でも外れ値となった理由があるものを異常値としている場合が多いです(例えば、子供の平熱を調べていたら風邪で熱を出している子が紛れ込んでしまったような場合など)。
ですので、本項では外れ値と異常値は同一視し、まとめて外れ値として取り扱いたいと思います。
外れ値の判断方法#
では、どれくらいの大きさだと外れ値とみなすのかというと、正規分布に従うような変数であれば、残差が標準偏差の2倍から3倍以上とすることが多いです。
確率的には、残差が標準偏差の2倍以上とするなら4.6%程度、3倍以上とするなら0.3%程度の出現率ということになります。
この場合は、偏差を不偏標準偏差で割った値が検定統計量として広く用いられています。
さらに精緻化した検定手法に「スミルノフ・グラブス検定」という手法があり、これは平均値から最も離れた観測値を選び、外れ値検定を行い、外れ値が見つかったら、これを除外して検定をやり直すということを続けていき、最終的には外れ値の無いデータセットを作ることも目標としています(ただし、スミルノフ・グラブス検定も正規分布を前提とした方法なので、正規分布からかけ離れた分布のデータに利用すると、観測値の殆どが外れ値になってしまうこともあるので注意してください)。
このほかにも「トンプソン検定」などもあります。標本数が十分大きいときは、この2つの検定の結果は同じになります。
残差の大きさを気にせず、無条件にデータの分布の両端から5%とか10%をカットして外れ値の混入を防ぐという方法もあります。この両端をカットして求めた平均値をトリム平均とか\(n\)%調整平均と言います。
機械的なテクニックも大事ですが、兎にも角にもヒストグラムやカーネル密度推定による初期判断も重要です。これらの利点はデータの分布も同時に確認できることです。
分布の中心が平均値よりも左側に偏り右裾の長い分布なら、外れ値を除外せず、すべてのデータを対数変換してみてください。対数変換後のデータが正規分布になり外れ値も無いようであれば、対数変換したデータを使って推定や検定を行うことで分析の精度が上がります。
どの方法を使うにしても、外れ値を除くときは外れ値が異常値でないかチェックしておきましょう。計測の失敗や風邪による高熱など異常値であることが明らかなら、除外することに問題はありません。
外れ値を異常値と判断する根拠が見つからないときは、安易に除外せず、平均値の代わりに中央値、ピアソンの相関係数の代わりに順位相関係数、検定ならノンパラメトリックな方法を利用するということも考えた方が良いかと思います。
データの読み込み#
import warnings
warnings.filterwarnings('ignore')
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
pd.set_option("display.max_rows", 10)
pd.set_option("display.max_columns", 10)
# matplotlibでは日本語にデフォルトで対応していないので、日本語対応フォントを読み込む
plt.rcParams['font.family'] = 'BIZ UDGothic' # Windows
# plt.rcParams['font.family'] = 'Hiragino Maru Gothic Pro' # Mac
# 使えるフォント一覧は以下のコードで取得できます。
# import matplotlib.font_manager
# [f.name for f in matplotlib.font_manager.fontManager.ttflist]
fpath = '../data/2020413_raw.csv'
df = pd.read_csv(fpath, index_col=0, parse_dates=True, encoding='shift-jis')
簡単化のために、「PV」と名のつく float64 列のみ使用します。
df = df.iloc[:,df.columns.str.contains('PV')]
df = df.iloc[:,list(df.dtypes == 'float64')]
# 正規化を行う
from sklearn.preprocessing import StandardScaler
# 正規化を行うオブジェクトを生成
ss = StandardScaler()
# fit_transform関数は、fit関数(正規化するための前準備の計算)と
# transform関数(準備された情報から正規化の変換処理を行う)の両方を行う
df = pd.DataFrame(ss.fit_transform(df), index=df.index, columns=df.columns)
さらに分散が1.0に正規化できなかった列を取り除きます。
df = df.iloc[:,list(df.std(axis=0) > 0.9)]
この中から外れ値がよく潜んでいる列として、min、max、25%、50%、75% がそれぞれ最小値、最大値をとっている列(計10個)を抜き出して、重複を排除して(計7個)使用します。
df = df[list(set(df.describe().loc['min':].idxmin(axis=1).tolist() + df.describe().loc['min':].idxmax(axis=1).tolist()))]
df.describe()
| 熱交換器出力温度(製品ガス)_PV | 反応器流入組成(CO2)_PV | 気化器液面レベル_PV | 水溶液レベル_PV | 反応器出口温度_PV | デカンタ温度_PV | 有機生成物レベル_PV | |
|---|---|---|---|---|---|---|---|
| count | 8.640100e+04 | 8.640100e+04 | 8.640100e+04 | 8.640100e+04 | 8.640100e+04 | 8.640100e+04 | 8.640100e+04 |
| mean | 2.635557e-15 | -3.789517e-16 | -8.962735e-14 | -2.100024e-15 | 4.136890e-15 | -6.529302e-14 | 3.157931e-17 |
| std | 1.000006e+00 | 1.000006e+00 | 1.000006e+00 | 1.000006e+00 | 1.000006e+00 | 1.000006e+00 | 1.000006e+00 |
| min | -2.471669e+00 | -1.286784e+00 | -5.456636e+00 | -1.638693e+00 | -1.454141e+00 | -2.361356e+01 | -1.411917e+00 |
| 25% | -4.976011e-01 | -9.229765e-01 | -3.207834e-01 | -1.045639e+00 | -1.255999e+00 | -6.599238e-01 | -1.243093e+00 |
| 50% | -1.853676e-01 | -1.692188e-01 | 1.138888e-01 | -2.266528e-01 | 5.895510e-01 | 9.391837e-03 | 7.453078e-01 |
| 75% | 1.466406e-01 | 6.739595e-01 | 5.303117e-01 | 1.079470e+00 | 6.523746e-01 | 6.687955e-01 | 8.018350e-01 |
| max | 4.990378e+00 | 3.860856e+00 | 3.647791e+00 | 1.362996e+00 | 2.579643e+00 | 1.072602e+01 | 9.665390e-01 |
fig = plt.figure(figsize = [8,12], dpi = 200)
fig.subplots_adjust(hspace=1.0)
for n, column in enumerate(df.columns):
subplot = fig.add_subplot(4,2,n+1)
df[column].plot(ax = subplot)
subplot.set_title(column)
plt.show()
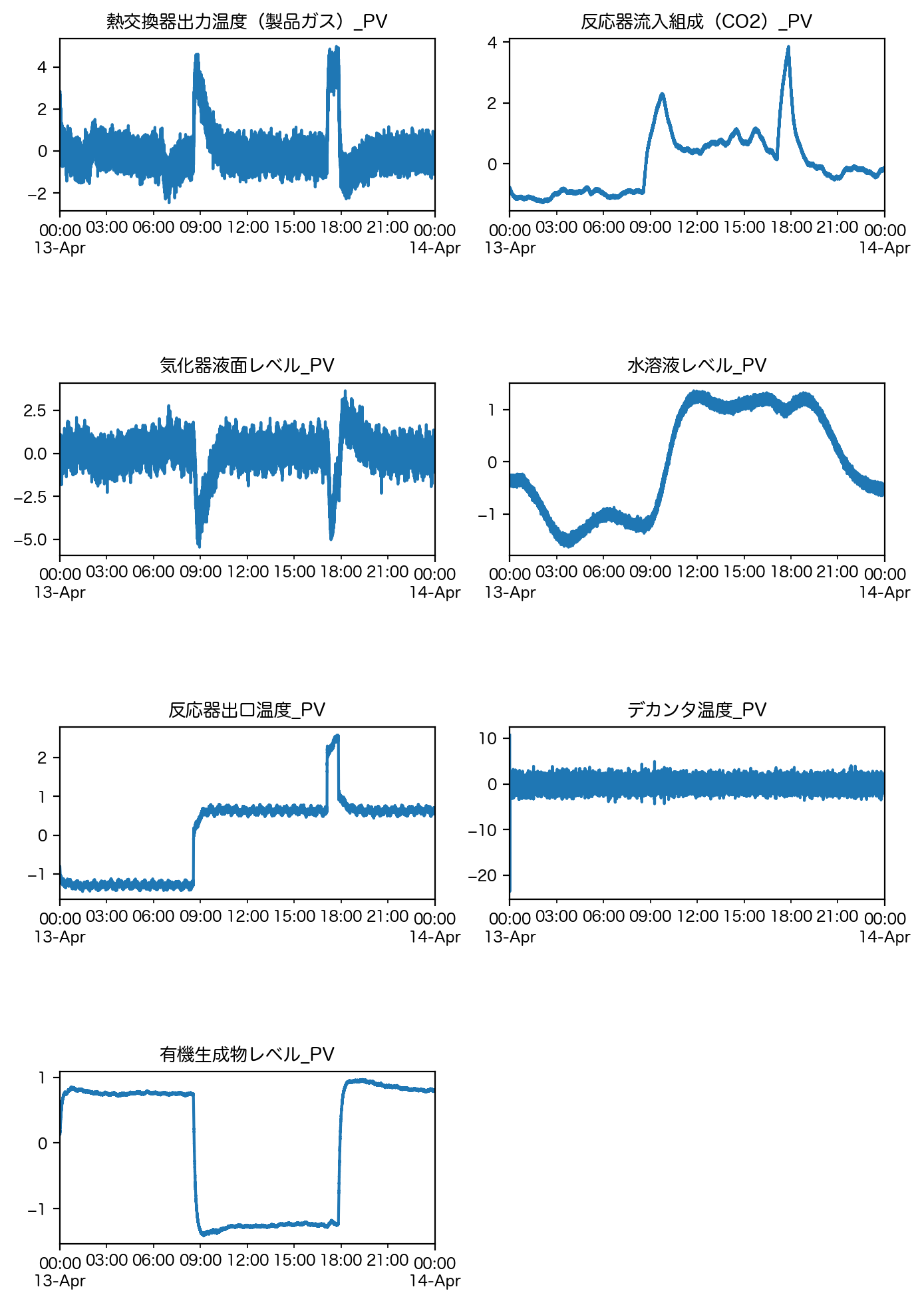
基本統計量に基づいた外れ値処理#
最初のアプローチとして、分布の可視化にはヒストグラムとカーネル密度推定を、基本統計量の可視化には箱ひげ図を確認することから始めましょう。
# ヒストグラムとカーネル密度推定
fig = plt.figure(figsize=[16, 12], dpi=200)
fig.subplots_adjust(wspace=0.5)
for n, column in enumerate(df.columns):
subplot = fig.add_subplot(2, 4, n+1)
df[column].plot.hist(ax=subplot, normed=True)
df[column].plot.kde(ax=subplot)
subplot.set_title(column)
plt.show()
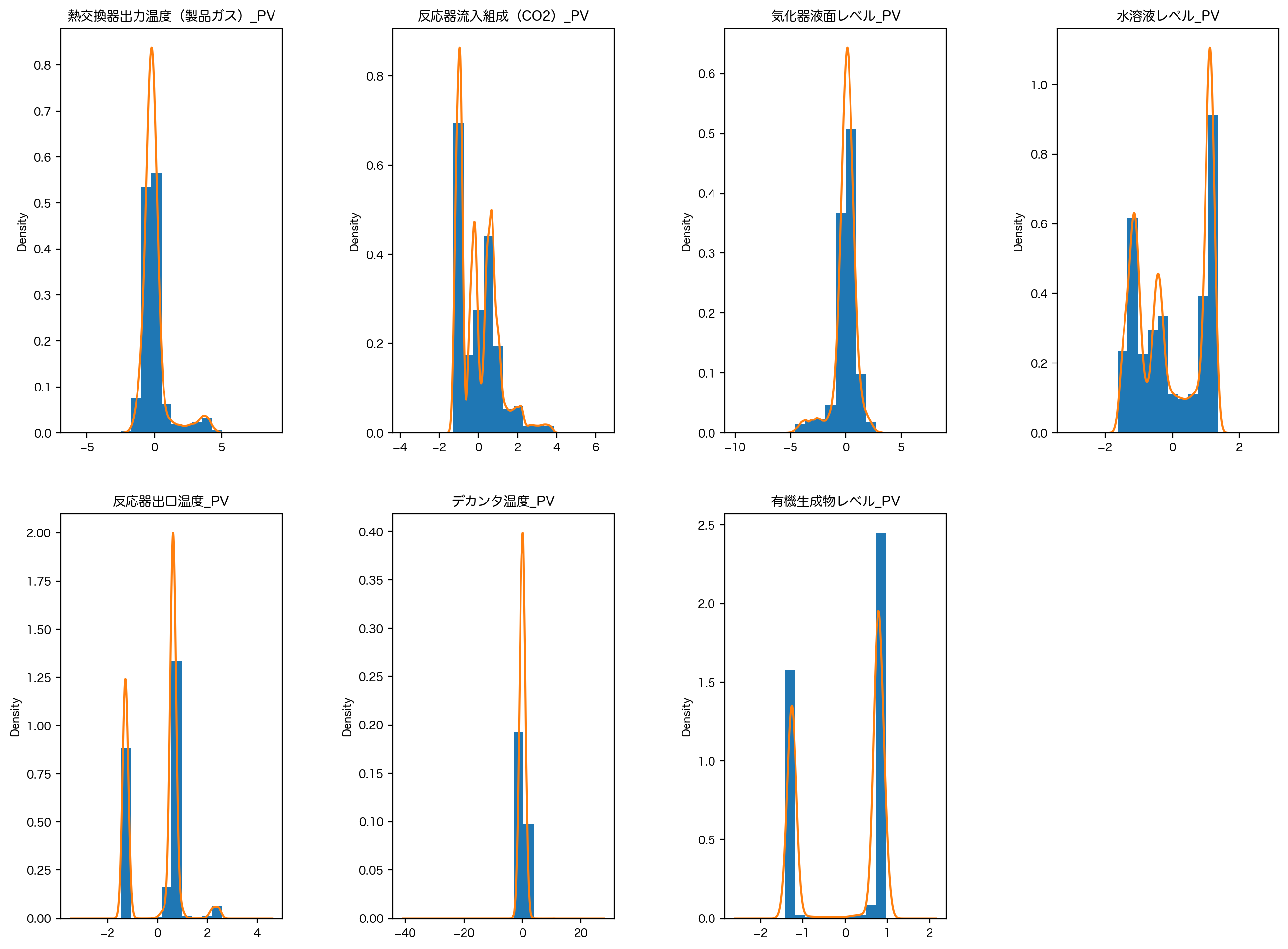
# 箱ひげ図
fig = plt.figure(figsize=[16, 12], dpi=200)
fig.subplots_adjust(wspace=0.5)
for n, column in enumerate(df.columns):
subplot = fig.add_subplot(2,4,n+1)
df[column].plot.box(ax=subplot)
plt.show()
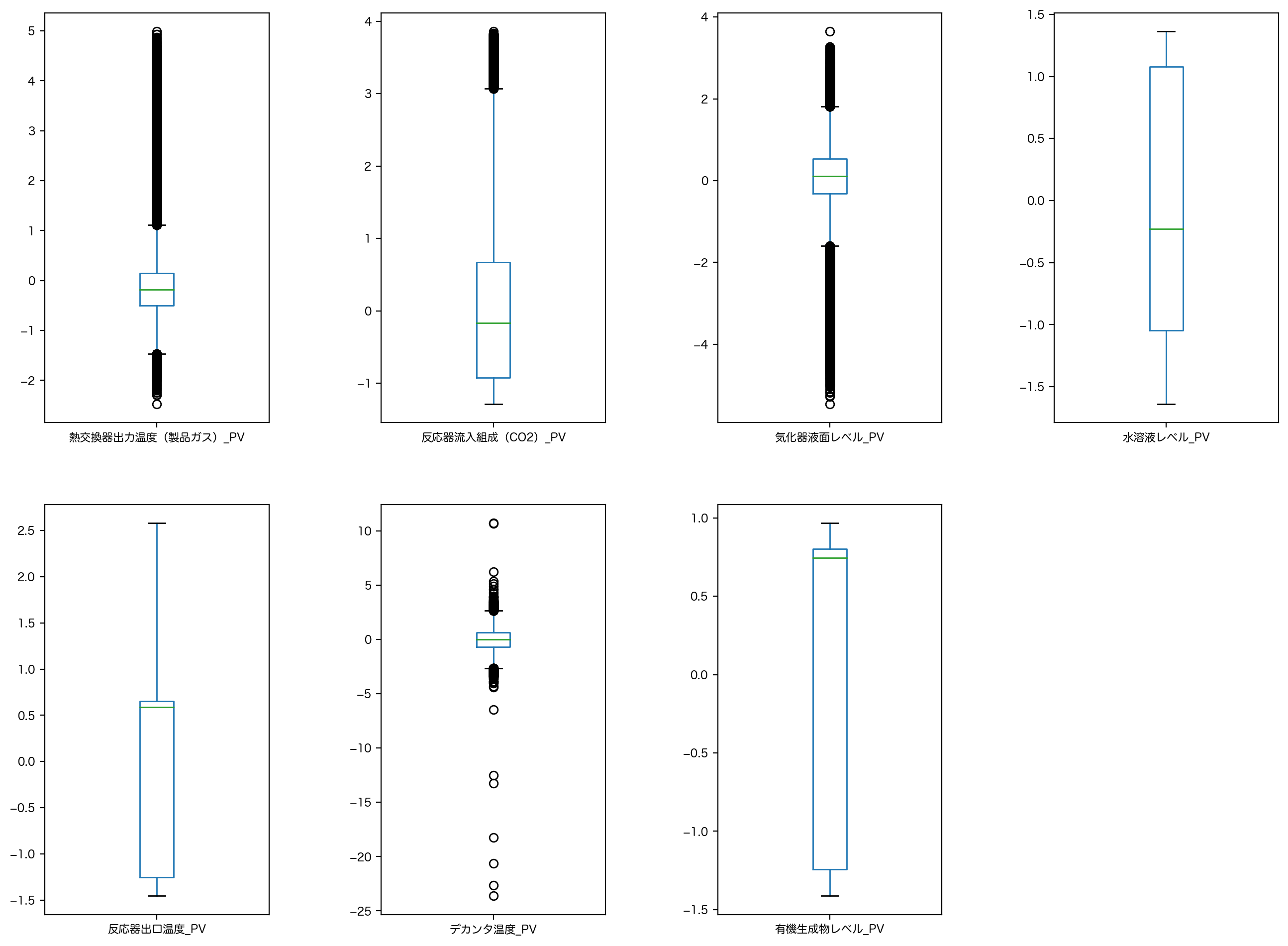
実は pandas.plot.box() では外れ値検出を行った箱ひげ図がデフォルトで出力されます。
この場合、デフォルトではヒゲの位置が最悪でも箱の両端から IQR(=75%点-25%点)×1.5 だけ離れた位置とされ、このヒゲより外側の点を外れ値と定義し図中の ◯ で表現しています。
pandas.plot.box() ではオプションで指定することで、外れ値を取り除いた箱ひげ図も確認することができます。
# 外れ値を取り除いた箱ひげ図
fig = plt.figure(figsize=[16, 12], dpi=200)
fig.subplots_adjust(wspace=0.5)
for n, column in enumerate(df.columns):
subplot = fig.add_subplot(2, 4, n+1)
df[column].plot.box(ax=subplot, showfliers=False)
plt.show()
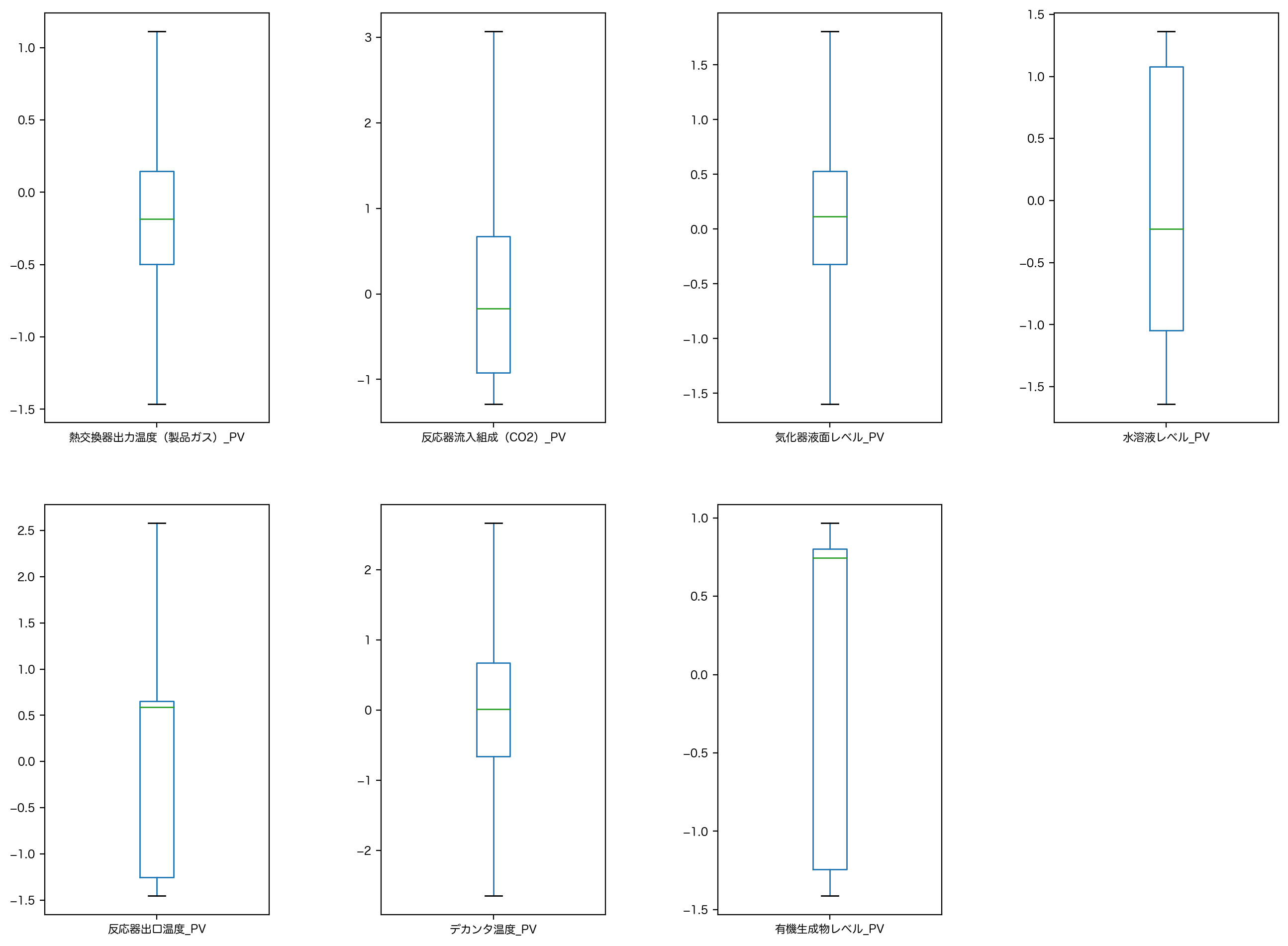
この 1.5IQR の処理の結果、元の時系列データがどのように変化するか確認してみます。
# ヒゲの取りうる範囲の限界(外れ値の閾値)を計算する
IQR = df.quantile(0.75) - df.quantile(0.25)
whiskers = pd.concat([pd.DataFrame((df.quantile(0.25) - 1.5*IQR).T, columns=['min whiskers']).T,
df.quantile([0.25, 0.75]),
pd.DataFrame((df.quantile(0.75) + 1.5*IQR).T, columns=['max whiskers']).T])
# この範囲外のデータはNaNにした後に線形補間を行った結果をプロットする。
fig = plt.figure(figsize=[8, 12], dpi=200)
fig.subplots_adjust(hspace=1.0)
for n, column in enumerate(df.columns):
subplot = fig.add_subplot(4,2,n+1)
df_tmp = df[column].copy()
df_tmp.mask((df_tmp < whiskers[column]['min whiskers']) + (whiskers[column]['max whiskers'] < df_tmp)).interpolate().plot(ax=subplot)
subplot.set_title(column)
plt.show()
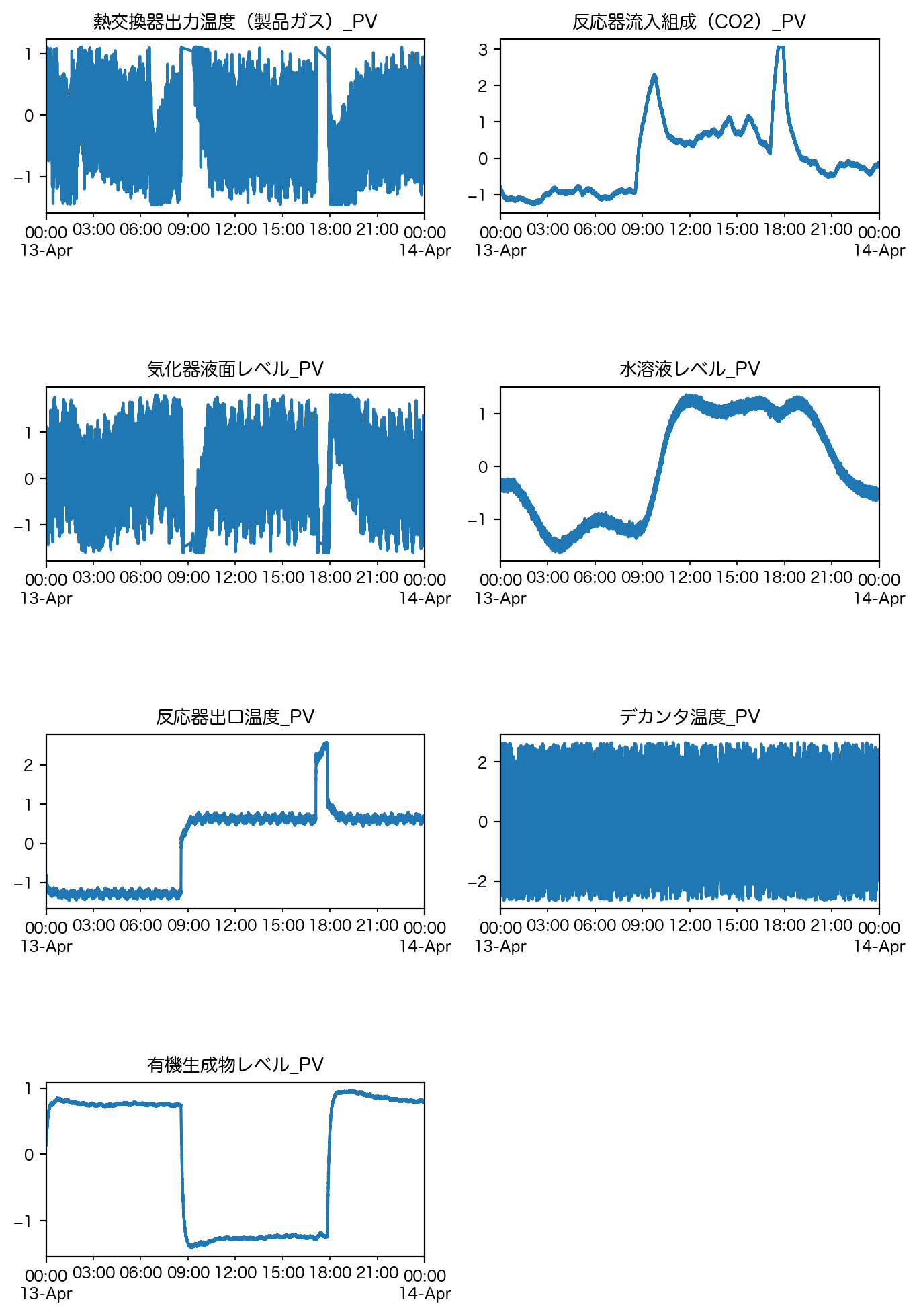
良い感じに外れ値の影響が解消されていると思います。
スミルノフ・グラブス検定#
そもそも 1.5IQR 外れ値処理をしても良いのかな、どうやってこの基準決めてんの?っという方用に、統計的に外れ値を除去する手法をいくつか紹介します。
スミルノフ・グラブス検定では外れ値処理を再帰的に行います。すなわち、最も外れた1標本のみを検定し、もし外れ値と判断されたら、それを除外した残りの標本の中の最も外れた1標本のみを検定し、…ということを外れ値が検出されなくなるまで繰り返します。
from scipy.stats import t
def SmirnovGrubbsTest(df, alpha=0.05):
df = df.reset_index(drop=True)
num, mean, std = int(df.count()), float(df.mean()), float(df.std())
t_value = t.isf(q=alpha / (2 * num), df=num - 2)
threshold = ((num - 1) * t_value) / np.sqrt(num * (num - 2) + num * t_value ** 2)
normalize = (df - mean).abs() / std
index, candidate = normalize.idxmax(), normalize.max()
return index if candidate > threshold else None
# 有意水準をここでは5%とする
alpha = 0.05
df_tmp = df.copy()
for column in df.columns:
while True:
result = SmirnovGrubbsTest(df_tmp[column], alpha=alpha)
if(result is None):
break
else:
df_tmp[column][result] = np.nan # 外れ値をNaNにする
# NaNは同様に線形補間を行いプロットする。
fig = plt.figure(figsize=[8, 12], dpi=200)
fig.subplots_adjust(hspace=1.0)
for n, column in enumerate(df.columns):
subplot = fig.add_subplot(4,2,n+1)
df_tmp[column].interpolate().plot(ax=subplot)
subplot.set_title(column)
plt.show()
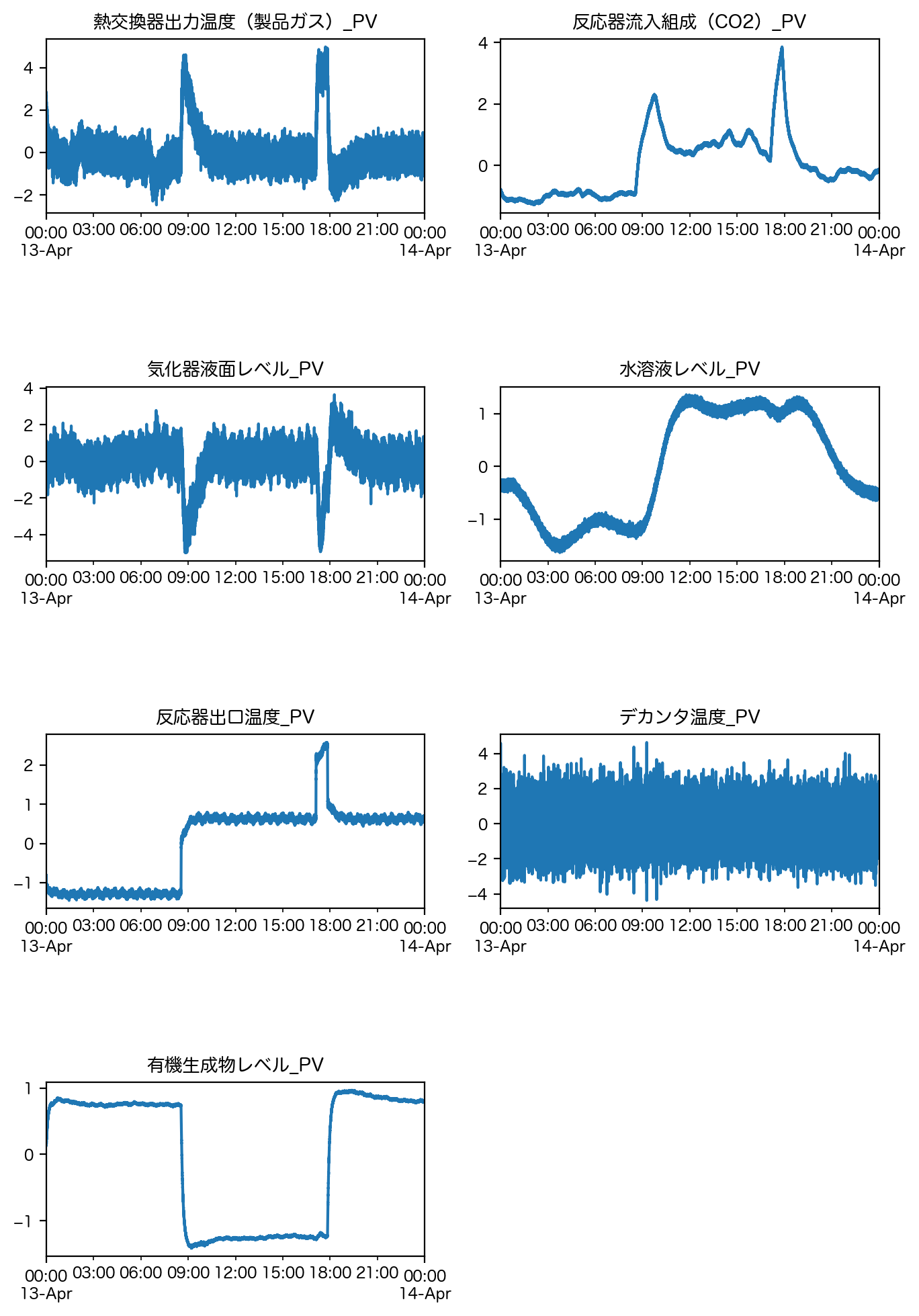
トンプソン検定#
スミルノフ・グラブス検定とは表裏一体となるアプローチで外れ値検定を行う方法にトンプソン検定があります。
この辺の統計的な詳細はほかに譲りますが、サンプル数が十分大きければスミルノフ・グラブス検定とトンプソン検定は、統計的に同じ結果になります。
from scipy.stats import t
def Thompson_Test(df, alpha=0.05):
df = df.reset_index(drop=True)
num, mean, std = int(df.count()), float(df.mean()), float(df.std())
normalize = (df - mean).abs() / std
index, candidate = normalize.idxmax(), normalize.max()
threshold = candidate * np.sqrt(num - 2) / np.sqrt(num - 1 - candidate ** 2)
t_value = t.isf(q=alpha / (2 * num), df=num - 2)
return index if threshold > t_value else None
# 有意水準をここでは5%とする
alpha = 0.05
df_tmp = df.copy()
for column in df.columns:
while True:
result = Thompson_Test(df_tmp[column], alpha = alpha)
if(result is None):
break
else:
df_tmp[column][result] = np.nan # 外れ値をNaNにする
# NaNは同様に線形補間を行いプロットする。
fig = plt.figure(figsize=[8, 12], dpi=200)
fig.subplots_adjust(hspace=1.0)
for n, column in enumerate(df.columns):
subplot = fig.add_subplot(4,2,n+1)
df_tmp[column].interpolate().plot(ax = subplot)
subplot.set_title(column)
plt.show()

小括#
本項では、外れ値処理についての基本的な手法と統計的検定手法について説明しました。
ただ、外れ値処理は思いの外奥が深く、これらを思考停止で行うよりも前に、分布型や基本統計量、およびドメイン知識などを参考に、個別具体的なデータに応じた外れ値の定義方針を決める必要があります。
例えば今回紹介した手法は、いずれもデータが正規分布に従っているという仮定を暗に置いたものです。逆に言えば、この仮定から著しく乖離している場合には、これらの手法で外れ値処理を行うと、実は超重要だった情報を自ら落としてしまうことになりかねません。
さらに言えば、データが真に正規分布に従っていたとしても、統計的に絶対正しい外れ値処理と言うものはなく、「この値が出現するのは低確率だから外れ値とみなしても良いよね」くらいのノリでしかありません。
前処理全体に言えることですが、時間の許す限り解析者のみで断定することは避け、関係者とのコミュニケーションを通じた上で、どの方針が最適かを模索することが重要だと思います。

