LiNGAMによる因果探索(基本編)#
本稿では因果分析において複数の変数(特徴量)間の線形の因果関係を表すモデルであるLinear Non-Gaussian Acyclic Model(以下LiNGAM)、およびそのパラメータ推定手法について説明します。
LiNGAMの定義#
今、\(d\)個の変数(特徴量)\(x_1, x_2, \dots, x_d\)が存在しており、それらの間に何らかの因果関係が存在するものとします。そのような因果関係が存在する変数群を表すモデルの1つがLiNGAMです。
LiNGAMでは変数\(x_1, x_2, \dots, x_d\)間の因果関係が重み付きの有向非巡回グラフ(以下DAG)で表されると仮定します。このDAGにおいて変数\(i\)から変数\(j\)への有向辺\((i, j)\)は変数\(i\)を原因(の1つ)として変数\(j\)が生じるという因果関係を意味し、このような有向辺\((i, j)\)が存在するとき変数\(i\)は変数\(j\)の親であると呼びます。また、有向辺\((i, j)\)の重み\(b_{ij}\)は因果関係の強さを表します。
そして各変数\(x_j\)はその親変数の値を辺の重み\(b_{ij}\)により重み付けした和に非正規なノイズ\(e_j\)が加わったものとします。
[1]で述べられているLiNGAMの詳細な定義は以下の通りです:
以下の3つの仮定を満たすモデルをLiNGAM(Linear Non-Gaussian Acyclic Model)と呼ぶ:
観測変数\(x_i \ (i \in \{ 1, \dots, m\})\) がある因果順序\(k(i)\)に従って並べ替え可能である。すなわち、すべての因果関係\(x_i \longrightarrow x_j\)に対して\(k(i) < k(j)\)が成立する。
各変数\(x_i\)は平均が\(0\)でかつ、因果順序において前の変数群\(\{ x_j \mid k(j)<k(i)\}\)の線形結合にノイズ\(e_i\)が加わった以下の形で表される:
\[x_i = \sum_{k(j)<k(i)}b_{ij}x_j + e_i\]
例えば上図のモデルでは\((k(1), k(2), k(3), k(4))=(2,1,3,4)\)が因果順序となります。
以上3つの仮定をおき、パラメータ推定を行うことにより因果関係を推定します。
LiNGAMの識別可能性(identifiability)#
上記の3つの仮定を満たすLiNGAMは、識別可能性(identifiability)をもちます。識別可能性とは、相異なるパラメータをもつ2つのモデルが同一の分布を生成することがないという性質です。もしLiNGAMに識別可能性がない、すなわち相異なるパラメータを持つ2つのLiNGAM A,Bが同一の分布を生成してしまう場合は、データの分布が与えられた際に真のモデルがA,Bのどちらなのか分布からだけでは判別できなくなってしまいます。LiNGAMは上記の3つの仮定が満たされている限り識別可能性を持つため、そのような真のモデルが判別できなくなる事態を回避でき、データの分布が与えられれば真のモデルを一意に推定できるようになっています。
本節ではLiNGAMの仮定、特にノイズに関する仮定が満たされない場合に真のモデルを判別できなくなるケースを具体例を交えながら見ていきます。
例1: ノイズ\(e_i\)の分布がすべて正規分布である場合#
ノイズ\(e_1, e_2\)が平均\(0\)、分散\(1\)の正規分布\(\mathcal{N}(0,1)\)に従う下のモデル(1)を考えます:
このモデル(1)では\(x_1 \rightarrow x_2\)の因果関係が存在しています。
次に、\(e_1' \sim \mathcal{N}(0,1/2), e_2' \sim \mathcal{N}(0,2)\)をノイズとする下のモデル(2)を考えてみます:
このモデル(2)では逆に\(x_2 \rightarrow x_1\)の因果関係が存在しています。
これらのモデル(1),(2)は「ノイズが正規分布に従わない」というLiNGAMの仮定を満たしていません。今、モデル(1),(2)における\((x_1, x_2)\)の結合分布を見てみると、両モデル共に平均\(\left( \begin{array}{c} 0\\0\end{array}\right)\)、共分散行列が\(\left( \begin{array}{cc} 1&1\\1&2\end{array}\right)\)の正規分布となっています。
この場合、\((x_1, x_2)\)の分布が与えられてもどちらのモデルが真のモデルなのかはデータの分布からだけではもはや識別することが不可能になってしまい、因果順序が\(x_1 \rightarrow x_2\)、\(x_2 \rightarrow x_1\)のどちらなのかも判別できなくなってしまいます。
例2: 分散\(0\)のノイズが含まれる場合#
ノイズ\(e_1\)が\([0,1]\)上の一様分布\(U[0,1]\)に従う下のモデル(3)を考えます:
次に、\(e_2' \sim U[0,2]\)をノイズとする下のモデル(4)を考えます:
これらのモデル(3),(4)は「ノイズの分散が非零である」というLiNGAMの仮定を満たしていません。今、モデル(3),(4)における\((x_1, x_2)\)の結合分布を見てみると、両モデル共に\((0,0), (1,2)\)を結ぶ線分上の一様分布となっています。この場合、例1の場合と同様にどちらのモデルが真のモデルなのかデータからだけでは識別不可能になってしまいます。
LiNGAMのパラメータ推定手法#
LiNGAMに従って生成された確率変数\(\mathbf{x}=(x_1, \dots, x_m)\)の観測値\(\mathcal{D} = \{ \mathbf{x}^{(i)} \}_{i=1}^n\)が与えられたとき、これらの観測値からモデルのパラメータ(\(k(i), b_{ij}\)など)を推定する手法にはさまざまなものがあります。代表的なものは以下の表の通りです:
手法 |
特徴 |
|---|---|
ICA-LiNGAM [1] |
独立成分分析(ICA)をベースとした手法。 |
DirectLiNGAM [2] |
外生変数を1つずつ順に除外していくことで因果順序を推定する手法。 |
以下ではDirectLiNGAMの詳細について説明します。
DirectLiNGAM#
DirectLiNGAMは2変数間の単回帰を繰り返して外生変数(因果グラフにおいて親が存在しない変数)を1つずつ順番に検出して取り除く作業を繰り返すことで、因果順序を推定する手法です。
DirectLiNGAMのアルゴリズム#
DirectLiNGAMのアルゴリズムは以下の通りです:
DirectLiNGAMのアルゴリズム
外生変数を1つ発見する。(\(x_j\)とする)
見つけた外生変数\(x_j\)が他の変数に与える影響を取り除き、その後\(x_j\)をデータから除外。
1.に戻り、同じ処理を変数がすべてなくなるまで繰り返す。
すべての変数が除外されたとき、各変数の除外された順番が因果順序そのものである。
4.で定まった因果順序をもとに、最小二乗法でDAGの重み\(b_{ij}\)を推定する。
以下では
Step 1: 外生変数の発見
Step 2: 外生変数が他の変数に与える影響の除去
の詳細を解説します。
Step 1: 外生変数の発見方法#
[2]中のLemma 1によると、以下が成り立ちます:
\(r_{ij}\)は目的変数を\(x_i\)、説明変数を\(x_j\)とした単回帰における残差、すなわち
\[ x_i = \frac{\text{Cov}[x_i, x_j]}{\text{Var}[x_j]} x_j + r_{ij} \]であるとする。 このとき\(x_j\)が外生変数であることは、任意の\(i \neq j\)について\(x_j\)と\(r_{ij}\)が独立であることと同値である。
したがって、外生変数として\(x_j\)と\(r_{ij} \ (i \neq j)\)間の独立性が最も高くなるような変数\(x_j\)を選べばよいことになります。
独立性の判定手法は多々ありますが、例えば[2]では\(x_j\)と\(r_{ij}\)の相互情報量\(MI(x_j, r_{ij})\)を利用し、以下の式(5)で定義される\(T(x_j)\)が最も小さくなる\(j\)を外生変数と判断しています:
なお、この場合数値計算では相互情報量\(MI(x_j, r_{ij})\)はカーネル法を用いて推定した値を用います。
Step 2: 外生変数が他の変数に与える影響の除去方法#
外生変数\(x_j\)を検出した後は、\(x_j\)を除外する前に\(x_j\)が他の変数に与える影響を取り除きます。そのために\(x_j\)以外の変数に対応する部分を
に置き換え、\(x_j\)が\(x_i \ (i \neq j)\)に与える影響を除去します。
なお、この操作後もLiNGAMの仮定が満たされること、および操作前後で因果順序が変化しないことは[2]のLemma 2およびCorollary 1によりそれぞれ保証されています。
実験#
最後に、lingamライブラリを用いてDirectLiNGAMによる人工データの因果探索を行います。
今回使用する人工データは下図のDAGに従うデータセットとし、ノイズ\(e_1, e_2, e_3, e_4\)はそれぞれ独立に\([-1, 1]\)上の一様分布に従うものとします。
ライブラリのインポート、関数定義#
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import networkx as nx
from lingam import DirectLiNGAM
import warnings
warnings.filterwarnings('ignore') # Warningを無視する
# ノイズX, 因果グラフGからデータセットを生成する関数
def noise_to_causal_data(X, G):
out = X.copy()
for v in nx.topological_sort(G):
for u, d in G.pred[v].items():
out[v] += d['weight'] * out[u]
return out
人工データの作成#
# 真の因果グラフGtrueの定義
Gtrue = nx.DiGraph()
Gtrue.add_nodes_from([fr'$x_{i}$' for i in range(1,5)])
Gtrue.add_weighted_edges_from([
('$x_1$', '$x_3$', -1),
('$x_2$', '$x_1$', 1),
('$x_2$', '$x_3$', 2),
('$x_2$', '$x_4$', 1)
])
e_label_dict_true = {(i, j): f'{d["weight"]:.1f}' for i, j, d in Gtrue.edges(data=True)}
e_width_list_true = [ abs(d['weight']) for (u, v, d) in Gtrue.edges(data=True)]
# 人工データセットの作成
n = 1000
np.random.seed(1)
# Xの各列に独立なノイズを入れる
X = pd.DataFrame(data=np.random.uniform(low=-1.0, high=1.0, size=(n, 4)), columns=Gtrue.nodes())
X = noise_to_causal_data(X, Gtrue)
推定&結果比較#
# 因果グラフの推定
l = DirectLiNGAM()
l.fit(X)
# 推定結果のグラフ作成
G = nx.from_numpy_array(l.adjacency_matrix_.T, create_using=nx.MultiDiGraph())
G = nx.relabel_nodes(G, {v: fr'$x_{i+1}$' for i, v in enumerate(G.nodes())})
pos = {
'$x_1$': (-1, 1),
'$x_2$': (1, 1),
'$x_3$': (-1, -1),
'$x_4$': (1, -1)
}
e_label_dict_est = {(i, j): f'{d["weight"]:.4f}' for i, j, d in G.edges(data=True)}
e_width_list_est = [ abs(d['weight']) for (u, v, d) in G.edges(data=True)]
# 推定結果の可視化
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(10, 5))
axes[0].set_title('DirectLiNGAM')
nx.draw_networkx_nodes(G, pos, ax=axes[0], node_size=1000, node_color='#ffaaaa', edgecolors='k')
nx.draw_networkx_edges(G, pos, ax=axes[0], width=e_width_list_est, style='solid', arrowstyle='->', node_size=1000, arrowsize=20)
nx.draw_networkx_labels(G, pos, ax=axes[0])
nx.draw_networkx_edge_labels(G, pos, edge_labels=e_label_dict_est, ax=axes[0], rotate=False)
axes[1].set_title('True')
nx.draw_networkx_nodes(Gtrue, pos, ax=axes[1], node_size=1000, node_color='#ffaaaa', edgecolors='k')
nx.draw_networkx_edges(Gtrue, pos, ax=axes[1], width=e_width_list_true, style='solid', arrowstyle='->', node_size=1000, arrowsize=20)
nx.draw_networkx_labels(Gtrue, pos, ax=axes[1])
nx.draw_networkx_edge_labels(Gtrue, pos, edge_labels=e_label_dict_true, ax=axes[1], rotate=False)
fig.show()
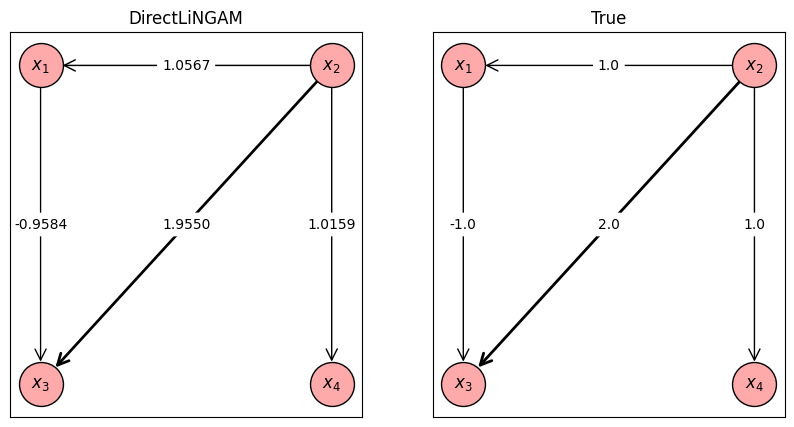
出力結果の図は左がDirectLiNGAMにより推定された因果グラフ、右が真の因果グラフです。結果を見ると、DirectLiNGAMで真の因果グラフを概ね正しく推定できていることが確認できます。
小括#
本稿では、因果探索におけるモデルの1つであるLiNGAMおよびそのパラメータ推定方法について、lingamライブラリによる実行例を交えた解説を行いました。本稿で解説したLiNGAMは因果探索のモデルの中でも基本的なものであり、線形の因果関係に限定していたり、データに含まれていない変数の影響が無いことを暗に仮定していたりなど、単純化されたモデルとなっています。
本稿はLiNGAMによる因果探索(応用編)へ続きます。応用編では総合効果の概念やDirectLiNGAMにおける前処理(標準化)の説明に加え、DirectLiNGAMの推定結果の信頼度を評価する方法を紹介します。
参考文献#
[1] A Linear Non-Gaussian Acyclic Model for Causal Discovery [Shimizu et al., 2006]

