次元圧縮（前編：主成分分析）#
※機械学習の文脈の「次元削減」や「次元圧縮」は日本語に多少ブレがあります。
ここでは高次元空間上のデータについて、
列の要素に変更は加えず、個々の列（軸）を削減することで低次元化を達成する手法を「次元削減」（VIFなど）
列の要素の変換も伴うような、何らかの写像によって低次元空間に射影する手法を「次元圧縮」（PCAなど）
と呼ぶことにします。
本項では「次元圧縮」についてまとめます。
潜在空間への招待#
次元圧縮とは、抽象的には「元の情報をできるだけ失わないような低次元部分空間を抽出する次元圧縮法」のことです。
すなわち、多次元からなる情報を、できるだけその意味（本質的情報）を保ったまま、より少ない次元の情報に落とし込みます。
潜在空間と聞くと真っ先にAutoEncoderを始めとする深層学習手法が思いつくかもしれませんが、ざっくりとした理解では同義であると考えても差し支えないです。（がしかし、深層学習手法はここでは扱いません。）
本項では、統計的に低次元部分空間を抽出する手法のうち、代表的なものをいくつかピックアップして概念的に紹介します。理論的に深入りしたい人は都度良書を手に取り数式を追いかけてみるのも良いかも知れません。特にPRML下巻は理論屋にはオススメです。
【5分でわかる次元圧縮 〜主成分分析のスキームで〜】
例えば身長と体重の関係を示したグラフとして次が与えられているとします。
このグラフにおいて、身長と体重は相関関係が強く、身長が増加するほど体重も増加し体格が良い傾向にあると捉えられます。
次元圧縮とは、集団を最もよく表現する空間上（上図の赤線）にデータを射影することで、特徴量（身長や体重など）の情報を適宜統合し、新しい指標を作ることに相当します。
その結果として、データ全体としての本質的意味を保ちつつ、次元の削減が可能となります。
すなわち良い次元圧縮とは、いかに上手く「集団を最もよく表現する」射影先の空間を求めるか？に尽きると言えるでしょう。
これに関して最も単純には、下図のように最小二乗法のようなイメージで青い線分の長さの二乗和を最小化するなどが考えられます。
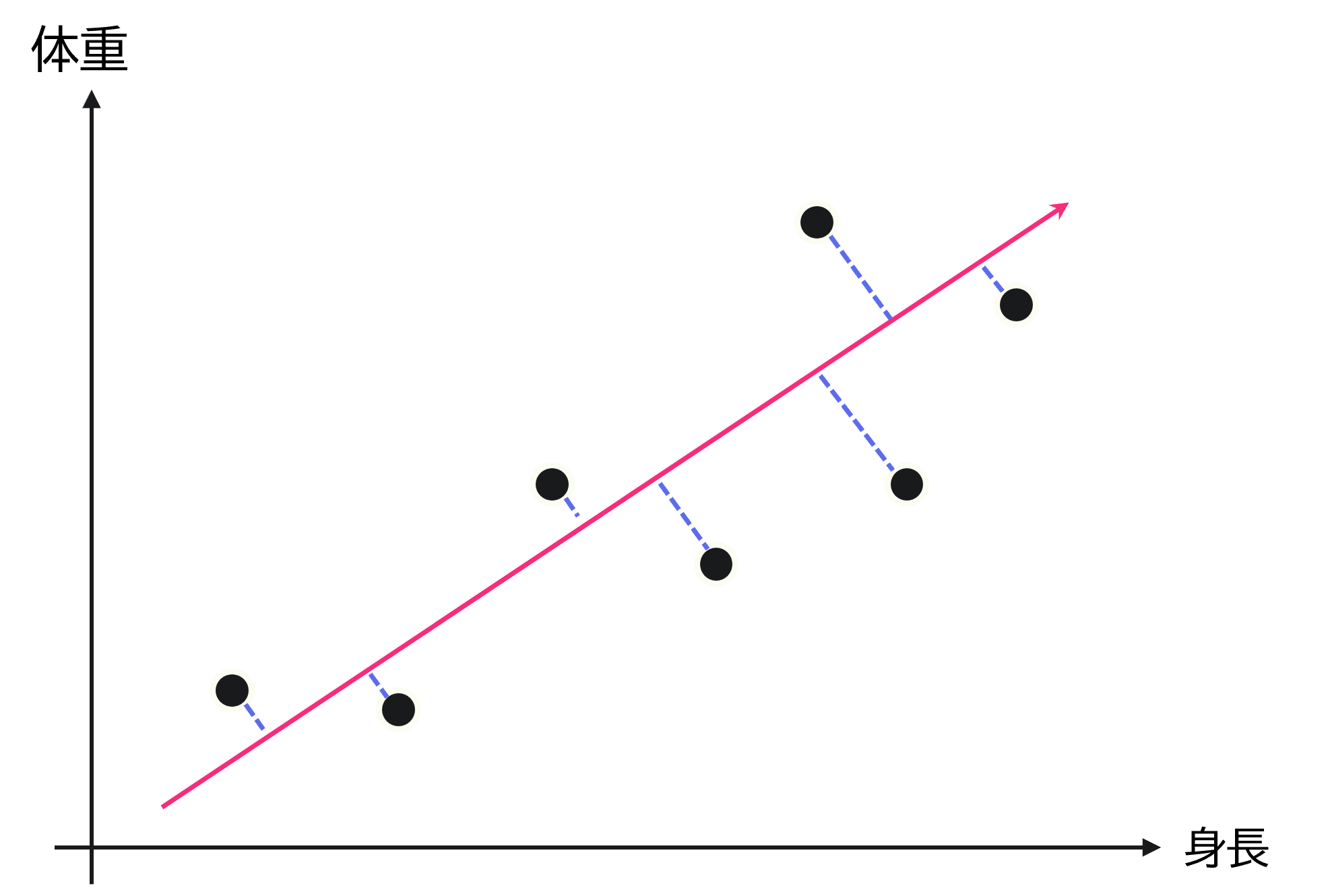
この青い線分は射影先の空間（ここでは１次元空間）と各データの間の距離を示したものです。
その長さは「射影誤差」、または青い線分の長さだけ情報が欠落するので、「情報損失量」とも呼ばれます。
この誤差・損失量が小さいほど、それぞれのデータをよく保持しているといえます。
グラフを回転させ、体重と身長の２次元情報を、図の赤い矢印で示された１次元空間に落とし込んでみた結果を表示します。
この１次元空間でも、値が増加するほど体格が良くなっている、とわかります。 今回の例は、２次元データを１次元に落とし込んでいますが、次元圧縮後も「体格を示す」というデータの意味は保てています。
次元圧縮の概念に慣れてくると、恐らく次に気になるのは「どれだけの次元数を圧縮すればいいのだろうか？」という点だと思います。
これを評価するひとつの指標に寄与率と累積寄与率があります。
第\(m\)成分の寄与率とは、射影した先の低次元空間のうち第\(m\)成分が、元のデータ全体の散らばり具合をどの程度カバーできているかを評価しています。
累積寄与率とは、各成分の寄与率を適当に累積した値が、元のデータ全体の散らばり具合をどの程度カバーできているかを評価しています。
すなわち\(\mathbb{R}^N\to\mathbb{R}^M\)なる射影を考えた場合に、累積寄与率とは\(\mathbb{R}^N\)内の元のデータの散らばりに対する、圧縮先空間\(\mathbb{R}^M\)内に射影したデータの散らばり具合の割合であり、これは1.0に近いほど元のデータの情報を保持できていることを意味します。
累積寄与率をもちいて第何主成分まで使うかを決められます。一般的な基準として、寄与率を大きい順に足し合わせていき、累積寄与率が0.8以上になる主成分を使用することが多いです。
※ \(\mathbb{R}^N\to\mathbb{R}^N\)（\(M=N\)）なる射影を考える場合は、すべての成分の寄与率についての累積寄与率は1.0となる。
例えば、次の図のような赤と緑の２つの低次元部分空間を考えるとした場合に、元のデータの射影を考えれば赤の空間の方が元のデータの散らばり具合を保持できている、すなわち情報損失の少ない良い次元圧縮であると考えられます。
３次元以上の場合も同様です。一般により低次の空間に射影すればするほど（つまり3次元⇒2次元よりも3次元⇒1次元のほうが）情報は単調に減少していきますので、寄与率・累積寄与率に基づいてどの程度まで情報損失を許容するかが重要となります。
データの読み込み#
データの読み込みに関しては次元削減で行った手法と同一です。
import warnings
warnings.filterwarnings("ignore")
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# matplotlibでは日本語にデフォルトで対応していないので、日本語対応フォントを読み込む
# plt.rcParams['font.family'] = 'BIZ UDGothic' # Windows
# plt.rcParams['font.family'] = 'Hiragino Maru Gothic Pro' # Mac
plt.rcParams["font.family"] = "Noto Sans CJK JP" # Ubuntu
# 使えるフォント一覧は以下のコードで取得できます。
# import matplotlib.font_manager
# [f.name for f in matplotlib.font_manager.fontManager.ttflist]
pd.set_option("display.max_rows", 10)
pd.set_option("display.max_columns", 10)
fpath = "../data/2020413.csv"
df = pd.read_csv(fpath, index_col=0, parse_dates=True, encoding="shift-jis")[::10]
数値型の要約統計量
df.describe()
| 気化器圧力_PV | 気化器圧力_SV | 気化器圧力_MV | 気化器液面レベル_PV | 気化器液面レベル_SV | ... | 反応器流入組成（HAc）_PV | セパレータ蒸気排出量_MV (Fixed) | アブソーバスクラブ流量_MV (Fixed) | アブソーバ還流流量_MV (Fixed) | 気化器液体流入量_MV (Fixed) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 8641.000000 | 8641.000000 | 8641.000000 | 8641.000000 | 8.641000e+03 | ... | 8641.000000 | 8.641000e+03 | 8641.000000 | 8641.000000 | 8.641000e+03 |
| mean | 128.006452 | 128.003415 | 18.739506 | 0.699816 | 7.000000e-01 | ... | 0.109533 | 1.610260e+01 | 15.119916 | 0.755890 | 2.192400e+00 |
| std | 0.732346 | 0.526849 | 0.270095 | 0.001444 | 1.110287e-16 | ... | 0.000586 | 3.552919e-15 | 0.018634 | 0.015684 | 4.441149e-16 |
| min | 125.347772 | 126.183125 | 17.867357 | 0.692315 | 7.000000e-01 | ... | 0.107120 | 1.610260e+01 | 14.119800 | 0.726000 | 2.192400e+00 |
| 25% | 127.519430 | 127.640924 | 18.558258 | 0.699342 | 7.000000e-01 | ... | 0.109155 | 1.610260e+01 | 15.119800 | 0.746000 | 2.192400e+00 |
| 50% | 128.026204 | 128.028863 | 18.737580 | 0.699988 | 7.000000e-01 | ... | 0.109522 | 1.610260e+01 | 15.119800 | 0.756000 | 2.192400e+00 |
| 75% | 128.517488 | 128.401727 | 18.920620 | 0.700583 | 7.000000e-01 | ... | 0.109899 | 1.610260e+01 | 15.119800 | 0.766000 | 2.192400e+00 |
| max | 130.392239 | 129.356617 | 19.774625 | 0.704532 | 7.000000e-01 | ... | 0.112340 | 1.610260e+01 | 16.119800 | 0.786000 | 2.192400e+00 |
8 rows × 91 columns
# 正規化を行う
from sklearn.preprocessing import StandardScaler
# 正規化を行うオブジェクトを生成
ss = StandardScaler()
# fit_transform関数は、fit関数（正規化するための前準備の計算）と
# transform関数（準備された情報から正規化の変換処理を行う）の両方を行う
df = pd.DataFrame(ss.fit_transform(df), index=df.index, columns=df.columns)
さらに分散が1.0に正規化できなかった列を取り除きます。
df = df.drop(columns=df.columns[list(df.std(axis=0) < 0.9)])
特異値分解#
【特異値分解（Singular Value Decomposition：SVD）とは】
\(m\times n\)（\(m\)行\(n\)列）の行列を分解する方法の1つで機械学習では主に次元削減に用いられる基本的な手法です。このとき行列が正方である必要はありません。
行列\(A\)（\(m\)行\(n\)列）を特異値分解すると、以下のようになります。
特に特異値分解においては以下のような性質を満たします。
\(U\)は\(m\)行\(m\)列の正方行列であり、さらに行列式が1の直交行列となる。
\(V^\mathrm{T}\)は\(n\)行\(n\)列の正方行列であり、さらに行列式が1の直交行列となる。
\(\Sigma\)は\(m\)行\(n\)列の行列で、非対角成分が0で、対角成分は非負で大きい順に並んだ行列となる。このとき\(\sigma\)を特異値という。
具体例
また特異値分解には次のような性質があります。
\(A\)が与えられたとき、特異値を定める行列\(\Sigma\)は一意に決まるが、直交行列\(U\)と\(V\)は一意に定まるとは限らない。
行列の特異値の数は、その行列のランクと一致する。
行列の特異値の二乗和はその行列の全成分の二乗和と等しくなる。
特異値分解を用いた次元圧縮は低ランク近似とも呼ばれています。具体的には以下の方針で次元圧縮を試みます。
\(A=U\Sigma V^{\mathrm{T}}\)において\(\Sigma\)は対角行列のため、対角要素\(\sigma\)（特異値）が大きければ、\(A\)に与える影響も大きくなる。
そこで\(\sigma\)（特異値）の値が小さな方から、順にいくつか0に置き換えた行列\(S\)で、\(\Sigma\)を近似できる。
低次元の行列で近似することで、次元圧縮が可能となる。
このとき復元された近似行列\(\tilde{A}\)のランクは、\(\sigma\)のうち非0として残した要素数と一致する。
また\(\tilde{A}\)は、当該ランク以下の行列全体の集合の中で、次の誤差を最小にする行列である。
from scipy.linalg import svd
# 特異値分解
# sigmaは特異値を並べたベクトルが返される
U, sigma, VT = svd(df)
近似の質を先ほどの誤差関数として定義し、 \(\sigma\) を小さな方から順に0に置き換えていくとします。このときの近似行列 \(\tilde{A}\) のランクと誤差との関係をプロットすると次のようになります。
ただし、図では横軸はランク0〜元の行列 \(A\) のランクまで、低ランクから高ランクに向かってプロットしており、縦軸はランク0のときの情報損失を100%としてスケーリングされていることに注意してください。
# sigmaを特異値行列Sigmaに変換する
Sigma = np.zeros(df.shape)
Sigma[: len(sigma), : len(sigma)] = np.diag(sigma)
loss = np.zeros(len(sigma))
for rank in range(len(sigma)):
S = np.copy(Sigma)
S[rank:, rank:] = 0
A_tilde = U @ S @ VT
loss[rank] = np.sum((A_tilde - df.values) ** 2)
loss /= np.max(loss) / 100
plt.figure(figsize=[8, 6], dpi=200)
plt.plot(loss)
plt.annotate(
r"$\mathrm{rank}\:\tilde{A}=8$",
xy=(8, loss[8]),
xycoords="data",
xytext=(+10, +30),
textcoords="offset points",
fontsize=10,
arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"),
)
plt.ylabel(r"infomation loss [%]")
plt.xlabel(r"$\mathrm{rank}\:\tilde{A}$")
plt.title(r"$A$を$\mathrm{rank}\:\tilde{A}$次元に低ランク近似した場合の情報損失")
plt.grid()
plt.show()
この図を見ると、例えば rank \(\tilde{A}=8\) は元の行列\(A\)のランク(rank=73) からみると約90%削減されている一方、情報損失は約20%に抑えられていることがわかります。
潜在意味解析#
【潜在意味解析（Latent Semantic Analysis：LSA）とは】
潜在意味解析とは特異値分解を使った次元圧縮法で別名「Truncated SVD」とも呼ばれています。基本的には主成分分析（後述）と一緒です。
大雑把に言えばTruncated、すなわち特異値を「切り捨てる」手法で、例えば単純に「特異値が10以下の場合その特異値を切り捨てる」とのイメージです。
特異値分解による低ランク近似と考え方は似通っていますが、まずは潜在意味解析のスキームで元のデータの次元を圧縮してみます。
これにより適切に次元圧縮を行えば、元のデータを表すのには十分でありつつ、あまり重要ではないデータやノイズを復元するのには不十分であるような、すなわち本質的な情報のみ抽出したデータが得られます。
from sklearn.decomposition import TruncatedSVD
# Truncated SVD
# ここでは8次元に次元圧縮を行う
dimension = 8
Truncated_svd = TruncatedSVD(n_components=dimension)
Truncated_svd.fit(df)
pd.DataFrame(
Truncated_svd.transform(df),
index=df.index,
columns=["第" + str(d + 1) + "主成分" for d in range(dimension)],
)
| 第1主成分 | 第2主成分 | 第3主成分 | 第4主成分 | 第5主成分 | 第6主成分 | 第7主成分 | 第8主成分 | |
|---|---|---|---|---|---|---|---|---|
| 2020-04-13 00:00:00 | 2.544532 | -1.148086 | -4.022454 | -0.164806 | -3.232199 | 1.364505 | -3.471160 | 1.160330 |
| 2020-04-13 00:00:10 | 3.999611 | -0.189855 | -0.152641 | 2.733245 | -3.311849 | 0.708444 | 0.627212 | 0.927164 |
| 2020-04-13 00:00:20 | 2.463849 | -0.009699 | -1.358079 | 1.838183 | -2.719946 | 0.677767 | 0.303678 | -0.048404 |
| 2020-04-13 00:00:30 | 2.730003 | 0.174351 | -1.350646 | 1.802436 | -2.552815 | 1.204961 | 0.860170 | 0.572656 |
| 2020-04-13 00:00:40 | 2.760349 | -0.347716 | -1.543944 | 0.528278 | -2.168400 | 1.697532 | -1.059566 | 1.982672 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 2020-04-13 23:59:20 | 0.887609 | -0.136067 | 3.536368 | -1.698176 | 0.171498 | -1.337971 | -0.674226 | -0.890336 |
| 2020-04-13 23:59:30 | 0.475833 | 0.302189 | 3.689156 | 0.727874 | 1.191808 | -0.942073 | 1.054133 | 0.451819 |
| 2020-04-13 23:59:40 | 0.668994 | 0.056218 | 3.676374 | -0.436557 | 0.606895 | -0.688235 | 0.685906 | -0.204630 |
| 2020-04-13 23:59:50 | 0.623432 | 0.063700 | 3.406385 | -1.655568 | 1.063966 | -0.922608 | -1.041235 | -1.033795 |
| 2020-04-14 00:00:00 | 0.581129 | 0.248680 | 3.824168 | -0.087296 | 1.075932 | 0.095761 | 0.915315 | 0.230241 |
8641 rows × 8 columns
各主成分に対する、元データの個々の列の構成情報は次のようにして確認できます。
pd.DataFrame(
Truncated_svd.components_,
index=["第" + str(d + 1) + "主成分" for d in range(dimension)],
columns=df.columns,
)
| 気化器圧力_PV | 気化器圧力_SV | 気化器圧力_MV | 気化器液面レベル_PV | 気化器液面レベル_MV | ... | 反応器流入組成（VAc）_PV | 反応器流入組成（H2O）_PV | 反応器流入組成（HAc）_PV | アブソーバスクラブ流量_MV (Fixed) | アブソーバ還流流量_MV (Fixed) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 第1主成分 | -0.007858 | -0.012501 | 0.001240 | 0.001755 | 0.181886 | ... | 0.048556 | 0.035051 | 0.026417 | 0.002982 | 0.004281 |
| 第2主成分 | -0.125162 | -0.163581 | -0.001986 | -0.149096 | -0.077472 | ... | 0.218682 | 0.211615 | -0.036228 | -0.003395 | 0.002797 |
| 第3主成分 | -0.097025 | -0.123548 | -0.004550 | -0.157659 | -0.092992 | ... | -0.189690 | -0.107972 | 0.031575 | -0.008089 | 0.009440 |
| 第4主成分 | -0.039817 | 0.051151 | 0.118315 | -0.160686 | 0.064340 | ... | 0.013558 | -0.100329 | 0.324406 | 0.001334 | 0.010771 |
| 第5主成分 | 0.261468 | 0.345637 | -0.071939 | 0.122897 | -0.011321 | ... | 0.015009 | 0.185731 | 0.041050 | 0.004712 | 0.112278 |
| 第6主成分 | -0.052659 | -0.062545 | 0.022396 | 0.001509 | -0.002710 | ... | 0.001551 | -0.030577 | -0.011569 | 0.024035 | 0.573969 |
| 第7主成分 | -0.133973 | 0.063775 | 0.589943 | 0.082411 | -0.001549 | ... | 0.007623 | 0.114687 | 0.146584 | 0.012237 | -0.009134 |
| 第8主成分 | 0.048556 | 0.045164 | 0.006384 | -0.014046 | -0.000268 | ... | 0.003426 | -0.001259 | -0.031256 | -0.010912 | -0.003682 |
8 rows × 73 columns
元データの情報全体に対する、個々の主成分が説明に寄与した割合は次のようにして確認できます。
print(
"この主成分全体の\n累積寄与率："
+ str(round(np.sum(Truncated_svd.explained_variance_ratio_), 4))
+ "\n情報損失："
+ str(round((1 - np.sum(Truncated_svd.explained_variance_ratio_)) * 100, 4))
+ "%"
)
pd.DataFrame(
Truncated_svd.explained_variance_ratio_.reshape(1, -1),
index=["寄与率"],
columns=["第" + str(d + 1) + "主成分" for d in range(dimension)],
)
この主成分全体の
累積寄与率：0.8022
情報損失：19.7766%
| 第1主成分 | 第2主成分 | 第3主成分 | 第4主成分 | 第5主成分 | 第6主成分 | 第7主成分 | 第8主成分 | |
|---|---|---|---|---|---|---|---|---|
| 寄与率 | 0.326668 | 0.180867 | 0.106031 | 0.054801 | 0.037935 | 0.036678 | 0.03194 | 0.027315 |
主成分分析#
【主成分分析（Principal Component Analysis：PCA）とは】
主成分分析については冒頭の「潜在空間への招待」で述べたので、ここでは割愛します。
掻い摘めば、相関のある高次元データから、相関がなく少数で全体のばらつきを最もよく表す低次元データへ次元圧縮することを目指します。
主成分を与える変換は、第１主成分の分散を最大化し、続く主成分はそれまでに決定した主成分と直交するという拘束条件の下で分散を最大化するようにして選ばれます。
主成分の求め方は、分散共分散行列の固有値・固有ベクトルを求める方法と、データ行列の特異値・特異ベクトルを求める方法の2種類があります。Pythonの機械学習ライブラリscikit-learnのPCA では、後者の特異値分解にもとづく方法で実装されています。
from sklearn.decomposition import PCA
# ここではn_componentsに次元数は指定しない
pca = PCA(n_components=None)
pca.fit(df)
pd.DataFrame(
pca.transform(df),
index=df.index,
columns=["第" + str(d + 1) + "主成分" for d in range(df.shape[1])],
)
| 第1主成分 | 第2主成分 | 第3主成分 | 第4主成分 | 第5主成分 | ... | 第69主成分 | 第70主成分 | 第71主成分 | 第72主成分 | 第73主成分 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2020-04-13 00:00:00 | 2.544532 | -1.148086 | -4.022453 | -0.164822 | -3.232196 | ... | -2.668136e-13 | -2.558058e-14 | 1.606196e-12 | -4.981539e-13 | 1.487549e-13 |
| 2020-04-13 00:00:10 | 3.999611 | -0.189855 | -0.152641 | 2.733228 | -3.311828 | ... | 1.313020e-13 | -1.836485e-13 | -1.924155e-12 | 1.730489e-13 | 1.059428e-14 |
| 2020-04-13 00:00:20 | 2.463849 | -0.009699 | -1.358079 | 1.838165 | -2.719920 | ... | 3.085541e-13 | 7.409386e-14 | -6.116535e-13 | -8.886825e-14 | 2.988466e-13 |
| 2020-04-13 00:00:30 | 2.730003 | 0.174351 | -1.350646 | 1.802426 | -2.552780 | ... | 5.131276e-13 | 3.352222e-13 | 5.034234e-13 | -3.910581e-13 | 5.825899e-13 |
| 2020-04-13 00:00:40 | 2.760349 | -0.347716 | -1.543944 | 0.528265 | -2.168371 | ... | 2.405040e-14 | -1.559119e-13 | -1.587827e-12 | 4.218578e-14 | 4.741622e-14 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 2020-04-13 23:59:20 | 0.887609 | -0.136067 | 3.536368 | -1.698182 | 0.171494 | ... | 3.192224e-13 | 2.413547e-13 | -2.004337e-12 | 7.399070e-14 | 4.200990e-13 |
| 2020-04-13 23:59:30 | 0.475833 | 0.302189 | 3.689156 | 0.727873 | 1.191806 | ... | -3.616096e-13 | -3.479545e-13 | -3.557941e-12 | 5.994112e-13 | -3.636469e-13 |
| 2020-04-13 23:59:40 | 0.668994 | 0.056218 | 3.676374 | -0.436564 | 0.606892 | ... | -2.598829e-13 | -2.190824e-13 | 4.080900e-13 | 1.444005e-13 | -2.671411e-13 |
| 2020-04-13 23:59:50 | 0.623432 | 0.063700 | 3.406386 | -1.655574 | 1.063978 | ... | -6.756024e-13 | -5.004250e-13 | 2.296875e-12 | 1.177352e-13 | -7.900063e-13 |
| 2020-04-14 00:00:00 | 0.581129 | 0.248680 | 3.824168 | -0.087298 | 1.075918 | ... | -1.821027e-13 | -1.884900e-13 | 1.269252e-12 | -3.647971e-14 | -1.422598e-13 |
8641 rows × 73 columns
各主成分に対する、元データの個々の列の構成情報は次のようにして確認できます。
pd.DataFrame(
pca.components_,
index=["第" + str(d + 1) + "主成分" for d in range(df.shape[1])],
columns=df.columns,
)
| 気化器圧力_PV | 気化器圧力_SV | 気化器圧力_MV | 気化器液面レベル_PV | 気化器液面レベル_MV | ... | 反応器流入組成（VAc）_PV | 反応器流入組成（H2O）_PV | 反応器流入組成（HAc）_PV | アブソーバスクラブ流量_MV (Fixed) | アブソーバ還流流量_MV (Fixed) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 第1主成分 | -0.007858 | -0.012501 | 1.239702e-03 | 1.754883e-03 | 1.818858e-01 | ... | 0.048556 | 0.035051 | 0.026417 | 2.981950e-03 | 4.281165e-03 |
| 第2主成分 | -0.125162 | -0.163581 | -1.985681e-03 | -1.490961e-01 | -7.747231e-02 | ... | 0.218682 | 0.211615 | -0.036228 | -3.394516e-03 | 2.796810e-03 |
| 第3主成分 | -0.097025 | -0.123548 | -4.550325e-03 | -1.576591e-01 | -9.299211e-02 | ... | -0.189690 | -0.107972 | 0.031575 | -8.089224e-03 | 9.439571e-03 |
| 第4主成分 | -0.039817 | 0.051151 | 1.183148e-01 | -1.606858e-01 | 6.433997e-02 | ... | 0.013559 | -0.100329 | 0.324407 | 1.333853e-03 | 1.077144e-02 |
| 第5主成分 | 0.261469 | 0.345636 | -7.193855e-02 | 1.228936e-01 | -1.132116e-02 | ... | 0.015008 | 0.185733 | 0.041049 | 4.711503e-03 | 1.122780e-01 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 第69主成分 | -0.000000 | 0.504351 | -3.055542e-14 | 4.607426e-15 | 6.937506e-14 | ... | -0.003388 | -0.005925 | -0.016094 | 1.304512e-14 | -3.499805e-15 |
| 第70主成分 | 0.000000 | -0.468352 | -4.753142e-14 | 4.524159e-15 | -1.188476e-13 | ... | -0.005966 | -0.010433 | -0.028337 | 1.093006e-14 | -2.623769e-15 |
| 第71主成分 | 0.000000 | -0.033736 | 9.000136e-14 | -1.374161e-14 | -2.208313e-13 | ... | -0.011026 | -0.019283 | -0.052375 | 2.676738e-14 | 4.174287e-14 |
| 第72主成分 | -0.000000 | -0.068877 | 2.626285e-14 | -8.205242e-16 | -2.900176e-14 | ... | 0.024781 | 0.043335 | 0.117707 | -2.101861e-14 | -5.238865e-16 |
| 第73主成分 | 0.000000 | -0.142807 | -3.149998e-14 | 9.124645e-16 | 1.133642e-13 | ... | -0.001748 | -0.003057 | -0.008303 | 1.830708e-14 | -4.750107e-15 |
73 rows × 73 columns
元データの情報全体に対する、個々の主成分が説明に寄与した割合は次のようにして確認できます。
print(
"この主成分全体の\n累積寄与率："
+ str(round(np.sum(pca.explained_variance_ratio_), 4))
+ "\n情報損失："
+ str(round((1 - np.sum(pca.explained_variance_ratio_)), 4) * 100)
+ "%"
)
pd.DataFrame(
pca.explained_variance_ratio_.reshape(1, -1),
index=["寄与率"],
columns=["第" + str(d + 1) + "主成分" for d in range(df.shape[1])],
)
この主成分全体の
累積寄与率：1.0
情報損失：0.0%
| 第1主成分 | 第2主成分 | 第3主成分 | 第4主成分 | 第5主成分 | ... | 第69主成分 | 第70主成分 | 第71主成分 | 第72主成分 | 第73主成分 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 寄与率 | 0.326668 | 0.180867 | 0.106031 | 0.054801 | 0.037935 | ... | 1.322781e-17 | 8.440755e-18 | 6.254269e-18 | 1.865530e-18 | 0.0 |
1 rows × 73 columns
plt.figure(figsize=[8, 6], dpi=200)
plt.plot(np.arange(1, df.shape[1] + 1), np.cumsum(pca.explained_variance_ratio_))
plt.annotate(
r"第8主成分までの累積寄与率",
xy=(8, np.cumsum(pca.explained_variance_ratio_)[7]),
xycoords="data",
xytext=(+10, -30),
textcoords="offset points",
fontsize=10,
arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"),
)
plt.ylabel(r"cumulative contribution ratio")
plt.xlabel(r"Principal component")
plt.title(r"ある主成分までを用いた場合の累積寄与率")
plt.grid()
plt.show()
特異値をベースに組まれた主成分分析では、次元の圧縮程度と情報損失量は、特異値分解のときと同等の結果が得られていることがわかります。
確率的主成分分析#
【確率的主成分分析（Probabilistic Principal Component Analysis：PPCA）とは】
主成分分析の重要な課題のひとつに、主成分数の選択があります。
データを低い次元に圧縮すれば扱いやすくなるが情報損失量は大きくなります。一方で圧縮する幅を少なくすれば情報の損失は抑えられるが次元はあまり圧縮されず、主成分本来の目的達成が難しくなります。
先ほどまでは、累積寄与率に基づいてこの主成分数を判断していましたが、では情報がどの程度残っていれば十分かという明確な基準は存在せず、客観的な指標とは言い切れません。
主成分分析に確率モデルを取り入れ拡張した確率的主成分分析では、情報量規準などの客観的な方法で圧縮を行う次元数を決定可能です。
さらに、以下のようなメリットもあります。
得られた尤度関数から、AICなどの情報量規準を用いて、主成分軸の数を客観的に決めることができる。
EMアルゴリズムを用いることで、データに欠損値があるときでも分析ができる。
高次元データの構造を次元圧縮してクラスタリング（分類）に利用できる。
すなわち、確率モデルを取り入れたことで尤度関数を得ることができ、最尤法を用いてパラメータの最尤推定量を求められます。
この結果、AICやBICといった情報量規準などを用いて、圧縮を行う次元数を決定できます。
scikit-learnではPCAのオプションで PCA(n_components = 'mle') 指定することで、Thomas P. Minka (2000) の方法で自動的に最適な主成分数を決定してくれます。
スパース主成分分析#
【スパース主成分分析（Sparse Principal Component Analysis：SparsePCA）とは】
主成分分析で実際の案件を解析する場合、変換した主成分全体のうち最初の（寄与率の高い）数個を取り出して、分析結果を視覚的に確認して解釈を与えようとすることが多いと思います。
例えば主成分軸についてデータの散布図をプロットする場合、最初の２、３個の主成分を選んで、解釈を試みることがほとんどです（通常人間は高々３次元程度しか空間を捉えられないから仕方ない）。
しかし、これらの主成分ベクトルが、複雑な変換によって構成されている場合、個々の主成分軸が何を意味するのか直感的に解釈できないことがよくあります。
冒頭の例では、身長と体重は相関関係が強く、身長が増加するほど体重も増加するようなデータの主成分軸は、身長と体重を適当な比率で和を取った「体格」という新しい軸では？と解釈できました。
しかし、解析対象の列数が多くなってくると、一般に主成分ベクトルは複雑な比率で入り乱れるため、なかなか的を得た意味付けが困難です。
この課題を解決する手法のひとつがスパース主成分分析です。
スパース主成分分析では、主成分を推定する際にスパース推定の技術を用いて、本質的ではない主成分ベクトルの要素がなるべく0になるように罰則を設けます。
これにより通常の主成分分析よりも寄与率・累積寄与率は若干悪化するものの、人間が直感的に理解しやすい主成分軸を得られます。
from sklearn.decomposition import SparsePCA
from sklearn.preprocessing import normalize
# multiprocessingにおいてWarningが発生するため抑制
import warnings
warnings.filterwarnings("ignore", category=UserWarning, module="pkg_resources")
# ここではn_componentsに次元数は指定しない
sparse_pca = SparsePCA(alpha=0.1, n_components=None, n_jobs=-1)
sparse_pca.fit(df)
# 手動で主成分を正規化
normalized_components = normalize(sparse_pca.components_, norm="l2", axis=1)
# SparsePCAは寄与率計算のメソッドがなさそうなので手計算
sparse_pca_explained_variance_ratio_ = np.sum(
sparse_pca.transform(df) ** 2, axis=0
) / np.sum(df.values**2)
sort_index = list(np.argsort(-sparse_pca_explained_variance_ratio_))
sparse_pca_explained_variance_ratio_ = sparse_pca_explained_variance_ratio_[sort_index]
pd.DataFrame(
sparse_pca.transform(df)[:, sort_index],
index=df.index,
columns=["第" + str(d + 1) + "主成分" for d in range(df.shape[1])],
)
| 第1主成分 | 第2主成分 | 第3主成分 | 第4主成分 | 第5主成分 | ... | 第69主成分 | 第70主成分 | 第71主成分 | 第72主成分 | 第73主成分 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2020-04-13 00:00:00 | 0.136227 | -0.322936 | 0.911138 | -0.177528 | 0.435005 | ... | 0.115336 | 0.717496 | -2.719936 | -0.337551 | -0.083117 |
| 2020-04-13 00:00:10 | 0.236421 | -0.189800 | -0.177060 | -0.240114 | 0.192854 | ... | 0.088214 | 0.642674 | -2.281433 | 0.013103 | 0.067547 |
| 2020-04-13 00:00:20 | 0.445950 | -0.544064 | -1.314729 | -0.318553 | 0.192346 | ... | 0.027579 | 0.719805 | -1.682211 | 0.019845 | 0.060942 |
| 2020-04-13 00:00:30 | 0.532756 | -0.328960 | -0.617953 | -0.344186 | 0.195944 | ... | 0.000031 | 0.901965 | -1.277887 | -0.000827 | 0.132173 |
| 2020-04-13 00:00:40 | 0.633305 | -0.061495 | 0.623292 | -0.335750 | 0.210481 | ... | 0.079582 | 0.842170 | -1.079314 | -0.003291 | 0.041627 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 2020-04-13 23:59:20 | -0.253682 | -0.525497 | -0.767847 | 0.830121 | 1.074659 | ... | -0.352391 | -0.249241 | 0.151591 | -0.199730 | -0.223206 |
| 2020-04-13 23:59:30 | 0.048305 | -0.517570 | 0.749582 | 0.802526 | 1.070509 | ... | -0.330394 | -0.212016 | 0.214402 | -0.207729 | -0.018709 |
| 2020-04-13 23:59:40 | 0.161118 | -0.548447 | -0.224789 | 0.797900 | 1.074962 | ... | -0.351618 | -0.350678 | 0.254785 | -0.214574 | -0.147603 |
| 2020-04-13 23:59:50 | 0.092196 | -0.301873 | -0.883384 | 0.809887 | 1.070766 | ... | -0.577057 | -0.409366 | 0.313601 | -0.215529 | -0.111083 |
| 2020-04-14 00:00:00 | -0.173440 | -0.322317 | 0.369328 | 0.818643 | 1.070225 | ... | -0.279558 | -0.242466 | 0.173153 | -0.210241 | -0.055948 |
8641 rows × 73 columns
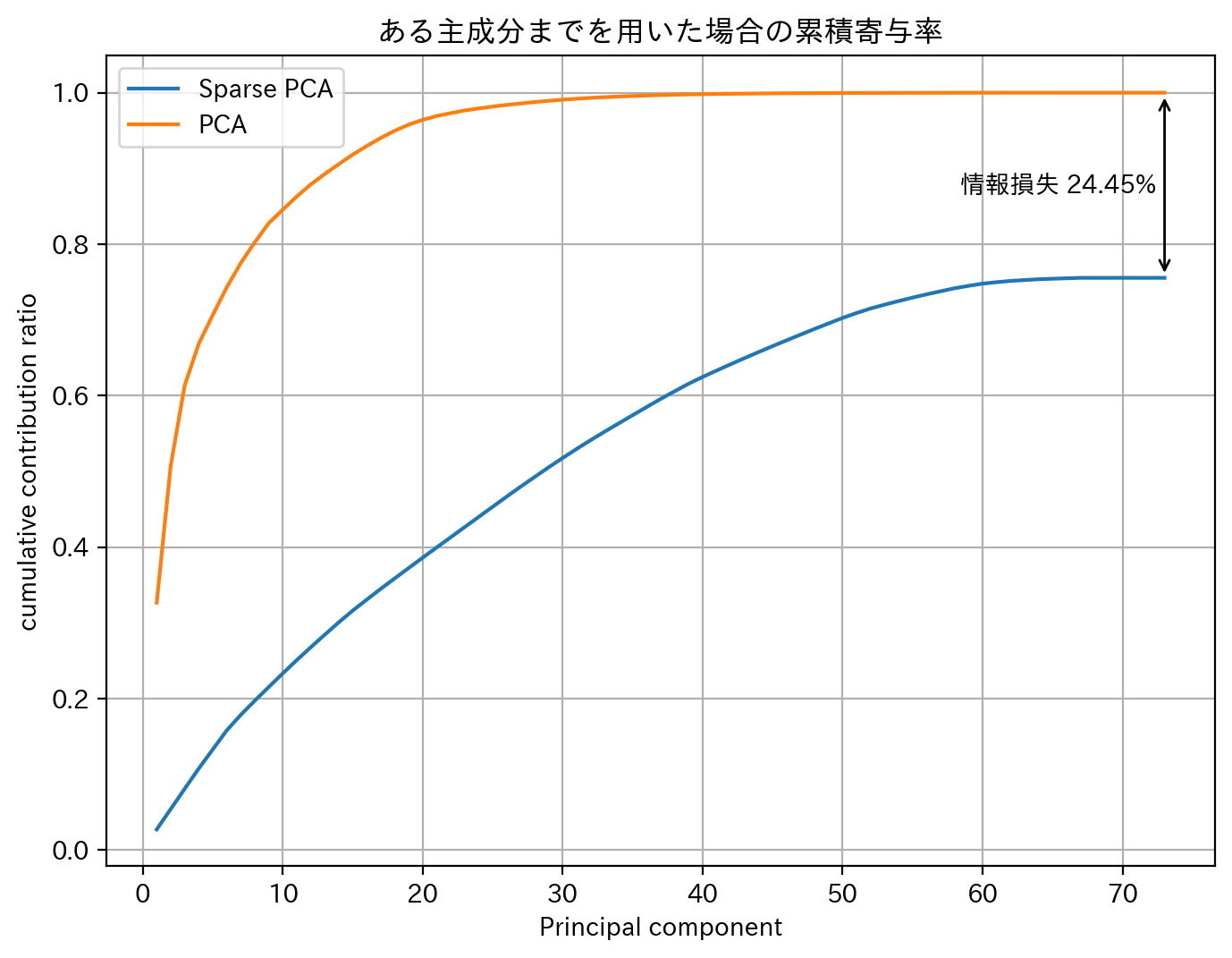
スパース主成分分析と通常の主成分分析の累積寄与度を比較すると、スパース主成分分析は幾分か情報損失を起こしていることがわかります。
plt.figure(figsize=[8, 6], dpi=200)
plt.plot(
np.arange(1, df.shape[1] + 1),
np.cumsum(sparse_pca_explained_variance_ratio_),
label="Sparse PCA",
)
plt.plot(
np.arange(1, df.shape[1] + 1), np.cumsum(pca.explained_variance_ratio_), label="PCA"
)
plt.annotate(
"",
xy=(len(pca.explained_variance_ratio_), np.sum(pca.explained_variance_ratio_)),
xycoords="data",
xytext=(
len(sparse_pca_explained_variance_ratio_),
np.sum(sparse_pca_explained_variance_ratio_),
),
arrowprops=dict(arrowstyle="<->"),
)
plt.text(
len(pca.explained_variance_ratio_) * 0.8,
(
np.sum(pca.explained_variance_ratio_)
+ np.sum(sparse_pca_explained_variance_ratio_)
)
/ 2,
"情報損失 {}%".format(
np.round(
(
1
- np.sum(sparse_pca_explained_variance_ratio_)
/ np.sum(pca.explained_variance_ratio_)
)
* 100,
2,
)
),
va="center",
ha="left",
rotation=0,
)
plt.legend()
plt.ylabel(r"cumulative contribution ratio")
plt.xlabel(r"Principal component")
plt.title(r"ある主成分までを用いた場合の累積寄与率")
plt.grid()
plt.show()
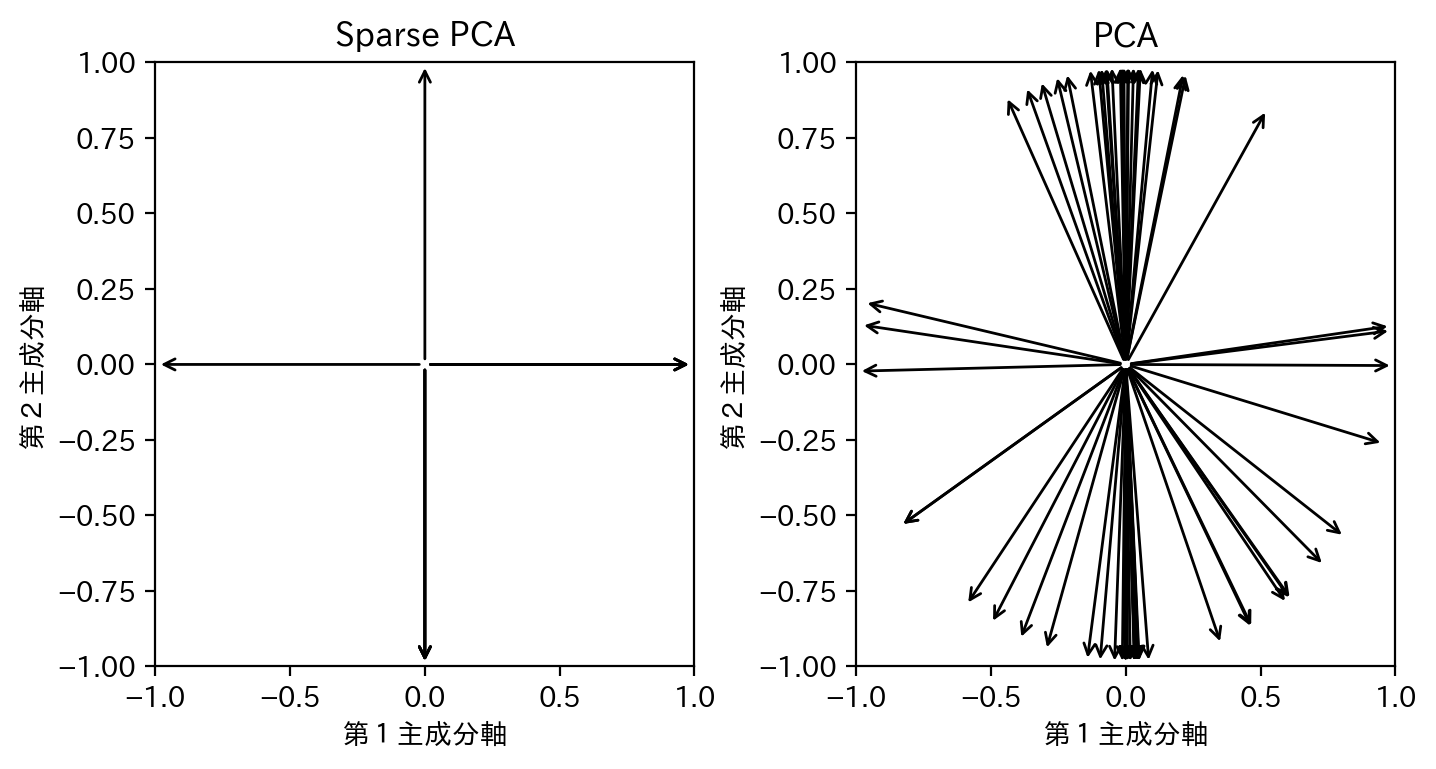
その一方で、第１主成分軸第２主成分軸平面からみた、元のデータの軸方向（適当に長さ１に正規化したもの）を図示してみると、スパース主成分分析のメリットが読み取れます。
すなわち、スパース主成分分析では、ほとんどの元のデータの軸が主成分軸（第３主成分軸以降と重なっている場合はこの図では明示的に図示されないことに注意）と重なっています。通常の主成分分析ではこのような変換は全く意識されないので、一般的には主成分軸と元のデータの軸が重なりません。
このことからも、スパース主成分分析では、主成分軸は元のデータの軸を可能な限りシンプルな比率で線型結合したもの、つまり線型結合の係数がスパースになるような変換となっていると理解できるでしょう。
fig = plt.figure(figsize=[8, 4], dpi=200)
fig.subplots_adjust(wspace=0.3)
ax_sparse_pca = fig.add_subplot(1, 2, 1)
ax_sparse_pca.set_xlim(-1, 1)
ax_sparse_pca.set_ylim(-1, 1)
ax_sparse_pca.set_xlabel("第１主成分軸")
ax_sparse_pca.set_ylabel("第２主成分軸")
ax_sparse_pca.set_title("Sparse PCA")
# 正規化された主成分をプロット
for n, to in enumerate(normalized_components[sort_index][:2].T):
if np.linalg.norm(to) != 0:
to = to / np.linalg.norm(to)
ax_sparse_pca.annotate(
"", xy=(0, 0), xytext=to, xycoords="data", arrowprops=dict(arrowstyle="<-")
)
ax_pca = fig.add_subplot(1, 2, 2)
ax_pca.set_xlim(-1, 1)
ax_pca.set_ylim(-1, 1)
ax_pca.set_xlabel("第１主成分軸")
ax_pca.set_ylabel("第２主成分軸")
ax_pca.set_title("PCA")
for n, to in enumerate(pca.components_[sort_index][:2].T):
to = to / np.linalg.norm(to)
ax_pca.annotate(
"", xy=(0, 0), xytext=to, xycoords="data", arrowprops=dict(arrowstyle="<-")
)
plt.show()
カーネル主成分分析#
【カーネル主成分分析（Kernel Principal Component Analysis：KernelPCA）とは】
いわゆる非線形なデータに通常の主成分分析を適用しても、多くの場合は上手く次元を圧縮できません。
というのも主成分分析では、データを分散が最大になるように線形的に写像し主成分を選択しています。
このような場合、カーネル法でデータを非線形変換した後に主成分分析を行う、カーネル主成分分析を実施すれば、通常の主成分分析よりもうまく次元圧縮ができます。
カーネル法についての詳細は別の機会に譲りますが、通常の主成分分析と対比しつつまとめると、以下のようになります。
主成分分析は共分散行列の固有値問題に帰着する
カーネル主成分分析はグラム行列の固有値問題に帰着する
実はどちらも計画行列の特異値分解を（それぞれ別の方面から）解いていることに相当する
ここでは図示の簡単化のため、気化器圧力_PVとリサイクルガス組成（O2）_PVの２つのカラムのみを用います。
plt.figure(figsize=[8, 6], dpi=200)
plt.scatter(df["気化器圧力_PV"], df["リサイクルガス組成（O2）_PV"])
plt.xlim(-4, 4)
plt.ylim(-4, 4)
plt.xlabel("気化器圧力_PV")
plt.ylabel("リサイクルガス組成（O2）_PV")
plt.show()
カーネル主成分分析では、（グラム行列を用いて主成分分析を行うため）空間の次元数はサンプルの数になります（通常の主成分分析のように列の数ではないことに注意）。
ここではカーネル主成分分析の主成分軸について第４主成分まで変換してみます。
scikit-learnのKernelPCA をもちいます。kernel オプションを指定することで、“linear”、“poly”、“rbf”、“sigmoid”、“cosine”、“precomputed”からどのような非線形変換を考えるか選択できます（デフォルトは”linear”に注意）。一般的な解析では、“rbf” カーネルを指定する場合が多いです。
from sklearn.decomposition import KernelPCA
# ここではn_components=4とする
kernel_pca = KernelPCA(n_components=4, kernel="rbf", n_jobs=-1)
kernel_pca.fit(df[["気化器圧力_PV", "リサイクルガス組成（O2）_PV"]])
pd.DataFrame(
kernel_pca.transform(df[["気化器圧力_PV", "リサイクルガス組成（O2）_PV"]]),
index=df.index,
columns=["第" + str(d + 1) + "主成分" for d in range(4)],
)
| 第1主成分 | 第2主成分 | 第3主成分 | 第4主成分 | |
|---|---|---|---|---|
| 2020-04-13 00:00:00 | 0.539664 | 0.385299 | -0.056207 | -0.318202 |
| 2020-04-13 00:00:10 | 0.341896 | 0.588727 | 0.023554 | -0.365673 |
| 2020-04-13 00:00:20 | 0.583803 | 0.341060 | -0.009250 | -0.280022 |
| 2020-04-13 00:00:30 | 0.357462 | 0.564629 | -0.030131 | -0.362641 |
| 2020-04-13 00:00:40 | 0.601921 | 0.225704 | -0.093213 | -0.184865 |
| ... | ... | ... | ... | ... |
| 2020-04-13 23:59:20 | -0.063470 | -0.571869 | -0.127304 | -0.118839 |
| 2020-04-13 23:59:30 | -0.429215 | 0.468213 | 0.108066 | 0.516263 |
| 2020-04-13 23:59:40 | 0.057407 | -0.616005 | -0.030408 | -0.016262 |
| 2020-04-13 23:59:50 | -0.217000 | -0.427218 | -0.270806 | -0.180643 |
| 2020-04-14 00:00:00 | -0.500451 | 0.443980 | -0.005444 | 0.439151 |
8641 rows × 4 columns
通常の主成分分析も改めてやってみます（今回は２列なので、主成分軸も第２成分までしか抽出されないことに注意）。
from sklearn.decomposition import PCA
pca_ = PCA(n_components=None)
pca_.fit(df[["気化器圧力_PV", "リサイクルガス組成（O2）_PV"]])
pd.DataFrame(
pca_.transform(df[["気化器圧力_PV", "リサイクルガス組成（O2）_PV"]]),
index=df.index,
columns=["第" + str(d + 1) + "主成分" for d in range(2)],
)
| 第1主成分 | 第2主成分 | |
|---|---|---|
| 2020-04-13 00:00:00 | -0.823748 | -0.868469 |
| 2020-04-13 00:00:10 | -0.394948 | -1.297883 |
| 2020-04-13 00:00:20 | -0.967240 | -0.816175 |
| 2020-04-13 00:00:30 | -0.419698 | -1.197442 |
| 2020-04-13 00:00:40 | -0.971827 | -0.598715 |
| ... | ... | ... |
| 2020-04-13 23:59:20 | -0.085852 | 0.806139 |
| 2020-04-13 23:59:30 | 1.485776 | -0.750827 |
| 2020-04-13 23:59:40 | -0.286847 | 0.947635 |
| 2020-04-13 23:59:50 | 0.147699 | 0.560238 |
| 2020-04-14 00:00:00 | 1.293106 | -0.558507 |
8641 rows × 2 columns
カーネル主成分分析と通常の主成分分析について、軸方向を図示してみます。
ただし、カーネル主成分分析では主成分軸も非線形になるため主成分値の等高線を、通常の主成分分析は主成分の軸正方向を図示していることに注意してください。
X = np.linspace(-4, 4, 100)
Y = np.linspace(-4, 4, 100)
X, Y = np.meshgrid(X, Y)
Z = kernel_pca.transform(np.c_[X.flatten(), Y.flatten()])
fig = plt.figure(figsize=[16, 12], dpi=200)
for n in range(4):
subplot = fig.add_subplot(2, 2, n + 1)
subplot.set_xlim(-4, 4)
subplot.set_ylim(-4, 4)
subplot.set_xlabel("気化器圧力_PV")
subplot.set_ylabel("リサイクルガス組成（O2）_PV")
subplot.set_title("第{}主成分".format(n + 1))
subplot.contour(X, Y, Z[:, n].reshape(100, 100), 30)
subplot.scatter(df["気化器圧力_PV"], df["リサイクルガス組成（O2）_PV"])
if n < 2:
subplot.annotate(
"",
xy=(0, 0),
xytext=pca_.components_[n] * 4,
xycoords="data",
arrowprops=dict(arrowstyle="<-"),
)
plt.show()
カーネル主成分分析では、非線形な変換を行い、データに内在する非線形な変化を捉えられます。
例えば、第４主成分などをみると、左右に間延びした少し集団から離れたデータについても、これらを適確に捉えた主成分軸を非線形に抽出できています。
小括#
前編では主に主成分分析系統の次元圧縮手法についてまとめました。後編に続きます！
参考文献#
前処理大全 第8章 数値型 8-6 主成分分析による次元圧縮
パターン認識と機械学習（下） 第12章 連続潜在変数
