Hilbert-Schmidt独立性基準(HSIC)#
はじめに#
2つの変数間の依存関係を測りたいとき、誰もがまっさきに思いつく方法は相関係数を計算することだと思います。
相関係数の計算方法については基本的な要約統計量の計算を参照してみてください。
ところで、この相関係数ですが、変数間の線形な関係しか捉えることができないという重大な問題があります。
例えばWikipediaから引用の次の図をご覧ください。

ここではさまざまな2次元データ\((x,y)\)と、それに基づいて計算される相関係数の例が示されています。
これを見ると、相関係数はデータの線形関係に注目して、その正負の向きとばらつきを反映しますが(上段)、その関係の傾き自体や(中段)、ほとんどすべての非線形関係も反映することはできません(下段)。
(中央の図の傾きは0ですが、この場合は\(Y\)の分散が0であるため相関係数は定義できません。)
実際、相関係数が\(\pm1\)の値をとるのは、2つの確率変数が完全に線形な関係にあるとき、かつそのときに限ることが知られています。
また2つの確率変数が互いに独立ならば相関係数は0となるものの、その逆は成り立たないことも知られています。
相関係数はこのような非常に単調な関係性しか評価できないということは、実用上も常に心に留めておく必要があります。
そこで本稿では、特に非線形な関係を取り扱う指標としてHilbert-Schmidt独立性基準(HSIC)を用いた検定について紹介します。
HSICは2変数\(X\)と\(Y\)の間の独立性を評価するノンパラメトリックな指標で、より値が0に近いほど2変数は独立であると言うことができます。
イメージとしては、複雑な非線形関係にある\(X\)と\(Y\)も、何かとっても都合の良い写像で飛ばした先では単純な関係であり、独立性も簡単に評価できるんじゃないかという想いから来ています。
機械学習のカーネル法などに詳しい方は、そのイメージで十分です!
この先、深入りすると理論面は非常に煩雑で困難を極めますので、本稿では付録としてHSICの導出を掲載するに留めさせてください。
ですが非常に有用な指標ですので、ぜひ手を動かしてHSICの面白さを体感いただければと思います。
HSICによる独立性検定の実装#
本稿では次の実装済みコードを用いてHSICによる独立性検定を行います。
コードの細かな詳細は割愛し、ここでは関数の入出力関係についての紹介のみとさせていただければと思います。
入力:
X (np.ndarray): 第1変数 (n_samples, n_features)
Y (np.ndarray): 第2変数 (n_samples, n_features)
alpha (float): 検定の有意水準 (0<alpha<1)
出力:
なおコードは実装者によって動作確認済みですが、不安で信用ならない方、さらなる詳細を知りたい方は参考文献記載のA Kernel Statistical Test of Independenceなども参照いただければと思います。
import numpy as np
import scipy.stats as st
from sklearn.gaussian_process import kernels
def HSIC_test(X: np.ndarray, Y: np.ndarray, alpha: float = 0.5) -> (bool, float, float, float):
""" HSIC test
【参考文献】
- https://proceedings.neurips.cc/paper/2007/file/d5cfead94f5350c12c322b5b664544c1-Paper.pdf
- https://github.com/amber0309/HSIC
【Memo】
- RBFカーネルのスケールはデータから自動調整
Args:
X (np.ndarray): 第1変数 (n_samples, n_features)
Y (np.ndarray): 第2変数 (n_samples, n_features)
alpha (float): 検定の有意水準 (0<alpha<1)
Returns:
H0Reject (bool): 帰無仮説は棄却されるか?
- False: 帰無仮説は棄却されない(XとYは独立ではないといえない)
- True: 帰無仮説は棄却される(XとYは独立ではない)
testStat (float): 検定統計量
thresh (float): 有意水準にもとづく閾値(検定統計量以下なら棄却)
pvalue (float): 検定統計量にもとづくp値(有意水準以下なら棄却)
"""
def auto_width(data):
G = np.sum(data**2, axis=1).reshape(-1,1)
dists = np.tile(G, (1, N)) + np.tile(G.T, (N, 1)) - 2*data@data.T
dists = np.tril(dists, k=-1).flatten()
width = np.sqrt(0.5*np.median(dists[dists>0]))
return width
if np.ndim(X) == 1:
X = X.reshape(-1,1)
if np.ndim(Y) == 1:
Y = Y.reshape(-1,1)
if X.shape != Y.shape:
raise ValueError(f'X and Y must have the same shape. : {X.shape}!={Y.shape}')
if (alpha<=0)or(1<=alpha):
raise ValueError(f'Parameter alpha must be in open interval (0,1).')
N, P = X.shape
# Auto-selected width
width_x = auto_width(X)
width_y = auto_width(Y)
# Gram matrix
K = kernels.RBF(length_scale=width_x).__call__(X, X)
L = kernels.RBF(length_scale=width_y).__call__(Y, Y)
# Centralized Gram matrix
Q = np.identity(N) - np.ones([N,N]) / N
Kc = Q @ K @ Q
Lc = Q @ L @ Q
# Test statistic
testStat = np.sum(Kc.T*Lc) / N
# variance HSIC
varHSIC = (Kc*Lc)**2
varHSIC = (np.sum(varHSIC)-np.trace(varHSIC)) / (N*(N-1))
varHSIC = (varHSIC*2*(N-4)*(N-5)) / (N*(N-1)*(N-2)*(N-3))
# mean HSIC
muX = np.sum(K*~np.identity(N).astype(bool)) / (N*(N-1))
muY = np.sum(L*~np.identity(N).astype(bool)) / (N*(N-1))
mHSIC = ((muX-1)*(muY-1)) / N
# shape parameter and scale parameter
a = mHSIC**2 / varHSIC
scale = varHSIC*N / mHSIC
# thresh, pvalue, reject H0?
thresh = st.gamma.isf(alpha, a, scale=scale)
pvalue = st.gamma.sf(testStat, a, scale=scale)
H0Reject = testStat > thresh
return H0Reject, testStat, thresh, pvalue
使ってみよう!#
ではさっそく、相関係数では関係性の抽出が困難ないくつかのデータを用いて、HSICによる独立性検定の結果を比較してみようと思います。
なお、ここでは有意水準は常に0.05としています。
読み込み#
import numpy as np
import scipy.stats as st
import matplotlib.pyplot as plt
import seaborn as sns
np.random.seed(1)
二次関数#
N = 1000
X = np.random.uniform(-2,2,size=[N,1])
Y = X**2 + np.random.normal(size=[N,1])
X_normalized = st.zscore(X)
Y_normalized = st.zscore(Y)
plt.figure(figsize=[8,6], dpi=200)
plt.scatter(X_normalized, Y_normalized)
plt.xlabel('(Normalized) X')
plt.ylabel('(Normalized) Y')
plt.grid()
plt.show()

print(f'相関係数: {round(np.corrcoef(X_normalized.flatten(),Y_normalized.flatten())[0,1], 3)}')
相関係数: -0.014
H0Reject, testStat, thresh, pvalue = HSIC_test(X, Y, alpha = 0.05)
print(f'帰無仮説は棄却されるか?: {H0Reject}')
print(f'P値: {pvalue}')
帰無仮説は棄却されるか?: True
P値: 1.0122301991832691e-103
四次関数#
N = 1000
X = np.random.uniform(-2,2,size=[N,1])
Y = X**4 - 4*X**2 + np.random.normal(size=[N,1])
X_normalized = st.zscore(X)
Y_normalized = st.zscore(Y)
plt.figure(figsize=[8,6], dpi=200)
plt.scatter(X_normalized, Y_normalized)
plt.xlabel('(Normalized) X')
plt.ylabel('(Normalized) Y')
plt.grid()
plt.show()
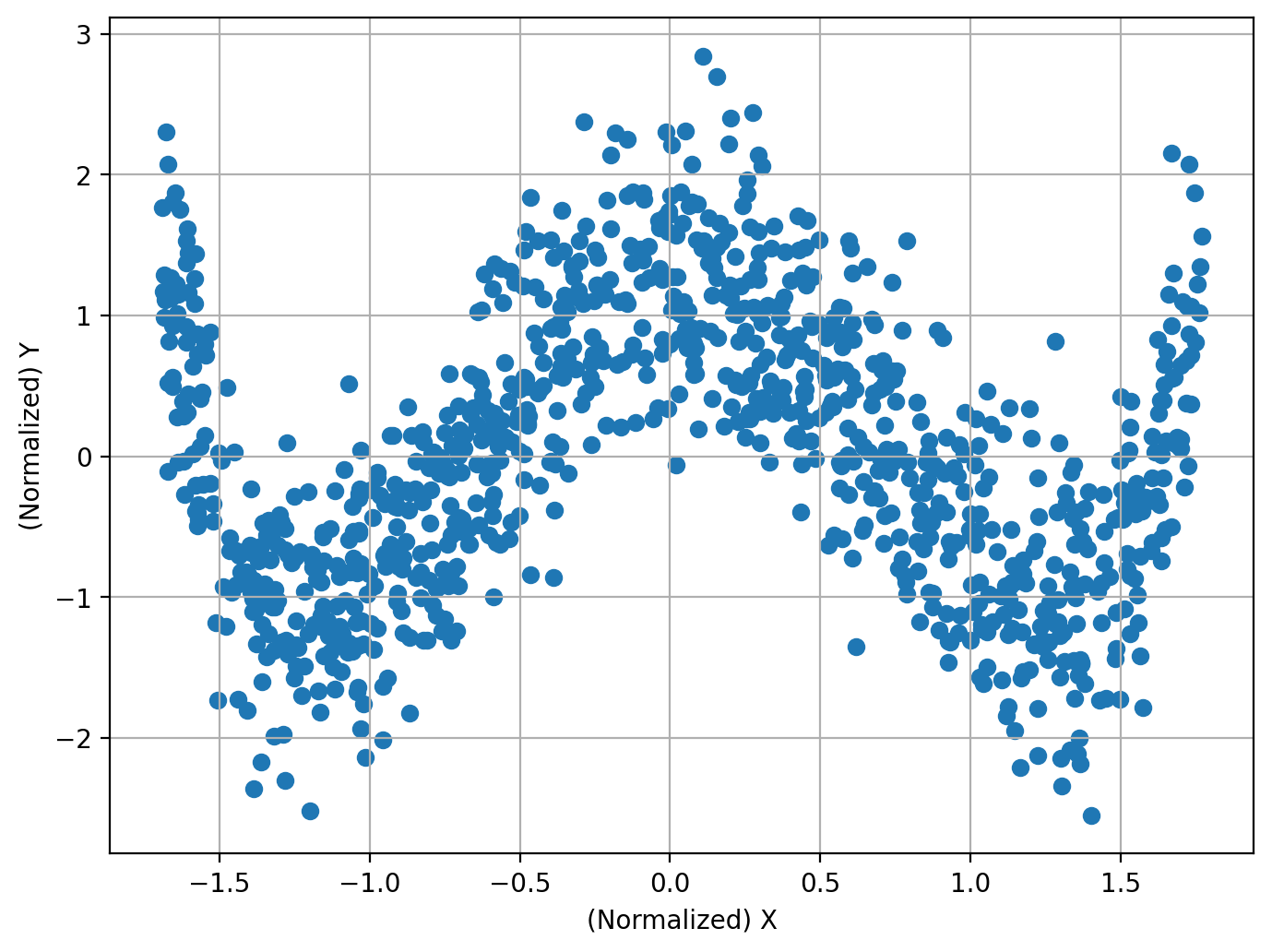
print(f'相関係数: {round(np.corrcoef(X_normalized.flatten(),Y_normalized.flatten())[0,1], 3)}')
相関係数: 0.004
H0Reject, testStat, thresh, pvalue = HSIC_test(X, Y, alpha = 0.05)
print(f'帰無仮説は棄却されるか?: {H0Reject}')
print(f'P値: {pvalue}')
帰無仮説は棄却されるか?: True
P値: 2.967448700752687e-77
反比例#
N = 1000
X = np.r_[-np.logspace(-3,-1,int(N/2)),np.logspace(-3,-1,int(N/2))].reshape(-1,1)
Y = 1/X + 10*np.random.normal(size=[N,1])
X_normalized = st.zscore(X)
Y_normalized = st.zscore(Y)
plt.figure(figsize=[8,6], dpi=200)
plt.scatter(X_normalized, Y_normalized)
plt.xlabel('(Normalized) X')
plt.ylabel('(Normalized) Y')
plt.grid()
plt.show()

print(f'相関係数: {round(np.corrcoef(X_normalized.flatten(),Y_normalized.flatten())[0,1], 3)}')
相関係数: 0.091
H0Reject, testStat, thresh, pvalue = HSIC_test(X, Y, alpha = 0.05)
print(f'帰無仮説は棄却されるか?: {H0Reject}')
print(f'P値: {pvalue}')
帰無仮説は棄却されるか?: True
P値: 0.0
三角関数#
N = 1000
X = np.random.uniform(-2,2,size=[N,1])
Y = np.sin(np.pi*X) + np.random.normal(size=[N,1])
X_normalized = st.zscore(X)
Y_normalized = st.zscore(Y)
plt.figure(figsize=[8,6], dpi=200)
plt.scatter(X_normalized, Y_normalized)
plt.xlabel('(Normalized) X')
plt.ylabel('(Normalized) Y')
plt.grid()
plt.show()
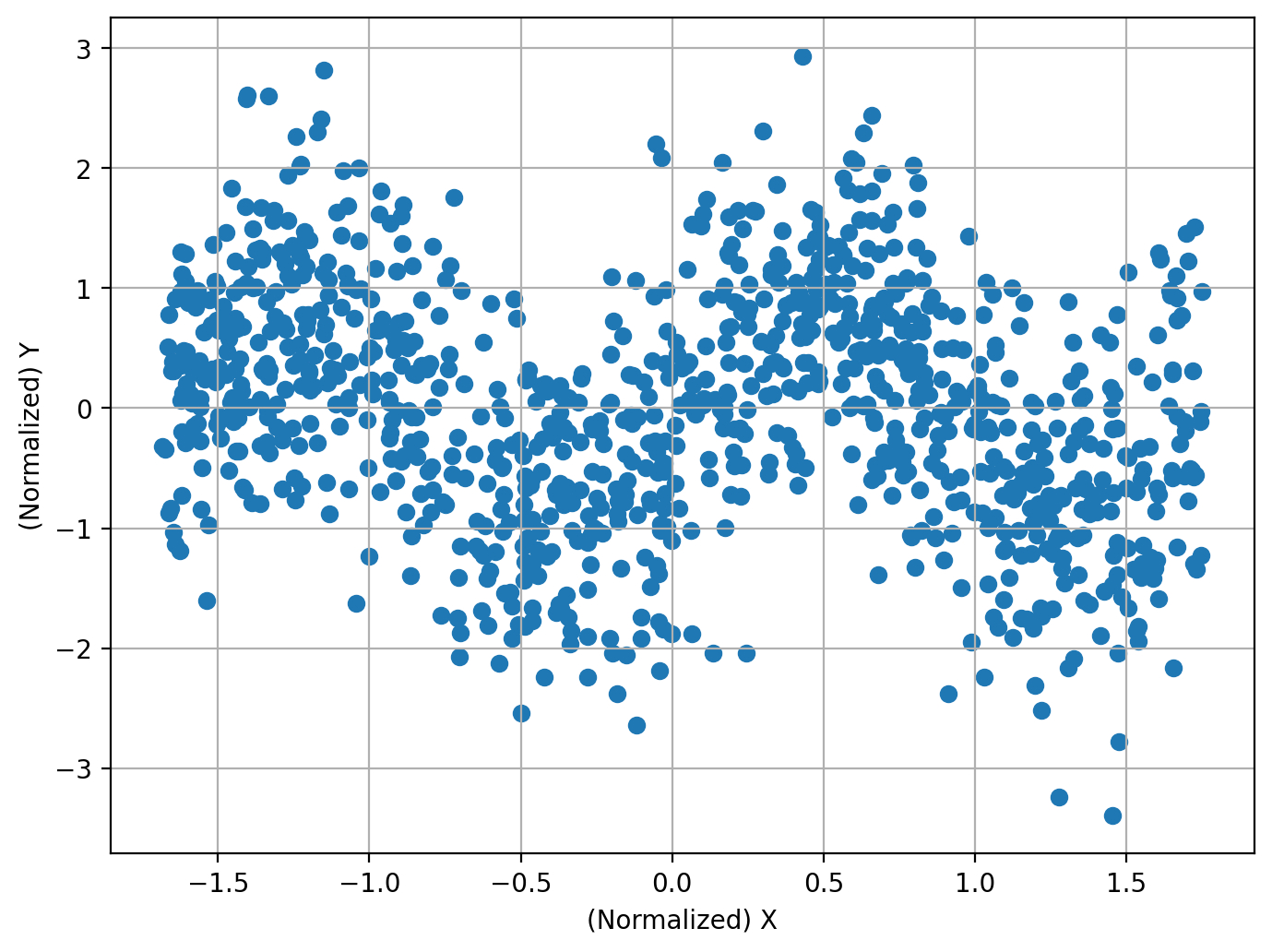
print(f'相関係数: {round(np.corrcoef(X_normalized.flatten(),Y_normalized.flatten())[0,1], 3)}')
相関係数: -0.22
H0Reject, testStat, thresh, pvalue = HSIC_test(X, Y, alpha = 0.05)
print(f'帰無仮説は棄却されるか?: {H0Reject}')
print(f'P値: {pvalue}')
帰無仮説は棄却されるか?: True
P値: 1.2294125276332267e-18
円#
N = 1000
theta = np.linspace(0,2*np.pi,N).reshape(-1,1)
X = 5*np.cos(theta) + np.random.normal(size=[N,1])
Y = 5*np.sin(theta) + np.random.normal(size=[N,1])
X_normalized = st.zscore(X)
Y_normalized = st.zscore(Y)
plt.figure(figsize=[8,6], dpi=200)
plt.scatter(X_normalized, Y_normalized)
plt.xlabel('(Normalized) X')
plt.ylabel('(Normalized) Y')
plt.grid()
plt.show()

print(f'相関係数: {round(np.corrcoef(X_normalized.flatten(),Y_normalized.flatten())[0,1], 3)}')
相関係数: -0.003
H0Reject, testStat, thresh, pvalue = HSIC_test(X, Y, alpha = 0.05)
print(f'帰無仮説は棄却されるか?: {H0Reject}')
print(f'P値: {pvalue}')
帰無仮説は棄却されるか?: True
P値: 5.260714610535346e-39
一次関数#
相関係数でも抽出可能なシンプルな一次関数に対しても、HSICによる独立性検定は問題なく利用できます。
N = 1000
X = np.random.uniform(-2,2,size=[N,1])
Y = X + np.random.normal(size=[N,1])
X_normalized = st.zscore(X)
Y_normalized = st.zscore(Y)
plt.figure(figsize=[8,6], dpi=200)
plt.scatter(X_normalized, Y_normalized)
plt.xlabel('(Normalized) X')
plt.ylabel('(Normalized) Y')
plt.grid()
plt.show()
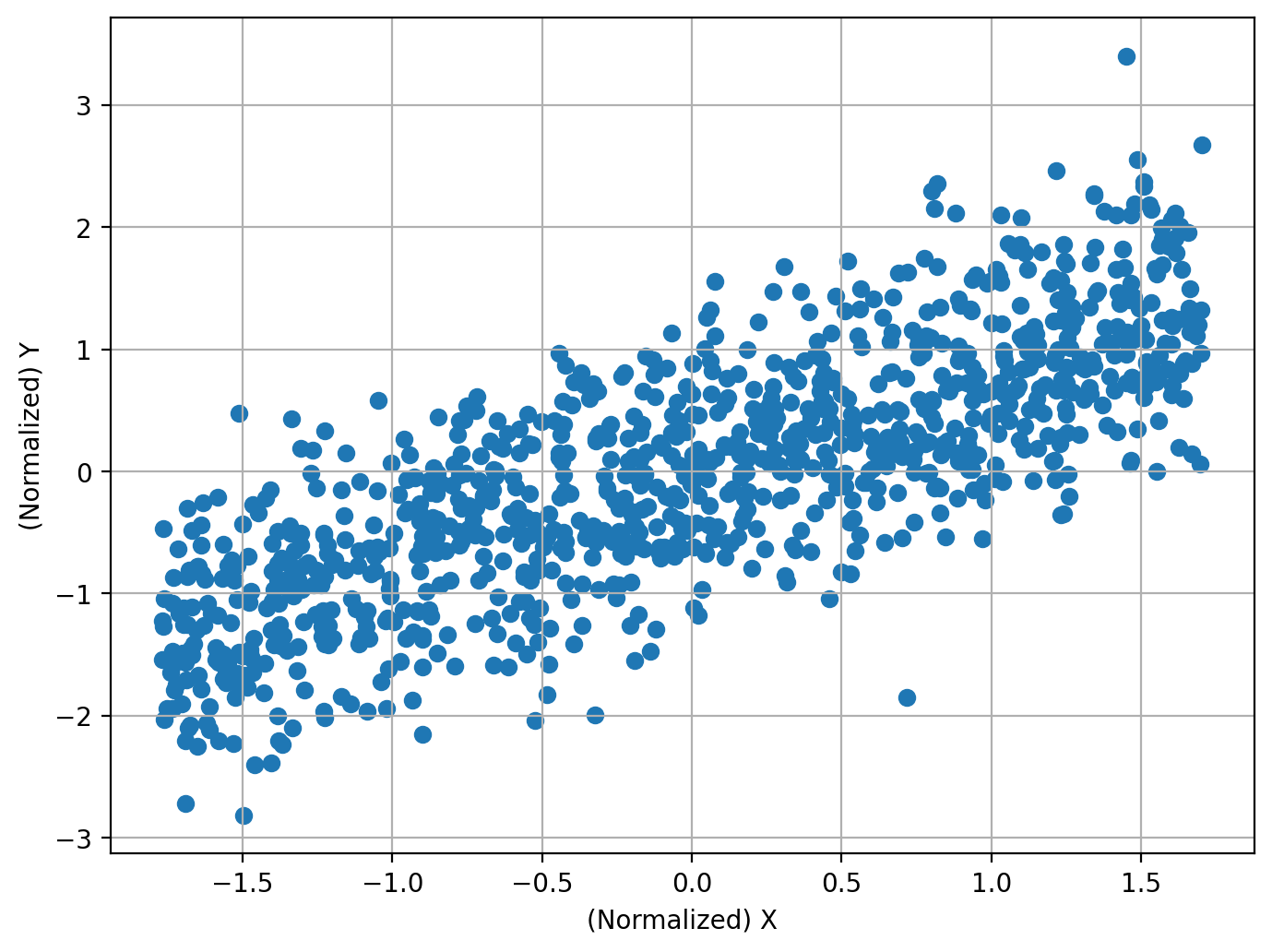
print(f'相関係数: {round(np.corrcoef(X_normalized.flatten(),Y_normalized.flatten())[0,1], 3)}')
相関係数: 0.79
H0Reject, testStat, thresh, pvalue = HSIC_test(X, Y, alpha = 0.05)
print(f'帰無仮説は棄却されるか?: {H0Reject}')
print(f'P値: {pvalue}')
帰無仮説は棄却されるか?: True
P値: 2.2158619133318178e-198
独立(依存関係が存在しない場合)#
2つの変数が完全に独立で依存関係が存在しない場合には、HSICによる独立性検定は帰無仮説を棄却しません。
すなわち、「2つの変数が独立ではないといえない」( \(\fallingdotseq\) 独立だ)と結論づけることができます。
N = 1000
X = np.random.normal(size=[N,1])
Y = np.random.normal(size=[N,1])
X_normalized = st.zscore(X)
Y_normalized = st.zscore(Y)
plt.figure(figsize=[8,6], dpi=200)
plt.scatter(X_normalized, Y_normalized)
plt.xlabel('(Normalized) X')
plt.ylabel('(Normalized) Y')
plt.grid()
plt.show()
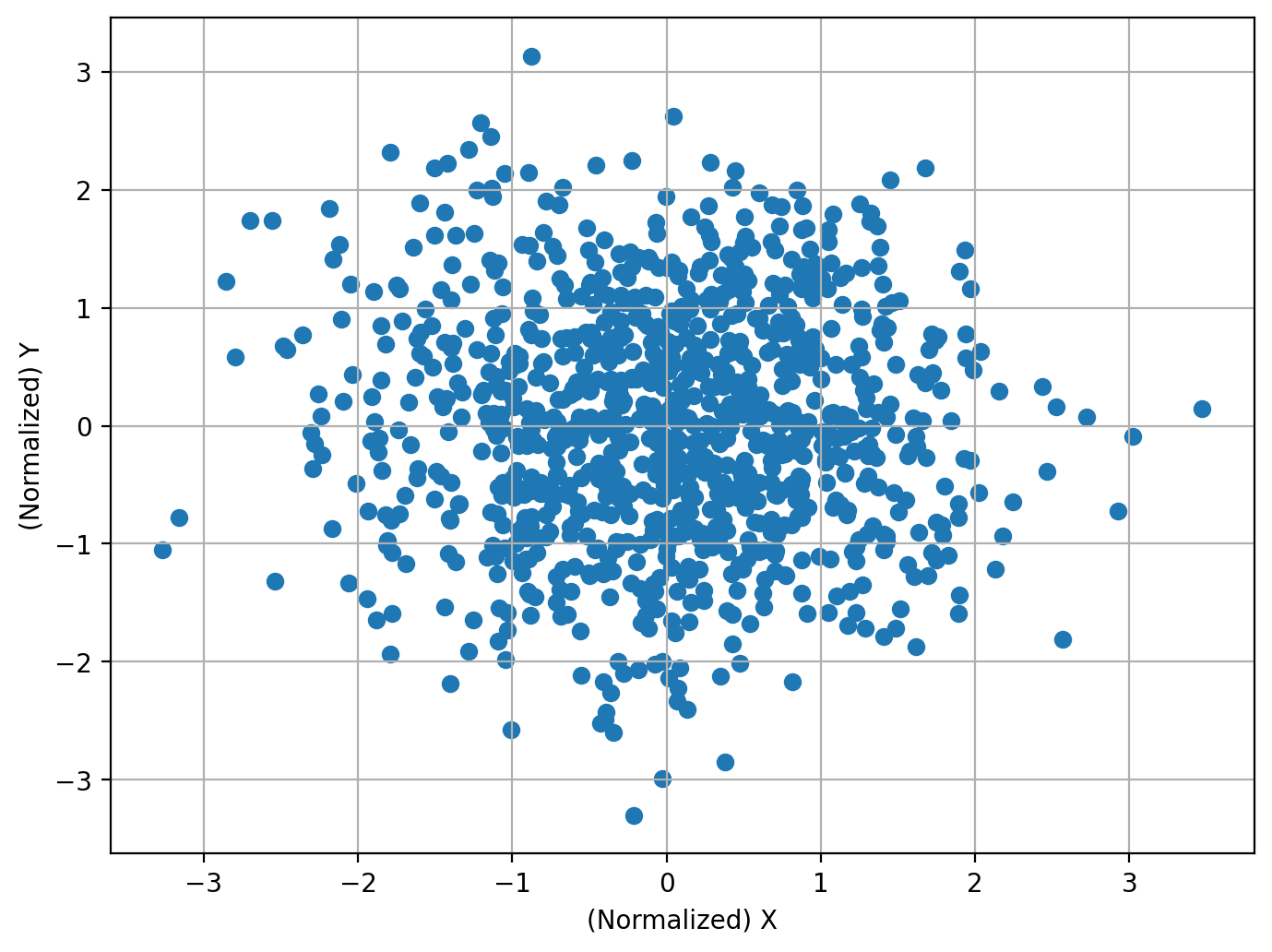
print(f'相関係数: {round(np.corrcoef(X_normalized.flatten(),Y_normalized.flatten())[0,1], 3)}')
相関係数: -0.023
H0Reject, testStat, thresh, pvalue = HSIC_test(X, Y, alpha = 0.05)
print(f'帰無仮説は棄却されるか?: {H0Reject}')
print(f'P値: {pvalue}')
帰無仮説は棄却されるか?: False
P値: 0.6506885639824664
小括#
いかがでしたでしょうか?
実際の現象に内在する変数間の関係性が純粋な線形ということは、きっとめったにないんだろうと思いますので、このHilbert-Schmidt独立性基準(HSIC)をデータ分析に取り入れることで解析の応用の幅が広がるのではないかと考えています。
本稿に興味を持っていただいた方はぜひカーネル法についても学んでみてください!
参考文献#
付録#
Hilbert空間(Hilbert Space)#
有限次元Euclid空間の一般化
特に断りがない場合は内積が定義された完備な無限次元空間
難しいので深入りしないの精神
(実)正定値カーネル#
\(k:\mathcal{X}\times\mathcal{X}\to\mathbb{R}\)が\(\mathcal{X}\)上の(実)正定値カーネルであるとは、次の2つを満たすことをいう。
対称性
正定値性
任意の自然数\(n\)と\(x_1,\cdots,x_n\in\mathcal{X}\)に対して
が(半)正定値、すなわち任意の実数\(c_1,\cdots,c_n\)に対して
また、\(\mathcal{V}\)を内積\(\langle\cdot,\cdot\rangle\)をもつベクトル空間とし、写像\(\Phi:\mathcal{X}\to\mathcal{V}\)が与えられているとすると
で定義されるカーネルは正定値カーネルとなる。
従って、特徴ベクトルの内積は正定値カーネルとなる。
再生核Hilbert空間(RKHS)#
集合\(\mathcal{X}\)上の関数からなるHilbert空間であって、任意の\(x\in\mathcal{X}\)に対して\(\phi_x(\cdot)=k(\cdot,x)\in\mathcal{H}\)が存在し、以下の関係を満たすもの。
このとき、\(\phi_x(\cdot)=k(\cdot,x)\)は再生核であり、再生核が存在すれば対応するRKHSは一意に存在する。
再生核Hilbert空間\(\mathcal{H}\)の再生核\(k\)は正定値カーネルとなる。
対称性
正定値性
\(\Phi(x):=\phi_x=k(\cdot,x)\)と再生性から
Moore-Aronszajnの定理#
\(k(x,y)\)を集合\(\mathcal{X}\)上の正定値カーネルとすると、\(\mathcal{X}\)上の関数からなるHilbert空間\(\mathcal{H}_k\)で次の3つを満たすものが一意に存在する。
\(k(\cdot,x)\in\mathcal{H}_k\) (\(x\in\mathcal{X}\)は任意に固定)
有限和\(f=\sum_{i=1}^nc_ik(\cdot,x_i)\)の元は\(\mathcal{H}_k\)の中で調密
再生性\(f(x)=\langle f,k(\cdot,x)\rangle_{\mathcal{H}_k}\) \((^{\forall}f\in\mathcal{H}_k,x\in\mathcal{X})\)
従ってカーネルトリック\(k(x,y)=\langle\Phi(x),\Phi(y)\rangle_{\mathcal{H}_k}\)が成り立つためには、正定値カーネル\(k\)を用意して
となる特徴写像\(\Phi\)を考えれば十分である。
独立性#
\(m\)次元確率変数\(X\)と\(n\)次元確率変数\(Y\)が独立であるとは、任意の可測集合\(\mathcal{X}\)と\(\mathcal{Y}\)に対し、
が成り立つことで、これを\(X\perp Y\)と表記する。
\(X\perp Y\)ならば\(E[f(X)g(Y)]=E[f(X)]E[g(Y)]\)である。
また\((X,Y)\)の分布が確率密度関数\(p_{XY}(x,y)\)をもつとき、それぞれの周辺分布の密度関数を\(p_X(x)\)と\(p_Y(y)\)とすると\(X\perp Y\Leftrightarrow p_{XY}(x,y)=p_X(x)p_Y(y)\)である。
独立性評価尺度のアイディア#
以下が成り立つ。
独立性(依存性)尺度として次を使えないか?
しかし、すべての可測関数を評価することは不可能。
また有限サンプルでどうやって推定するのか?
→再生核Hilbert空間で考えよう!
カーネル平均#
\(X\)を可測空間\((\mathcal{X},\mathcal{B})\)に値を取る確率変数とし、\(k\)を\(\mathcal{X}\)上の可測な正定値カーネル、\(\mathcal{H}_k\)を\(k\)の定める一意なRKHSとする。
(\(\mathcal{B}\)はボレル集合族であるが闇が深そうなので深入りしない)
このとき\(X\)の(\(\mathcal{H}_k\)における)カーネル平均は次のように定義される。
厳密には\(E[\|\Phi(X)\|]=E[\|k(\cdot,X)\|]<\infty\)のときカーネル平均が存在(Bochner積分)。
カーネル平均\(m_X\)もRKHSの元となる。
従って\(^{\forall}f\in\mathcal{H}_k\)に対して再生性が成り立つとともに、平均操作と内積は交換可能となる。
特性的な正定値カーネル#
可測空間\((\mathcal{X},\mathcal{B})\)上の可測かつ有界な正定値カーネル\(k\)が特性的であるとは
特性的なカーネルによって、カーネル平均\(m_X(=m_P)\)は分布\(P\)を一意に定める。
特性的なカーネルを用いることで分布\(P\)に関する推論問題をベクトル\(m_X(=m_P)\)に関する推論問題に置き換えることができる。
カーネル平均の推定#
i.i.d.な標本\(X_1,\cdots,X_n\)に対してカーネル平均の推定は
であり、この推定量\(\hat{m}_X^{(n)}\)には一致性がある。
共分散作用素#
\((X,Y)\)を\(\mathcal{X}\times\mathcal{Y}\)上の確率変数とし、\((\mathcal{H}_X,k_X)\)を\(\mathcal{X}\)上のRKHS、\((\mathcal{H}_Y,k_Y)\)を\(\mathcal{Y}\)上のRKHSとする。
このとき共分散作用素は次のように定義される。
共分散作用素はEuclid空間上の通常の確率ベクトル\(X\)と\(Y\)の共分散行列\(V_{YX}=E[YX^{\top}]\)の自然な拡張とみなせる。
\(^{\forall}f\in\mathcal{H}_X\)に対して\(C_{YX}f\)はRKHSの元となる。
従って\(^{\forall}f\in\mathcal{H}_X, {\:}^{\forall}g\in\mathcal{H}_Y\)に対して再生性を満たす。
共分散作用素は\(X\)と\(Y\)との関係を表現しているといえる。
また共分散作用素は次のように中心化することができる。
共分散作用素の推定#
i.i.d.な標本\((X_1,Y_1),\cdots,(X_n,Y_n)\sim P\)に対して共分散作用素の推定は
であり、この推定量\(\hat{C}_{YX}\)にも一致性がある。
また中心化した共分散作用素は次のように推定することができる。
Hilbert-Schmidtノルム#
Hilbert空間の間の作用素\(T:\mathcal{H}_X\to \mathcal{H}_Y\)がHilbert-Schmidtであるとは、\(\mathcal{H}_X\)と\(\mathcal{H}_Y\)の任意の正規直交基底\(\{f_i\}_i\)と\(\{g_j\}_j\)に対して
であることをいう。
このとき左辺の値は正規直交基底の取り方によらず
はHilbert-Schmidt作用素全体のなすベクトル空間にノルムを定める。
Hilbert-Schmidt独立性基準(HSIC)#
\((X,Y)\)を\(\mathcal{X}\times\mathcal{Y}\)上の確率変数とし、\((\mathcal{H}_X,k_X)\)を\(\mathcal{X}\)上のRKHS、\((\mathcal{H}_Y,k_Y)\)を\(\mathcal{Y}\)上のRKHSとする。
このときHilbert-Schmidt独立性基準を次のように定める。
またその推定は次のようになる。
積カーネル\(k_Xk_Y\)が\(\mathcal{X}\times\mathcal{Y}\)において特性的であればHSICと独立性は次の関係を満たす。
HSICはすべての任意の正規直交基底\(\{f_i\}_i\)と\(\{g_j\}_j\)の組みに関する共分散の二乗和である。
従って、HSICはすべての基底関数の組みに関して共分散を評価する指標といえ、\(\mathrm{HSIC}(X,Y)=0\)ならばすべての基底関数の組みに関して共分散が0で\(X\)と\(Y\)は独立である。
またHSICは積分表示をもち推定量を容易に求めることができる。
\((X',Y')\)を\((X,Y)\)の独立なコピーとする。
ここで、\(K_X\)と\(K_y\)はグラム行列で\(\tilde{K}_X\)と\(\tilde{K}_y\)は中心化されたグラム行列である。

