SymPyの使い方#
SymPyとは?#
SymPyはPythonの代数計算ライブラリです。
拡張しやすいように保ちコードのシンプルに保ちつつ、MathematicaやMapleのようなシステムの代替となることを目指しています。
SymPyはすべてPythonで書かれていて外部ライブラリを必要としないことも特徴のひとつです。
「習うより慣れろ」の精神で、徒然なるままに用法を書き下していきます。
SymPyライブラリの読み込み#
SymPyは簡単に使えます。
もし環境に入っていない場合は適当にpipとかしてください。
import sympy
sympy.init_printing(use_unicode=False, wrap_line=True)
四則演算#
加算#
3+2
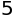
減算#
3-2
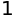
乗算#
3*2
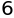
除算#
3/2
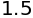
分数#
を分数表記。
sympy.Rational(3,2)
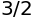
分母#
の分母。
sympy.denom(sympy.Rational(3,2))
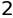
分子#
の分子。
sympy.numer(sympy.Rational(3,2))
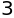
冪乗階乗#
冪乗#
3**2
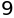
階乗#
sympy.factorial(50)
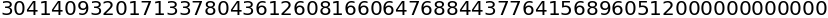
二重階乗#
二重階乗とは自然数\(n\)に対し一つ飛ばしに積を取る階乗のこと。
階乗の二回反復合成\((n!)!\)とは異なることに注意。
sympy.factorial2(50)
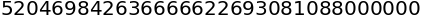
平方根#
sympy.sqrt(50)
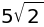
特殊定数#
円周率#
sympy.pi
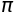
ネイピア数#
sympy.E
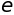
無限大#
sympy.oo
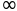
複素数#
虚数単位#
sympy.I
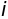
複素共役#
sympy.conjugate(2+3*sympy.I)
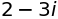
実部#
sympy.re(2+sympy.I*3)
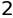
虚部#
sympy.im(2+sympy.I*3)
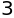
絶対値#
sympy.Abs(2+sympy.I*3)
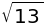
偏角#
sympy.arg(2+sympy.I*3)
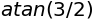
変数#
変数宣言#
x = sympy.Symbol('x')
y = sympy.Symbol('y')
z = sympy.Symbol('z')
a = sympy.Symbol('a')
b = sympy.Symbol('b')
c = sympy.Symbol('c')
算術演算#
x + y + x - y
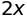
(x + y)**2
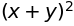
代数操作#
素因数分解#
sympy.factorint(sympy.factorial(10))
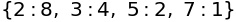
因数分解#
sympy.factor(x**2-4*x+3)
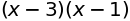
整数係数上既約の因数分解。
sympy.factor((1 + x - x**2)*(1 - x - x**2))
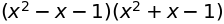
円分多項式上(mod 5で)既約の因数分解。
sympy.factor((1 + x - x**2)*(1 - x - x**2), modulus=5)
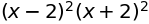
簡単化#
sympy.simplify((x + x*y)/x)
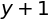
sympy.trigsimp(sympy.sin(x)/sympy.cos(x))

sympy.trigsimp((sympy.sin(a))**2+(sympy.cos(a))**2)
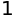
sympy.trigsimp((sympy.sinh(a))**2+(sympy.cosh(a))**2)
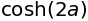
部分分数分解#
sympy.apart(1/(x**2-4*x+3))
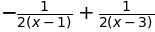
sympy.apart(1/(x**6-1))
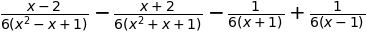
展開#
sympy.expand((x+y)**6)
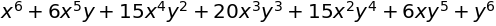
sympy.expand(sympy.tan(a+b), trig=True)
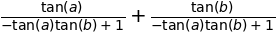
通分#
sympy.simplify((2*x-2)/((x-1)**2*(x-2)))
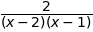
sympy.simplify(1/(x-1)**2+1/((x-1)*(x-2)))
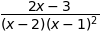
通分展開#
sympy.cancel((2*x-2)/((x-1)**2*(x-2)))
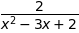
sympy.cancel(1/(x-1)**2+1/((x-1)*(x-2)))
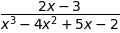
係数#
について\(x^3\)の係数。
sympy.expand((x+y)**6).coeff(x, 3)
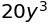
代入#
(a*x**2+b*x+c).subs(x, 3)
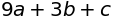
sympy.expand((a*x**2+b*x+c).subs(x, (-b + sympy.sqrt(-4*a*c + b**2))/(2*a)))

総和#
sympy.summation(x, (x, 1, 10))
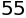
sympy.factor(sympy.summation(x, (x, 1, a)))
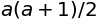
sympy.factor(sympy.summation(x**3, (x, 1, a)))
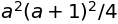
総乗#
sympy.product(x, (x, 1, 10))
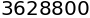
命題論理#
真偽判定#
0==sympy.sqrt(2)-2**(sympy.Rational(1,2))
True
0==sympy.sqrt(2)-2**(sympy.Rational(1,3))
False
sympy.factorial(10)==sympy.product(x, (x, 1, 10))
True
sympy.factorial(50)==sympy.factorial2(50)*sympy.factorial2(49)
True
ただし数式を適当に処理しないとうまく判定しない場合も多いので注意。
こちらは失敗している例。
x**2-2*x+1==(x-1)**2
False
例えば明示的に展開操作をすることで正しく真偽判定ができる。
x**2-2*x+1==sympy.expand((x-1)**2)
True
論理式#
sympy.satisfiable(x & y)
{x: True, y: True}
sympy.satisfiable(x & ~x)
False
解析操作#
関数定義#
def f(x):
return sympy.log(1+x)/x
f(x)
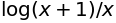
極限#
sympy.limit(sympy.sin(x)/x, x, 0)
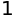
sympy.limit(x, x, sympy.oo)
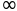
sympy.limit(1/x, x, sympy.oo)

sympy.limit(x**x, x, 0)
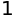
微分#
sympy.diff((x+y)**3, x)
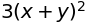
sympy.diff((x+y)**3, y, 2)
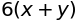
sympy.diff(sympy.tan(x), x)
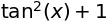
sympy.limit((sympy.tan(x+y) - sympy.tan(x))/y, y, 0)
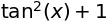
sympy.diff(f(x), x, 1)

級数展開#
sympy.series(sympy.cos(x), x)
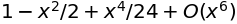
sympy.series(1/sympy.cos(x), x)
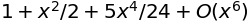
先ほどの\(f(x)\)を\(x=0\)の周りで7次未満の項まで展開してみる。
sympy.series(f(x), x, 0, 7)
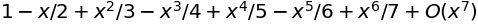
積分#
sympy.integrate(x+y, x)
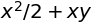
sympy.integrate(2*x + sympy.sinh(x), x)
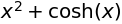
sympy.integrate((x+y)**3, (x, 0, 6))
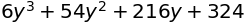
sympy.integrate(sympy.exp(-x**2), (x, -sympy.oo, sympy.oo))
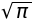
(ただし\(\mathrm{erf}\)は誤差関数。)
sympy.integrate(sympy.exp(-x**2)*sympy.erf(x), x)
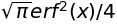
(ただし\(\mathrm{Li}_s\)は多重対数関数。)
sympy.integrate(f(x), x)
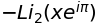
代数方程式#
求解#
を\(x\)について解く。
sympy.solve(x**4 - 1, x)
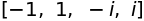
を連立させて\((x,y)\)について解く。
sympy.solve([x + 5*y - 2, -3*x + 6*y - 15], [x, y])
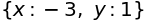
を\(x\)について解く。
sympy.solve(sympy.exp(x) + 1, x)
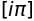
を\(x\)について解く。
sympy.solve (a*x**2+b*x+c, x)
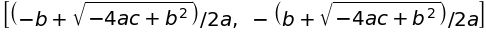
等式#
を\(x\)について解く。
ここでsympy.Eqは第1引数=第2引数の方程式を返す。
equation = sympy.Eq(x+1, (x+1)/(x**2+x-2))
sympy.solve(equation, x)
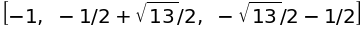
の右辺。
equation.rhs
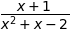
の左辺。
equation.lhs
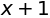
線形代数#
行列#
sympy.Matrix([[1,x], [y,1]])
sympy.Matrix([[1,x], [y,1]])**2
基本操作#
の(行)階段形。
sympy.Matrix([[1,0,1,3], [2,3,4,7], [-1,-3,-3,-4]]).rref()
零空間#
sympy.Matrix([[1,2,3,0,0], [4,10,0,0,1]]).nullspace()
列空間#
の列空間。
sympy.Matrix([[1,1,2], [2,1,3], [3,1,4]]).columnspace()
特性方程式#
の特性方程式。
sympy.factor(sympy.Matrix([[3,-2,4,-2], [5,3,-3,-2], [5,-2,2,-2], [5,-2,-3,3]]).charpoly())
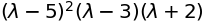
固有値固有ベクトル#
の固有値。
sympy.Matrix([[3,-2,4,-2], [5,3,-3,-2], [5,-2,2,-2], [5,-2,-3,3]]).eigenvects()
対角行列#
の対角化。
P, D = sympy.Matrix([[3,-2,4,-2], [5,3,-3,-2], [5,-2,2,-2], [5,-2,-3,3]]).diagonalize()
P, D
P * D * P**-1
微分方程式#
未知関数の定義#
f = sympy.symbols('f', cls=sympy.Function)
f(x)
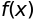
微分方程式の求解#
を満たす関数\(f(x)\)を求める。
sympy.dsolve(f(x).diff(x, x) + f(x), f(x))
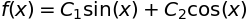
を満たす関数\(f(x)\)を求める。
sympy.dsolve(x*f(x).diff(x) + f(x) - f(x)**2)
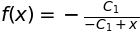
を満たす関数\(f(x)\)を求める。
この際にベルヌーイ型微分方程式であることをヒントとして与えることができる。
sympy.dsolve(x*f(x).diff(x) + f(x) - f(x)**2, f(x), hint='Bernoulli')
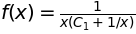
Tex形式出力#
コンパイル#
equation = sympy.Eq(a*x**2+b*x+c, 0)
solution = sympy.solve(equation, x)
sympy.init_printing()
solution
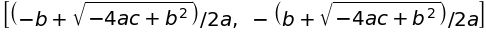
Tex出力#
print(sympy.latex(solution))
\left[ \frac{- b + \sqrt{- 4 a c + b^{2}}}{2 a}, \ - \frac{b + \sqrt{- 4 a c + b^{2}}}{2 a}\right]
小括#
PythonにおけるSymPyはStand Aloneであるにも関わらず、代数計算システムとして充実した機能を備えています。
まさにPythonの無限の可能性と、邪な開発意欲を感じさせるライブラリです。
【邪な例】
次の定積分を求めよ。
東京大学 平成31年度 第2次学力試験 数学(理科)第1問より抜粋
sympy.integrate((x**2+x/sympy.sqrt(1+x**2))*(1+x/(1+x**2)/sympy.sqrt(1+x**2)), (x, 0, 1))
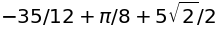
PythonにはSymPyのような楽しいライブラリがたくさん眠っているので、自ら発掘してみるのもとても楽しいかもしれません。
※(筆者の)必要に応じて今後も加筆する予定です。

