拡張カルマンフィルタとUnscentedカルマンフィルタ

拡張カルマンフィルタとUnscentedカルマンフィルタ#

カルマンフィルタでは、線形システムのためのカルマンフィルタについて解説しました。 ここでは、非線形システムのためのカルマンフィルタである拡張カルマンフィルタとUnscentedカルマンフィルタについて解説します。 また予測問題、フィルタリング問題、平滑化問題のうち、引き続きフィルタリング問題を取り扱います。 これ以降では、線形システムのためのカルマンフィルタをカルマンフィルタ、非線形システムのためのカルマンフィルタを非線形カルマンフィルタと呼び区別します。

非線形カルマンフィルタの概要#

カルマンフィルタについて少し振り返りつつ、非線形カルマンフィルタの概要ついて説明します。
カルマンフィルタでは大きく以下の3つの仮定をおいていました。

  • 対象とするシステムが線形であること

  • 雑音がガウス分布に従うこと

  • 雑音が白色であること

これらの仮定によりシステムの状態 \(x_k\) の予測分布 \(p(x_k|Y_{k-1})\) とフィルタ分布 \(p(x_k|Y_{k})\) はガウス分布となり、 各時刻 \(k\) において、これらの分布の平均ベクトルと共分散行列をカルマンフィルタで解析的に求めることが可能となるのでした。 また状態推定値 \(\hat{x}_{k|k} \) は \(p(x_k|Y_k)\) の平均ベクトルであるため、\(p(x_k|Y_k)\) の平均ベクトルが解析的に求まるということは、状態推定値が厳密に求まることを意味していました。

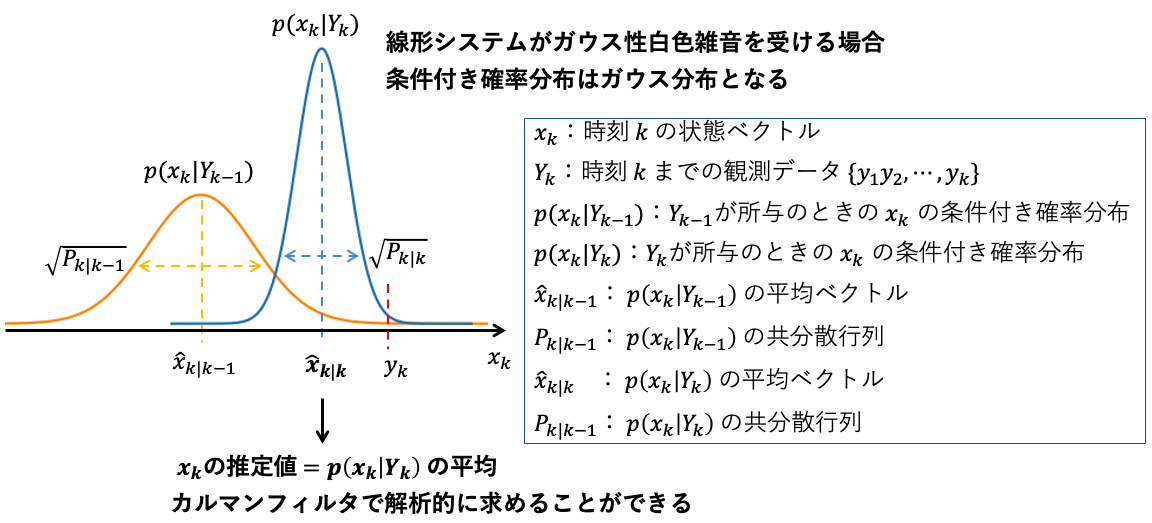
linear_kalman_process


それに対し非線形カルマンフィルタでは、システムの状態空間モデルに非線形関数が含まれるシステムを対象とします。

\[\begin{split} \begin{align*} x_{k+1} &= f_k(x_k, w_k) \qquad {状態方程式} \\ y_{k} &= h_k(x_k, v_k) \qquad {観測方程式} \end{align*} \end{split}\]

  • \( x_k \in \mathbb{R}^{n} : \) 状態ベクトル

  • \( y_k \in \mathbb{R}^{l} : \) 観測ベクトル

  • \( w_k \in \mathbb{R}^{m} : \) 白色性のシステム雑音

  • \( v_k \in \mathbb{R}^{p} : \) 白色性の観測雑音

  • \( f_k : \mathbb{R}^{n} \times \mathbb{R}^{m} \rightarrow \mathbb{R}^{n} \)

  • \( h_k : \mathbb{R}^{n} \times \mathbb{R}^{p} \rightarrow \mathbb{R}^{l} \)

上の非線形システムにおいて、\(k\) は時刻を表しており、\(k\) が添え字についた変数や関数はそれらが時刻と共に変化しうることを意味します。
\(f_k\) と \(h_k\) は一般の非線形関数になります。\(w_k\) と \(v_k\) はガウス分布とは限りません。 システムが線形であり雑音がガウス分布に従う場合との大きな違いは、システムの線形性と雑音のガウス性のいずれかが失われると、 \(x_k\) の条件付き確率分布 \(p(x_k|Y_{k-1})\) と \(p(x_k|Y_k)\) がガウス分布とはならないことです。

まずはこのことを具体例を通して確認しましょう。
簡単のため、時刻 \(k-1\) のフィルタ分布 \(p(x_{k-1}|Y_{k-1})\) がガウス分布であったとします。この状況で、時刻 \(k\) の予測分布 \(p(x_{k}|Y_{k-1})\) もまたガウス分布となるかを確認していきます。

\[\begin{split} \begin{align*} p(x_{k-1}|Y_{k-1}) &= \mathcal{N}(x_{k-1}; \hat{x}_{k-1|k-1}, \hat{P}_{k-1|k-1}) \\ &= \mathcal{N}(x_{k-1};~ 1,~ 2) \end{align*} \end{split}\]

上のガウス分布からサンプリングし、ヒストグラムを \(p(x_{k-1}|Y_{k-1})\) としてプロットしてみます。

Hide code cell source 
import numpy as np
import matplotlib.pyplot as plt
Hide code cell source 
mu = 1
cov = 2
n_samples = 2 * 10**5
x_hat_past = np.random.normal(mu, np.sqrt(cov), n_samples)

dx = 0.05
xl, xr = (mu - 4 * np.sqrt(cov), mu + 4 * np.sqrt(cov))
bins = np.arange(xl, xr, dx)
freq, bins = np.histogram(x_hat_past, bins=bins, density=True)

fig, ax = plt.subplots(1, 1)
ax.bar(
    bins[:-1],
    freq,
    align="edge",
    width=dx,
    color="steelblue",
    alpha=0.5,
    label="$p(x_{k-1}|Y_{k-1})$",
)
ax.vlines(mu, 0, 0.3, colors="violet", linestyles=":")
ax.vlines(mu - cov, 0, 0.3, colors="gold", linestyles=":")
ax.vlines(mu + cov, 0, 0.3, colors="gold", linestyles=":")
ax.set_xlim(xl, xr)
ax.legend()

plt.show()
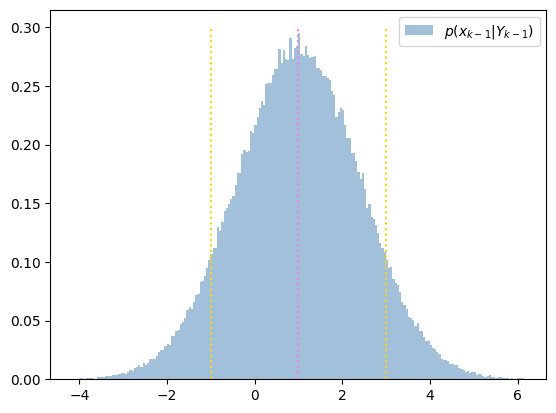
../_images/8ef8f994a43dbae3f5fd9b8124a6cfec80499080c810181b143345f717f26d97.png

平均と平均±標準偏差の位置に縦線をあわせてプロットしています。
フィルタ分布 \(p(x_{k-1}|Y_{k-1})\) からサンプリングした点を状態方程式により遷移させることで、時刻 \(k\) の予測分布 \(p(x_k|Y_{k-1})\) を求めてみます。 まずは状態方程式が線形であり雑音がガウス分布に従うと仮定します。なおここでは時刻 \(k-1\) から \(k\) への遷移を考えているため、状態方程式もそれに合わせた形で表記します。

\[\begin{split} \begin{align*} x_{k} &= x_{k-1} + w_{k-1} \\ w_{k-1} &\sim \mathcal{N}(0,~ 0.2) \end{align*} \end{split}\]
Hide code cell source 
cov_w = 0.2
x_hat_pred = x_hat_past + np.random.normal(0, np.sqrt(cov_w), n_samples)

dx = 0.05
xl, xr = (mu - 4 * np.sqrt(cov), mu + 4 * np.sqrt(cov))
bins = np.arange(xl, xr, dx)
freq, bins = np.histogram(x_hat_pred, bins=bins, density=True)

fig, ax = plt.subplots(1, 1)
ax.bar(
    bins[:-1],
    freq,
    align="edge",
    width=dx,
    color="steelblue",
    alpha=0.5,
    label="$p(x_{k}|Y_{k-1})$",
)
ax.set_xlim(xl, xr)

# カルマンフィルタの予測ステップの式から予測分布の平均と分散を求める
# mu_pred = F * mu = 1 * mu
# cov_pred = F * cov * F.T + cov_w = 1 * cov * 1 + cov_w
mu_pred = mu
cov_pred = cov + cov_w

ax.vlines(mu_pred, 0, 0.3, colors="violet", linestyles=":")
ax.vlines(mu - cov_pred, 0, 0.3, colors="gold", linestyles=":")
ax.vlines(mu + cov_pred, 0, 0.3, colors="gold", linestyles=":")
ax.legend()

plt.show()
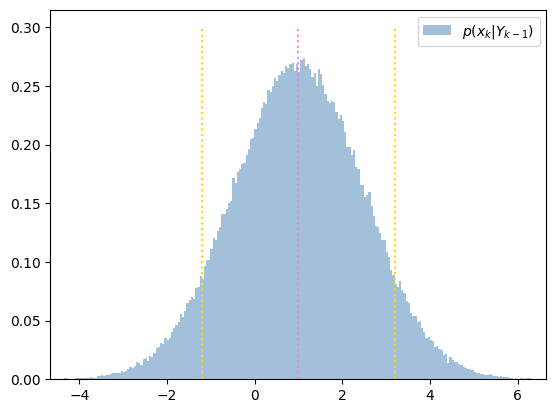
../_images/94b7d90dc782af5bb9340e9210e0562d4f25ca1bef67b7196743e7f34e03d092.png

ガウス分布の形が確認できます。 これは状態方程式の線形性と雑音のガウス性により、フィルタ分布の \(p(x_{k-1}|Y_{k-1})\) のガウス性が保たれ、予測分布 \(p(x_k|Y_{k-1})\) もまたガウス分布となったためです。 またこの場合、カルマンフィルタの予測ステップにより予測分布の平均と分散を求めることが可能です。 平均と分散を求め、平均と平均±標準偏差の位置に縦線をあわせてプロットしています。

さて、次に状態方程式が非線形である場合の様子を確認してみます。雑音は引き続きガウス分布に従うとします。

\[\begin{split} \begin{align*} x_{k} &= 0.5 x_{k-1} + 0.5 \sin(x_{k-1}) + w_{k-1} \\ w_{k-1} &\sim \mathcal{N}(0,~ 0.2) \end{align*} \end{split}\]

原点近傍では線形性があり、少し離れた位置で非線形性を持つ関数です。

Hide code cell source 
x_ = np.arange(-6, 6, 0.01)
alpha = 0.5
x_next_ = alpha * x_ + (1 - alpha) * np.sin(x_)

fig, ax = plt.subplots(1, 1)
ax.grid(True)
ax.plot(x_, x_next_, color="steelblue", label="$x_k = 0.5 x_{k-1} + \sin(x_{k-1})$")
ax.set_xlabel("$x_{k-1}$")
ax.set_ylabel("$x_k$")
ax.legend()

plt.show()
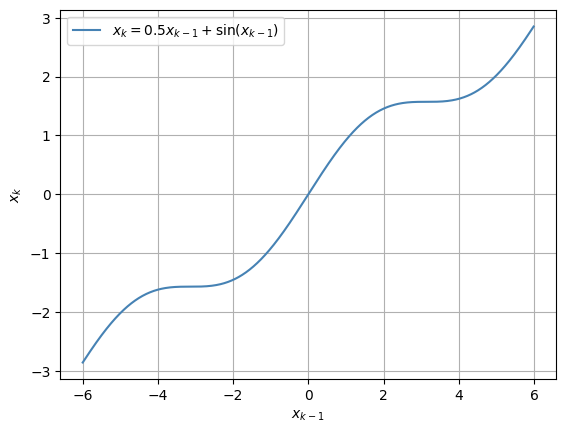
../_images/81a7c0a5ac28499da5f9efd3d1c525dfa4d935031e94fa763f1cbf323cdfd7bf.png

予測分布 \(p(x_k|Y_{k-1})\) を求めます。

Hide code cell source 
alpha = 0.5
x_pred = alpha * x_hat_past + (1 - alpha) * np.sin(x_hat_past)
x_pred += np.random.normal(0, np.sqrt(cov_w), n_samples)

dx = 0.05
xl, xr = (mu - 4 * np.sqrt(cov), mu + 4 * np.sqrt(cov))
bins = np.arange(xl, xr, dx)
freq, bins = np.histogram(x_pred, bins=bins, density=True)
fig, ax = plt.subplots(1, 1)
ax.bar(
    bins[:-1],
    freq,
    align="edge",
    width=dx,
    color="steelblue",
    alpha=0.5,
    label="$p(x_{k}|Y_{k-1})$",
)
ax.set_xlim(xl, xr)
ax.legend()

plt.show()
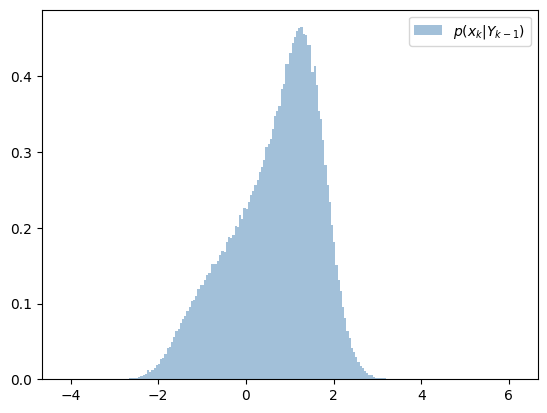
../_images/5c99bd3b95f5b959c7ab7616d5439c9e6cf67fffe873b07a05711cebe0d49dd8.png

フィルタ分布のガウス性が保たれず、予測分布はガウス分布とは異なる形状になっています。この例ではシステムの線形性のみが失われた場合の様子を確認しましたが、 システムの線形性もしくは雑音のガウス性のいずれかが失われると、予測分布 \(p(x_{k}|Y_{k-1})\) と フィルタ分布 \(p(x_{k}|Y_{k})\) は一般にガウス分布とはなりません。 そのためカルマンフィルタの場合のように、これらの分布の更新式を解析的に解くことが難しくなり、状態推定値であるフィルタ分布についての平均ベクトルを厳密に求めることが困難となります （条件付き確率分布の更新ついてはカルマンフィルタの導出を参照下さい）。 以上の背景のもと、拡張カルマンフィルタやUnscentedカルマンフィルタなどの非線形カルマンフィルタでは、何らかの近似により条件付き確率分布が計算されます。

拡張カルマンフィルタ#

それでは拡張カルマンフィルタについて説明します。非線形システムが以下の通り記述されるとします。

\[\begin{split} \begin{align*} x_{k+1} &= f_k(x_k) + w_k \\ y_k &= h_k(x_k) + v_k \\ \end{align*} \end{split}\]

\(f_k\) と \(h_k\) は非線形関数になります。これらが \( f_k(x_k, w_k) \) や \( h_k(x_k, v_k) \) の様により一般的な形をとる場合にも拡張カルマンフィルタは適用可能ですが[1]、簡単のためここでは雑音 \(w_k\) と \(v_k\) が \(f_k\) と \(h_k\) に加法的に加わるとします。 また \( w_k \) と \( v_k \) は平均が \(0\) で共分散行列がそれぞれ \(Q_k\) と \(R_k\) のガウス性の白色雑音であり、互いに独立とします。

\[\begin{split} \begin{align*} &w_k \sim \mathcal{N}(0, Q_{k}) \\ &v_k \sim \mathcal{N}(0, R_{k}) \\ % &\mathbb{E}[w_k] = 0\\ % &\mathbb{E}[v_k] = 0 \\ &\mathbb{E}[w_kw_s^T] = Q_k\delta_{ks} \\ &\mathbb{E}[v_kv_s^T] = R_k\delta_{ks} \\ &\mathbb{E}[v_kw_s^T] = 0, ~~k,s=0,1,\cdots \end{align*} \end{split}\]

雑音にガウス性を仮定するか否かは文献により異なるようです。ここではガウス性を仮定している文献[2] [3] に従っています。導出されるアルゴリズムに違いはありません。 なお雑音がガウス性であっても、前節の例で見たように \(x_k\) の条件付き確率分布は一般にガウス分布とはなりません。

この非線形システムにカルマンフィルタを適用することを考えます。アルゴリズムについてはカルマンフィルタのアルゴリズムを参照下さい。 カルマンフィルタでは線形システムの遷移行列 \(F_{k-1}\) 、駆動行列 \(G_{k-1}\) 、観測行列 \(H_k\) が必要となりますが、非線形システムの場合これらは存在しないため、そのままではカルマンフィルタを適用できません。そこで状態空間モデル内の非線形関数 \(f_k\) と \(h_k\) を必要に応じて線形近似し、線形化した結果を利用することを考えます。

まずは予測ステップから具体的に説明します。
今、時刻 \(k-1\) のフィルタ分布の平均ベクトル \( \hat{x}_{k-1|k-1} \) と共分散行列 \(P_{k-1|k-1}\) が得られているとします。予測ステップを適用するには、線形な状態方程式の遷移行列 \(F_{k-1}\) と駆動行列 \(G_{k-1}\) が必要となります。そこで \(f_{k-1}\) を直近の状態推定値である \( x_{k-1} = \hat{x}_{k-1|k-1} \) のまわりで1次のテーラー展開により線形近似します。

\[\begin{split} \begin{align*} x_{k} &= f_{k-1}(\hat{x}_{k-1|k-1}) + w_{k-1} \\ x_{k} &\simeq f_{k-1}(\hat{x}_{k-1|k-1}) + \left. \frac{\partial f_{k-1} }{\partial x_{k-1}} \right| _{\hat{x}_{k-1|k-1}} (x_{k-1}-\hat{x}_{k-1|k-1}) + w_{k-1} \\ \end{align*} \end{split}\]

\( \frac{\partial f_{k-1} }{\partial x_{k-1}} \) は多変数関数 \(f_{k-1} \)の各成分の偏導関数を並べた行列として定義され、ヤコビ行列と呼ばれます。 時刻が \(k\) の場合の定義を以下に示します。

\[\begin{split} \begin{align*} \frac{\partial f_k }{\partial x_k} = \begin{bmatrix} \frac{f_{k, 1}}{\partial x_{k, 1}} & \frac{\partial f_{k, 1}}{\partial x_{k, 2}} & \cdots & \frac{\partial f_{k, 1}}{\partial x_{k, n}} \\ \vdots & \vdots & \vdots & \vdots \\ \frac{f_{k, n}}{\partial x_{k, 1}} & \frac{\partial f_{k, n}}{\partial x_{k, 2}} & \cdots & \frac{\partial f_{k, n}}{\partial x_{k, n}} \\ \end{bmatrix} \end{align*} \end{split}\]
\[ \begin{align*} f_k = [f_{k, 1}~\cdots~f_{k,n}]^T, ~~x_k = [x_{k, 1}~\cdots~x_{k,n}]^T \end{align*} \]

\( \hat{F}_{k-1} = \left. \frac{\partial f_{k-1}}{\partial x_{k-1}} \right|_{\hat{x}_{k-1|k-1}} \) とおき、確率変数以外の項を外部入力 \({u}_{k-1}\) としてまとめます。

\[\begin{split} \begin{align*} x_{k} & \simeq f_{k-1}(\bar{x}_{k-1|k-1}) + \hat{F}_{k-1} (x_{k-1}-\hat{x}_{k-1|k-1}) + w_{k-1} \\ & = \hat{F}_{k-1} x_{k-1} + w_{k-1} + f_{k-1}(\hat{x}_{k-1|k-1}) - \hat{F}_{k-1} \hat{x}_{k-1|k-1} \\ & = \hat{F}_{k-1} x_{k-1} + w_{k-1} + u_{k-1} \\ \end{align*} \end{split}\]

線形近似により遷移行列 \( F_{k-1} \) に相当する行列として \(\hat{F}_{k-1} \) が得られました。また駆動行列 \(G_{k-1}\) は雑音 \(w_{k-1}\) にかかる行列であるため、 上の式において \(G_{k-1}\) に相当する行列は単位行列 \( I \) となります。 予測ステップではこれらを利用します。

続いて観測更新ステップです。
予測ステップにより時刻 \(k\) の予測分布の平均 \( \hat{x}_{k|k-1} \) と共分散行列 \(P_{k|k-1}\) が得られているとします。 カルマンフィルタの観測更新ステップを適用するには、線形な観測方程式に含まれる観測行列 \(H_k\) が必要になります。 そこで \(h_{k}\) を \( x_{k} = \hat{x}_{k|k-1} \) の近傍で1次のテーラー展開により線形近似します。

\[\begin{split} \begin{align*} y_{k} & = h_{k}(\hat{x}_{k|k-1}) + v_k \\ & \simeq h_{k}(\hat{x}_{k|k-1}) + \left. \frac{\partial h_{k} }{\partial x_{k}} \right|_{\hat{x}_{k|k-1}} (x_{k}-\hat{x}_{k|k-1}) + v_{k} \\ & = h_{k}(\hat{x}_{k|k-1}) + \hat{H}_{k} (x_{k}-\hat{x}_{k|k-1}) + v_{k} \\ & = \hat{H}_{k} x_{k} + v_{k} + h_{k}(\hat{x}_{k|k-1}) - \hat{H}_{k} \hat{x}_{k|k-1} \\ & = \hat{H}_{k} x_{k} + v_{k} + r_{k} \\ \end{align*} \end{split}\]

\( \hat{H}_{k} = \left. \frac{\partial h_{k}}{\partial x_{k}} \right|_{\hat{x}_{k|k-1}} \) とおき、確率変数以外の項を外部入力 \({r}_{k}\) としてまとめました。 こちらも外部入力を受ける場合の線形な観測方程式となっていることがわかります。外部入力の取り扱いについては後ほど補足します。 線形近似により \( H_{k} \) に相当する行列として \(\hat{H}_{k} \) が得られました。観測更新ステップではこれを利用します。

なお、\(f_k\) と \(h_k\) がより一般的な \(f_k(x_k, w_k)\) や \(h_k(x_k, v_k)\) の形をとる場合には、\(w_k\) と \(v_k\) の偏微分によるヤコビ行列も求めて整理する必要があります。 しかしその場合も外部入力を含む線形な状態方程式と観測方程式となる点は同じです。 ここまでの手順をまとめたものが拡張カルマンフィルタのアルゴリズムとなります。

拡張カルマンフィルタのアルゴリズム#

拡張カルマンフィルタのアルゴリズム

  • 初期値の設定

\[ \begin{align*} \hat{x}_{0|0} = \bar{x}_0, ~P_{0|0} = P_0 \end{align*} \]

\( k=1,2 \cdots \) に対して以下を繰り返します。

  • 予測ステップ

    \[\begin{split} \begin{align*} \hat{F}_{k-1} &= \left. \frac{\partial f_{k-1}}{\partial x_{k-1}} \right|_{\hat{x}_{k-1|k-1}} \\ \hat{x}_{k|k-1} &= f_{k-1} (\hat{x}_{k-1|k-1})　\\ P_{k|k-1} &= \hat{F}_{k-1} P_{k-1|k-1} \hat{F}_{k-1}^T + Q_{k-1} \end{align*} \end{split}\]

  • 観測更新ステップ

    \[\begin{split} \begin{align*} \hat{H}_{k} &= \left. \frac{\partial h_{k}}{\partial x_{k}} \right|_{\hat{x}_{k|k-1}} \\ K_k &= P_{k|k-1} \hat{H}_k^T (\hat{H}_k P_{k|k-1} \hat{H}_k^T + R_k)^{-1} \\ \hat{x}_{k|k} &= \hat{x}_{k|k-1} + K_k [y_k - h_k(\hat{x}_{k|k-1})] \\ P_{k|k} &= P_{k|k-1} - K_k \hat{H}_k P_{k|k-1} \end{align*} \end{split}\]

拡張カルマンフィルタのアルゴリズムは、カルマンフィルタのアルゴリズムと非常に似通ったものであることが分かります。 ここでは両者の相違点を中心に説明します。
拡張カルマンフィルタではヤコビ行列 \(\hat{F}_{k-1}\) と \(\hat{H}_{k}\) を求め、システムが線形な場合の \(F_{k-1}\) と \(H_k \) の代わりに利用します。 これは線形近似したシステムに対してカルマンフィルタを適用していることになります。
一方、\(\hat{x}_{k|k-1}\) と \(\hat{x}_{k|k}\) の計算では線形近似した関数ではなく、元の非線形な \(f_{k-1}\) と \(h_k\) が使われています。 状態方程式と観測方程式を利用した予測計算（雑音の項を除いて）が行われていた箇所では、非線形な式がそのまま利用されます。

状態方程式と観測方程式を線形近似した際に現れた外部入力 \(u_{k-1}\) と \(r_k\) についても補足します。 通常、状態方程式と観測方程式に外部入力が含まれるシステムにカルマンフィルタを適用する場合、アルゴリズム内の状態方程式と観測方程式にも外部入力を含める必要があります。 しかし上の通り拡張カルマンフィルタではこの部分に元の非線形関数を用いるため、線形近似の際に現れる外部入力について気にする必要はありません。

システムがカルマンフィルタでおく仮定を満たす場合、カルマンフィルタで求まる \(\hat{x}_{k|k-1}\) と \( P_{k|k-1}\) は、\(p(x_k|Y_{k-1})\) の平均ベクトルと共分散行列、 \(\hat{x}_{k|k}\) と \( {P}_{k|k}\) は、\(p(x_k|Y_k)\) の平均ベクトルと共分散行列の厳密値になっていました。 一方、非線形システムに拡張カルマンフィルタを適用し求まる \(\hat{x}_{k|k-1}, P_{k|k-1}, \hat{x}_{k|k}, {P}_{k|k}\) は、これらの分布の平均ベクトルと共分散行列の近似値となります。


Unscented変換#

拡張カルマンフィルタでは状態空間モデル内の非線形関数を必要に応じて線形近似し、カルマンフィルタのアルゴリズムに沿って \(x_k\) の平均ベクトルと共分散行列を近似計算していました。 これに対しUnscentedカルマンフィルタでは、非線形関数ではなく非線形関数により変換された確率分布をいくつかのサンプル点により近似計算します。 サンプル点はシグマポイントと呼ばれ、シグマポイントを非線形変換した点を用いて変換後の確率変数の平均ベクトルと共分散行列を近似計算します。 この方法はUnscented変換と呼ばれます。ここではUnscented変換について説明します。

非線形関数 \(h: \mathbb{R}^n \rightarrow \mathbb{R}^p\) により確率変数 \(x\) が \(y\) へ変換される状況で、変換後の確率変数 \(y\) の平均ベクトルと共分散行列を精度良く計算することを考えます。

\[ \begin{align*} y = h(x) \end{align*} \]

Unscented変換では、シグマポイントと呼ばれる \(2n+1\) 個の点を \(x\) の平均ベクトルを中心にまずサンプリングします。\(n\) は \(x\) の次元数です。
これにはいくつかのバリエーションがあり、以下は文献[3] [4]のものになります。

\[\begin{split} \begin{align*} x^{(0)} &= \bar{x} \\ x^{(i)} &= \bar{x} + \sqrt{n + \lambda} (\sqrt{P_x})_{i} ~, ~~~ i=1,\cdots n \\ x^{(n+i)} &= \bar{x} - \sqrt{n + \lambda} (\sqrt{P_x})_{i} ~, ~~~ i=1,\cdots n \\ \end{align*} \end{split}\]

\(\bar{x}\) と \(P_x\) は \(x\) の平均ベクトルと共分散行列、\((\sqrt{P_x})_i\) は \( \sqrt{P_x}\sqrt{P_x}^T = P_x \) を満たす行列の \(i\) 番目の列です。 この様な行列は平方根行列と呼ばれコレスキー分解や特異値分解を用いて求めることができます。

各シグマポイント \(x^{(i)}\) には、平均を計算するための重み \(W_m^{(i)}\) と共分散行列を計算するための \(W_c^{(i)}\) が割り当てられます。

\[\begin{split} \begin{align*} \lambda &= \alpha^2 (n + \kappa) - n \\ W_m^{(0)} &= \frac{\lambda}{n + \lambda} \\ W_c^{(0)} &= \frac{\lambda}{n + \lambda} + 1 - \alpha^2 + \beta\\ W_m^{(i)} &= \frac{1}{2(n + \lambda)}~, ~i=1,\cdots, 2n \\ W_c^{(i)} &= \frac{1}{2(n + \lambda)}~, ~i=1,\cdots, 2n \\ \end{align*} \end{split}\]

\(\alpha, \beta, \kappa\) は調整パラメータです。 \(\alpha\) はシグマポイントの平均からの広がりを調整するパラメータです。\(\alpha\) は小さな正の値に、\(\kappa\) は \(0\) もしくは \(3-n\) と設定されることが多いようです。 \(\beta\) については \(x\) がガウス分布に従う場合、 \(\beta=2\) が最適とされています。

シグマポイントを非線形関数 \(h\) で変換すると対応する \(y\) のサンプル点が得られます。

\[\begin{split} \begin{align*} y^{(i)} &= h(x^{(i)}) ~, ~~~ i=0,\cdots, 2n \\ \end{align*} \end{split}\]

サンプル点 \(y^{(i)}\) と重み \(W^{(i)}\) を用いて \(y\) の平均ベクトル \(\bar{y}\)と共分散行列 \(P_y\)、そして \(x\) と\(y\) の相互共分散行列 \(P_{xy}\) が近似計算されます。

\[\begin{split} \begin{align*} \mathbb{E}[y] &= \bar{y} \simeq \sum_{i=0}^{2n} W_m^{(i)} y^{(i)} \\ \mathbb{E}[(y-\bar{y})(y-\bar{y})^T] &= P_y \simeq \sum_{i=0}^{2n} W_c^{(i)} (y^{(i)}-\bar{y}) (y^{(i)}-\bar{y})^T \\ \mathbb{E}[(x-\bar{x})(y-\bar{y})^T] &= P_{xy} \simeq \sum_{i=0}^{2n} W_c^{(i)} (x^{(i)}-\bar{x}) (y^{(i)}-\bar{y})^T \\ \end{align*} \end{split}\]

上がUnscented変換による平均ベクトルと共分散行列の計算方法になります。それでは簡単な例に対して、Unscented変換により平均ベクトルと共分散行列を計算してみましょう。

変換前の確率変数 \(x\) が以下のガウス分布に従うとし、確率分布から適当な点数サンプリングします。

\[\begin{split} \begin{align*} &x \sim \mathcal{N}( \begin{bmatrix} 0 \\ 2 \end{bmatrix}, \begin{bmatrix} 0.4 & 0.04 \\ 0.04 & 0.4 \end{bmatrix} ) \end{align*} \end{split}\]

またサンプリングした点からシグマポイントと重みを計算します。

Hide code cell source 
import numpy as np
from numpy.random import multivariate_normal
import matplotlib.pyplot as plt
import matplotlib.patches as pat
Hide code cell source 
mu_x = np.array([0, 2])
cov_x = np.array([[0.4, 0.04], [0.04, 0.4]])
x = multivariate_normal(mu_x, cov_x, size=10**4)

nx = 2
kappa = 0
alpha = 1
beta = 2
lambda_ = alpha**2 * (nx + kappa) - nx

sigma_point_x = np.zeros((2 * nx + 1, nx))
L = np.linalg.cholesky(cov_x)  # L * L^T = cov_x
sigma_point_x[0] = mu_x
MU = np.tile(mu_x, (nx, 1))
sigma_point_x[1 : nx + 1] = MU + np.sqrt(nx + lambda_) * L.T
sigma_point_x[nx + 1 :] = MU - np.sqrt(nx + lambda_) * L.T
print("Sigma Points")
print(sigma_point_x)

Wm, Wc = np.zeros(2 * nx + 1), np.zeros(2 * nx + 1)
Wm[0] = lambda_ / (nx + lambda_)
Wc[0] = lambda_ / (nx + lambda_) + 1 - alpha**2 + beta
Wm[1:] = 1 / (2 * (nx + lambda_))
Wc[1:] = 1 / (2 * (nx + lambda_))

print("Weights (Mean)")
print(Wm)
print("Weights (Covariance)")
print(Wc)

Sigma Points
[[ 0.          2.        ]
 [ 0.89442719  2.08944272]
 [ 0.          2.88994382]
 [-0.89442719  1.91055728]
 [ 0.          1.11005618]]
Weights (Mean)
[0.   0.25 0.25 0.25 0.25]
Weights (Covariance)
[2.   0.25 0.25 0.25 0.25]

\(x\) の平均ベクトル、共分散行列、シグマポイントをプロットします。共分散行列については \(2\sigma\) を楕円として描きます。

Hide code cell source 
def get_covariance_ellipse(cov, n_std=2.0):
    # x^T * cov^(-1) * x = n_std^2 となる楕円のパラメータを計算
    vals, vecs = np.linalg.eigh(cov)
    width, height = 2 * n_std * np.sqrt(vals)
    angle = np.rad2deg(np.arctan2(vecs[1, 0], vecs[0, 0]))
    return width, height, angle


fig, ax = plt.subplots(1, 1, figsize=(6, 6))
ax.scatter(
    x[:, 0], x[:, 1], s=20, color="steelblue", edgecolor="none", alpha=0.2, label="x"
)
ax.scatter(
    sigma_point_x[:, 0],
    sigma_point_x[:, 1],
    s=50,
    color="gold",
    edgecolor="none",
    label="Sigma Point",
)
ax.scatter(mu_x[0], mu_x[1], s=25, color="red", edgecolor="none", label="Mean")

width, height, angle = get_covariance_ellipse(cov_x)
ell = pat.Ellipse(
    xy=mu_x,
    width=width,
    height=height,
    angle=angle,
    edgecolor="red",
    fc="none",
    lw=2,
    alpha=0.6,
    label="Covariance",
)
ax.add_patch(ell)
ax.set_xlabel("$x_1$")
ax.set_ylabel("$x_2$")
ax.legend()

plt.show()
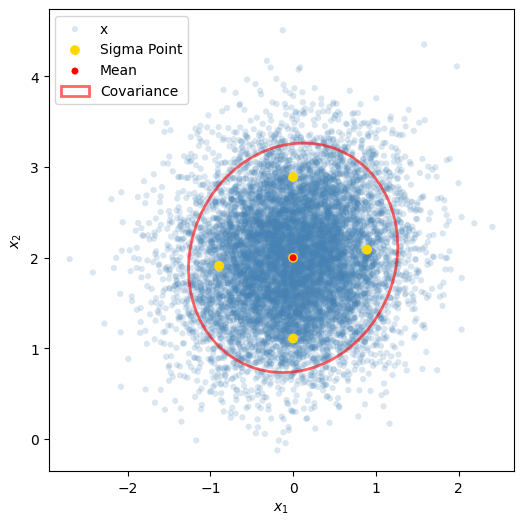
../_images/ce23ae7ae391da8d6fd68ba4985637f6d3290ca652bda4860aa29b8b2f686c8e.png

平均値を中心にシグマポイントが配置されていることが分かります。 非線形関数は以下の通りとします。

\[\begin{split} \begin{align*} y = h(x) = \begin{bmatrix} h_1(x_1) \\ h_2(x_2) \end{bmatrix} = \begin{bmatrix} 0.5x_1 + 0.5\sin(x_1) \\ 0.5x_2 + 0.5\sin(x_2) \end{bmatrix} \end{align*} \end{split}\]
Hide code cell source 
def nonlinear_transform(x):
    return 0.5 * x + 0.5 * np.sin(x)


x_ = np.arange(-4, 4, 0.01)
fig, ax = plt.subplots(1, 1)
ax.plot(x_, nonlinear_transform(x_), color="steelblue", label="y=0.5x+sin(x)")
ax.plot(x_, x_, ":", color="violet", label="y=x")
ax.legend()
ax.set_xlabel("x")
ax.grid(True)

plt.show()
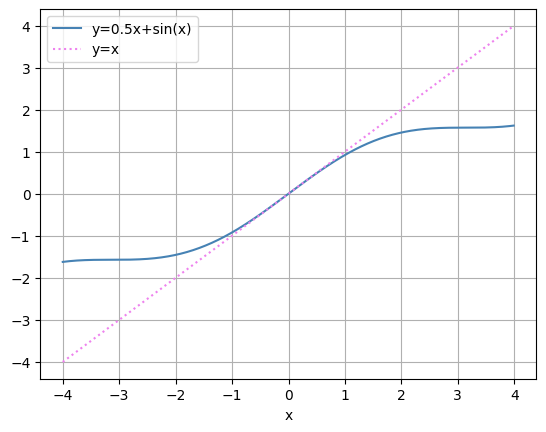
../_images/2a35545a758e8a938cbc7bd316405d9eb23dc28cfe3f947ae45b39013a1e39ba.png

サンプル点を非線形変換し、変換後の全てのサンプル点より標本平均と標本共分散行列を計算します。点数が十分多ければこれらは真の平均ベクトルと共分散行列に一致します。

Hide code cell source 
y = nonlinear_transform(x)
mu_y = np.mean(y, axis=0)
cov_y = np.cov(y, rowvar=False)
mu_y, cov_y

(array([-1.09541043e-03,  1.37197070e+00]),
 array([[0.33042479, 0.01257216],
        [0.01257216, 0.05254754]]))

シグマポイントも非線形変換し、Unscented変換の定義通りに平均ベクトルと共分散行列を計算します。

Hide code cell source 
sigma_point_y = nonlinear_transform(sigma_point_x)

ut_mu_y = np.sum(Wm[:, np.newaxis] * sigma_point_y, axis=0)
ut_cov_y = np.zeros_like(cov_y)
for i in range(sigma_point_y.shape[0]):
    dy = sigma_point_y[i] - ut_mu_y
    ut_cov_y += Wc[i] * np.outer(dy, dy)

ut_mu_y, ut_cov_y

(array([0.        , 1.36950627]),
 array([[0.35040079, 0.01093953],
        [0.01093953, 0.06191005]]))

Unscented変換との比較のため、非線形関数を線形近似し平均ベクトルと共分散行列を計算することにします。これは拡張カルマンフィルタでの計算と同様の考えになります。
\(x\) の平均ベクトル \( \bar{x} \) のまわりで \(h(x)\) を線形近似します。

\[\begin{split} \begin{align*} y &\simeq h(\bar{x}) + \left. \frac{\partial h }{\partial x} \right| _{\bar{x}} (x - \bar{x}) \\ &= h(\bar{x}) + \hat{H} (x - \bar{x}) \end{align*} \end{split}\]

\(h\) の \(\bar{x}\) におけるヤコビ行列を \(\hat{H}\) とおきました。線形近似した関数により \(y\) の平均ベクトルを計算します。

\[\begin{split} \begin{align*} \mathbb{E}[y] &\simeq \mathbb{E}\left[ h(\bar{x}) + \hat{H} (x - \bar{x}) \right] \\ &= h(\bar{x}) + \hat{H}~ \mathbb{E}\left[(x - \bar{x}) \right] \\ &= h(\bar{x}) \end{align*} \end{split}\]

これは \(x\) の平均ベクトルを \(h\) により変換することで、\(y\) の平均ベクトルが近似的に求まることを意味しています。
共分散行列は以下で近似されます。

\[\begin{split} \begin{align*} \mathbb{V}[y] &\simeq \mathbb{E}\left[ \{ h(\bar{x}) + \hat{H} (x - \bar{x}) - h(\bar{x}) \} \{ h(\bar{x}) + \hat{H} (x - \bar{x}) - h(\bar{x}) \}^T \right] \\ &= \hat{H}~ \mathbb{E}\left[(x - \bar{x}) (x - \bar{x})^T \right] \hat{H}^T \\ &= \hat{H} P_x \hat{H}^T \\ \end{align*} \end{split}\]
Hide code cell source 
def jacobian(x):
    return np.diag(0.5 + 0.5 * np.cos(x))


linearized_mu_y = nonlinear_transform(mu_x)
H_hat = jacobian(mu_x)
linearized_cov_y = H_hat @ cov_x @ H_hat.T
linearized_mu_y, linearized_cov_y

(array([0.        , 1.45464871]),
 array([[0.4       , 0.01167706],
        [0.01167706, 0.03408845]]))

それぞれの方法で計算した平均ベクトルと共分散行列を比較してみましょう。

Hide code cell source 
fig, ax = plt.subplots(1, 1, figsize=(6, 6))
ax.scatter(
    y[:, 0], y[:, 1], s=20, color="steelblue", edgecolor="none", alpha=0.2, label="y"
)

ax.scatter(
    sigma_point_y[:, 0],
    sigma_point_y[:, 1],
    s=50,
    color="gold",
    edgecolor="none",
    label="Sigma Point",
)

ax.scatter(mu_y[0], mu_y[1], s=50, color="red", edgecolor="none", label="Mean (All)")

ax.scatter(ut_mu_y[0], ut_mu_y[1], s=30, marker="x", color="gold", label="Mean (Sigma)")

ax.scatter(
    linearized_mu_y[0],
    linearized_mu_y[1],
    s=30,
    marker="x",
    color="violet",
    label="Mean (Linearize)",
)

width, height, angle = get_covariance_ellipse(cov_y)
ell = pat.Ellipse(
    xy=mu_y,
    width=width,
    height=height,
    angle=angle,
    edgecolor="red",
    fc="none",
    lw=2,
    alpha=0.8,
    label="Covariance (All)",
)
ax.add_patch(ell)

width, height, angle = get_covariance_ellipse(ut_cov_y)
ell = pat.Ellipse(
    xy=ut_mu_y,
    width=width,
    height=height,
    angle=angle,
    edgecolor="gold",
    fc="none",
    ls="-",
    lw=2,
    alpha=0.8,
    label="Covariance (Sigma)",
)
ax.add_patch(ell)

width, height, angle = get_covariance_ellipse(linearized_cov_y)
ell = pat.Ellipse(
    xy=ut_mu_y,
    width=width,
    height=height,
    angle=angle,
    edgecolor="violet",
    fc="none",
    lw=2,
    alpha=0.8,
    label="Covariance (Linearize)",
)
ax.add_patch(ell)
ax.set_xlabel("$y_1$")
ax.set_ylabel("$y_2$")
fig.legend(bbox_to_anchor=(0.9, 0.8), loc="upper left")

plt.show()
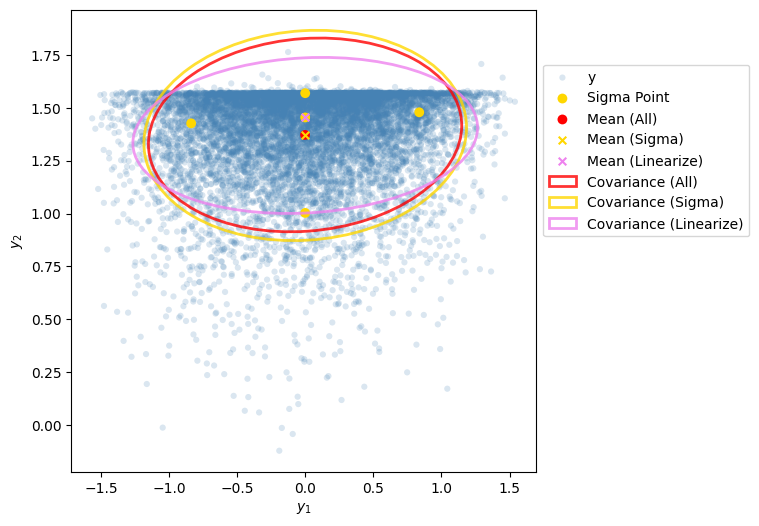
../_images/bcaff13ba8b061873d7aee3a0973322d105cffe9a61f3525c103ec99b4d9ec60.png

Mean(All)が変換後の全てのサンプル点から計算した平均ベクトル、Mean(Sigma)が変換後のシグマポイントから計算した平均ベクトル、Mean(Linearize)が線形近似した関数から計算した平均ベクトルです。 共分散行列についても同様です。僅か5点のシグマポイントをもとに計算した平均ベクトルと共分散行列は、全てのサンプル点から計算した平均ベクトルと共分散行列に近いことが分かります。 一方、非線形関数を線形近似し計算した平均ベクトルと共分散行列は、全てのサンプル点から計算したものから少し離れていることが分かります。

Unscentedカルマンフィルタ#

引き続きUnscentedカルマンフィルタについて説明します。非線形システムが以下の通り記述されるとします。

\[\begin{split} \begin{align*} x_{k+1} &= f_k(x_k) + w_k \\ y_k &= h_k(x_k) + v_k \\ \end{align*} \end{split}\]

拡張カルマンフィルタと同様に、\(w_k\) と \(v_k\) はそれぞれ平均 \(0\)、共分散行列 \(Q_k\) と \(R_k\) のガウス性の白色雑音であり、互いに独立とします。

\[\begin{split} \begin{align*} &w_k \sim \mathcal{N}(0, Q_{k}) \\ &v_k \sim \mathcal{N}(0, R_{k}) \\ % &\mathbb{E}[w_k] = 0\\ % &\mathbb{E}[v_k] = 0 \\ &\mathbb{E}[w_kw_s^T] = Q_k\delta_{ks} \\ &\mathbb{E}[v_kv_s^T] = R_k\delta_{ks} \\ &\mathbb{E}[v_kw_s^T] = 0, ~~k,s=0,1,\cdots \end{align*} \end{split}\]

雑音にガウス性を仮定するか否かは文献により異なるようですが、ここではガウス性を仮定している文献に従っています。 非線形関数がより一般的な \(f_k(x_k, w_k)\) や \(h_k(x_k, v_k)\) の形をとる場合、Unscentedカルマンフィルタのアルゴリズムはここで紹介するものよりも少し複雑になります。 この場合のアルゴリズムについては参考文献[3] [5]を参照下さい。

さて、Unscented変換により計算した平均ベクトルと共分散行列が、線形近似した関数から求めたものより良い近似となっていることを前節の例で見ました。 Unscentedカルマンフィルタのアルゴリズムは、拡張カルマンフィルタのアルゴリズムで行う平均ベクトルと共分散行列の計算を、Unscented変換による計算に置き換えたものになります。 そこで拡張カルマンフィルタの計算を、平均ベクトルと共分散行列の単位で整理してみます。

拡張カルマンフィルタにおける平均ベクトルと共分散行列の計算#

平均 / 共分散

記号

拡張カルマンフィルタでの計算

計算箇所

1

\( \mathbb{E}[x_{k}|Y_{k-1}] \)

\( \hat{x}_{k|k-1} \)

\(f_{k-1}(\hat{x}_{k-1|k-1})\)

予測ステップ

2

\(\mathbb{E}[\tilde{x}_{k|k-1}\tilde{x}_{k|k-1}^T|Y_{k-1}]\)
\(\tilde{x}_{k|k-1} \triangleq x_k - \hat{x}_{k|k-1}\)

\({P}_{k|k-1}\)

\(\hat{F}_{k-1} P_{k-1|k-1} \hat{F}_{k-1}^T + Q_{k-1}\)

予測ステップ

3

\(\mathbb{E}[y_k|Y_{k-1}]\)

\(\hat{y}_{k|k-1}\)

\(h_k(\hat{x}_{k|k-1})\)

観測更新ステップ

4

\(\mathbb{E}[\tilde{y}_{k|k-1}\tilde{y}_{k|k-1}^T|Y_{k-1}]\)
\(\tilde{y}_{k|k-1} \triangleq y_k - \hat{y}_{k|k-1}\)

\(V_{k|k-1}\)

\(\hat{H}_k P_{k|k-1} \hat{H}_k^T + R_k\)

観測更新ステップ

5

\(\mathbb{E}[\tilde{x}_{k|k-1}\tilde{y}_{k|k-1}^T|Y_{k-1}]\)

\(U_{k|k-1}\)

\(P_{k|k-1} \hat{H}_k^T\)

観測更新ステップ

6

\(\mathbb{E}[x_k|Y_k]\)

\(\hat{x}_{k|k}\)

\(\hat{x}_{k|k-1} + U_{k|k-1} V_{k|k-1}^{-1} (y_k - \hat{y}_{k|k-1})\)

観測更新ステップ

7

\(\mathbb{E}[\tilde{x}_{k|k}\tilde{x}_{k|k}^T|Y_{k}]\)
\(\tilde{x}_{k|k} \triangleq x_k - \hat{x}_{k|k}\)

\({P}_{k|k}\)

\({P}_{k|k-1} - U_{k|k-1} V_{k|k-1}^{-1} U_{k|k-1}^T\)

観測更新ステップ

平均 / 共分散の列には、アルゴリズムで登場する平均または共分散行列が表している量を書いています。 例えば1行目の \(\mathbb{E}[x_k|Y_{k-1}]\) は、\(p(x_k|Y_{k-1})\) の平均ベクトルの期待値記号による表記です。 2行目の \(\mathbb{E}[\tilde{x_k}\tilde{x_k}^T|Y_{k-1}]\) は、\(p(x_k|Y_{k-1})\) の共分散行列の期待値記号による表記です。 他についても同様です。

記号は、拡張カルマンフィルタのアルゴリズムで使われているものになります。但し、\(\hat{y}_{k|k-1}\)、\({V}_{k|k-1}\)、\(U_{k|k-1}\) はここで新たに定義したものです。

拡張カルマンフィルタでの計算の列には、平均 / 共分散の列に書いている項の拡張カルマンフィルタでの近似式を書いています。並びはアルゴリズムの手順に沿っています。 3行目から5行目は6行目と7行目に含まれる式になります。これらはそれぞれ \(\mathbb{E}[y_k|Y_{k-1}]\)、\(\mathbb{E}[\tilde{y}_k \tilde{y}_k^T|Y_{k-1}]\)、\(~\mathbb{E}[\tilde{x}_k \tilde{y}_k^T|Y_{k-1}]\) の近似式となっているのですが、詳細ついては省略します。興味のある方は参考文献[2] [6]を参照下さい。

上の表にUnscented変換による計算を追加し、拡張カルマンフィルタによる計算と対比したものが以下となります。

拡張カルマンフィルタとUnscentedカルマンフィルタにおける平均ベクトルと共分散行列の計算#

平均 / 共分散

記号

拡張カルマンフィルタでの計算

Unscentedカルマンフィルタでの計算

1

\( \mathbb{E}[x_{k}|Y_{k-1}] \)

\( \hat{x}_{k|k-1} \)

\(f_{k-1}(\hat{x}_{k-1|k-1})\)

\( \sum_{i=0}^{2n} W_m^{(i)} f_k(x_{k-1|k-1}^{(i)}) \)

2

\(\mathbb{E}[\tilde{x}_{k|k-1}\tilde{x}_{k|k-1}^T|Y_{k-1}]\)
\(\tilde{x}_{k|k-1} \triangleq x_k - \hat{x}_{k|k-1}\)

\({P}_{k|k-1}\)

\(\hat{F}_{k-1} P_{k-1|k-1} \hat{F}_{k-1}^T + Q_{k-1}\)

\( \sum_{i=0}^{2n} W_c^{(i)} (\hat{x}_{k|k-1}^{(i)} -\hat{x}_{k|k-1}) (\hat{x}_{k|k-1}^{(i)} -\hat{x}_{k|k-1})^T + Q_{k-1}\)

3

\(\mathbb{E}[y_k|Y_{k-1}]\)

\(\hat{y}_{k|k-1}\)

\(h_k(\hat{x}_{k|k-1})\)

\( \sum_{i=0}^{2n} W_m^{(i)} h_k(x_{k|k-1}^{(i)}) \)

4

\(\mathbb{E}[\tilde{y}_{k|k-1}\tilde{y}_{k|k-1}^T|Y_{k-1}]\)
\(\tilde{y}_{k|k-1} \triangleq y_k - \hat{y}_{k|k-1}\)

\(V_{k|k-1}\)

\(\hat{H}_k P_{k|k-1} \hat{H}_k^T + R_k\)

\( \sum_{i=0}^{2n} W_c^{(i)} (\hat{y}_{k|k-1}^{(i)} -\hat{y}_{k|k-1}) (\hat{y}_{k|k-1}^{(i)} -\hat{y}_{k|k-1})^T + R_k\)

5

\(\mathbb{E}[\tilde{x}_{k|k-1}\tilde{y}_{k|k-1}^T|Y_{k-1}]\)

\(U_{k|k-1}\)

\(P_{k|k-1} \hat{H}_k^T\)

\( \sum_{i=0}^{2n} W_c^{(i)} (\hat{x}_{k|k-1}^{(i)} -\hat{x}_{k|k-1}) (\hat{y}_{k|k-1}^{(i)} -\hat{y}_{k|k-1})^T \)

6

\(\mathbb{E}[x_k|Y_k]\)

\(\hat{x}_{k|k}\)

\(\hat{x}_{k|k-1} + U_{k|k-1} V_{k|k-1}^{-1} (y_k - \hat{y}_{k|k-1})\)

同左

7

\(\mathbb{E}[\tilde{x}_{k|k}\tilde{x}_{k|k}^T|Y_{k}]\)
\(\tilde{x}_{k|k} \triangleq x_k - \hat{x}_{k|k}\)

\({P}_{k|k}\)

\({P}_{k|k-1} - U_{k|k-1} V_{k|k-1}^{-1} U_{k|k-1}^T\)

同左

Unscentedカルマンフィルタでの計算列の、 \(\hat{x}^{(i)}_{k-1|k-1}\) は \(\hat{x}_{k-1|k-1}\) を中心に生成したシグマポイント、\(\hat{x}^{(i)}_{k|k-1}\) は \(\hat{x}_{k|k-1}\) を中心に生成したシグマポイントを表しています。 また \(y^{(i)}_{k|k-1} = h_k(\hat{x}^{(i)}_{k|k-1})\) です。

この列の1行目から5行目の計算式は、雑音の共分散行列が考慮されていることを除き、平均/共分散列に書いている項をUnscented変換で計算したものになっていることが分かります。 6行目と7行目は5行目までの結果を代入して計算されます。

拡張カルマンフィルタのアルゴリズムで行う平均ベクトルと共分散行列の計算を、上の表のUnscented変換による計算に置き換えると、Unscentedカルマンフィルタのアルゴリズムが得られます。 シグマポイントと重みの計算も含めるとアルゴリズムは以下となります。 状態の初期値の設定部分は拡張カルマンフィルタと同じであるため省略します。

Unscentedカルマンフィルタのアルゴリズム#

Unscentedカルマンフィルタのアルゴリズム

  • 重みの計算

    \[\begin{split} \begin{align*} \lambda &= \alpha^2 (n + \kappa) - n \\ W_m^{(0)} &= \frac{\lambda}{n + \lambda} \\ W_c^{(0)} &= \frac{\lambda}{n + \lambda} + 1 - \alpha^2 + \beta\\ W_m^{(i)} &= \frac{1}{2(n + \lambda)}~, ~i=1,\cdots, 2n \\ W_c^{(i)} &= \frac{1}{2(n + \lambda)}~, ~i=1,\cdots, 2n \\ \end{align*} \end{split}\]

\( k=1,2 \cdots \) に対して以下を繰り返します。

  • 予測ステップ

    • シグマポイントの計算

      \[\begin{split} \begin{align*} \hat{x}^{(0)}_{k-1|k-1} &= \hat{x}_{k-1|k-1} \\ \hat{x}^{(i)}_{k-1|k-1} &= \hat{x}_{k-1|k-1} + \sqrt{n + \kappa} (\sqrt{P_{k-1|k-1}})_{i} ~, ~~~ i=1,\cdots n \\ \hat{x}^{(n+i)}_{k-1|k-1} &= \hat{x}_{k-1|k-1} - \sqrt{n + \kappa} (\sqrt{P_{k-1|k-1}})_{i} ~, ~~~ i=1,\cdots n \\ \end{align*} \end{split}\]

    • シグマポイントの変換

      \[ \begin{align*} \hat{x}^{(i)}_{k|k-1} &= f_{k-1}(\hat{x}^{(i)}_{k-1|k-1}) ~, ~~~ i=0,\cdots, 2n \end{align*} \]

    • \( \hat{x}_{k|k-1},~ P_{k|k-1} \) の計算

      \[\begin{split} \begin{align*} \hat{x}_{k|k-1} &= \sum_{i=0}^{2n} W_m^{(i)} \hat{x}^{(i)}_{k|k-1}　\\ P_{k|k-1} &= \sum_{i=0}^{2n} W_c^{(i)} (\hat{x}^{(i)}_{k|k-1}-\hat{x}_{k|k-1}) (\hat{x}^{(i)}_{k|k-1}-\hat{x}_{k|k-1})^T + Q_{k-1} \end{align*} \end{split}\]

  • 観測更新ステップ

    • シグマポイントの計算

      \[\begin{split} \begin{align*} \hat{x}^{(0)}_{k|k-1} &= \hat{x}_{k|k-1} \\ \hat{x}^{(i)}_{k|k-1} &= \hat{x}_{k|k-1} + \sqrt{n + \lambda} (\sqrt{P_{k|k-1}})_{i} ~, ~~~ i=1,\cdots n \\ \hat{x}^{(n+i)}_{k|k-1} &= \hat{x}_{k|k-1} - \sqrt{n + \lambda} (\sqrt{P_{k|k-1}})_{i} ~, ~~~ i=1,\cdots n \\ \end{align*} \end{split}\]

    • シグマポイントの変換

      \[ \begin{align*} y^{(i)}_{k|k-1} &= h_k(\hat{x}^{(i)}_{k|k-1}) ~, ~~~ i=0,\cdots, 2n \end{align*} \]

    • \( \hat{x}_{k|k},~ P_{k|k} \) の計算

      \[\begin{split} \begin{align*} \hat{y}_{k|k-1} &= \sum_{i=0}^{2n} W_m^{(i)} y^{(i)}_{k|k-1} \\ V_{k|k-1} &= \sum_{i=0}^{2n} W_c^{(i)} (y^{(i)}_{k|k-1}-\hat{y}_{k|k-1}) (y^{(i)}_{k|k-1}-\hat{y}_{k|k-1})^T + R_k \\ U_{k|k-1} &= \sum_{i=0}^{2n} W_c^{(i)} (\hat{x}^{(i)}_{k|k-1}-\hat{x}_{k|k-1}) (y^{(i)}_{k|k-1}-\hat{y}_{k|k-1})^T \\ K_k &= U_{k|k-1} V_{k|k-1}^{-1} \\ \hat{x}_{k|k} &= \hat{x}_{k|k-1} + K_k (y_k - \hat{y}_{k|k-1}) \\ P_{k|k} &= P_{k|k-1} - U_{k|k-1} V_{k|k-1}^{-1} U_{k|k-1}^T \end{align*} \end{split}\]

Unscentedカルマンフィルタは拡張カルマンフィルタよりも非線形性に強く性能が良いとされています。またヤコビ行列の計算が不要であるため拡張カルマンフィルタに比べ実装も容易です。


CSTRの状態推定#

具体的なモデルに対し、非線形カルマンフィルタで状態を推定してみましょう。
非線形カルマンフィルタの実装はpykalmanものを利用します。 本稿執筆時点でpykalmanにUnscentedカルマンフィルタは実装されている一方、拡張カルマンフィルタは実装されていません。 本来は非線形カルマンフィルタ毎に推定精度を比較できると良いのですが、今回はUnscentedカルマンフィルタのみを用います。利用したpykalmanのバージョンは0.10.2です。

状態推定の対象は連続撹拌槽型反応器（continuous stirred tank reactor: CSTR）の非線形モデルとします[7] [8]。 CSTRは化学プラントにおいて利用される反応器の一種です。 CSTRモデルを利用したシミュレーションデータから、UnscentedカルマンフィルタによりCSTRの状態を推定します。
モデルの概要について説明します。 成分Aを含む原料が連続的に反応器内に流入し、反応器内で攪拌されながら発熱を伴う不可逆の化学反応が起こります。これにより反応器内の成分Aの一部がBに変化し、反応器から流出されます。 反応器外側にはジャケットが付いており、ジャケット温度を制御することで反応器内の温度を制御します。 一般にジャケット温度はジャケット内部を流れる冷却水などの熱媒体により制御されますが、この部分のダイナミクスについては考慮していないモデルになります。

cstr

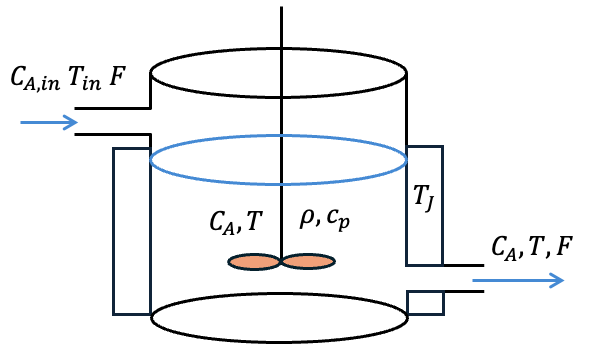
微分方程式と各変数の意味は以下の通りです。

\[\begin{split} \begin{align*} V \frac{dC_A}{dt} &= F (C_{A,in} - C_A) - V k C_A \\ \rho c_p V \frac{dT}{dt} &= \rho c_p F (T_{in} - T) +(-\Delta h_{r}) V k C_A + A U(T_J-T) \\ k & = k_0 ~\mathrm{exp} (\frac{-E}{RT}) \\ \end{align*} \end{split}\]

  • \(C_{A,in}\) : 流入する原料の成分Aの濃度 [mol/L]

  • \(T_{in}\) : 流入温度 [K]

  • \(F\) : 流入流量 [L/min]

  • \(C_A\) : 反応器内の成分Aの濃度 [mol/L]

  • \(T\) : 反応器内の温度 [K]

  • \(V\) : 反応器内の物質の体積 [L]

  • \(\rho\) : 反応器内の物質の密度 [g/L]

  • \(c_p\) : 反応器内の物質の比熱 [J/(g·K)]

  • \(k\) : 反応速度定数 [1/min]

  • \(\Delta h_r\) : 反応熱 [J/mol]

  • \(E\) : 活性化エネルギー [J/mol]

  • \(R\) : 気体定数 [J/(mol·K)]

  • \(A\) : 伝熱面積 [m\(^2\)]

  • \(U\) : 総括伝熱係数 [J/(min·m\(^2·\)K)]

  • \(T_J\) : ジャケット温度 [K]

状態変数は反応器内の温度 \(T\) と濃度 \(C_A\) になります。上の2つの微分方程式が状態方程式となりますが、連続時間で表現されています。 本稿で解説したUnscentedカルマンフィルタを適用するには離散時間の状態方程式が必要なため、実装の際にルンゲ・クッタ法で離散化します。 観測変数は温度のみとします。つまり濃度が観測でない状況で、雑音を含む温度観測値からUnscentedカルマンフィルタで温度と濃度の両方を推定します。 またジャケット温度 \(T_J\) を外部から操作できる変数、つまり制御入力 \(u\) とします。反応器外側のジャケット温度を操作することで、反応器内の温度と濃度が変化します。 状態方程式に制御入力（外部入力）が含まれる場合のカルマンフィルタのアルゴリズムの変更点は、アルゴリズム内で利用する状態方程式を制御入力を含む形にするのみとなります。
それではCSTRモデルを実装します。パラメータはSeborg[7]のものを採用します。

Hide code cell source 
class CSTR:
    def __init__(self, dt=0.1):

        self.F = 100  # [L/min]
        self.T_in = 350  # [K]
        self.CA_in = 1.0  # [mol/L]

        self.V = 100  # [L]
        self.rho = 1000  # [g/L]
        self.cp = 0.239  # [J/g·K]

        self.E_over_R = 8750  # [K]
        self.k0 = 7.2e10  # [1/min]
        self.delta_H = -5e4  # [J/mol]

        self.AU = 5e4  # [J/min·m^2·K]

        self.u = None
        self.dt = dt

    def set_input(self, u):
        self.u = u

    def state_equation_continuous(self, state):

        CA, T = state[0], state[1]
        Tj = self.u
        k = self.k0 * np.exp(-self.E_over_R / (T + 1e-10))
        kca = k * CA

        dCA_dt = (self.F / self.V) * (self.CA_in - CA) - kca
        dT_dt = (
            (self.F / self.V) * (self.T_in - T)
            - self.delta_H * kca / (self.rho * self.cp)
            + (self.AU / (self.V * self.rho * self.cp)) * (Tj - T)
        )

        return np.array([dCA_dt, dT_dt])

    def _state_equation_rk4(self, state):

        dt = self.dt
        k1 = self.state_equation_continuous(state)
        k2 = self.state_equation_continuous(state + 0.5 * dt * k1)
        k3 = self.state_equation_continuous(state + 0.5 * dt * k2)
        k4 = self.state_equation_continuous(state + dt * k3)
        state_next = state + (dt / 6) * (k1 + 2 * k2 + 2 * k3 + k4)

        return state_next

    def state_equation(self, state):
        return self._state_equation_rk4(state)

    def observation_equation(self, state):
        Ca, T = state[0], state[1]
        return np.array([T])

実装したCSTRクラスの state_equation メソッドがルンゲ・クッタ法により離散化した状態方程式になります。
state_equation と observation_equation メソッドは、今回利用するpykalmanの AdditiveUnscentedKalmanFilter クラスが受け取る状態方程式と観測方程式のインターフェースに合わせるため、状態のみを引数に取る形で実装しています。

CSTRオブジェクトを作成します。
サンプリング周期は \(0.05\) minに、また時間応答を計算する際に加える駆動雑音 \(w_k\) と 観測雑音 \(v_k\) の分散 \(Q\) と \(R\) は以下の値にしました。

\[\begin{split} \begin{align*} &Q = \begin{bmatrix} 2e^{-5} & 0 \\ 0 & 0.1 \end{bmatrix} ~, ~~~ R = 1 \\ \end{align*} \end{split}\]

今回のシミュレーションでは時刻 \(k\) に依らず一定の値とするため、添字 \(k\) を省略し \(Q\) と \(R\) と表記しています。

dt = 0.05
cstr = CSTR(dt=dt)

Q = np.diag([2e-5, 0.1])
R = np.diag([1])

カルマンフィルタでCSTRの状態を推定する前に、まずはCSTRのダイナミクスを確認しましょう。 反応器内の濃度と温度の初期値を適当に \(C_A = 0.5\) mol/L、\(T = 350\) K とし、その状態でジャケット温度を \(T_J = 280 \) Kに保った場合の時間応答を計算します。

np.random.seed(1)

timepts = np.arange(0, 20, dt)
CA0, T0, Tj = 0.5, 350, 280

states = np.zeros((timepts.shape[0], 2))
observations = np.zeros((timepts.shape[0], 1))
states[0] = np.array([CA0, T0])
cstr.set_input(Tj)  # 制御入力であるジャケット温度を設定

# 状態方式と観測方程式を繰り返し計算
for k in range(timepts.shape[0]):
    if k > 0:
        states[k] = cstr.state_equation(states[k - 1]) + np.random.multivariate_normal(
            np.zeros(2), Q
        )
    observations[k] = cstr.observation_equation(
        states[k]
    ) + np.random.multivariate_normal(np.zeros(1), R)

fig, axes = plt.subplots(3, 1, figsize=(8, 8), sharex=True)
axes[0].plot(timepts, states[:, 0], color="steelblue", label="$C_A (truth)$")
axes[0].set_ylabel("Concentration [mol/L]")
axes[0].set_xlabel("Time [min]")

axes[1].plot(timepts, observations[:, 0], color="goldenrod", label="$T ~(observed)$")
axes[1].plot(timepts, states[:, 1], color="steelblue", label="$T ~(truth)$")
axes[1].set_ylabel("Reactor tempreture [K]")
axes[1].set_xlabel("Time [min]")

axes[2].plot(timepts, np.full(timepts.shape[0], Tj), color="steelblue", label="$T_j$")
axes[2].set_ylabel("Jacket temperature [K]")
axes[2].set_xlabel("Time [min]")

for ax in axes:
    ax.grid(True)
    ax.legend()
plt.show()

last_state = states[-1]
last_obs = observations[-1]
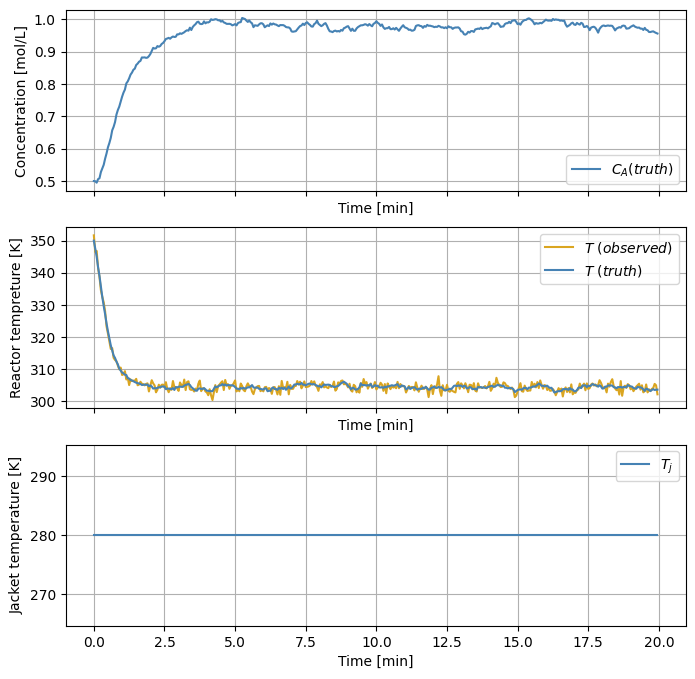
../_images/ebcef9262e48ab5f2cc00b528f1e606b864e0d20bd8be9c93d82fc6968b73212.png

truthと表記されている波形が真の状態、observedと表記されている波形がその観測値です。 今回のCSTRモデルでは反応器内の温度が高くなるほど発熱反応が進み、物質Aの濃度は下がります。逆に、反応器内の温度が下がると物質Aの濃度は上がります。 上のシミュレーションでは、ジャケット温度により反応器内の温度が下がったため、濃度は上昇する結果となりました。

さて、上の時間応答の最後の状態を新たな初期値とし、ジャケット温度を上げて \(300\) Kに設定します。その際の反応器内の温度と濃度をUnscentedカルマンフィルタにより推定してみましょう。
まずはAdditiveUnscentedKalmanFilterオブジェクトを作成します。

import pykalman

ukf = pykalman.AdditiveUnscentedKalmanFilter(
    transition_functions=cstr.state_equation,
    observation_functions=cstr.observation_equation,
    transition_covariance=Q,
    observation_covariance=R,
)

カルマンフィルタを適用するには対象の状態方程式と観測方程式が必要なため、ここではこれらが既知であるとしてCSTRオブジェクトのメソッドを与えています。 また雑音の共分散行列 \(Q\) と \(R\) も今回は既知であるとし真の値を与えていますが、実際には調整するパラメータになります。 観測雑音の共分散行列 \(R\) については実際のセンサ特性などを考慮して決定すると良いようです[9]。

推定する状態と共分散行列の初期値も必要となります。 状態変数は濃度と温度の2つでした。濃度の初期値は \(1\) と設定し、温度の初期値は観測値をそのまま利用しました。 共分散行列の初期値は \(\text{diag}(0.05,~ 3)\) としました。
それではUnscentedカルマンフィルタによりCSTRの状態を推定します。

timepts = np.arange(0, 30, dt)

# CSTRの状態と観測値の時系列を格納する変数の初期化
states = np.zeros((timepts.shape[0], 2))
observations = np.zeros((timepts.shape[0], 1))
states[0] = last_state  # 前回の最後の状態を初期値に
observations[0] = last_obs  # 前回の最後の観測値を初期値に

# 状態推定値とその共分散行列を格納する時系列の初期化
states_est = np.zeros_like(states)
covariances_est = np.zeros((timepts.shape[0], 2, 2))
states_est[0] = np.array([1, last_obs[0]])
covariances_est[0] = np.diag([0.05, 3])

update_cnt = set([int(10 / dt)])
Tj = 280
inputs = []

# 状態推定のシミュレーション
for k in range(1, timepts.shape[0]):

    # ジャケット温度を上げる
    if k in update_cnt:
        Tj += 20

    # 制御入力となるCSTRのジャケット温度を設定
    cstr.set_input(Tj)
    inputs.append(Tj)

    # CSTRの状態を1ステップ進めて観測値を取得
    states[k] = cstr.state_equation(states[k - 1]) + np.random.multivariate_normal(
        [0, 0], Q
    )
    observations[k] = cstr.observation_equation(
        states[k]
    ) + np.random.multivariate_normal([0], R)

    # Unscentedカルマンフィルタにより状態を推定
    states_est[k], covariances_est[k] = ukf.filter_update(
        filtered_state_mean=states_est[k - 1],
        filtered_state_covariance=covariances_est[k - 1],
        observation=observations[k],
    )

fig, axes = plt.subplots(3, 1, figsize=(8, 9), sharex=True)
axes[0].plot(timepts, states[:, 0], color="steelblue", label="$C_A (truth)$")
axes[0].plot(
    timepts, states_est[:, 0], "--", color="violet", label="$C_A ~(estimated)$"
)
axes[0].set_ylabel("Concentration [mol/L]")
axes[0].set_xlabel("Time [min]")

axes[1].plot(timepts, observations[:, 0], color="goldenrod", label="$T ~(observed)$")
axes[1].plot(timepts, states[:, 1], color="steelblue", label="$T ~(truth)$")
axes[1].plot(timepts, states_est[:, 1], "--", color="violet", label="$T ~(estimated)$")
axes[1].set_ylabel("Reactor temperature [K]")
axes[1].set_xlabel("Time [min]")

axes[2].plot(timepts[:-1], np.array(inputs), color="steelblue", label="$T_J$")
axes[2].set_ylabel("Jacket temperature [K]")
axes[2].set_xlabel("Time [min]")

for ax in axes:
    ax.grid(True)
    ax.legend()
plt.show()
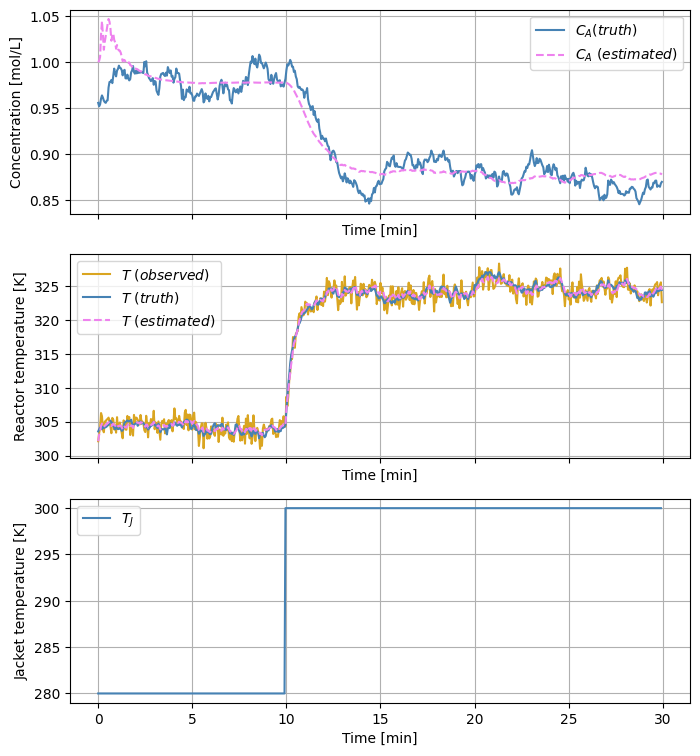
../_images/5e5a9a0261b52b66b64ebbac00bce700d30d7c1b21f94b3371f3bb7bed28c76d.png

truthと表記している波形が真の状態、estimatedと表記している波形が状態の推定値になります。 状態推定を開始して10分の時点でジャケット温度を \(300\) Kに上げています。反応器外側のジャケット温度が上がったため反応器内の温度も上昇し、化学反応が進み濃度は下がっています。 観測値は反応器内の温度のみです。 状態推定開始直後の濃度の推定値はやや乱れていますが、その後はジャケット温度を変更した直後も含め、反応器内の濃度と温度を良好に推定できているように見えます。

小括#

本稿では、非線形システムのためのカルマンフィルタである拡張カルマンフィルタとUnscentedカルマンフィルタについて解説しました。 具体的には、まず状態方程式の線形性とガウス性のいずれかが満たされない場合、条件付き確率分布を厳密に求めることができず、非線形カルマンフィルタでは何らかの近似が必要になることを解説しました。 そして、非線関数を線形近似しヤコビ行列を利用することで拡張カルマンフィルタのアルゴリズムが得られること、 平均ベクトルと共分散行列の計算をUnscented変換により行うことでUnscentedカルマンフィルタのアルゴリズムが得られることを解説しました。 最後に、CSTRモデルに対しUnscentedカルマンフィルタを適用し、状態推定のシミュレーションを行いました。

著者情報

水野 貴志 (Mizuno, Takashi)

  • イノベーションセンター　テクノロジー部門　先端AI数理PJ

参考文献#

目次