用語集（か行）

用語集（か行）#

か#

カイ二乗分布#

  • 読み: かいにじょうぶんぷ

  • 英語での表現: chi-square distribution

  • Tags: 確率・統計

\(Z_1,\ldots,Z_k\)が互いに独立で標準正規分布\(N(z;0,1)\)に従う確率変数とした場合に、自由度\(k\)の\(X=\sum_{i=1}^kZ_i^2\)が従う確率分布\(\chi^2(x;k)(=Ga(x;k/2,1/2))\)。

確率密度関数

\[ f \left( x; k \right) =\frac{1}{2^{\frac{k}{2}}\Gamma\left(\frac{k}{2}\right)}x^{\frac{k}{2}-1}\exp\left(-\frac{x}{2}\right) \]

ただし\(\Gamma(\alpha)\)はガンマ関数で

\[ \Gamma(\alpha)=\int_0^{\infty}t^{\alpha-1}\exp(-t)dt \]

モーメント母関数

\[ M_X(t)=\left(\frac{1}{1-2t}\right)^{\frac{k}{2}} \]

期待値

\[ E[X]=k \]

分散

\[ V[X]=2k \]

再生性
互いに独立な\(X_i\sim \chi^2(x;k_i)\)について

\[ X_1+X_2\sim \chi^2(x;k_1+k_2) \]

正規分布に従う母集団を用いた検定
確率変数\(Y_1,\ldots,Y_k\)が互いに独立に正規分布\(N(y;\mu,\sigma^2)\)に従うとき、次の確率変数\(X\)は自由度\(k\)のカイ二乗分布に従う。

\[ X=\sum_{i=1}^k\left(\frac{Y_i-\mu}{\sigma}\right)^2\sim\chi^2(x;k) \]

また、この式を展開して得られる次の確率変数\(X\)は自由度\(k-1\)のカイ二乗分布に従う。

\[ X=\sum_{i=1}^k\left(\frac{Y_i-\bar{Y}}{\sigma}\right)^2=\frac{(k-1)S^2}{\sigma^2}\sim\chi^2(x;k-1) \]

ここで\(\bar{Y}\)は標本平均を\(S^2\)は不偏分散を意味する。

確率#

  • 読み: かくりつ

  • 英語での表現: probability

  • Tags: 確率・統計

ある出来事の起こりやすさを0から1の間の数値として表したもの。

現代数学（公理的確率論）においては

  1. 「確率を測れる出来事」である 事象 (event) \(E\) の集まり \(\mathcal{F}\) を適切に導入し、

  2. 考えているすべての事象 \(E\) に対して矛盾なく0から１の値を与える関数として 確率測度 (probability measure) \(P: \mathcal{F} \to [0, 1]\) を導入し、

  3. それぞれの事象 \(E\) に対する確率測度の値 \(P ( E )\) を確率とする

という手順で抽象的に定義される。このとき事象 \(E\) は適当な空間 \(\Omega\) （ 標本空間 (sample space) と呼ばれる）の部分集合となるように与えられて、事象同士の合併 \(\bigcup_{i \in \mathcal{I}} E_i\) （ \(\mathcal{I}\) は可算集合）や各事象の補集合 \(\Omega \setminus E\) もまた事象となる（確率を測ることができる）ように事象の集まりを \(\mathcal{F}\) を導入する。さらに、関数 \(P\) は次の性質

  • 各 \(E_i \cap E_j = \emptyset\) （ \(i, j \in \mathcal{I}\) ）のとき \(P ( \bigcup_{i \in \mathcal{I}} E_i ) = \sum_{i \in \mathcal{I}} P ( E_i )\)

    • 直感的には、事象が分割できるとき全体の確率は分割した各事象の確率の合計になるということ

  • \(P ( \Omega ) = 1\)

    • 標本空間全体の確率は1

を満たすように定めるものとする。確率とはこの3つ組 \(( \Omega, \mathcal{F}, P )\) （ 確率空間 (probability space) と呼ぶ）によって各事象 \(E\) に対して定まる値である。

確率論の議論において、これらの定義は確率変数を定義し、さらにさまざまな性質を持つ確率分布を具体的に、かつ数学的に正確に構成するための道具立てとして用いられる。

例: コイン投げ

例えばコイン投げを現代数学の方法で抽象化すると次のようになる。標本空間 \(\Omega = \{ \mathrm{H}, \mathrm{T} \}\) に対して事象の集まり \(\mathcal{F}\) を

\[ \mathcal{F} = \{ \emptyset, \{ \mathrm{H} \}, \{ \mathrm{T} \}, \Omega \} \]

として定める。直感的には、上で列挙した \(\mathcal{F}\) の要素（事象）はそれぞれ「表も裏も出ない」「表 (head) が出る」「裏 (tail) が出る」「表か裏が出る」という出来事に対応すると考える。この \(\mathcal{F}\) に対して、関数 \(P\) を

\[ P ( \emptyset ) = 0, \; P ( \{ \mathrm{H} \} ) = 0.5, \; P ( \{ \mathrm{T} \} ) = 0.5, \; P ( \Omega ) = 1 \]

として定めればこれは確率測度の条件を満たしており、例えば \(P ( \{ \mathrm{H} \} )\) は「コイン投げをして表が出る確率」として解釈することができる。もちろんこの \(( \Omega, \mathcal{F} )\) の組に対して別の確率測度を入れることもできて、例えば

\[ P' ( \emptyset ) = 0, \; P' ( \{ \mathrm{H} \} ) = 0.6, \; P' ( \{ \mathrm{T} \} ) = 0.4, \; P' ( \Omega ) = 1 \]

なる関数 \(P'\) も確率測度の条件を満たしており、これは表が裏よりも1.5倍出やすいコインを使った不公平なコイン投げを抽象化したものと解釈することができる。


例：単位区間上の一様乱数

同様に、0以上1以下の実数値をランダムに取る乱数については標本空間 \(\Omega = [0, 1]\) 、事象の集まり \(\mathcal{F}\) として区間 \([0, 1]\) 上のルベーグ可測な集合の集まり、確率測度 \(P\) として標準ルベーグ測度 \(\lambda\) を与えることで数学的に抽象化できる。このとき、ルベーグ測度の性質により1点 \(\omega \in [0, 1]\) のみからなる事象については \(P ( \{ \omega \} ) = \lambda ( \{ \omega \} ) = 0\) となるので、この乱数がある特定の値 \(\omega\) を取る確率は常に0として抽象化されることに注意が必要となる。


確率関数#

  • 読み: かくりつかんすう

  • 英語での表現: probability function

  • Tags: 確率・統計

離散確率分布に従う確率変数 \(X: \Omega \to \mathbf{R}\) の値域を \(\mathcal{X}\) （定義より高々可算）とおいたとき、 \(X\) がそれぞれの \(x \in \mathcal{X}\) を値に取る確率を表した関数

\[ f ( x ) = P ( X = x ) \]

を確率関数と呼ぶ。連続確率分布の確率密度関数と対比する場合にはしばしば 確率質量関数 (probability mass function, PMF) とも呼ばれる。確率関数は対応する離散確率分布を完全に特徴づける。

定義より、明らかに

\[ \sum_{x \in \mathcal{X}} f ( x ) = 1 \]

となる。また、対応する累積分布関数 \(F ( x )\) は

\[ F ( x ) = \sum_{x' : x' \le x} f ( x' ) \]

と表すことができる。

確率分布#

  • 読み: かくりつぶんぷ

  • 英語での表現: probability distribution

  • Tags: 確率・統計

確率変数 \(X\) がそれぞれの実現値 \(x\) を取る確率を表現したものを確率分布と呼ぶ。

数学的には、標本空間 \(\Omega\) と事象の集まり \(\mathcal{F}\) の上に定まった確率測度 \(P\) を（関数としての）確率変数 \(X: \Omega \to \mathbf{R}\) で実数 \(\mathbf{R}\) 上に押し出した測度 \(P_X\) を確率分布と同一視する。直感的には

  • 関数 \(X\) の値域 \(\mathcal{X}\) （ \(\mathcal{X} \subset \mathbf{R}\) ）の部分集合から「確率を測れるもの」をうまく集めてきて \(\mathcal{S}\) とおき、

  • \(\mathcal{S}\) の要素を \(X\) によって \(\mathcal{F}\) の要素と対応させ、

  • \(P\) によって測った \(\mathcal{F}\) の要素の確率から \(\mathcal{S}\) の要素の確率を定める

という手続きで \(P_X: \mathcal{S} \to [0, 1]\) を定めている（後述の具体例も参照）。

確率分布が適切に定まるとき、3つ組 \(( \mathcal{X}, \mathcal{S}, P_X )\) は元々の3つ組 \(( \Omega, \mathcal{F}, P )\) と共通の性質を持っている（確率空間になっている）。特に、 \(P_X\) で \(\mathcal{S}\) の要素を測った値は確率の定義を満たしている（即ち \(P_X\) は確率測度である）。確率論の議論ではこれら \(P_X\) のふるまいに主な興味があるため、確率分布 \(P_X\) と元の確率測度 \(P\) との具体的な関係には（そのような \(P_X\) が構成できることさえ示せれば）ほとんど興味が払われない。

離散確率変数（値域 \(\mathcal{X}\) が高々可算な確率変数）の確率分布を 離散確率分布 (discrete probability distribution) と呼ぶ。また、連続確率変数（値域 \(\mathcal{X}\) が非可算な確率変数）の確率分布のうちで対応する累積分布関数が連続なものを 連続確率分布 (continuous probability distribution) と呼ぶ。

例：コイン投げ （確率変数の項目の例の続き）

例えば公平なコイン投げの例　\(\Omega = \{ \mathrm{H}, \mathrm{T} \}\); \(P ( \{ \mathrm{H} \} ) = P ( \{ \mathrm{T} \} ) = 0.5\); \(X ( H ) = 1, X ( T ) = 0\) において離散確率変数 \(X\) の確率分布は、

\[\begin{split} \begin{align} P_X ( \{ x; X = x \} ) & = P ( \{ \omega; X ( \omega ) = x \} ) \\ & = \begin{cases} P ( \{ \omega; \omega \in \{ \mathrm{H} \} \} ), & x = 1 \\ P ( \{ \omega; \omega \in \{ \mathrm{T} \} \} ), & x = 0 \end{cases} \\ & = \begin{cases} 0.5, & x = 1 \\ 0.5, & x = 0 \end{cases} \end{align} \end{split}\]

によって定まる関数 \(P_X\) で表現できる。このとき \(\mathcal{X} = \{ 0, 1 \}\) であり、 \(\mathcal{S} = \{ \emptyset, \{ 0 \}, \{ 1 \}, \mathcal{X} \}\) としている。今回の例では、 \(P_X\) は成功確率のパラメータが \(p = 0.5\) のベルヌーイ分布になっている。


例：単位区間上の一様乱数 （確率変数の項目の例の続き）

同様に、0以上1以下の実数値をランダムに取る乱数の例　\(\Omega = [0, 1]\), \(P ( E ) = \lambda ( E )\) （ \(\lambda\) は標準ルベーグ測度）, \(X ( \omega ) = \omega\) において連続確率変数 \(X\) の確率分布は

\[\begin{split} \begin{align} P_X ( \{ x; X = x, a \le x \le b \} ) & = P ( \{ \omega; a \le X ( \omega ) \le b \} ) \\ & = \lambda ( \{ \omega; a \le \omega \le b \} ) \\ & = b - a \end{align} \end{split}\]

によって定まる関数 \(P_X\) で表現できる（ただし \(0 \le a \le b \le 1\) とする）。このとき \(\mathcal{X} = [0, 1]\) であり、 \(\mathcal{S} = \mathcal{F}\) としている。ルベーグ測度の性質により任意の \(x \in [0, 1]\) について \(P_X ( \{ x; X = x \} ) = \lambda ( \{ \omega; \omega = x \} ) = 0\) となるので、 \(X\) が特定の値を取る確率は常に0として定められていることに注意が必要となる。今回の例では、 \(P_X\) は区間 \([0, 1]\) 上の連続一様分布になっている。

一方、離散確率変数 \(Y ( \omega ) = 1_{\omega \ge 0.5}\) の確率分布は

\[\begin{split} \begin{align} P_Y ( \{ y; Y = y \} ) & = P ( \{ \omega; Y ( \omega ) = y \} ) \\ & = \begin{cases} \lambda ( \{ \omega; \omega \ge 0.5 \} ), & y = 1 \\ \lambda ( \{ \omega; \omega < 0.5 \} ), & y = 0 \end{cases} \\ & = \begin{cases} 0.5, & y = 1 \\ 0.5, & y = 0 \end{cases} \end{align} \end{split}\]

によって定まる関数 \(P_Y\) で表現できる。今回の例では、 \(P_Y\) は成功確率のパラメータが \(p = 0.5\) のベルヌーイ分布になっている。


関連項目

確率変数#

  • 読み: かくりつへんすう

  • 英語での表現: random variable

  • Tags: 確率・統計

確率の定義で現れた標本空間 \(\Omega\) から実数への関数 \(X: \Omega \to \mathbf{R}\) を確率変数と呼び、特定の元 \(\omega \in \Omega\) を与えたときの確率変数の値 \(x = X ( \omega )\) を確率変数の 実現値 (realization) と呼ぶ。確率論での慣例として、確率変数そのものは英字の大文字で、その実現値は対応する小文字で表すことが多い。また、標本空間に興味がないときは引数を省略して単に \(X = x\) などとも書く。

実現値の集合が可算である場合（有限の場合か、自然数や整数に対応する場合）は 離散確率変数 (discrete random variable) と呼ぶ。そうでない場合は 連続確率変数 (continuous random variable) と呼ぶ。確率が \(\Omega\) の部分集合 \(E \subset \Omega\) を取る関数であったのに対し、確率変数は \(\Omega\) の元 \(\omega \in \Omega\) を取る関数であることに注意が必要となる。

直感的には、確率変数 \(X\) は計算機上で擬似乱数を生成する手続きのようなもの、標本空間の元 \(\omega\) はそのシード値のようなものと考えることもできる。確率論の議論では \(X\) の実現値がそれぞれの値を取る確率（即ち \(X\) の確率分布）のふるまいに主な興味があるため、関数 \(X ( \omega )\) の具体的な形には（そのような関数 \(X\) が構成できることさえ示せれば）ほとんど興味が払われない。

例：コイン投げ （確率の項目の例の続き）

例えばコイン投げの例 \(\Omega = \{ \mathrm{H}, \mathrm{T} \}\) において、「表が出たら1円、裏が出たら0円を得る」という賭けの収入は離散確率変数として表現できて、

\[ X ( \mathrm{H} ) = 1, \; X ( \mathrm{T} ) = 0 \]

として定義した関数 \(X\) は離散確率変数となる。


例：単位区間上の乱数 （確率の項目の例の続き）

同様に、0以上1以下の実数値をランダムに取る乱数の例 \(\Omega = [0, 1]\) において「その乱数の値」そのものも確率変数として表現できて、

\[ X ( \omega ) = \omega \]

として定義した関数 \(X\) は連続確率変数となる。一方で、同じ \(( \Omega, \mathcal{F}, P )\) を用いても「乱数の値が0.5以上なら1円、それ以外なら0円」という賭けの収入のように

\[\begin{split} Y ( \omega ) = 1_{\omega \ge 0.5} = \begin{cases} 1, & \omega \ge 0.5 \\ 0, & \omega < 0.5 \end{cases} \end{split}\]

として定義した関数 \(Y\) は離散確率変数となる。


関連項目

  • 確率分布: 確率変数の実現値がそれぞれの値を取る確率を表現したもの

確率母関数#

  • 読み: かくりつぼかんすう

  • 英語での表現: probability generating function

  • Tags: 確率・統計

確率変数\(X\)が0以上の離散値を取るとき\(s^X\)の期待値\(G_X(s):=E[s^X]\)を確率母関数という。

\[ G_X(s)=E[s^X]=\sum_{x=0}^{\infty}s^xP(X=x) \]

確率母関数の1階微分と2階微分は次のようになる。

\[\begin{split} \begin{align*} G_X^{(1)}(s)&:=\frac{dG_X(s)}{ds}=E[Xs^{X-1}]\\ G_X^{(2)}(s)&:=\frac{d^2G_X(s)}{ds^2}=E[X(X-1)s^{X-2}] \end{align*} \end{split}\]

これを利用して確率変数\(X\)の期待値\(E[X]\)や分散\(V[X]\)を求めることができる。

\[\begin{split} \begin{align*} E[X]&=G_X^{(1)}(1)\\ V[X]&=E[X^2]-(E[X])^2\\ &=E[X(X-1)]+E[X]-(E[X])^2\\ &=G_X^{(2)}(1)+G_X^{(1)}(1)-(G_X^{(1)}(1))^2 \end{align*} \end{split}\]

確率密度関数#

  • 読み: かくりつみつどかんすう

  • 英語での表現: probability density function, PDF

  • Tags: 確率・統計

狭義には、連続確率変数の累積分布関数 \(F ( x )\) の導関数

\[\begin{split} \begin{align} f ( x ) & = \frac{d}{d x} F ( x ) \\ & = \frac{d}{d x} P ( X \le x ) \end{align} \end{split}\]

をその確率分布の確率密度関数と呼ぶ。ただし \(X: \Omega \to \mathbf{R}\) はこの分布に従う確率変数とする。確率密度関数は対応する連続確率分布を完全に特徴づける。

確率密度関数を利用することで、この連続確率分布に従う確率変数 \(X\) が \(a \le X \le b\) の範囲の値を取る確率を

\[ P ( a \le X \le b ) = \int_a^b f ( x ) d x \]

で表すことができる。任意の \(x \in \mathbf{R}\) についてこの \(X\) が一点 \(x\) を値に取る確率は \(P ( X = x ) = 0\) となることもここから容易に分かる。

より広義には、押し出し測度としての確率分布 \(P_X\) を何らかの標準測度 \(\mu\) でラドン・ニコディム微分して得た関数 \(f\) を確率密度関数と呼ぶ。この意味での確率密度関数は \(P_X\) が連続確率分布でない場合にも定義される。この場合、狭義の（元の意味での）確率密度関数はルベーグ測度 \(\lambda\) に絶対連続な \(P_X\) に対して \(\mu = \lambda\) としたものにあたり、確率関数は \(X\) の値域が \(\mathcal{X}\) 高々可算なときに \(\mu\) を \(\mathcal{X}\) 上の数え上げ測度としたものにあたる。

仮説検定#

  • 読み: かせつけんてい

  • 英語での表現: hypothesis testing

  • Tags: 確率・統計

母集団分布の母数に関する仮説を標本から検証する統計学的方法のひとつ。仮説が正しいと仮定した上で、それに従う母集団から、実際に観察された標本が抽出される確率を求め、その値により判断を行う。その確率が十分に有意水準より小さければ、その仮説を棄却する。仮説の設定、検定統計量の選択と算出、有意性の評価の3つの要素からなる。

ガンマ分布#

  • 読み: がんまぶんぷ

  • 英語での表現: gamma distribution

  • Tags: 確率・統計

単位時間中に平均\(\lambda\)回起こる事象が\(\alpha\)回起こるまでの時間が従う確率分布\(Ga(x;\alpha,\lambda)\)。

確率密度関数

\[f \left( x;\alpha,\lambda \right) =\frac{\lambda^{\alpha}}{\Gamma(\alpha)}x^{\alpha-1}\exp(-\lambda x)\]

ただし\(\Gamma(\alpha)\)はガンマ関数で

\[\Gamma(\alpha)=\int_0^{\infty}t^{\alpha-1}\exp(-t)dt\]

モーメント母関数

\[M_X(t)=\left(\frac{\lambda}{\lambda-t}\right)^{\alpha}\]

期待値

\[E[X]=\frac{\alpha}{\lambda}\]

分散

\[V[X]=\frac{\alpha}{\lambda^2}\]

再生性

互いに独立な\(X_i\sim Ga(x;\alpha_i,\lambda)\)について

\[X_1+X_2\sim Ga(x;\alpha_1+\alpha_2,\lambda)\]

ポアソン分布との関係性

\(\alpha\geq2\)かつ\(\alpha\in\mathbb{N}\)の場合、ガンマ分布とポアソン分布（ポアソン過程）は次の関係性にある。

\[\int_T^{\infty}\frac{\lambda^{\alpha}}{\Gamma(\alpha)}x^{\alpha-1}\exp(-\lambda x)dx=\sum_{x=0}^{\alpha-1}\frac{(\lambda T)^x}{x!}e^{-\lambda T}\]

これは単位時間中に平均\(\lambda\)回起こる事象の区間\([0,T]\)における発生回数が\(\alpha\)回未満である確率を示している。

き#

幾何分布#

  • 読み: きかぶんぷ

  • 英語での表現: geometric distribution

  • Tags: 確率・統計

無限に続く独立なベルヌーイ試行（成功確率\(p\)）において、初めて成功するまでの失敗回数が従う分布\(NB(x;1,p)\)。すなわち負の二項分布で\(r=1\)とした場合に相当する。

確率関数

\[ P(X=x)=p(1-p)^x\;\;\;(x=0,1,\ldots) \]

確率母関数

\[ G_X(s)=\frac{p}{1-(1-p)s} \]

期待値

\[ E[X]=\frac{1-p}{p} \]

分散

\[ V[X]=\frac{1-p}{p^2} \]

無記憶性

\[ P(X\geq x_1+x_2|X\geq x_1)=P(X\geq x_2) \]

期待値#

  • 読み: 期待値

  • 英語での表現: expected value

  • Tags: 確率・統計

確率変数 \(X: \Omega \to \mathbf{R}\) の取る値をそれぞれの値を取る確率で重み付き平均した値

\[ \mathrm{E} [ X ] = \int_\Omega X ( \omega ) d P ( \omega ) \]

をその確率変数の期待値という。

特に \(X\) が離散確率分布に従う変数で確率関数 \(f_\mathrm{m} ( x )\) が既知の場合は

\[ \mathrm{E} [ X ] = \sum_{x \in \mathcal{X}} x f_\mathrm{m} ( x ) \]

と表せる。ただし \(\mathcal{X}\) は \(X\) の値域とする（この場合は高々可算な集合となる）。

また、 \(X\) が連続確率分布に従う変数で確率密度関数 \(f ( x )\) が既知の場合は

\[ \mathrm{E} [ X ] = \int_\mathbf{R} x f ( x ) d x \]

と表せる。

帰無仮説#

  • 読み: きむかせつ

  • 英語での表現: null hypothesis

  • Tags: 確率・統計

仮説検定を行うとき、最初に立てる仮説のこと。この仮説をもとに仮説検定を行い結論を導く。帰無仮説は棄却されることを前提に立てられることが多く、この仮説が棄却されると対立仮説が採択される。一般的に\(H_0\)と表記される。

キュムラント#

  • 読み: きゅむらんと

  • 英語での表現: cumulant

  • Tags: 確率・統計

確率変数 \(X\) の キュムラント母関数 (cumulant generating function)

\[ K (t) = \log E [ e^{t X} ] \]

を0の周りで冪級数展開した表現

\[ K ( t ) = \sum_{n = 1}^\infty \kappa_n \frac{t^n}{n!} = \kappa_1 \frac{t}{1!} + \kappa_2 \frac{t^2}{2!} + \cdots \]

に現れる係数 \(\kappa_n\) を \(X\) の \(n\) 次のキュムラント ( \(n\)-th cumulant) と呼ぶ。

4次までのキュムラントは \(X\) のモーメントを用いて

  • \(\kappa_1 = \mu_1^{(0)}\) (平均)

  • \(\kappa_2 = \mu_2\) (分散)

  • \(\kappa_3 = \mu_3\) (標準化すれば歪度に対応)

  • \(\kappa_4 = \mu_4 - 3 \mu_2^2\) (標準化すれば過剰尖度に対応)

のように表せる。ただし原モーメントを \(\mu_n^{(0)}\) 、中心化モーメントを \(\mu_n\) と置いた。

また、正規分布においては3次以上のキュムラントがすべて0となる。

強化学習#

  • 読み: きょうかがくしゅう

  • 英語での表現: reinforcement learning, RL

  • Tags: 機械学習

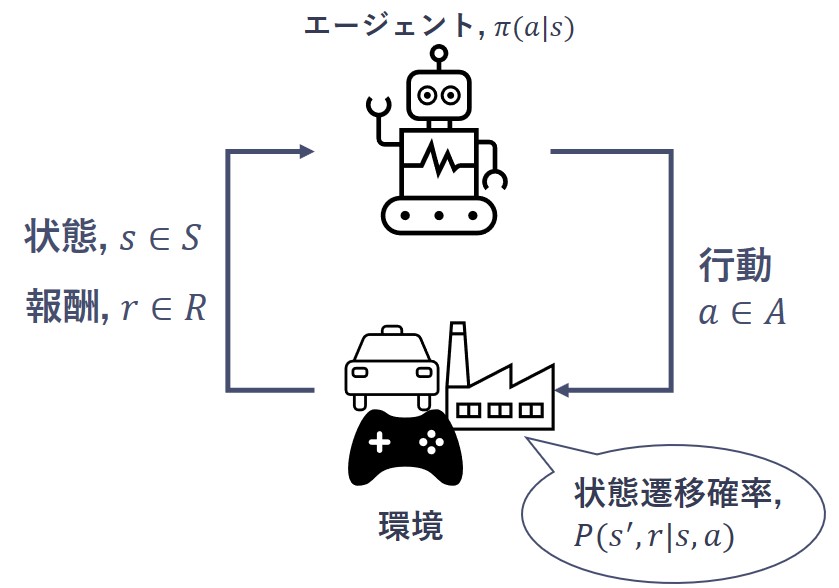
システム自身が、試行錯誤の中で最適な方策（=制御手法、行動基準、ルール）を求める機械学習手法。行動主体であるエージェントと制御対象の環境 により定式化される。エージェントは方策\(\pi(a|s)\) で表される行動基準に基づき, 環境へ行動を送出し, その結果として次の状態\(s'\) と行動の評価基準である報酬\(r'\) を受け取る。エージェントは将来にわたって得られる報酬を最大化するように方策を逐次更新する。このようなエージェントと環境の相互作用のなかで、データを反復的に収集しながら最適方策を探索する。

初めからすべてのデータが与えられているわけではなく、探索を通して新たに得た知識を活用しながら最適の行動を選択できるよう学習するという点で、教師あり学習/教師なし学習とは分野分けされる。

また、制御工学の分野における最適制御と関係が深い。

rl

強定常性#

  • 読み: きょうていじょうせい

  • 英語での表現: strict stationarity

  • Tags: 確率・統計

強定常性は、定常性のうち、確率過程の有限次元分布が時間シフトに関して不変であること。つまり、任意の時刻\(t\) と\(k\) に対して、\((y_t, y_{t+1}, \cdots, y_{t+k})\) の同時分布が同一となる場合、強定常性を満たす。
強定常性を満たすデータはあまり多くは存在しないが、代表例として各時点のデータが互いに独立かつ同一の分布に従うiid系列が知られている。

関連項目

共分散#

  • 読み: きょうぶんさん

  • 英語での表現: covariance

  • Tags: 確率・統計

確率分布やデータの特徴を表す指標の一つで、平均を中心として複数の確率変数やカラムの値がどのようにばらつくかの傾向を示すもの。確率変数 \(X, Y\) の平均をそれぞれ \(\mu_X, \mu_Y\) としたとき、 \(X, Y\) の共分散を

\[ \sigma_{X Y} = \mathrm{Cov} ( X , Y ) = \mathrm{E} [ ( X - \mu_X ) ( Y - \mu_Y ) ] \]

で定める。特に、自分自身との共分散 \(\mathrm{Cov} ( X , Y )\) は分散 \(\mathrm{V} [ X ]\) に一致する。データ \(\{ ( X_1, Y_1 ), \ldots, ( X_n, Y_n ) \}\) について、 \(\{ X_i \}, \{ Y_i \}\) の標本平均をそれぞれ \(\bar{X}, \bar{Y}\) としたとき、このデータの標本共分散 (sample covariance) は

\[ \frac{1}{n} \sum_{i=1}^n ( X_i - \bar{X} ) ( Y_i - \bar{Y} ) \]

を指すこともあれば、 \(n\) の代わりに \(n - 1\) で除した

\[ \frac{1}{n - 1} \sum_{i=1}^n ( X_i - \bar{X} ) ( Y_i - \bar{Y} ) \]

を指すこともある。 \(( X_i, Y_i )\) の組が独立同分布のとき、後者の標本共分散は元の分布の共分散の不偏推定量になっており、これゆえ特に不偏（標本）共分散とも呼ばれる。

共役事前分布#

  • 読み: きょうやくじぜんぶんぷ

  • 英語での表現: conjugate prior distribution

  • Tags: 確率・統計

ベイズ統計において、データ \(X\) を観測した後の興味のある量 \(\theta\) の事後分布 \(p ( \theta | X )\) が対応する事前分布 \(p ( \theta )\) と同じ分布族に属する場合、この事前分布 \(p ( \theta )\) を尤度関数 \(p ( X | \theta )\) に対する共役事前分布と呼ぶ。尤度関数が指数型分布族であれば共役事前分布を持ち、共役事前分布を用いれば対応する事後分布を陽に求めることができることから計算上の便利のためしばしば利用される。

例えば試行回数 \(n\) を固定した二項分布 \(k \sim \mathrm{B} ( n, p )\) の尤度関数について、成功確率 \(p\) の共役事前分布はベータ分布 \(\mathrm{Be} ( \alpha, \beta )\) であり、対応する事後分布は \(\mathrm{Be} ( \alpha + k, \beta + n - k )\) となる。

く#

クロスバリデーション#

交差検証に同じ

け#

決定係数#

  • 読み: けっていけいすう

  • 英語での表現: coefficient of determination

  • Tags: 確率・統計

説明変数が目的変数をどの程度説明できるかを表す値で、標本値から求めたモデル（回帰方程式）の当てはまりの良さの尺度。\(R^2\)と表記される。機械学習の評価指標のとして、主に回帰問題で使用される。寄与率と呼ばれることもある。

決定係数\(R^2\)はさまざまなバリエーションがあり、明確に合意された定義はない。しかし、一般的には次の式を定義とすることが多い。ここで、サンプルごとの予測値と真値を\(\hat{y}_i\)と\(y_i\)とし、\(\bar{y}\)は真値の平均値である。

\[ R^2=1-\frac{\sum_{i=1}^n(y_i-\hat{y}_i)^2}{\sum_{i=1}^n(y_i-\bar{y})^2} \]

一方で、説明変数の数が増えると決定係数は過大になる傾向がある。そのため、説明変数の総数\(p\)に応じて決定係数が小さくなるように補正した、次の自由度調整済み決定係数\(R^{\prime 2}\)もよく用いられる。

\[ R^{\prime 2}=1-\frac{\frac{1}{n-p-1}\sum_{i=1}^n(y_i-\hat{y}_i)^2}{\frac{1}{n-1}\sum_{i=1}^n(y_i-\bar{y})^2} \]

検定統計量#

  • 読み: けんていとうけいりょう

  • 英語での表現: test statistic

  • Tags: 確率・統計

仮説検定において、帰無仮説が正しいと仮定したときに、観測した事象をその検定に合わせて要約した値。仮説検定では、データから算出された検定統計量より極端な値をとる確率を、有意水準と比較することで帰無仮説を棄却するかどうかを判断する。

こ#

交差検証#

  • 読み: こうさけんしょう

  • 英語での表現: cross validation

  • Tags: 機械学習・統計

統計学や機械学習において、モデルの汎化性能を評価するための手法。 モデルの推定に使用できるデータを訓練用/検証用に分割し、訓練データのみで学習した後、検証データでその推定精度を図る（ホールドアウト法）。しかし、単純な検証では、分割の仕方によってデータの分布が偏る、モデル設計を繰り返した結果検証データに対して過剰適合（オーバーフィッティング）する、データ数が少ない場合十分な検証ができないといった問題がある。

最も基本的な交差検証であるk-分割交差検証 (k-fold クロスバリデーション)　では、全データをk個に分割、そのうちの1つを検証データ、残りk-1個で学習し評価するプロセスを、全パターンについて実施する。それぞれのパターンでの評価指標の平均値がモデルの汎化性能として採用される。

関連項目

目次