定常性の確認#

時系列データの解析において、データの有する時不変な性質の確認はその後の解析・モデリングの指針を検討する上での重要な指針となります。定常性（stationarity）とはこのうちデータの従う確率過程に関する性質で、大きく分けて強定常性（strict stationarity）と弱定常性（weak stationarity）の2つの概念があります。それぞれ、大まかには

強定常性：確率過程の有限次元分布が時間シフトに関して不変であること
弱定常性：確率過程の平均・自己共分散（・相互共分散）が有限で、時間シフトに関して不変であること

という意味になります。ここでいう有限次元分布、平均・自己共分散（・相互共分散）などはすべて無条件の（即ち、条件付けられていない）ものであることに注意してください。

時系列データの従う確率過程に定常性があるということは、その確率過程に関してある時刻のデータから推測した情報を異なる時刻での推測に利用することに意味があるということです。このため、時系列解析で用いられる統計的モデリングには、特に予測の観点からデータの定常性を（暗に）要請しているものが多くあります。特に経済・金融系の時系列解析では、系列データを定常的な成分と非定常的な成分に分解した上で、あるいは差分系列を取るなどしてデータを定常系列に変換した上で、その定常系列に対してモデリングを実施することがしばしば行われます。

また、DCSデータなどの製造工程のデータを時系列データとして解析する際には、逆に訓練データが定常性を有しているように見える場合に注意が必要となることがあります。例えば、製造工程の中でフィードバック制御が行われている場合の設定値（SV）の変化、データのサンプリング周期と比較して遥かに長大な周期の季節成分の存在、同一の製造工程で複数の製品を生産している際の製品の切り替えなどが想定される場合がこれに該当します。このような場合、モデルの汎化性能をいずれの場合も、データに関するドメイン知識を適切に活用してデータの適切な変換を行うか、モデルが予測に責任を持てる入力データの領域やデータ外の要因について適切に制限することが望ましくなります。

本項では、確率過程の定常性とその代表的な確認方法について簡単に説明します。

準備#

import warnings

warnings.filterwarnings("ignore")

import datetime as dt

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import statsmodels.tsa.api as tsa

%matplotlib inline
# matplotlibでは日本語にデフォルトで対応していないので、日本語対応フォントを読み込む
plt.rcParams["font.family"] = "BIZ UDGothic"  # Windows
# plt.rcParams['font.family'] = 'Hiragino Maru Gothic Pro' # Mac

# その他使えるフォント一覧は以下のコードで取得できます。
# import matplotlib.font_manager
# [f.name for f in matplotlib.font_manager.fontManager.ttflist]

np.random.seed(42)

FILE_PATH = "../data/2020413_raw.csv"
df = pd.read_csv(FILE_PATH, index_col=0, parse_dates=True, encoding="shift-jis")

df.head()

	気化器圧力_PV	気化器圧力_SV	気化器圧力_MV	気化器圧力_MODE	気化器液面レベル_PV	気化器液面レベル_SV	気化器液面レベル_MV	気化器液面レベル_MODE	気化器温度_PV	気化器ヒータ出口温度_PV	...	反応器流入組成（H2O）_PV	反応器流入組成（HAc）_PV	セパレータ蒸気排出量_MV (Fixed)	セパレータ蒸気排出量_MODE (Fixed)	アブソーバスクラブ流量_MV (Fixed)	アブソーバスクラブ流量_MODE (Fixed)	アブソーバ還流流量_MV (Fixed)	アブソーバ還流流量_MODE (Fixed)	気化器液体流入量_MV (Fixed)	気化器液体流入量_MODE (Fixed)
2020-04-13 00:00:00	127.983294	127.883920	18.728267	AUT	0.700204	0.7	21876.987772	AUT	120.15955841553482	151.274003	...	0.008524	0.109444	16.1026	AUT	15.1198	AUT	0.766	MAN	2.1924	AUT
2020-04-13 00:00:01	128.262272	127.807691	18.728267	AUT	0.700865	0.7	21876.987772	AUT	120.07257486304935	151.218620	...	0.008512	0.109441	16.1026	AUT	15.1198	MAN	0.766	MAN	2.1924	AUT
2020-04-13 00:00:02	127.899077	127.991074	19.079324	AUT	0.699740	0.7	21918.359526	AUT	120.30532712904707	151.201067	...	0.008541	0.109871	16.1026	AUT	15.1198	AUT	0.756	MAN	2.1924	AUT
2020-04-13 00:00:03	127.622218	127.990697	18.772228	AUT	0.699970	0.7	21892.166478	AUT	120.21948819246609	151.220816	...	0.008573	0.109775	16.1026	AUT	15.1198	AUT	0.746	MAN	2.1924	AUT
2020-04-13 00:00:04	127.577243	127.903788	18.605173	AUT	0.700939	0.7	21885.688813	AUT	120.30226736316207	151.165624	...	0.008547	0.109868	16.1026	AUT	15.1198	AUT	0.766	MAN	2.1924	AUT

5 rows × 117 columns

一変量時系列の定常性#

この節では、一変量時系列に対する定常性の定義を示し、定常性の判断に利用できる幾つかの方法について簡単に述べます。

強定常性#

連続時間の実数値確率過程 \(\{ X_t \}_{t \in \mathbf{R}}\) が強定常であるとは

\[\begin{split} \begin{array}{l} \forall n \in \mathbf{N} . \forall \tau, t_1, \ldots, t_n \in \mathbf{R} . \\ P ( X_{t_1}, \ldots, X_{t_n} ) \overset{d}{=} P ( X_{\tau + t_1}, \ldots, X_{\tau + t_n} ) \end{array} \end{split}\]

をみたすことを言います。どのような時刻の組を選んでも、それを時間 \(\tau\) だけシフトさせたときに同時分布が変化しないという条件です。あくまで無条件の同時分布であり、条件付きの分布に対する言及ではないことに注意してください。

弱定常性#

連続時間の実数値確率過程 \(\{ X_t \}_{t \in \mathbf{R}}\) に対し、その平均関数と自己共分散関数をそれぞれ

\(m_X ( t ) = \mathrm{E} [ X_t ]\)
\(K_{XX} ( t_1, t_2 ) = \mathrm{E} [ ( X_{t_1} - m_X ( t_1 ) ) ( X_{t_2} - m_X ( t_2 ) ) ]\)

で定めます。このとき、 \(\{ X_t \}_{t \in \mathbf{R}}\) が弱定常であるとは

\(\forall \tau, t \in \mathbf{R} . m_X ( t ) = m_X ( \tau + t)\)
\(\forall t_1, t_2 \in \mathbf{R} . K_{XX} ( t_1, t_2 ) = K_{XX} ( t_1 - t_2, 0 )\)
\(\forall t \in \mathbf{R} . \mathrm{E} [ | X_t | ^2 ] < 0\)

の3条件を満たすことを言います。平均が時間シフトに対して不変であることは1つめの条件に、自己共分散が時間シフトに対して不変であること（即ち、2時刻間のラグのみに依存すること）は2つめの条件に対応します。こちらも条件付きの期待値や自己共分散に対する言及ではないことに注意してください。

時系列の描画による確認#

定常性を確認するための最も簡易な方法は、単純にその時系列を時間領域でプロットしてみることです。幾つかの非定常過程には特徴があるため、時間領域でのプロットを見ることでそうした非定常性を疑うことができます。

代表的な定常・非定常過程のプロット#

例えば定常過程の代表例であるホワイトノイズや、係数を適切に設定した自己回帰過程 AR(1) のサンプルパスをプロットしてみたものは次のようになります。

# ホワイトノイズの生成
xx_wn = np.random.normal(size=(1000,))

# AR(1)の生成
x_prev = 0.0
xx_ar = np.zeros(shape=(1000,))

for i in range(1000):
    xx_ar[i] = 0.5 * x_prev + np.random.normal()
    x_prev = xx_ar[i]


# 描画
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 5))

ax1.plot(xx_wn)
ax1.set_title("N(0, 1) i.i.d.")
ax1.grid()

ax2.plot(xx_ar)
ax2.set_title("AR(1) with phi=0.5")
ax2.grid()

plt.show()

../_images/eba2b3a3ba6ce8ee0f590113241e6ee5160adee2ffc946ef0a247bdf7e020b52.png

定常過程では各時刻の（条件づけられていない）平均・分散が時間シフトに対して不変なので、そのサンプルパスを描画すると長期的には横一直線の周りにある程度の幅で振動するノイズのように見えます。定常性は条件付きの平均・分散に関する性質ではないので、短期的にはある程度の偏りが発生しうることに注意してください。

一方、ホワイトノイズに決定的なトレンドを加えた確率過程や、ホワイトノイズが時間的に拡大されていくような確率過程は定常過程ではありません。

xx_ln = np.arange(1000)
xx_lt = 0.01 * xx_ln + np.random.normal(size=(1000,))
xx_av = 0.01 * xx_ln * np.random.normal(size=(1000,))

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 5))

ax1.plot(xx_lt)
ax1.set_title("White Noise with Linear Trend")
ax1.grid()

ax2.plot(xx_av)
ax2.set_title("White Noise Amplified Linearly")
ax2.grid()

plt.show()

../_images/40c69f35deda675a5e4e96c6f48e21ba4986c689560c42a668c041d3afaac917.png

また、ランダムウォークのように確率的なトレンドを含む確率過程も一般には非定常過程になります。

x_prev = 0.0
xx_rw = np.zeros(shape=(1000,))

for i in range(1000):
    xx_rw[i] = x_prev + np.random.normal()
    x_prev = xx_rw[i]


fig, ax = plt.subplots(1, 1, figsize=(7, 5))

ax.plot(xx_rw)
ax.set_title("Random Walk")
ax.grid()

plt.show()

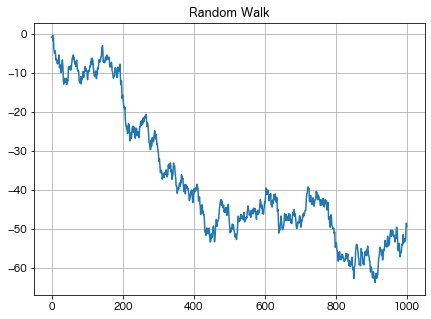
../_images/a3dd6f71ddf97f963ece6bf6d82fd56252bc24a2bcf4135f574e5c9318846df6.png

DCSデータのプロットと定常性#

上記の主要な定常・非定常過程のプロットの特徴を踏まえた上で、実際にDCSデータのプロットを見てみましょう。

colname_pv = "反応器流入組成（O2）_PV"

fig, ax = plt.subplots(1, 1, figsize=(7, 5))

df[colname_pv].plot(ax=ax)
ax.set_title(colname_pv)
ax.grid()

plt.show()

../_images/14bfda6293e3e103b6812770c8c854a7f12e3caa2c944c67a862d628ae95ce29.png

上記の図は適当なセンサーの測定値（PV）を時間領域でプロットしたものです。データの平均は時刻によって変化しているように見えます。この時系列の場合、少なくとも非定常性を疑ってみる必要がありそうです。

一般に、DCSデータで測定値に対応する系列については制御の対象となっていて対応する設定値（SV）が存在すれば本質的には非定常だと思って問題ありません。実際、上記の測定値にもデータの中に対応する設定値が存在します。設定値の系列と、設定値から測定値を引いた制御偏差（DV）の系列をプロットしてみると次のようになります。

colname_sv = "反応器流入組成（O2）_SV"
sr_dv = df[colname_sv] - df[colname_pv]  # 制御偏差（DV）の系列を計算

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 5))

# 設定値（SV）の系列をプロット
df[colname_sv].plot(ax=ax1)
ax1.set_title(colname_sv)
ax1.grid()

# 制御偏差（DV）の系列をプロット
sr_dv.plot(ax=ax2)
ax2.set_title(f"{colname_sv} - {colname_pv}")
ax2.grid()

plt.show()

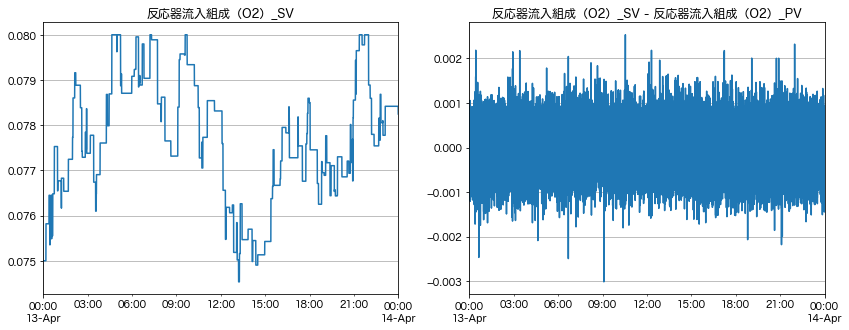
../_images/ad7628a7b8c98f54c9f3db45181f48ddf5077e812c5d697a75aa7df17de3f801.png

制御偏差の系列は一見して定常過程らしく見えなくもありません。

ヒストグラムの描画による確認#

定常過程では、各時刻におけるデータの分布が時刻に依存しません。従って、時刻によってデータの経験分布が大きく異なるようであれば非定常性を疑う契機になります。本節では上記DCSデータの測定値と制御偏差について、適当な時刻で分割した前後のヒストグラムを比較することで定常性に関する示唆を求めてみます。

threshold = dt.datetime(2020, 4, 13, 12)  # 2020/4/13, 12:00を境に系列を分割
index_fh = df.index < threshold
index_lh = df.index >= threshold

xlim = (df[colname_pv].min(), df[colname_pv].max())
bins = np.linspace(*xlim, 21)  # 比較のためにヒストグラムのbinsを揃える

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 5))

# 2020/4/13, 12:00以前のヒストグラム
df[colname_pv][index_fh].hist(ax=ax1, bins=bins)
ax1.set_xlim(xlim)
ax1.set_title(f"{colname_pv}, 〜{threshold}")

# 2020/4/13, 12:00以降のヒストグラム
df[colname_pv][index_lh].hist(ax=ax2, bins=bins)
ax2.set_xlim(xlim)
ax2.set_title(f"{colname_pv}, {threshold}〜")

plt.show()

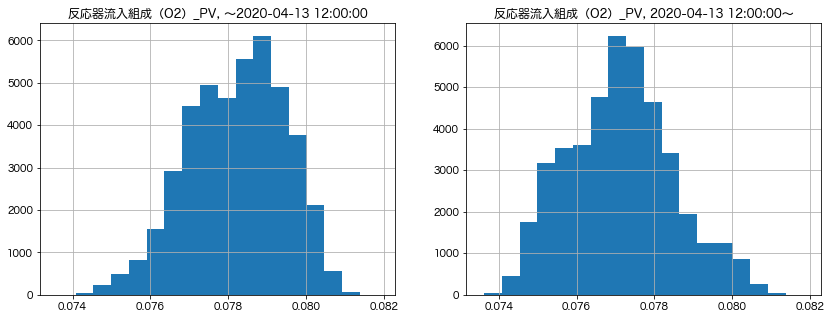
../_images/4bbba4474a1c555da0709448da1de193d209800128f2236eb589694a039e6e89.png

測定値のヒストグラムは4/13の12:00を境に峰の位置などが異なり、その系列には非定常性のあることが推測されます。

plt.figure(figsize=(14, 5))
xlim = (sr_dv.min(), sr_dv.max())
bins = np.linspace(*xlim, 21)  # 比較のためにヒストグラムのbinsを揃える

# 2020/4/13, 12:00以前のヒストグラム
plt.subplot(1, 2, 1)
plt.xlim(xlim)
sr_dv[index_fh].hist(bins=bins)
plt.title(f"{colname_sv} - {colname_pv},\n〜{threshold}")

# 2020/4/13, 12:00以降のヒストグラム
plt.subplot(1, 2, 2)
plt.xlim(xlim)
sr_dv[index_lh].hist(bins=bins)
plt.title(f"{colname_sv} - {colname_pv},\n{threshold}〜")

plt.show()

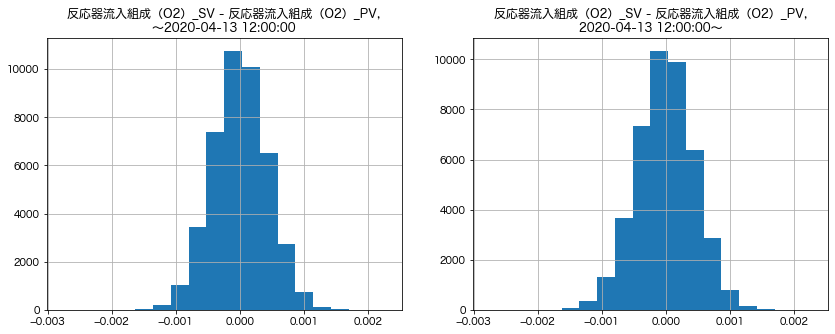
../_images/0d6cafe5e1ed26ad9d3de19ab0f96e2542e7703b734b3a03447ce3eeddec3ba6.png

一方、制御偏差のヒストグラムについては4/13の12:00の前後で大きな違いがなく、この比較のみでは制御偏差の系列について非定常性を強く疑うには至りません。

統計的検定による確認#

定常性を確認するための統計的検定としてはさまざまなものが考案されていますが、ここでは拡張Dickey-Fuller検定を利用するものについて簡単に触れます。

拡張Dickey-Fuller検定による定常性の確認#

拡張Dickey-Fuller検定（ADF検定）は確率過程に自己回帰モデルを仮定する場合の代表的な単位根検定ですが、自己回帰モデルで特性方程式に絶対値の1より大きい根を持つようなものはサンプルパスが指数的に発散してしまうため、実用的には（自己回帰モデルを仮定する場合の）確率過程の定常性の検定として利用することができます。本節ではADF検定を利用した定常性の確認の手続きについてのみ述べます。ADF検定の詳細は単位根の項を参照してください。

上記の測定値の系列に（設定値の存在を忘れて）有意水準5%のADF検定を実施した結果は次のようになります。

adf_rlt_pv = tsa.adfuller(df[colname_pv].values)

print(f"ADF statistics: {adf_rlt_pv[0]}")
print(f"# of lags used: {adf_rlt_pv[2]}")
print(f"Critical values: {adf_rlt_pv[4]}")

ADF statistics: -2.6856932356155223
# of lags used: 16
Critical values: {'1%': -3.430425702610773, '5%': -2.8615734593098154, '10%': -2.5667878092299223}

検定統計量は5%-棄却域に入らず、帰無仮説（単位根の存在）は棄却されません。即ち、有意水準5%では測定値の系列に単位根が存在する（ゆえに非定常である）と考えられることになります。

adf_rlt_dv = tsa.adfuller(sr_dv.values)

print(f"ADF statistics: {adf_rlt_dv[0]}")
print(f"# of lags used: {adf_rlt_dv[2]}")
print(f"Critical values: {adf_rlt_dv[4]}")

ADF statistics: -11.450070158595876
# of lags used: 26
Critical values: {'1%': -3.4304257113755474, '5%': -2.8615734631836522, '10%': -2.5667878112918396}

検定統計量は5%-棄却域に入り、帰無仮説（単位根の存在）は棄却されます。即ち、有意水準5%では制御残差の系列に単位根が存在する（ゆえに非定常である）とは考えないことになります。

局所的な定常性について#

冒頭でも述べた通り、DCSデータではむしろ訓練データが定常性を有しているように見える場合に注意が必要です。例えば上記の測定値の系列は一見して非定常ですが、もし訓練データとして与えられているのがごく一部だけであればどう見えるでしょう。

stat_bound_0 = dt.datetime(2020, 4, 13, 18)  # 2020/4/13, 18:00を境界に指定
stat_bound_1 = dt.datetime(2020, 4, 13, 21)  # 2020/4/13, 21:00を境界に指定

stat_duration = (stat_bound_0 < df.index) & (df.index < stat_bound_1)
sr_pv_stat = df[colname_pv][stat_duration]
sr_sv_stat = df[colname_sv][stat_duration]

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 5))

# 測定値（PV）の系列をプロット
sr_pv_stat.plot(ax=ax1)
ax1.set_title(f"{colname_pv},\n{stat_bound_0}〜{stat_bound_1}")
ax1.grid()

# 設定値（SV）の系列をプロット
sr_sv_stat.plot(ax=ax2)
ax2.set_title(f"{colname_sv},\n{stat_bound_0}〜{stat_bound_1}")
ax2.grid()

plt.show()

../_images/2dc569208841d5e3ea80af52ed89006e6fb9b88236ba86e01c8f8337dcc78a8d.png

この期間の測定値の系列は、一見して定常であるかどうかの判断が困難です。

有意水準5%でADF検定を実施してみるとどうなるでしょうか。

adf_rlt_pv_stat = tsa.adfuller(sr_pv_stat.values)

print(f"ADF statistics: {adf_rlt_pv_stat[0]}")
print(f"# of lags used: {adf_rlt_pv_stat[2]}")
print(f"Critical values: {adf_rlt_pv_stat[4]}")

ADF statistics: -3.3201764954054993
# of lags used: 12
Critical values: {'1%': -3.4309564210049537, '5%': -2.8618080041618827, '10%': -2.5669126534795277}

検定統計量は5%-棄却域に入り、帰無仮説（単位根の存在）は棄却されます。即ち、有意水準5%では測定値の系列に単位根が存在する（ゆえに非定常である）とは考えないことになります。

もしこの期間の測定値のみが訓練データとして与えられていたとすると、グラフや検定統計量を注意深く眺めない限り測定値の系列が非定常である可能性には思い至らないかもしれません。しかし、その前後の時刻の情報を知っていれば、少なくとも対応する設定値や影響を与える他変数の存在を疑い、それらの影響を除外した上で改めて系列の定常性を確認する必要がありそうなことは一見して明らかです。DCSデータなどの製造工程のデータを解析する際は、データの定常性に関する判断は慎重に行う必要があります。

多変量時系列の定常性#

多変量時系列の定常性について、ここでは結合定常性（joint stationarity）、特に結合強定常性（joint strict stationarity）と結合弱定常性（joint weak stationarity）について簡単に説明します。結合定常性は自己回帰分布ラグモデル（いわゆる線形回帰）などで時系列予測を行う際に要請される仮定の一部を構成します。

結合強定常性#

連続時間の実数値確率過程 \(\{ X_t \}_{t \in \mathbf{R}}, \{ Y_t \}_{t \in \mathbf{R}}\) が結合強定常であるとは

\[\begin{split} \begin{array}{l} \forall m, n \in \mathbf{N} . \forall \tau, t_1, \ldots, t_{m}, t_{m + 1}, \ldots, t_{m + n} \in \mathbf{R} . \\ P ( X_{t_1}, \ldots, X_{t_m}, Y_{t_{m + 1}}, \ldots, Y_{t_{m + n}} ) \overset{d}{=} P ( X_{\tau + t_1}, \ldots, X_{\tau + t_m}, Y_{\tau + t_{m + 1}}, \ldots, Y_{\tau + t_{m + n}} ) \end{array} \end{split}\]

をみたすことを言います。一変量の場合と同様、任意の有限次元分布が時間シフトに対して不変であることを指します。

結合弱定常性#

連続時間の実数値確率過程 \(\{ X_t \}_{t \in \mathbf{R}}, \{ Y_t \}_{t \in \mathbf{R}}\) に対し、その相互共分散関数を

\(K_{XY} ( t_1, t_2 ) = \mathrm{E} [ ( X_{t_1} - m_X ( t_1 ) ) ( Y_{t_2} - m_Y ( t_2 ) ) ]\)

で定めます。このとき、 \(\{ X_t \}_{t \in \mathbf{R}}\) が結合弱定常であるとは

\(\forall \tau, t \in \mathbf{R} . m_X ( t ) = m_X ( \tau + t )\)
\(\forall \tau, t \in \mathbf{R} . m_Y ( t ) = m_Y ( \tau + t )\)
\(\forall t_1, t_2 \in \mathbf{R} . K_{XX} ( t_1, t_2 ) = K_{XX} ( t_1 - t_2, 0 )\)
\(\forall t_1, t_2 \in \mathbf{R} . K_{YY} ( t_1, t_2 ) = K_{YY} ( t_1 - t_2, 0 )\)
\(\forall t_1, t_2 \in \mathbf{R} . K_{XY} ( t_1, t_2 ) = K_{XY} ( t_1 - t_2, 0 )\)
\(\forall t \in \mathbf{R} . \mathrm{E} [ | X_t | ^2 ] < 0\)
\(\forall t \in \mathbf{R} . \mathrm{E} [ | Y_t | ^2 ] < 0\)

の全条件を満たすことを言います。即ち、各系列が弱定常で相互共分散が時間シフトに対して不変であること（即ち、2時刻間のラグにのみ依存すること）を言います。

小括#

本項では、確率過程の定常性とその代表的な確認方法について簡単に説明しました。単位根や共和分に関する項と併せて、時系列データが持つ性質についての理解を深めるのに役立ててください。

参考文献#

Stock, J. H. and Watson M. W. (2007). Introduction to Econometrics. Pearson Education. (宮尾龍蔵 (訳, 2016). 入門計量経済学. 共立出版.)

定常性の確認

目次