次元削減#

※機械学習の文脈の「次元削減」や「次元圧縮」は日本語に多少ブレがあります。

ここでは高次元空間上のデータについて、

列の要素に変更は加えず、個々の列（軸）を削減することで低次元化を達成する手法を「次元削減」（VIFなど）
列の要素の変換も伴うような、何らかの写像によって低次元空間に射影する手法を「次元圧縮」（PCAなど）

と呼ぶことにします。

本項では「次元削減」について、

変動が微少な列の除外
多重共線性（後述）の回避

の２つの観点からまとめます。

多重共線性とは#

重回帰分析を行っている際、説明変数を増やすほど決定係数が高くなりやすいため、ついついよりたくさんの説明変数を入れてしまいがちです。
しかし、その際に気をつけなければならないことがあります。それが多重共線性です。
多重共線性とは、説明変数間で相関係数が高いときに、それが原因で発生する現象です。英語で multicollinearity と言われるため、略して「マルチコ」とも呼ばれます。

多重共線性が問題となる理由

分析結果における係数の標準誤差が大きくなる
\(t\) - 値が小さくなる
決定係数が大きな値となる
回帰係数の符号が本来なるべきものとは逆の符号となる

などがあり、いずれも、正しく推定できなくなるような悪影響をもたらします。

多重共線性の対応方法

このような多重共線性に直面してしまった場合、最も一般的な解消法は、「相関関係が高いと考えられる説明変数を外すこと」です。
たとえば、ある3階建ての建物の一日の「電力消費量」を目的変数とした分析を行うケースを考えてみます。ある日の電力消費量に関係しそうな要素として、その日の1〜３階各階の最高気温と、降水量を考慮することにします。ここで、例えば、２階と３階の最高気温は日によらず同じような値をとり、相関関係が高かったとしましょう。この状態で２階と３階の最高気温を説明変数に含めて重回帰分析を行うと、多重共線性の問題が発生やすくなります。

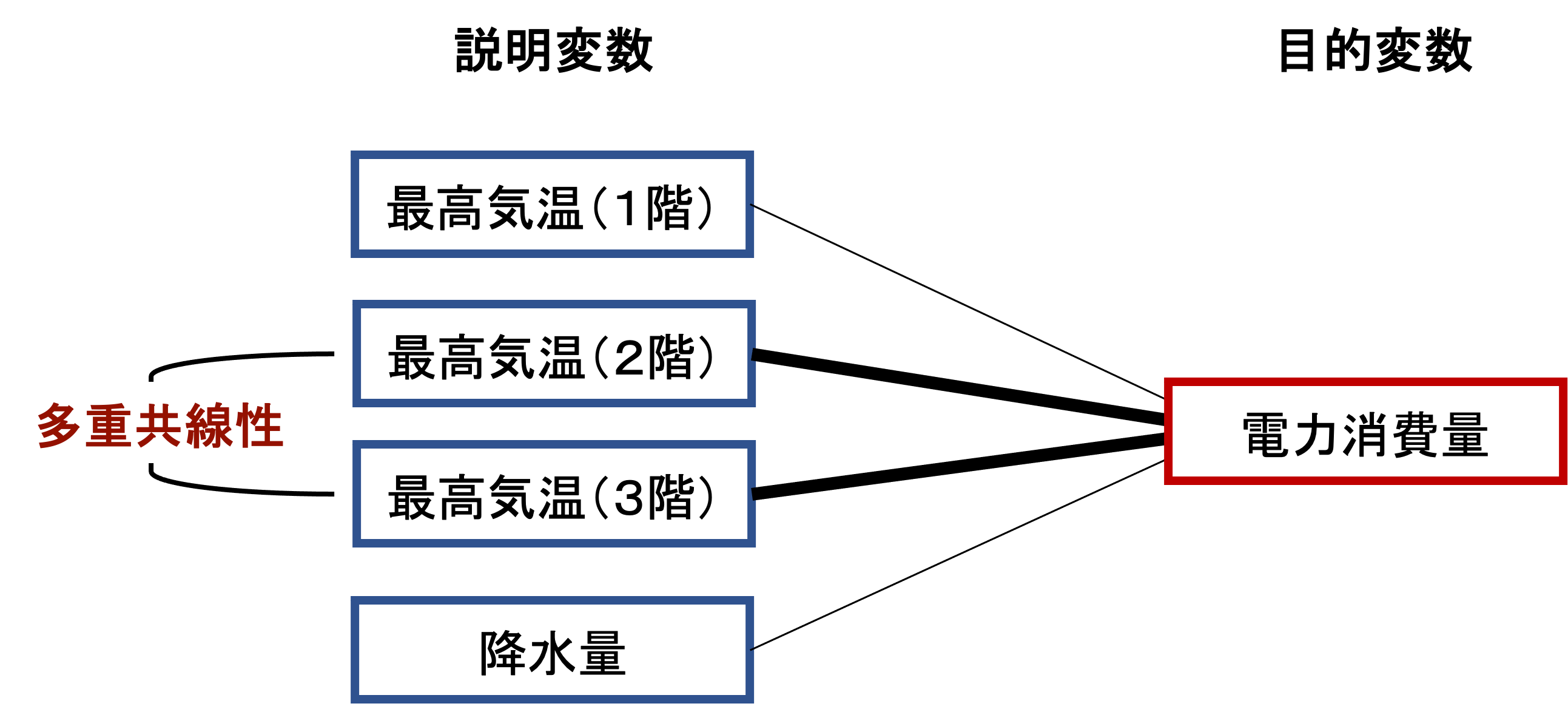
multico-s

このような場合は、どちらか一方を外して再度分析することで、多重共線性を解消することができます。

この例は、相関関係が高そうな説明変数が2つあるケースを考えましたが、これが3つ以上になった場合はどのように対処するのが望ましいでしょうか？
この場合も、基本的には1つに絞って分析することが一般的です。
しかし、説明変数の数をあまり減らしたくない場合（もともと説明変数の候補が非常に少ない場合など）は、ひとつずつ除外した分析を繰り返し、解消される組み合わせを探すという進め方もできます。
相関関係が高そうな説明変数が3つ以上ある場合、1つに絞らなくても多重共線性が解消される場合もあるからです。
また、相関している説明変数を除外する場合、どの変数を外すべきか悩むこともあります。
その場合は、主観的な判断で残しておきたい方の変数を残して問題ありません。
どちらを外しても問題ない場合は、それぞれ片方ずつ外して分析し、その結果を比較して\(t\)-値（偏回帰係数の値が意味を持つかどうかに関する指標で重回帰分析の項にて触れる予定）が高い方を残すという判断が良いと思います。

データの読み込み#

import warnings

warnings.filterwarnings("ignore")

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

# matplotlibでは日本語にデフォルトで対応していないので、日本語対応フォントを読み込む
plt.rcParams["font.family"] = "BIZ UDGothic"  # Windows
# plt.rcParams['font.family'] = 'Hiragino Maru Gothic Pro' # Mac

# 使えるフォント一覧は以下のコードで取得できます。
# import matplotlib.font_manager
# [f.name for f in matplotlib.font_manager.fontManager.ttflist]

pd.set_option("display.max_rows", 10)
pd.set_option("display.max_columns", 10)

fpath = "../data/2020413.csv"
df = pd.read_csv(fpath, index_col=0, parse_dates=True, encoding="shift-jis")

数値型の要約統計量

df.describe()

	気化器圧力_PV	気化器圧力_SV	気化器圧力_MV	気化器液面レベル_PV	気化器液面レベル_SV	...	反応器流入組成（HAc）_PV	セパレータ蒸気排出量_MV (Fixed)	アブソーバスクラブ流量_MV (Fixed)	アブソーバ還流流量_MV (Fixed)	気化器液体流入量_MV (Fixed)
count	86401.000000	86401.000000	86401.000000	86401.000000	86401.0	...	86401.000000	86401.0000	86401.000000	86401.000000	8.640100e+04
mean	128.003572	128.003523	18.739939	0.699817	0.7	...	0.109531	16.1026	15.119812	0.755994	2.192400e+00
std	0.730975	0.528019	0.271741	0.001456	0.0	...	0.000585	0.0000	0.005893	0.015588	4.440918e-16
min	124.867305	126.117504	17.630283	0.691872	0.7	...	0.107004	16.1026	14.119800	0.726000	2.192400e+00
25%	127.516310	127.638645	18.556992	0.699350	0.7	...	0.109156	16.1026	15.119800	0.746000	2.192400e+00
50%	128.019870	128.032549	18.740014	0.699983	0.7	...	0.109523	16.1026	15.119800	0.756000	2.192400e+00
75%	128.514749	128.406929	18.923368	0.700589	0.7	...	0.109894	16.1026	15.119800	0.766000	2.192400e+00
max	130.558771	129.371837	19.971127	0.705129	0.7	...	0.112957	16.1026	16.119800	0.786000	2.192400e+00

8 rows × 91 columns

変動が微少な列の除外#

兎にも角にも、変動がない（ごく小さい）列はそもそも推定に寄与できないのでバサッと切り捨てます。変動がないことをどう定義するかは課題ですが、ここでは正規化を行った後の各列のパーセンタイルと閾値で判断することにしましょう。

列ごとに平均0、分散1で正規化
- まずは各列のスケールを揃えます
共通の判断基準となるパーセンタイルと閾値を決めて、条件を満たす列を説明変数から外す
- 具体的には、パーセンタイルの絶対値が閾値以下になる列を説明変数から外します

# 正規化を行う
from sklearn.preprocessing import StandardScaler

# 正規化を行うオブジェクトを生成
ss = StandardScaler()

# fit_transform関数は、fit関数（正規化するための前準備の計算）と
# transform関数（準備された情報から正規化の変換処理を行う）の両方を行う
df = pd.DataFrame(ss.fit_transform(df), index=df.index, columns=df.columns)

【パーセンタイルとは】

数値データを小さい順に並べたとき、 小さい方から数えて全体のp%に位置する値をp%点（パーセンタイル） と言います。

正規化を行った結果、理想的な各列の値の分布は標準正規分布に従っていると仮定してみます。
標準正規分布では、\([-\infty, 1.0]\)の間に、約84%のデータが含まれています。すなわち標準正規分布の84%点はおよそ1.0と考えることができます。

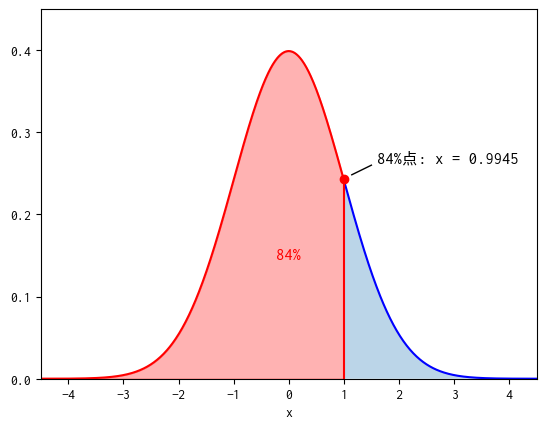
percentile

同様に考えると標準正規分布の16%点はおよそ-1.0となります。

一方、ほとんど変動がない列では、正規化を行うと多くの値が平均0付近にギュッと押し込まれることになります。
その結果、分布の峰は標準正規分布に比べ急峻になり、16%点は-1.0よりもかなり大きな値に、84%点は1.0よりもかなり小さな値になってしまうことが予想されます。

例えば 有機生成物流量_MV の16%点と84%点を確認すると

df["有機生成物流量_MV"].quantile([0.16, 0.84])

0.16   -0.579879
0.84    0.589463
Name: 有機生成物流量_MV, dtype: float64

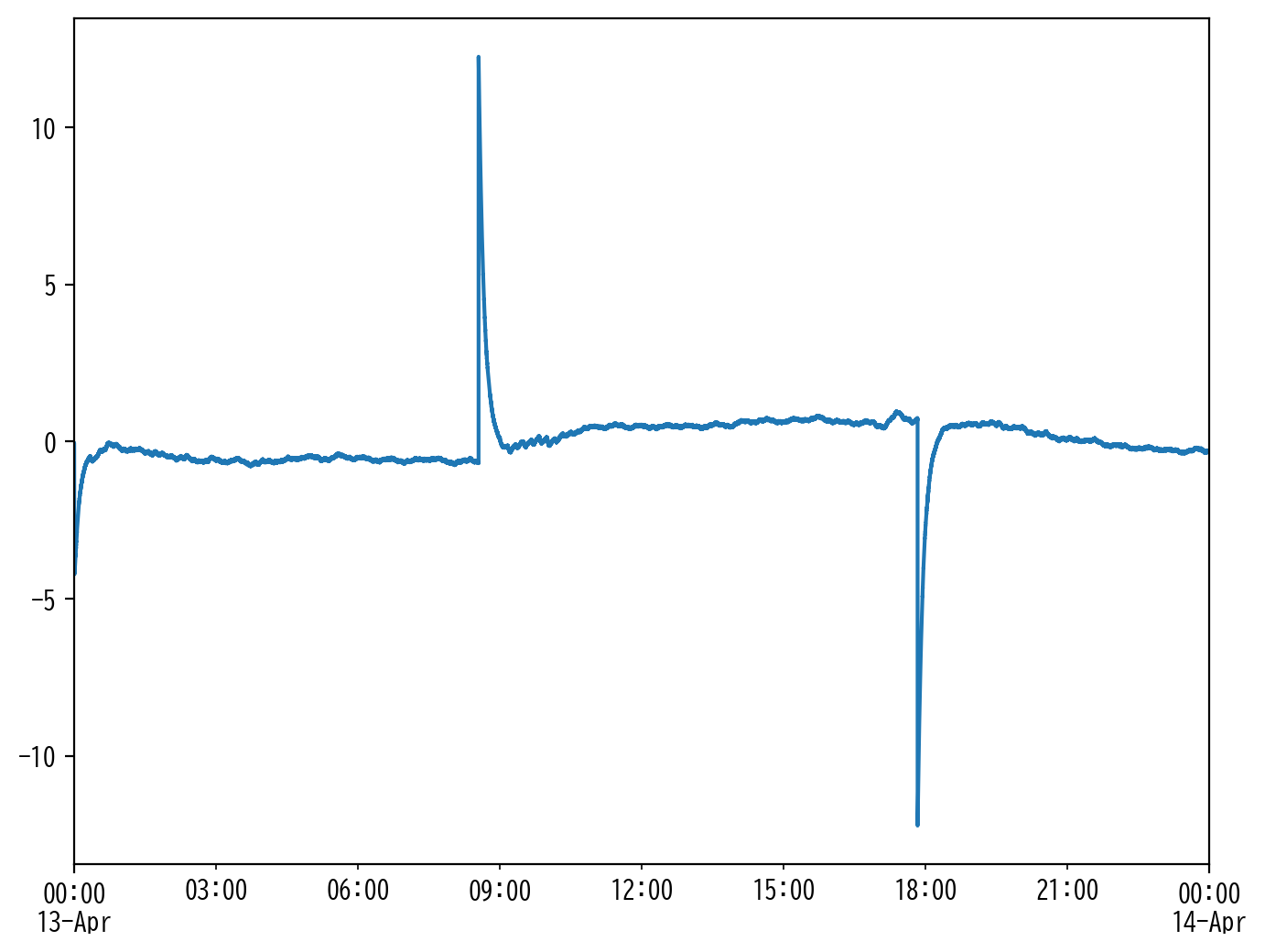
であり、実際に 有機生成物流量_MV をプロットしてみると、全体的に変動が少ない（一定値の期間が長い）ことがわかります。

plt.figure(figsize=[8, 6], dpi=200)
df["有機生成物流量_MV"].plot()

<Axes: >

../_images/4bac7d0aca2247cfa699fdfd53f2f75290684895dbbffb58e8d83a4c571699a9.png

さて、このような基準で変動のない（ごく小さい）列を切り捨てるには、基準となる

パーセンタイル
閾値

の値を適切に設定する必要があります。
さすがに一切変動がない（分散が0である）列は問答無用で切り捨てていいと思いますが、それ以外の列をどの程度まで許容し、どの程度から切り捨てるかは一概に決めつけることはできません。実務的には案件個々のドメイン知識や、解きたい問題設定などを考慮して、解析者のセンスで判断基準の値を決定していくことになります。

変動のない列をパーセンタイルと閾値で判断するときは、次のようなヒートマップを描画してデータ全体の傾向を意識することが、基準となる値を決定するのに役立つかもしれません。

横軸：パーセンタイル (1-p%点とp%点)
縦軸：閾値
色：パーセンタイルの絶対値が閾値以下となる列の数が、列の総数に占める割合
- ここでは (abs(1-p%点) < 閾値) or (abs(p%点) < 閾値) = TRUE となる列の割合

threshold = np.round(np.arange(0.03, 0.93, 0.03), decimals=2)
percentile = np.round(np.arange(0.70, 1.0, 0.01), decimals=2)
score = np.zeros([len(threshold), len(percentile)])
for i, t in enumerate(threshold):
    for j, p in enumerate(percentile):
        score[i, j] = np.sum(np.any(np.abs(df.quantile([1 - p, p])) < t, axis=0))
score = score / df.shape[1]

plt.figure(figsize=[16, 12], dpi=200)
sns.heatmap(score[::-1], square=True, cmap="pink")
plt.yticks(
    np.linspace(0.0, len(threshold) - 0.5, len(threshold))[::-1],
    [str(t).ljust(4, "0") for t in threshold],
    rotation=0,
)
plt.xticks(
    np.linspace(0.5, len(percentile) - 0.5, len(percentile)),
    [str(int((1 - p) * 100)) + "%\n" + str(int(p * 100)) + "%" for p in percentile],
    rotation=0,
)
plt.ylabel("threshold", fontsize=20)
plt.xlabel("abs(percentile)", fontsize=20)
plt.title("abs(percentile)がthreshold以下の列の数/列の総数", fontsize=20)
plt.show()

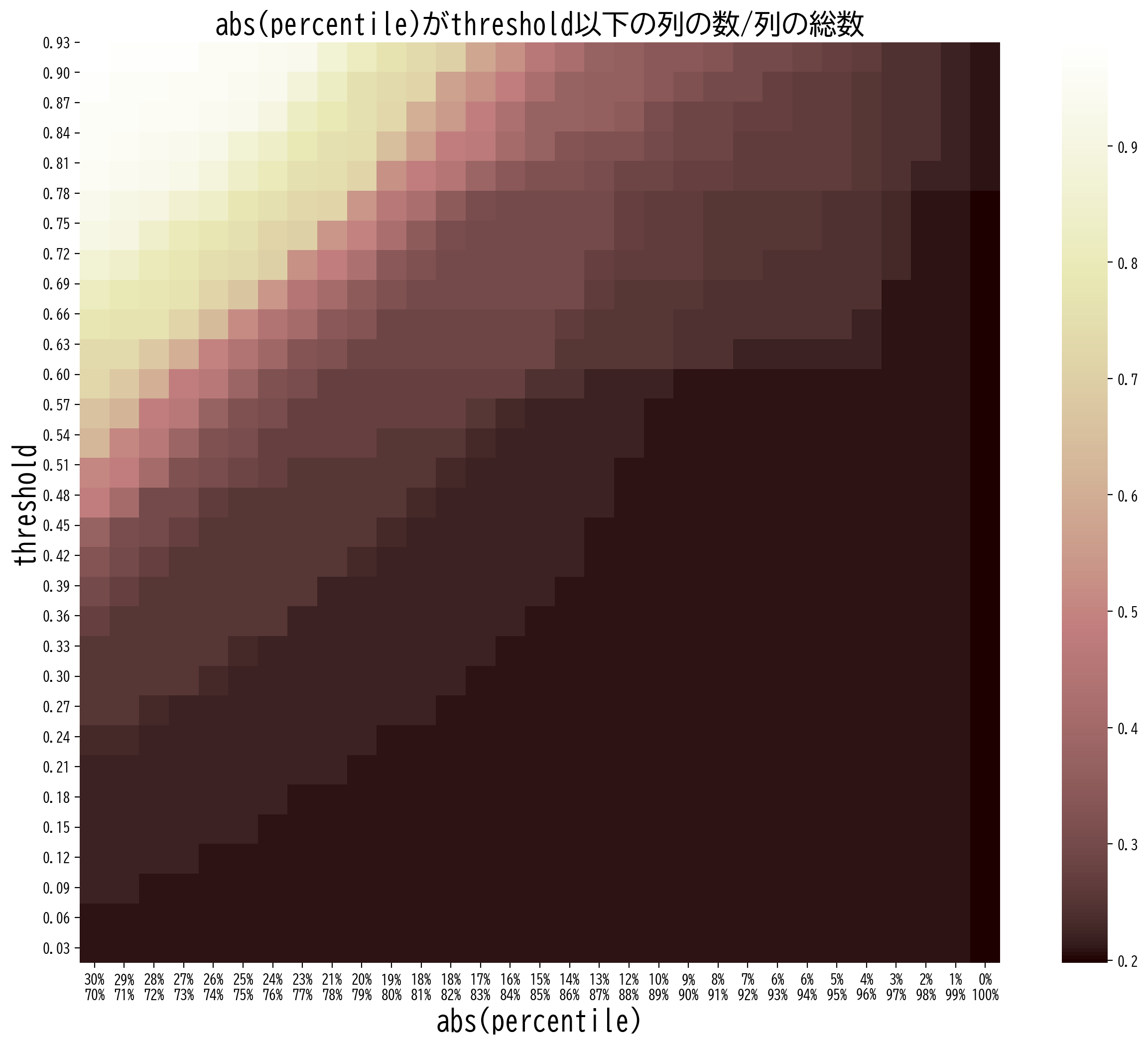
../_images/684978ea264be8bfe63135dbaacc754ac8e911868958839065793a8573c842fe.png

このヒートマップから、基準となるパーセンタイルと閾値の値をどう設定すればどれだけの列が説明変数から外されるかを大まかに読み取ることができます。例えば、16%点の絶対値もしくは84(=100-16)%点の絶対値のどちらかが閾値0.8以下となっている列は、全体の30%程度存在していると読み取ることができます。
ここでは雑に25%点の絶対値もしくは75(=100-25)%点の絶対値のどちらかが、閾値0.5以下となっている列を取り除きたいと思います。この操作だと列の総数は約20%削減されます。
今回は列がとても多いこともあり、かなりざっくりした判断基準で行いましたが、実際はもっと慎重にやるべき操作です。

df = df.iloc[
    :, list(np.logical_not(np.any(np.abs(df.quantile([0.25, 0.75])) < 0.5, axis=0)))
]

df.describe()

	気化器圧力_PV	気化器圧力_SV	気化器圧力_MV	気化器液面レベル_MV	気化器温度_PV	...	反応器流入組成（C2H6）_PV	反応器流入組成（VAc）_PV	反応器流入組成（H2O）_PV	反応器流入組成（HAc）_PV	アブソーバ還流流量_MV (Fixed)
count	8.640100e+04	8.640100e+04	8.640100e+04	8.640100e+04	8.640100e+04	...	8.640100e+04	8.640100e+04	8.640100e+04	8.640100e+04	8.640100e+04
mean	1.934167e-14	-2.802664e-16	-4.259630e-15	2.842138e-15	5.926582e-14	...	8.210621e-15	2.000023e-16	-1.164487e-15	9.458662e-15	-7.698115e-15
std	1.000006e+00	1.000006e+00	1.000006e+00	1.000006e+00	1.000006e+00	...	1.000006e+00	1.000006e+00	1.000006e+00	1.000006e+00	1.000006e+00
min	-4.290549e+00	-3.571901e+00	-4.083522e+00	-2.674138e+00	-4.530786e+00	...	-3.045583e+00	-2.060108e+00	-2.155344e+00	-4.321566e+00	-1.924147e+00
25%	-6.665944e-01	-6.910364e-01	-6.732396e-01	-7.100772e-01	-6.644850e-01	...	-6.405547e-01	-6.327078e-01	-6.219211e-01	-6.428003e-01	-6.411300e-01
50%	2.229663e-02	5.497196e-02	2.787542e-04	-4.363395e-01	5.607568e-03	...	-5.561787e-02	5.166795e-02	-1.727655e-01	-1.476343e-02	3.786639e-04
75%	6.993132e-01	7.640027e-01	6.750195e-01	1.050460e+00	6.757835e-01	...	5.793461e-01	7.856629e-01	5.161618e-01	6.193945e-01	6.418873e-01
max	3.495623e+00	2.591426e+00	4.530761e+00	1.874977e+00	4.991007e+00	...	2.997263e+00	2.032134e+00	3.652417e+00	5.857285e+00	1.924905e+00

8 rows × 68 columns

多重共線性の回避（相関係数編）#

ほとんど変動がない列を削減しても、冒頭で述べたように多重共線性を発生させる列が含まれていれば、一般に学習はうまくいきません。
まずは素直に統計量をジッと睨んで、多重共線性を孕んだ列を取り除いてみます。
さまざまなやり方やアイディアがあると思いますが、ここでは例として以下のような方針で行ってみます。

相関関係が強すぎる列はひとつにまとめて、代表として並び順の若い者を使用し、それ以外は説明変数から外す。
- これもどう定義するか課題ですが、ここでは相関係数の絶対値が0.9以上を多重共線性の危険性があるとみなすことにします。

# 相関行列の要素のうち、条件を満たすものを要素を1、満たしていない要素を0とする、隣接行列を取得する。
# ここでは、後の計算の簡略化のために対角成分も残したまま取り扱う。
Adjacency = np.array(df.corr().abs() > 0.9).astype("int")

# グラフ理論によると隣接行列のべき乗（ただし非ゼロ要素は都度すべて1に変換する）は、適当回数遷移した後に接続している要素を示す。
# 例えばi行の非ゼロ要素のインデックス集合は、i番目の要素と接続している要素の集合となる。
# これを利用して、先ほど定義した隣接行列から、多重共線性の危険性のある列のグループを抽出する
while True:
    Adjacency_next = np.dot(Adjacency, Adjacency).astype("int")
    Adjacency_next[Adjacency_next != 0] = 1
    if np.all(Adjacency_next == Adjacency):
        break
    else:
        Adjacency = Adjacency_next

multicol_list = [np.where(Ai)[0].tolist() for Ai in Adjacency]

# 要素が1つだけのグループ、および重複のあるグループを取り除き、インデックスの最も若い列を残して、それ以外を削減対象とする。
# 削減対象以外の残す列のインデックスを取得する。
extract_list = sorted(list(set(sum([m[:1] for m in multicol_list], []))))

# 多重共線性の危険性を排除したデータセットを得る。
df_corr = df.iloc[:, extract_list]

df_corr.describe()

	気化器圧力_PV	気化器圧力_SV	気化器圧力_MV	気化器液面レベル_MV	気化器温度_PV	...	反応器流入組成（O2）_PV	原材料O2供給量_MV	反応器流入組成（H2O）_PV	反応器流入組成（HAc）_PV	アブソーバ還流流量_MV (Fixed)
count	8.640100e+04	8.640100e+04	8.640100e+04	8.640100e+04	8.640100e+04	...	8.640100e+04	8.640100e+04	8.640100e+04	8.640100e+04	8.640100e+04
mean	1.934167e-14	-2.802664e-16	-4.259630e-15	2.842138e-15	5.926582e-14	...	-7.894828e-16	2.102656e-15	-1.164487e-15	9.458662e-15	-7.698115e-15
std	1.000006e+00	1.000006e+00	1.000006e+00	1.000006e+00	1.000006e+00	...	1.000006e+00	1.000006e+00	1.000006e+00	1.000006e+00	1.000006e+00
min	-4.290549e+00	-3.571901e+00	-4.083522e+00	-2.674138e+00	-4.530786e+00	...	-3.193416e+00	-4.226090e+00	-2.155344e+00	-4.321566e+00	-1.924147e+00
25%	-6.665944e-01	-6.910364e-01	-6.732396e-01	-7.100772e-01	-6.644850e-01	...	-6.723666e-01	-7.931597e-01	-6.219211e-01	-6.428003e-01	-6.411300e-01
50%	2.229663e-02	5.497196e-02	2.787542e-04	-4.363395e-01	5.607568e-03	...	-1.491356e-02	-2.155220e-03	-1.727655e-01	-1.476343e-02	3.786639e-04
75%	6.993132e-01	7.640027e-01	6.750195e-01	1.050460e+00	6.757835e-01	...	7.422012e-01	7.408581e-01	5.161618e-01	6.193945e-01	6.418873e-01
max	3.495623e+00	2.591426e+00	4.530761e+00	1.874977e+00	4.991007e+00	...	3.273125e+00	5.301264e+00	3.652417e+00	5.857285e+00	1.924905e+00

8 rows × 33 columns

多重共線性の回避（VIF編）#

多重共線性について、より統計的な議論を行いたい場合に役立つ指標として、分散拡大係数（variance inflation factor, VIF） というものがあります。
VIFとは最小二乗回帰分析における多重共線性の深刻さを評価する指標で、推定された回帰係数の分散が多重共線性のためにどれだけ増加したかを定量的に表現します。
これにより独立変数間の多重共線性を検出し、値が大きい場合はその変数を分析から除いた方がよいと考えられます。
一般的に使用される閾値は10であり、この閾値以上の列は分析から除かれることとなります。
ここで、注意しなければならないのはVIFが閾値を超える独立変数を一度にすべて除くことは避けたほうが良いと言うことです。
というのも、「多重共線性の回避（相関係数編）」でも行ったように、N個の列が多重共線性の関係にあったとして、取り除かれるべきはN-1個の列（どれを残すかは任意性がある）であるので、VIFを一度だけ計算した後にVIFが閾値を超える列を一括で取り除いてしまうと、N個の列すべてを捨ててしまうことになるからです。
これでは、重大な情報落ちの危険性があります。これを避けるためのナイーブなやり方として、例えば、 VIFを計算→VIF>閾値を満たす最大値の列を除去→VIFを再計算→VIF>閾値を満たす最大値の列を除去→…を繰り返し行う方法などが考えられます。

一方でこのように逐次的な処理を行うと、カラム数によっては計算時間にストレスを感じるかもしれません。
その場合の妥協案として、例えばVIF適用前に「多重共線性の回避（相関係数編）」のような軽量な次元削減手法を緩めの閾値で実施する方法などが考えられます。
仮に最小二乗法で線形回帰を行う場合、VIFの閾値10は相関係数では閾値0.95で次元削減していることと概ね一致するので、例えば相関係数の閾値を0.95より大きい値とした緩い制約で事前に次元削減を行った後、VIFによって逐次的に次元削減を行うなどが考えられます。
とは言え、一般的には相関係数とVIFでは次元削減のアプローチは異なるので、VIFで次元削減する場合には多少時間はかかっても当初の通り逐次的に処理する方が無難であると思います。

本稿では逐次的にVIFで次元削減していきます。

注意

statsmodelsに実装されているVIF計算関数statsmodels.stats.outliers_influence.variance_inflation_factorは、VIFの計算過程で行う線形回帰にて切片を考慮していないため、平均\(0\)に中心化されていないデータに対しては多重共線性をうまく検出できない。（statsmodelsバージョン0.14.1にて確認）

from sklearn.linear_model import LinearRegression


def VIF(X):
    X = np.asarray(X)
    n_features = X.shape[1]

    vif = np.zeros(n_features)
    for i in range(n_features):
        mask = np.arange(n_features) != i
        r2 = LinearRegression().fit(X[:, mask], X[:, i]).score(X[:, mask], X[:, i])
        if r2 == 1.0:
            vif[i] = np.inf
        else:
            vif[i] = 1.0 / (1.0 - r2)
    return vif

# vifを計算する
vif = pd.DataFrame()
vif["VIF Factor"] = VIF(df)
vif.index = df.columns
vif

	VIF Factor
気化器圧力_PV	10.307600
気化器圧力_SV	inf
気化器圧力_MV	70.274806
気化器液面レベル_MV	196.329650
気化器温度_PV	2.424255
...	...
反応器流入組成（C2H6）_PV	inf
反応器流入組成（VAc）_PV	inf
反応器流入組成（H2O）_PV	inf
反応器流入組成（HAc）_PV	inf
アブソーバ還流流量_MV (Fixed)	5.499071

68 rows × 1 columns

すべてのVIFが閾値を下回るまで、VIFの計算と列の除去を交互に繰り返します。

# VIFの計算と列の除去を交互に繰り返す
while True:
    df_vif = df[vif.index].copy()
    vif["VIF Factor"] = VIF(df_vif)
    if vif["VIF Factor"].max(axis=0) > 10:
        vif = vif.drop(vif["VIF Factor"].idxmax(axis=0), axis=0)
    else:
        break

vif

	VIF Factor
気化器圧力_PV	6.013501
気化器圧力_MV	1.942894
気化器温度_PV	2.339506
気化器ヒータ出口温度_SV	4.532047
熱交換器出口温度（リサイクルガス）_PV	8.259173
...	...
反応器流入組成（O2）_SV	1.882103
反応器流入組成（C2H6）_PV	4.185451
反応器流入組成（H2O）_PV	5.577524
反応器流入組成（HAc）_PV	3.684802
アブソーバ還流流量_MV (Fixed)	5.287608

29 rows × 1 columns

df_vif.describe()

	気化器圧力_PV	気化器圧力_MV	気化器温度_PV	気化器ヒータ出口温度_SV	熱交換器出口温度（リサイクルガス）_PV	...	反応器流入組成（O2）_SV	反応器流入組成（C2H6）_PV	反応器流入組成（H2O）_PV	反応器流入組成（HAc）_PV	アブソーバ還流流量_MV (Fixed)
count	8.640100e+04	8.640100e+04	8.640100e+04	8.640100e+04	8.640100e+04	...	8.640100e+04	8.640100e+04	8.640100e+04	8.640100e+04	8.640100e+04
mean	1.934167e-14	-4.259630e-15	5.926582e-14	4.694791e-15	-6.031649e-15	...	-4.426367e-15	8.210621e-15	-1.164487e-15	9.458662e-15	-7.698115e-15
std	1.000006e+00	1.000006e+00	1.000006e+00	1.000006e+00	1.000006e+00	...	1.000006e+00	1.000006e+00	1.000006e+00	1.000006e+00	1.000006e+00
min	-4.290549e+00	-4.083522e+00	-4.530786e+00	-1.846600e+00	-1.676561e+00	...	-2.339569e+00	-3.045583e+00	-2.155344e+00	-4.321566e+00	-1.924147e+00
25%	-6.665944e-01	-6.732396e-01	-6.644850e-01	-7.968420e-01	-7.630982e-01	...	-6.742344e-01	-6.405547e-01	-6.219211e-01	-6.428003e-01	-6.411300e-01
50%	2.229663e-02	2.787542e-04	5.607568e-03	3.308390e-02	-6.206304e-01	...	-5.053243e-02	-5.561787e-02	-1.727655e-01	-1.476343e-02	3.786639e-04
75%	6.993132e-01	6.750195e-01	6.757835e-01	7.191430e-01	9.176595e-01	...	7.502411e-01	5.793461e-01	5.161618e-01	6.193945e-01	6.418873e-01
max	3.495623e+00	4.530761e+00	4.991007e+00	1.754891e+00	2.463141e+00	...	1.734371e+00	2.997263e+00	3.652417e+00	5.857285e+00	1.924905e+00

8 rows × 29 columns

また本項の発展として、重度の多重共線性には次のような処理も有効です。

多項式を適合している場合は、予測変数の値から予測変数の平均を引く。
高い相関を持つ予測変数をモデルから取り除く。これらの予測変数は冗長な情報を提供しているため、取り除いてもR2は大して減少しない。取り除く方法としては、ステップワイズ回帰、ベストサブセット回帰、データセットに関する専門知識などが使用できる。
PLSまたは主成分分析を使用する。これらの分析法を利用することで、予測変数の数を減らして、より小さい一連の無相関な成分にまとめられる。

小括#

本項では次元削減の手法を主に多重共線性の観点からまとめてみました。
次元削減の目的は、学習に寄与しない、あるいは悪影響を与える列を削減することにありますが、過って重要な情報を含む列まで消してしまうと元も子もありません。
本項はあくまでも単なる方法論であることを強く意識し、実際の案件では、ドメイン知識や系のダイナミクス（因果グラフなど）を駆使してケース・バイ・ケースで対処することが重要です。
※冒頭でも述べたように本項では「次元削減」についての記事です。「次元圧縮（前編：主成分分析）」＆「次元圧縮（後編：その他の手法）」の方の記事も併せてご参照ください。

次元削減

目次