分類モデルの評価#
分類問題においても複数のモデルやハイパーパラメータを比較する上で数値的な評価指標が必要であることは変わりませんが、その実際は回帰問題の場合より若干複雑です。これは機械学習で用いられる多くの分類モデルが直接的にはラベルそのものでなく各ラベルを取る確率を予測することにもよりますし、確率・統計的解析のみが行われていた時代から用いられている指標には二値分類の問題にのみ対応したものが少ないことにもよります。加えてこれらの伝統的な指標は情報検索・疫学・異常検知など応用先の分野によって異なる名称で呼ばれていることもあり、用語の混乱に拍車をかけています。
本稿では、分類モデル一般で利用される基本的な評価指標について説明した上で、特に二値分類の評価指標を異常検知の評価指標として利用する際の注意点について簡単に言及します。回帰モデルで利用される評価指標、また統計的機械学習における尤度・汎化誤差・情報量規準などの概念についての詳細な説明はそれぞれ当該項目を参照してください。
準備#
分類モデル \(f: \mathcal{X} \to \mathcal{C}\) とデータ \(\mathcal{D} = ( (x_i, y_i) ) _{i = 1, \ldots, n} \in ( \mathcal{X} \times \mathcal{C} ) ^n\) が与えられているものとします。ここで \(\mathcal{X}\) は説明変数の定義域で、 \(\mathcal{C} = \{0, \ldots, K - 1 \}\) はラベルの集合です。このとき、分類モデルの予測したラベル \(\hat{\mathbf{y}} = ( \hat{y}_i ) _{i = 1, \ldots, n} = ( f (x_i) ) _{i = 1, \ldots, n}\) が対応する真のラベル \(\mathbf{y} = ( y_i ) _{i = 1, \ldots, n}\) とどの程度一致しているのかの指標が計算できれば、このデータに対する分類モデルの当てはまりの良さの指標として利用できそうです。
一方で、こうしたラベルの情報だけを用いた評価指標は分類モデルを学習する過程だと利用しにくい場合も多々あります。実際、機械学習で利用される分類モデルの多くは入力 \(x_i\) に対してラベルの予測 \(\hat{y}_i\) を直接出力するのではなく、まず各ラベルを取る確率 \(\hat{\mathbf{p}}_i = ( \hat{p}_{i, k} )_{k = 0, \ldots, K - 1} \in \mathbf{S}_{K - 1}\) を出力し、そのうちで最も確率の高いもの \(\hat{y}_i = \arg \max_k \hat{p}_{i, k}\) をラベルの予測とするものになっています。ただし \(\mathbf{S}_{K - 1} = \{ (q_0, \ldots, q_{K - 1}); \forall q_k \ge 0, \sum_{k = 0}^{K - 1} q_k = 1 \}\) は確率単体とします。この確率を出力する関数 \(g: \mathcal{X} \to \mathbf{S}_{K - 1}\) のパラメータを学習するために、真のラベル \(y_i\) を
として \(\mathbf{p}_i = ( p_{i, k} )_{k = 0, \ldots, K - 1} \in \mathbf{S}_{K - 1}\) に変換( one-hot encoding などと呼びます)します。適当な関数 \(L: \mathbf{S}_{K - 1}^n \times \mathbf{S}_{K - 1}^n \to \mathbf{R}\) で \(( \hat{\mathbf{p}}_i )_i\) が \(( \mathbf{p} )_i\) によく当てはまっているほど \(L ( ( \mathbf{p}_i )_i, ( \hat{\mathbf{p}}_i )_i )\) の値が小さくなるような関数を考え、その値を(主に学習の過程における)データに対する分類モデルの当てはまりの良さの指標として利用できます。
本稿ではこれら二種類の評価指標の双方で代表的なものを解説すると共に、特に二値分類( \(K = 2\) の場合)の特殊なケースとして異常検知問題におけるモデルの評価方法について解説します。
import numpy as np
以降の例において、 \(\mathbf{y}\) および \(( \hat{\mathbf{p}}_i )_i\) の値としてはダミーの乱数列を利用し、 \(\hat{\mathbf{y}}\) は \(\hat{y}_i = \arg \max_k \hat{p}_{i, k}\) によって定めるものとします。
n = 50 # サンプル数
K = 5 # 多値分類の場合のラベル数
rng = np.random.default_rng(seed=42)
# 二値分類の場合
yb = rng.choice(a=np.arange(2), size=(n,)) # 真のラベルの値
pb_hat = rng.dirichlet(alpha=np.full(shape=(2,), fill_value=1.), size=(n,)) # モデルの予測した確率
yb_hat = np.argmax(pb_hat, axis=1) # モデルの予測したラベルの値
# 多値分類の場合
y = rng.choice(a=np.arange(K), size=(n,)) # 真のラベルの値
p_hat = rng.dirichlet(alpha=np.full(shape=(K,), fill_value=1.), size=(n,)) # モデルの予測した確率
y_hat = np.argmax(p_hat, axis=1) # モデルの予測したラベルの値
ラベルの値 \(\mathbf{y}\) のone-hot encodingについては np.eye で生成した単位行列を並び替えても良いですし、scikit-learnの OneHotEncoder クラスを用いることもできます。
from sklearn.preprocessing import OneHotEncoder
# NumPyのみを使う場合
# pb = np.eye(2)[yb] # ybが(n,)-shapedの整数型なので、これを用いて2x2-単位行列の行を並び替える
# p = np.eye(K)[y] # 多値分類の場合も同様
# scikit-learnを使う場合
## 二値分類の場合
transformer_b = OneHotEncoder(
categories=[np.arange(2)], # リストのリストを渡す;複数列を同時にencodingする場合は列毎のラベル一覧
sparse=False, # デフォルトではsparse=Trueで疎行列形式を返す
).fit(yb.reshape(-1, 1))
pb = transformer_b.transform(yb.reshape(-1, 1))
## 多値分類の場合
transformer = OneHotEncoder(
categories=[np.arange(K)],
sparse=False,
).fit(y.reshape(-1, 1))
p = transformer.transform(y.reshape(-1, 1))
混同行列#
真のラベルと予測したラベルの値の組 \(( y_i, \hat{y}_i )\) を集計した値
を成分とした行列 \(( C_{k, k'} )_{k, k'}\) を 混同行列 (confusion matrix) と呼びます。ただし \(1_P\) は命題 \(P\) が真の場合のみ \(1\) を取り、そうでなければ \(0\) を取るものとします。混同行列の対角成分 \(( C_{k, k} )_k\) は予測が正解した標本に、非対角成分はそうでない標本に対応しています。
NumPyのみを用いる場合は、例えば次のように計算できます。
# 混同行列を作る関数
def create_cmat(y_true, y_pred, n_labels):
indices, values = np.unique(
np.concatenate([y_true[..., np.newaxis], y_pred[..., np.newaxis]], axis=-1), # (n, 2)-shapedの配列
return_counts=True,
axis=0,
) # indicesにはラベルの値の組が、valuesにはその組の個数がそれぞれ格納される
cmat = np.zeros(shape=(n_labels, n_labels), dtype=int) # 混同行列を格納する配列を初期化
for index, value in zip(indices, values):
cmat[index[0], index[1]] = value # 混同行列の非ゼロの各成分を格納
return cmat
cmat_b = create_cmat(yb, yb_hat, n_labels=2)
cmat = create_cmat(y, y_hat, n_labels=K)
print('NumPy Result::')
print('Confusion matrix (two-class):')
print(cmat_b)
print('Confusion matrix (multi-class):')
print(cmat)
NumPy Result::
Confusion matrix (two-class):
[[12 9]
[15 14]]
Confusion matrix (multi-class):
[[2 3 2 2 3]
[3 4 1 0 0]
[6 2 3 5 1]
[1 1 2 1 1]
[0 1 3 1 2]]
scikit-learnでは confusion_matrix 関数を用いれば簡単に混同行列を計算できます。 confusion_matrix 関数では第一引数(真のラベルの値 \(\mathbf{y}\) を与えることを想定)が行方向、第二引数(予測したラベルの値 \(\hat{\mathbf{y}}\) を与えることを想定)が列方向に対応した混同行列が返されます。ラベルの値を並べる順序はキーワード引数 labels で指定でき、 \(\mathbf{y}\) や \(\hat{\mathbf{y}}\) に現れないラベルがある場合にもこの引数を利用することになります。
from sklearn.metrics import confusion_matrix
cmat_b_ = confusion_matrix(yb, yb_hat, labels=[0, 1])
cmat_ = confusion_matrix(y, y_hat, labels=np.arange(K))
print('scikit-learn Result')
print('Confusion matrix (two-class):')
print(cmat_b_)
print('Confusion matrix (multi-class):')
print(cmat_)
scikit-learn Result
Confusion matrix (two-class):
[[12 9]
[15 14]]
Confusion matrix (multi-class):
[[2 3 2 2 3]
[3 4 1 0 0]
[6 2 3 5 1]
[1 1 2 1 1]
[0 1 3 1 2]]
また、scikit-laernでは ConfusionMatrixDisplay クラスを用いれば上記のように計算した混同行列を可視化できます。そして、今回は省きますが分類モデル \(f\) のオブジェクト( BaseClassifier 型を継承しているもの)が利用できる場合は plot_confusion_matrix 関数によって混同行列を直接描画することも可能です。
from sklearn.metrics import ConfusionMatrixDisplay
# from sklearn.metrics import plot_confusion_matrix
cmat_b_disp_ = ConfusionMatrixDisplay(cmat_b_)
cmat_b_disp_.plot()
cmat_disp_ = ConfusionMatrixDisplay(cmat_)
cmat_disp_.plot()
<sklearn.metrics._plot.confusion_matrix.ConfusionMatrixDisplay at 0x11d452a60>
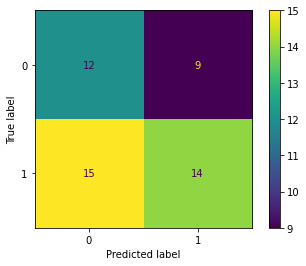
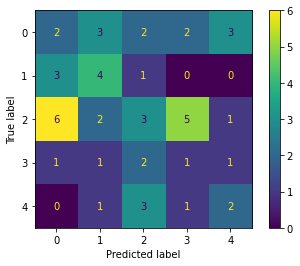
二値分類の混同行列#
二値分類の問題で各ラベルが陰性 (negative) および陽性 (positive) に対応すると思える場合、混同行列の各成分 \(C_{k, k'}\) には特別な名称がつけられています。いま仮にラベル \(k = 0\) を陰性、 \(k = 1\) を陽性と思った場合の各成分の名称は次の通りです。
\(\hat{y}_i = 0\) |
\(\hat{y}_i = 1\) |
|
|---|---|---|
\(y_i = 0\) |
\(C_{0, 0}\) |
\(C_{0, 1}\) |
\(y_i = 1\) |
\(C_{1, 0}\) |
\(C_{1, 1}\) |
このとき、数式中でも \(\mathit{TN} = C_{0, 0}\) などのように混同行列の各成分を英字の略称によって表記することがあります。
print(f'TN: {cmat_b[0, 0]}, FP: {cmat_b[0, 1]}, FN: {cmat_b[1, 0]}, TP: {cmat_b[1, 1]}.')
TN: 12, FP: 9, FN: 15, TP: 14.
分類モデルの評価指標#
本節では主要な分類モデルの評価指標をいくつか紹介し、併せてそれらのNumPyおよびscikit-learnにおける計算方法を示します。
Accuracy#
Accuracyとは
で与えられる値のことです。Accuracyはすべての標本のうちモデルの予測したラベルが真のラベルと一致している標本の割合を表す指標で、 \(0\) から \(1\) の間の値を取り、値が \(1\) に近いほどモデルがよく当てはまっていることを示します。
NumPyのみを用いる場合は次のように計算できます。
acc_b = np.mean(yb == yb_hat)
acc = np.mean(y == y_hat)
print('NumPy Result::')
print(f'Accuracy (two-class): {acc_b}.')
print(f'Accuracy (multi-class): {acc}.')
NumPy Result::
Accuracy (two-class): 0.52.
Accuracy (multi-class): 0.24.
scikit-learnでは accuracy_score 関数を用いてaccuracyの値を計算できます。
from sklearn.metrics import accuracy_score
acc_b_ = accuracy_score(yb, yb_hat)
acc_ = accuracy_score(y, y_hat)
print('scikit-learn Result::')
print(f'Accuracy (two-class): {acc_b_}.')
print(f'Accuracy (multi-clas): {acc_}.')
scikit-learn Result::
Accuracy (two-class): 0.52.
Accuracy (multi-clas): 0.24.
Precision / Recall / F値#
これらの指標は本来二値分類の問題で各ラベルが陰性 (negative) および陽性 (positive) に対応すると思える場合について導入された指標です。このうち適合率 (precision) と再現率 (recall) はそれぞれ
と定義されます。即ち、precisionはモデルが陽性と予測した標本のうち真に陽性である標本の割合を、recallは真に陽性である標本のうちモデルが陽性であると予測した標本の割合を表す指標です。疫学などにおいてrecallは感度 (sensitivity) とも呼ばれます。いずれの指標も \(0\) から \(1\) の間の値を取り、値が \(1\) に近いほどモデルがよく当てはまっていることを示します。
また、F値 (F-score, F-measure) はprecisionとrecallの調和平均
として定義されます。これを拡張して、precisionよりrecallを \(\beta\) 倍だけ重視する場合の重み付き調和平均
としたものが利用されることもあります(調和平均の重みとして \(\beta^2\) を利用するのは歴史的な経緯によるものです)。F値は \(0\) から \(1\) の間の値を取り、値が \(1\) に近いほどモデルがよく当てはまっていることを示します。
NumPyのみを用いる場合は、例えば次のように計算できます。
# 事前に混同行列を計算している場合
# tn, fp, fn, tp = cmat_b[0, 0], cmat_b[0, 1], cmat_b[1, 0], cmat_b[1, 1]
#
# prec_b = tp / (tp + fp)
# recall_b = tp / (tp + fn)
# f1_b = 2*tp / (2*tp + fp + fn)
# 直接計算する場合
tp_ = ((yb == 1) & (yb_hat == 1)).sum()
tp_fp_ = (yb_hat == 1).sum() # TP+FP, モデルが陽性と予測した標本の総数
tp_fn_ = (yb == 1).sum() # TP+FN, 真に陽性である標本の総数
prec_b = tp_ / tp_fp_ # precision
recall_b = tp_ / tp_fn_ # recall
f1_b = 2*tp_ / (tp_fp_ + tp_fn_) # F-score (beta=1)
# beta = 2.
# f2_b = (1 + beta**2)*tp_ / (tp_fp_ + beta**2 * tp_fn_) # F-score (beta=2)
print('NumPy Result::')
print(f'Precision (two-class): {prec_b}.')
print(f'Recall (two-class): {recall_b}.')
print(f'F-score (two-class): {f1_b}.')
NumPy Result::
Precision (two-class): 0.6086956521739131.
Recall (two-class): 0.4827586206896552.
F-score (two-class): 0.5384615384615384.
scikit-learnでは precision_score をはじめとしてこれらの指標を計算するための関数が用意されています。
from sklearn.metrics import precision_score, recall_score, f1_score
prec_b_ = precision_score(yb, yb_hat) # precision
recall_b_ = recall_score(yb, yb_hat) # recall
f1_b_ = f1_score(yb, yb_hat) # F-score (beta=1)
# f1_b_ = fbeta_score(yb, yb_hat, beta=1.) # F-score (beta=1)
# f2_b_ = fbeta_score(yb, yb_hat, beta=2.) # F-score (beta=2)
print('NumPy Result::')
print(f'Precision (two-class): {prec_b_}.')
print(f'Recall (two-class): {recall_b_}.')
print(f'F-score (two-class): {f1_b_}.')
NumPy Result::
Precision (two-class): 0.6086956521739131.
Recall (two-class): 0.4827586206896552.
F-score (two-class): 0.5384615384615384.
これらの指標が多値分類の場合に拡張されて利用されることもありますが、詳細は例えばscikit-learnのUser Guideなどをご参照ください。
Sensitivity / Specificity / ROC / AUC#
これらの指標も二値分類の問題で各ラベルが陰性 (negative) および陽性 (positive) に対応すると思える場合について導入された指標です。モデルの感度 (sensitivity) 、特異度 (specificity) および偽陽性率 (false positive rate, FPR) をそれぞれ
と定義します。感度と再現率 (recall) は同一の指標です。感度は真に陽性である標本のうちモデルが陽性であると予測した標本の割合、特異度は真に陰性である標本のうちモデルが陰性であると予測した標本の割合、また偽陽性率は真に陰性である標本のうちモデルが誤って陽性であると予測した標本の割合を指します。
いま分類のプロセスに何か1次元のハイパーパラメータがあり、その値によって分類の結果を操作できるものとします。例えばモデルが入力 \(x_i\) に対してまず各ラベル(陰性 \(0\) および陽性 \(1\) )を取る確率 \(\hat{\mathbf{p}}_i = ( \hat{p}_{i, 0}, \hat{p}_{i, 1} ) = ( \hat{p}_{i, 0}, 1 - \hat{p}_{i, 0} )\) を出力するものとし、ハイパーパラメータとして閾値 \(\theta \in (0, 1)\) を設けて
によってラベルの予測 \(\hat{y}_i\) を定めている場合などがこれに相当します。なお、 \(\theta = 1/2\) とすれば( \(\hat{p}_{0, 1} = 1/2\) の場合を除いて) \(\hat{y}_i = \arg \max_k \hat{p}_{i, k}\) によって定めていることと同等になります。受信者操作特性曲線 (reciever operation characteristic curve, ROC curve, ROC曲線) とは横軸に偽陽性率、縦軸に感度を取ったときのこのハイパーパラメータによる媒介曲線のことです。
(図はWikimedia commonsより引用)
前述の例のように閾値 \(\theta\) をハイパーパラメータとする場合、ROC曲線は2点 \((0, 0)\) および \((1, 1)\) を通る単調増加の曲線になります。感度は高いほど良く、偽陽性率は低いほど良いのでROC曲線が上側に膨らんでいるほど(ハイパーパラメータ \(\theta\) の値を均して全体的に)良い分類モデルであるということができます。この観点から、ROC曲線より下側の領域の面積、いわゆる曲線下面積 (area under the curve, AUC) は分類モデルの \(\theta\) の値によらない評価指標として利用できます。ROC曲線のAUCは \(0\) から \(1\) の間の値を取り、値が \(1\) に近いほどモデルがよく当てはまっていることを示します。
scikit-learnでは roc_curve 関数を用いてROC曲線の通る点を計算でき、さらに auc 関数にその返り値を渡すことでそのAUCの値を計算できます。また、ROC曲線それ自体に興味がない場合は roc_auc_score 関数を用いればROC曲線のAUCの値を直接計算することもできます。
from sklearn.metrics import roc_curve, auc
# from sklearn.metrics import roc_auc_score
# ROC曲線の描画に必要な情報を含めて計算する場合
fpr_, tpr_, thresholds_ = roc_curve(
yb, # 第1引数に真のラベルの値
pb_hat[:, 1], # 第2引数に分類器の出力したスコア
)
roc_auc_ = auc(fpr_, tpr_)
# ROC曲線のAUCのみを直接計算する場合
# roc_auc_ = roc_auc_score(yb, pb_hat[:, 1])
print(f'scikit-learn Result::')
print(f'AUC (by auc): {roc_auc_}.')
scikit-learn Result::
AUC (by auc): 0.4942528735632184.
scikit-laernでは RocCurveDisplay クラスを用いれば上記のように計算したROC曲線を可視化できます。また、今回は省きますが分類モデル \(f\) のオブジェクト( BaseClassifier 型を継承しているもの)が利用できる場合は plot_roc_curve 関数によってROC曲線を直接描画することも可能です。
from sklearn.metrics import RocCurveDisplay
# from sklearn.metrics import plot_roc_curve
roc_disp_ = RocCurveDisplay(fpr=fpr_, tpr=tpr_, roc_auc=roc_auc_)
roc_disp_.plot()
<sklearn.metrics._plot.roc_curve.RocCurveDisplay at 0x1313f46a0>
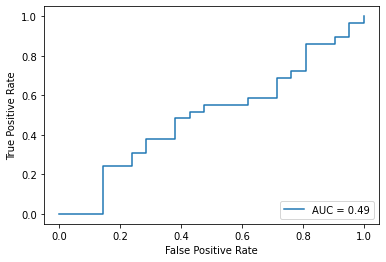
今回は \(\hat{\mathbf{p}}_i\) がランダムな予測なので、ROC曲線は概ね2点 \((0, 0), (1, 1)\) を結ぶ直線の近くを走っています。
クロスエントロピー#
この指標はこれまでに説明した各指標と異なり、真のラベルの値 \(\mathbf{y}\) (あるいはそれをone-hot encodingした \(( \mathbf{p}_i )_i\) )とモデルの予測した各ラベルを取る確率 \(( \hat{\mathbf{p}}_i )_i\) との間に定義されます。次の式で定義される値
をクロスエントロピー (cross-entropy, 交差エントロピー) またはlog lossと呼びます。クロスエントロピーは非負の値を取り、値が0に近いほどモデルがよく当てはまっていることを表します。
NumPyのみを用いる場合は次のように計算できます。
ce_b = - (pb * np.log(pb_hat)).sum(axis=1).mean()
ce = - (p * np.log(p_hat)).sum(axis=1).mean()
print('NumPy Result::')
print(f'Cross-Entropy (two-class): {ce_b}.')
print(f'Cross-Entropy (multi-class): {ce}.')
NumPy Result::
Cross-Entropy (two-class): 0.8820753531817364.
Cross-Entropy (multi-class): 2.2345673160433033.
scikit-learnでは log_loss 関数を用いてクロスエントロピーの値を計算できます。この関数は正しいラベルの値 \(\mathbf{y}\) とモデルの予測した各ラベルを取る確率 \(( \hat{\mathbf{p}}_i )_i\) の組を引数として取ることに注意してください。
from sklearn.metrics import log_loss
ce_b_ = log_loss(yb, pb_hat)
ce_ = log_loss(y, p_hat)
print('scikit-learn Result::')
print(f'Cross-Entropy (two-class): {ce_b_}.')
print(f'Cross-Entropy (multi-clas): {ce_}.')
scikit-learn Result::
Cross-Entropy (two-class): 0.8820753531817364.
Cross-Entropy (multi-clas): 2.2345673160433033.
クロスエントロピーはモデルの予測した各ラベルを取る確率 \(( \hat{\mathbf{p}}_i )_i\) を直接取り扱うこと、またそれぞれのラベルの値が確率 \(\hat{\mathbf{p}}_i\) のカテゴリカル分布に従うと仮定したときの条件付き対数尤度に対応することから分類モデルの学習時の損失関数としてよく設定されます。
異常検知の評価指標#
正常標本と異常標本を分類するタイプの異常検知問題は本質的に二値分類の問題と同じなので、評価指標についても(歴史的な経緯による用語の違いこそありますが)基本的には二値分類で利用されるものが援用されます。この場合、正常標本を「陰性」としてラベル \(0\) を割り当て、異常標本を「陽性」としてラベル \(1\) を割り当てることが一般的です。
ただし、実用上は多くの場合に正常標本の数が異常標本の数より圧倒的に多い、即ち
となる場合が多いので、通常の二値分類の問題とは指標の有効性が異なるケースもしばしばあります。例えば正常標本が990個、異常標本が10個の場合を考えると、「いかなる入力に対しても必ず正常標本と予測する」ダミーのモデルでは
となってaccuracyの指標が0.99となり、あたかも優秀なモデルであるように見えてしまいます。
正常標本精度 / 異常標本精度 / 分岐点精度#
二値分類の評価指標である特異度 (specificity) と感度 (sensitivity) の定義式
を思い出すと、異常検知ではこれらがそれぞれ正常標本、異常標本をモデルが正しく正常、異常と判定した割合に対応していることが分かります。この観点から異常検知の分野では特異度のことを正常標本精度と呼ぶことがあり、感度のことを異常標本精度、異常網羅率 (coverage)、ヒット率 (hit rate)などと呼ぶことがあります。異常検知の問題では、単純にaccuracyを利用するよりこれらの指標を参照した方が有益な場合も多々あります。
また、ROC曲線を描いたときと同様に1次元のハイパーパラメータ \(\theta\) によって異常検知(分類)の結果を操作できるとき、井出 (2015) は特異度(正常標本精度)と感度(異常標本精度)が一致するときのこれらの指標の値を分岐点精度と呼んでモデルの性能評価に利用することを提案しています。とはいえ分岐点精度を実際に求めることは煩雑なため、パラメータ \(\theta\) を動かしたときのF値(特異度と感度の調和平均)の最大値で代用することも同じく提案しています。

小括#
本稿では混同行列について説明した後で分類モデルの主要な評価指標を解説し、また二値分類の評価指標を異常検知の問題に流用する際の注意点について簡単に触れました。分類モデルの評価指標はここで解説したもの以外にもよく使われるもの(Matthews相関係数やBrierスコアなど)がありますし、二値分類向けの評価指標を多値分類に拡張する試みもいくつか行われています。いずれにせよ、回帰問題の場合と同様に評価指標の選択に絶対的な基準はありませんので、やはり分析の目的と理論上の要請に合わせて適切なものを選択する必要があります。
参考文献#
井出 (2015). 入門 機械学習による異常検知 - Rによる実践ガイド -. コロナ社.
scikit-learn User Guide

