クロスバリデーション(交差検証)#
はじめに#
回帰モデルや分類モデル(以下モデルと呼びます)を学習する目的として、
すでに収集されたデータについて、変数間の関係を分析したい場合(特に回帰分析)
学習されたモデルを未知のデータ(未来に収集されるデータなど)に適用したい場合
の2つが考えられます。
後者のような未知データへの適用を想定した場合、学習したモデルを未知データに適用した場合、どの程度の誤差で推定できるのかが興味の対象となります。システム化した時など実際の応用の場面を想定すると、このような誤差などの評価指標を手持ちのデータから見積らなければなりません。特に、複数のモデル(ハイパーパラメータを変えた場合など)で精度を比較して最適なモデルを選択したい場合などでは、本稿で扱うクロスバリデーション(交差検証)という手法をとることが一般的です。
前者のケースにおいても分析に用いられる数理モデルが適切であるかどうかを見積る方法がありますが、これについては別の稿にて扱うこととし、本稿では後者の未知データに適用する場合について、クロスバリデーションを中心に見ていきます。
※ ここでは特に回帰分析を対象とします。
Train-Test split#
まず、未知データにおける回帰分析の誤差を見積りたい場合、手持ちのデータすべてをTrainingデータとして扱い、誤差を評価してしまうと何が起こるでしょうか。データとして、scikit-learn に含まれる boston というデータの一部を使って見てみましょう。このデータセットは、sklearn.datasets.load_boston() という関数を用いて、読み込むことが出来ます。
# モジュールインポート + データの読み込み
%matplotlib inline
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.model_selection import KFold
# matplotlibでは日本語にデフォルトで対応していないので、日本語対応フォントを読み込む
plt.rcParams['font.family'] = 'BIZ UDGothic' # Windows
# plt.rcParams['font.family'] = 'Hiragino Maru Gothic Pro' # Mac
# その他使えるフォント一覧は以下のコードで取得できます。
# import matplotlib.font_manager
# [f.name for f in matplotlib.font_manager.fontManager.ttflist]
import warnings
warnings.filterwarnings('ignore')
boston = load_boston()
dfX = pd.DataFrame(boston.data, columns=boston.feature_names)
display(dfX.head())
# 説明変数
X = dfX.values
# 目的変数
Y = boston.target.reshape(-1,1)
| CRIM | ZN | INDUS | CHAS | NOX | RM | AGE | DIS | RAD | TAX | PTRATIO | B | LSTAT | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.00632 | 18.0 | 2.31 | 0.0 | 0.538 | 6.575 | 65.2 | 4.0900 | 1.0 | 296.0 | 15.3 | 396.90 | 4.98 |
| 1 | 0.02731 | 0.0 | 7.07 | 0.0 | 0.469 | 6.421 | 78.9 | 4.9671 | 2.0 | 242.0 | 17.8 | 396.90 | 9.14 |
| 2 | 0.02729 | 0.0 | 7.07 | 0.0 | 0.469 | 7.185 | 61.1 | 4.9671 | 2.0 | 242.0 | 17.8 | 392.83 | 4.03 |
| 3 | 0.03237 | 0.0 | 2.18 | 0.0 | 0.458 | 6.998 | 45.8 | 6.0622 | 3.0 | 222.0 | 18.7 | 394.63 | 2.94 |
| 4 | 0.06905 | 0.0 | 2.18 | 0.0 | 0.458 | 7.147 | 54.2 | 6.0622 | 3.0 | 222.0 | 18.7 | 396.90 | 5.33 |
データは重回帰を想定したデータとなっておりますが、説明を簡単にするため、最終列の LSTAT (列番号=12)を説明変数として、目的変数を回帰する問題を例にとります。また、分析に使うサンプル数(行数)も大幅に削減し、このデータからランダムに抽出(numpy.random.shuffle() 関数を使い、行をシャッフルします)した 20行を使うこととします。こうして得られた説明変数、目的変数(それぞれ x0, y0)を「データセット0」と呼ぶこととします。RMSE (Root Mean Squared Error) を用いてモデルの誤差を評価すると、以下の様になります。
#再現性のために乱数のseedを設定
np.random.seed(6000)
# 行をシャッフル
np.random.shuffle(X)
m = 12 # LSTAT の列番号
# 20サンプル抽出
n = 20
x0 = X[:n,[m]]
y0 = Y[:n,:]
# 線形回帰モデルの学習
model0 = LinearRegression()
model0.fit(x0, y0)
y0_pred = model0.predict(x0)
rmse0 = np.sqrt(np.mean((y0_pred - y0)**2))
print("「データセット0」全部を用いた場合: RMSE={:.3f}".format(rmse0))
「データセット0」全部を用いた場合: RMSE=5.645
しかし、この回帰モデルを未知のデータに対して適用した時、どのような誤差になるかはわかりません。未知のデータ
での誤差が知りたければ、データの一部を未知にしてしまえば良い、という考えがまず浮かぶと思います。つまり、「データセット0」を学習に使うデータとテストに使うデータとを分けるというわけです。
これは、sklearn.model_selection.train_test_split() 関数を使うことで、簡単に行うことができます。テストに使うサンプルをtest_size オプションで指定した割合になるようにランダムに選びます。
for i in range(10):
x0_tr, x0_ts, y0_tr, y0_ts = train_test_split(x0, y0, test_size=0.3, random_state=i)
model1 = LinearRegression()
model1.fit(x0_tr, y0_tr)
y0_tr_pred = model1.predict(x0_tr)
y0_ts_pred = model1.predict(x0_ts)
rmse0_tr = np.sqrt(np.mean((y0_tr_pred - y0_tr)**2))
rmse0_ts = np.sqrt(np.mean((y0_ts_pred - y0_ts)**2))
print("no split: {:.3f}, train: {:.3f} test: {:.3f}".format(rmse0, rmse0_tr, rmse0_ts))
no split: 5.645, train: 5.659 test: 6.566
no split: 5.645, train: 5.146 test: 7.764
no split: 5.645, train: 5.132 test: 7.365
no split: 5.645, train: 4.805 test: 7.812
no split: 5.645, train: 4.876 test: 7.399
no split: 5.645, train: 5.448 test: 6.121
no split: 5.645, train: 5.490 test: 6.152
no split: 5.645, train: 5.174 test: 7.079
no split: 5.645, train: 5.259 test: 6.669
no split: 5.645, train: 5.332 test: 6.944
テストの RMSE を見るとばらついていることがわかります。
基本的なクロスバリデーション#
クロスバリデーションは、未知データに対する誤差などの評価値(分類問題の場合、精度、再現率、適合率、F値など)を、単純な Training-Test split に比べて安定した評価値を見積るために使われます。
K-Fold クロスバリデーション#
下図は、最も基本的なクロスバリデーションの概要を示したものです。

手順は以下のようになります。
データを n 分割する(図は n=5 の例)。この一つ一つの分割のことを Fold と呼ぶ。
1つの Fold を検証(validation)用、残りの n-1 個の Fold をモデルの学習用に使う、というパターンを、テスト用のFoldがすべての Fold に当たるように n パターン(n split分)用意する(図においては Experiment 1 〜 Experiment 5 に相当)
それぞれの split において、回帰モデルの学習とテスト(回帰モデルをテストデータに適用し評価値[RMSEなど]を計算)
全Foldの評価値を平均して、最終的な評価値の見積りとする。
このようなクロスバリデーションのことは、K個のFoldに分割することから K-Fold クロスバリデーション と呼びます。各サンプルが独立同分布(i.i.d.)に従っている(他のサンプルの値の影響を受けない)ことが想定される場合、Foldの分割の仕方はどの様に行っても問題ありません。(一見影響を受けなさそうな場合でも、分類問題でラベル順にデータが並んでいる、一部のサンプル同士が同じグループに属している、などの場合は注意が必要です。これらの例については、稿を改め述べます。)
Train-Test split の場合と同じ様に、コードで見てみます。各サンプルが独立同分布(i.i.d.)に従っているとみなし、Foldの分割を、seed を変えてシャッフルしながら10回行い、クロスバリデーションで見積もられたRMSE値を出力します。
nfold = 5
# シャッフルのパターンを変えて実験繰り返し
for i in range(10):
kf = KFold(n_splits=nfold, random_state=i, shuffle=True)
rmse_cv_tr = []
rmse_cv_va = []
# クロスバリデーション
for idx_tr, idx_va in kf.split(x0):
x0_tr, x0_va = x0[idx_tr,:], x0[idx_va,:]
y0_tr, y0_va = y0[idx_tr,:], y0[idx_va,:]
model = LinearRegression()
model.fit(x0_tr, y0_tr)
y0_tr_pred = model.predict(x0_tr)
y0_va_pred = model.predict(x0_va)
rmse_cv_tr.append(np.sqrt(np.mean((y0_tr_pred - y0_tr)**2)))
rmse_cv_va.append(np.sqrt(np.mean((y0_va_pred - y0_va)**2)))
print("no split: {:.3f}, train: {:.3f} validation: {:.3f}".format(
rmse0,
np.array(rmse_cv_tr).mean(),
np.array(rmse_cv_va).mean())
)
no split: 5.645, train: 5.500 validation: 6.192
no split: 5.645, train: 5.523 validation: 5.987
no split: 5.645, train: 5.580 validation: 6.058
no split: 5.645, train: 5.543 validation: 6.492
no split: 5.645, train: 5.559 validation: 6.347
no split: 5.645, train: 5.600 validation: 5.759
no split: 5.645, train: 5.587 validation: 5.778
no split: 5.645, train: 5.545 validation: 5.913
no split: 5.645, train: 5.455 validation: 6.660
no split: 5.645, train: 5.503 validation: 6.230
validation の結果を見ると値の散らばりが少なくなっていることがわかります(複数回試行し、平均を取っているので当たり前ですが)。
クロスバリデーションによる(ハイパー)パラメータ探索#
複数のモデルを比較したり、モデルに予め与えなければならないパラメータ(ハイパーパラメータ)を変化させて実験することで最も精度の高い(誤差の小さい)モデルを得たい場合、最初の例のように「データセット0」すべてを使ってモデルの学習と評価を実行してしまうと、モデルが複雑になればなるほどtraining data に過剰に適合してしまい、未知データについての精度が低下するという問題が知られています(Over fitting: 過剰適合)。
クロスバリデーションは、このような場合に過剰適合を避けながら、モデルの精度を比較したり、最適なハイパーパラメータを探索したりする目的でよく使われています。
ハイパーパラメータを探索する場合に気をつけなければならないことがあります。見つけられた最適なパラメータはクロスバリデーションに使ったデータと過剰に適合してしまっている可能性がある、ということです。したがって、最適なパラメータを探索した上で、未知データに対する評価指標を見積るためには、クロスバリデーションに使われなかったサンプルを用いて評価する必要があります。手順は、以下の通りTrain-Test split とクロスバリデーションの組み合わせで行います。
Train-Test Split で、最終評価用のデータを取っておく。(Hold-out と呼ばれる)
Trainingデータを用いてクロスバリデーションを行いながらハイパーパラメータの探索(最も良い評価値のパラメータを探す)をおこなう。
探索されたハイパーパラメータをもちいてTrainingデータ全体を用いてモデルを学習し、Testセットで最終的な評価値を求める。
詳細については、たとえば、scikit-learnのドキュメントサイトなども参考になると思います。
クロスバリデーションによるハイパーパラメータ探索の例#
ここでは例として、以下のように説明変数を0乗からd乗したものまでをさらに説明変数として加えた重回帰モデルを考えてみます(0乗の係数は切片)。
次数が上がれば上がるほど訓練データに過剰にフィットします。このような条件の下、未知データに対して最も小さな RMSE を得られそうな次数 d が興味の対象となります。
以下のコードでは、上記と同じbostonデータを用います。Trainingデータとして20サンプル、Hold outデータとして、10サンプルを抽出して実験をします。
m = 12 # LSTAT の列番号
#Training
ntr = 30 # 20サンプル
x0 = X[:ntr,[m]]
y0 = Y[:ntr,:]
# Hold Out
nts = 15 # 10サンプル
x1 = X[ntr:ntr+nts, [m]]
y1 = Y[ntr:ntr+nts, :]
rmse_tr = [] # training での評価結果
rmse_va = [] # validation data での評価結果
rmse_ts = [] # test dataでの評価結果
ndim = 4
dims = [x+1 for x in range(ndim)]
for i in range(ndim):
poly = PolynomialFeatures(i+1)
xp0 = poly.fit_transform(x0)
kf = KFold(n_splits=nfold)
rmse_cv_tr = []
rmse_cv_va = []
for idx_tr, idx_va in kf.split(xp0):
xp0_tr, xp0_va = xp0[idx_tr,:], xp0[idx_va,:]
y0_tr, y0_va = y0[idx_tr,:], y0[idx_va,:]
model = LinearRegression()
model.fit(xp0_tr, y0_tr)
y0_tr_pred = model.predict(xp0_tr)
y0_va_pred = model.predict(xp0_va)
rmse_cv_tr.append(np.sqrt(np.mean((y0_tr_pred - y0_tr)**2)))
rmse_cv_va.append(np.sqrt(np.mean((y0_va_pred - y0_va)**2)))
#rmse_tr.append(np.array(rmse_cv_tr).mean())
rmse_va.append(np.array(rmse_cv_va).mean())
# Hold Out Evaluation
xp1 = poly.fit_transform(x1)
model0 = LinearRegression()
model0.fit(xp0, y0)
y0_pred = model0.predict(xp0)
rmse_tr.append(np.sqrt(np.mean((y0_pred - y0)**2)))
y1_pred = model0.predict(xp1)
rmse_ts.append(np.sqrt(np.mean((y1_pred - y1)**2)))
plt.plot(dims, rmse_tr, marker='x')
plt.plot(dims, rmse_va, marker='^')
plt.plot(dims, rmse_ts, marker='o')
plt.xticks(dims, dims)
plt.legend(['train', 'cv', 'test(hold out)'])
plt.xlabel("d")
plt.ylabel("RMSE")
plt.show()
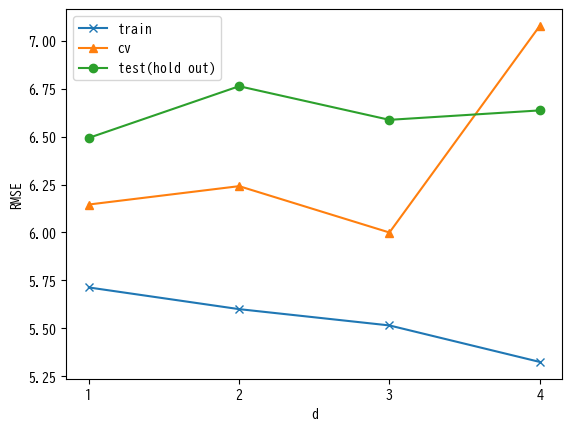
上の図は、横軸が次数d、縦軸がRMSEを表しています。訓練データすべてを使って学習した場合(train)は、次数が上がれば上がるほどRMSEが小さくなっています。cv はクロスバリデーションによる RMSE値を表しており、d=3の時に最適となっていて、d=4では急激に悪化しています。しかし、Hold outデータでの結果はクロスバリデーションの結果と一致しません。また傾向も同じになるとは限りません。この様に、学習にもクロスバリデーションによるパラメータ探索でも使われなかったデータ(すなわちHold outデータ)での評価がとても重要です。
時系列データの場合#
クロスバリデーションにおけるFoldへの分割の仕方について、データが独立同分布で生成されていると考えられるときには、ランダムに行えばよかったのですが、そうでない場合は注意が必要です。
経済時系列やプラントの時系列データは、典型的には過去の時刻と現在の時刻が関係しあっています。例えば、プラントデータにおいて、ランダムにシャッフルしてクロスバリデーションのデータセットを作った場合、関係しあっている(ときにはほとんど同じ値)2つの時刻のサンプルが学習とテストに分かれてしまうということが起きます。
通常の K-Fold クロスバリデーションを適用してみる#
時系列データの場合、どのようなことが起こるか、プラントデータの回帰の例でクロスバリデーションを行ってみましょう。ここでは、ハイパーパラメータを1つもつ、Lassoという重回帰分析の一種を使って実験します。Lassoは係数の絶対値の大きさをコントロールするためのハイパーパラメータがあり、sklearn.linear_model.Lasso() 関数では alpha オプションでこれを指定できます。今回は alpha だけを変化させてクロスバリデーションを行うことで最適な値を求めることを考えます。
プラントデータは1日分のシミュレーションデータで、91カラム(センサーなど)で構成されています。 ここでは、「気化器圧力_PV」カラムを目的変数、下のコードのsource_columnsに記されている28カラムを説明変数とします。
ここでは、28カラム分の変数を用いて、20秒後の「気化器圧力_PV」を予測するという問題を取り扱うことにします。つまり、各時刻の28カラム分の値を説明変数、その20秒後の「気化器圧力_PV」カラムの値を目的変数とした回帰モデルをLassoを用いて学習し、さまざまな alpha の値により評価します。
各カラムのデータは値のスケールをあわせるために、回帰モデルの学習をする前に、訓練データの平均と標準偏差を用いて正規化(標準化とも言います)します(具体的な内容については、「正規化」を参照してください)。
18時までのデータを学習・検証に使い、18時以降のデータを Hold out としてテスト用においておきます。
クロスバリデーションは18時までのデータに適用することとなります。まず、通常のK-Foldクロスバリデーションを以下の2つの分割方法で実施します。
サンプルの時間方向の順番をシャッフルする
シャッフルしない
# まずデータ読み込み
import pandas as pd
import numpy as np
fname = '../data/2020413.csv'
df = pd.read_csv(fname, index_col=0, parse_dates=True, encoding='cp932')
split_loc = df.index.get_loc('2020-04-13 18:00:00')
# 目的変数カラム
target_column = '気化器圧力_PV'
# 説明変数カラム
source_columns = [
'気化器圧力_MV',
'気化器温度_PV',
'気化器ヒータ出口温度_SV',
'熱交換器出口温度(リサイクルガス)_PV',
'セパレータ液面レベル_PV',
'セパレータ液体排出量_MV',
'セパレータ液体温度_PV',
'セパレータ外殻温度_MV',
'コンプレッサーヒーター熱量_MV',
'リサイクルガス圧力_PV',
'アブソーバ還流温度_PV',
'アブソーバスクラブ温度_PV',
'リサイクルガス流量_PV',
'有機生成物流量_MV',
'有機生成物レベル_PV',
'デカンタ温度_PV',
'コンデンサ熱量_MV',
'蒸留塔第5トレイ温度_PV',
'蒸留塔リボイラー熱量_MV',
'HAcタンクレベル_PV',
'有機生成物組成(H2O)_PV',
'排出ガス流量_MV',
'反応器流入組成(O2)_SV',
'原材料O2供給量_MV',
'反応器流入組成(C2H6)_PV',
'反応器流入組成(H2O)_PV',
'反応器流入組成(HAc)_PV',
'アブソーバ還流流量_MV (Fixed)'
]
# Training
Ytr = df[[target_column]].iloc[:split_loc].values
Xtr = df[source_columns].iloc[:split_loc].values
print("Training")
display(df[[target_column]+source_columns].iloc[:split_loc].head())
# Test (Hold out)
Yts = df[[target_column]].iloc[split_loc:].values
Xts = df[source_columns].iloc[split_loc:].values
print("Test")
display(df[[target_column]+source_columns].iloc[split_loc:].head())
Training
| 気化器圧力_PV | 気化器圧力_MV | 気化器温度_PV | 気化器ヒータ出口温度_SV | 熱交換器出口温度(リサイクルガス)_PV | セパレータ液面レベル_PV | セパレータ液体排出量_MV | セパレータ液体温度_PV | セパレータ外殻温度_MV | コンプレッサーヒーター熱量_MV | ... | 蒸留塔リボイラー熱量_MV | HAcタンクレベル_PV | 有機生成物組成(H2O)_PV | 排出ガス流量_MV | 反応器流入組成(O2)_SV | 原材料O2供給量_MV | 反応器流入組成(C2H6)_PV | 反応器流入組成(H2O)_PV | 反応器流入組成(HAc)_PV | アブソーバ還流流量_MV (Fixed) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2020-04-13 00:00:00 | 127.983294 | 18.728267 | 120.159558 | 150.0 | 98.056601 | 0.501359 | 2.754384 | 40.140573 | 36.001230 | 27192.421948 | ... | 67178.857911 | 0.500047 | 0.049956 | 0.003157 | 0.075 | 0.523430 | 0.214016 | 0.008524 | 0.109444 | 0.766 |
| 2020-04-13 00:00:01 | 128.262272 | 18.728267 | 120.072575 | 150.0 | 97.826309 | 0.499711 | 2.754384 | 40.419576 | 36.001230 | 27192.421948 | ... | 67178.857911 | 0.499237 | 0.049757 | 0.003157 | 0.075 | 0.523430 | 0.213945 | 0.008512 | 0.109441 | 0.766 |
| 2020-04-13 00:00:02 | 127.899077 | 19.079324 | 120.305327 | 150.0 | 97.816459 | 0.500240 | 2.751846 | 40.549778 | 36.701108 | 27886.016335 | ... | 60582.821045 | 0.500482 | 0.049916 | 0.003157 | 0.075 | 0.521454 | 0.215043 | 0.008541 | 0.109871 | 0.756 |
| 2020-04-13 00:00:03 | 127.622218 | 18.772228 | 120.219488 | 150.0 | 98.340920 | 0.500768 | 2.754157 | 40.426465 | 37.385460 | 28413.587346 | ... | 57729.202947 | 0.500308 | 0.049920 | 0.003157 | 0.075 | 0.531472 | 0.214126 | 0.008573 | 0.109775 | 0.746 |
| 2020-04-13 00:00:04 | 127.577243 | 18.605173 | 120.302267 | 150.0 | 98.096397 | 0.499504 | 2.759691 | 40.267525 | 37.636765 | 28710.322742 | ... | 54815.597151 | 0.499781 | 0.049769 | 0.003157 | 0.075 | 0.521279 | 0.214002 | 0.008547 | 0.109868 | 0.766 |
5 rows × 29 columns
Test
| 気化器圧力_PV | 気化器圧力_MV | 気化器温度_PV | 気化器ヒータ出口温度_SV | 熱交換器出口温度(リサイクルガス)_PV | セパレータ液面レベル_PV | セパレータ液体排出量_MV | セパレータ液体温度_PV | セパレータ外殻温度_MV | コンプレッサーヒーター熱量_MV | ... | 蒸留塔リボイラー熱量_MV | HAcタンクレベル_PV | 有機生成物組成(H2O)_PV | 排出ガス流量_MV | 反応器流入組成(O2)_SV | 原材料O2供給量_MV | 反応器流入組成(C2H6)_PV | 反応器流入組成(H2O)_PV | 反応器流入組成(HAc)_PV | アブソーバ還流流量_MV (Fixed) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2020-04-13 18:00:00 | 127.787558 | 18.581642 | 119.644542 | 147.692356 | 90.194396 | 0.499750 | 2.752314 | 39.390585 | 34.751373 | 27547.455299 | ... | 68896.580605 | 0.500063 | 0.049894 | 0.003379 | 0.078499 | 0.548254 | 0.218515 | 0.008489 | 0.107932 | 0.756 |
| 2020-04-13 18:00:01 | 127.604096 | 18.877220 | 119.707893 | 147.692356 | 90.241841 | 0.499823 | 2.750760 | 39.608400 | 34.385161 | 27531.268078 | ... | 68640.592955 | 0.500270 | 0.049899 | 0.003379 | 0.078499 | 0.534204 | 0.218387 | 0.008506 | 0.108369 | 0.756 |
| 2020-04-13 18:00:02 | 127.304774 | 18.682857 | 119.609059 | 147.692356 | 90.192856 | 0.498844 | 2.750275 | 39.338595 | 34.503502 | 27538.239522 | ... | 67908.723318 | 0.500036 | 0.049848 | 0.003379 | 0.078499 | 0.546499 | 0.218552 | 0.008506 | 0.108000 | 0.756 |
| 2020-04-13 18:00:03 | 127.706690 | 18.589099 | 119.612153 | 147.692356 | 90.389722 | 0.500178 | 2.742556 | 39.607139 | 34.131802 | 27505.928704 | ... | 69218.446545 | 0.499491 | 0.050039 | 0.003379 | 0.078499 | 0.538498 | 0.218532 | 0.008492 | 0.108316 | 0.766 |
| 2020-04-13 18:00:04 | 127.910510 | 18.739265 | 119.687702 | 147.692356 | 90.438064 | 0.500056 | 2.747491 | 39.631844 | 34.331030 | 27467.297762 | ... | 69999.052197 | 0.499101 | 0.049846 | 0.003379 | 0.078499 | 0.532526 | 0.218519 | 0.008482 | 0.107855 | 0.756 |
5 rows × 29 columns
from sklearn.linear_model import Lasso
# 実験条件
# Npred秒後の予測
Npred = 20 # 秒
# ハイパーパラメータのリスト
alphas = [0.1, 0.01, 0.001, 0.0001, 0.00001]
# 実験結果リスト
rmse_tr = [] # training dataでの評価結果
rmse_cv = [] # cross validationでの評価結果
rmse_cv2 = [] # cross validation の評価結果(シャッフルなし)
rmse_ts = [] # test dataでの評価結果
for a in alphas:
#
# 1. シャフルありの K-Fold クロスバリデーション
#
kf = KFold(n_splits=nfold, random_state=100, shuffle=True)
rmse_cv_tr = []
rmse_cv_va = []
# シャッフル用に目的変数の行をシフトして説明変数と目的変数の各行を対応させたものを用意
Xtr_sh = Xtr[:-Npred, :]
Ytr_sh = Ytr[Npred:]
# Fold ごとの計算
for idx_tr, idx_va in kf.split(Xtr_sh):
Xtrtr, Xtrva = Xtr_sh[idx_tr,:], Xtr_sh[idx_va,:]
Ytrtr, Ytrva = Ytr_sh[idx_tr], Ytr_sh[idx_va]
# 正規化
scalerX = StandardScaler()
scalerY = StandardScaler()
Xtrtr_norm = scalerX.fit_transform(Xtrtr)
Ytrtr_norm = scalerY.fit_transform(Ytrtr)
Xtrva_norm = scalerX.transform(Xtrva)
Ytrva_norm = scalerY.transform(Ytrva)
# 回帰モデルの学習
model = Lasso(alpha = a)
model.fit(Xtrtr_norm, Ytrtr_norm)
# 回帰モデルによる予測と、正規化の逆変換による元の目的変数の元のスケールへの変換
Ypred_trva = scalerY.inverse_transform(model.predict(Xtrva_norm).reshape(-1, 1))
# RMSEの計算
rmse_cv_va.append(np.sqrt(np.mean((Ypred_trva - Ytrva)**2)))
# RMSEの平均値を記録
rmse_cv.append(np.array(rmse_cv_va).mean())
#
# 2. シャッフルなしのクロスバリデーション
#
kf = KFold(n_splits=nfold, shuffle=False)
rmse_cv_tr = []
rmse_cv_va = []
# Fold ごとの計算
for idx_tr, idx_va in kf.split(Xtr):
# Npred 秒後予測を行うために、目的変数の行をシフトして説明変数と目的変数の各行を対応させる
Xtrtr, Xtrva = Xtr[idx_tr,:], Xtr[idx_va,:]
Xtrtr, Xtrva = Xtrtr[:-Npred, :], Xtrva[:-Npred, :]
Ytrtr, Ytrva = Ytr[idx_tr], Ytr[idx_va]
Ytrtr, Ytrva = Ytrtr[Npred:], Ytrva[Npred:]
# 正規化
scalerX = StandardScaler()
scalerY = StandardScaler()
Xtrtr_norm = scalerX.fit_transform(Xtrtr)
Ytrtr_norm = scalerY.fit_transform(Ytrtr)
Xtrva_norm = scalerX.transform(Xtrva)
Ytrva_norm = scalerY.transform(Ytrva)
# 回帰モデルの学習
model = Lasso(alpha = a)
model.fit(Xtrtr_norm, Ytrtr_norm)
# 回帰モデルによる予測と、正規化の逆変換による元の目的変数の元のスケールへの変換
Ypred_trva = scalerY.inverse_transform(model.predict(Xtrva_norm).reshape(-1, 1))
# RMSEの計算
rmse_cv_va.append(np.sqrt(np.mean((Ypred_trva - Ytrva)**2)))
# RMSEの平均値を記録
rmse_cv2.append(np.array(rmse_cv_va).mean())
#
# 3. Hold out データでの評価
#
# Npred 秒後予測を行うために、目的変数の行をシフトして説明変数と目的変数の各行を対応させる
Xtr_ho, Xts_ho= Xtr[:-Npred, :], Xts[:-Npred, :]
Ytr_ho, Yts_ho = Ytr[Npred:], Yts[Npred:]
# 正規化
scalerX = StandardScaler()
scalerY = StandardScaler()
Xtr_norm = scalerX.fit_transform(Xtr_ho)
Ytr_norm = scalerY.fit_transform(Ytr_ho)
Xts_norm = scalerX.transform(Xts_ho)
Yts_norm = scalerY.transform(Yts_ho)
# 回帰モデルの学習
model = Lasso(alpha = a)
model.fit(Xtr_norm, Ytr_norm)
Ypred_tr = scalerY.inverse_transform(model.predict(Xtr_norm).reshape(-1, 1))
Ypred_ts = scalerY.inverse_transform(model.predict(Xts_norm).reshape(-1, 1))
#RMSEの計算
rmse_tr.append(np.sqrt(np.mean((Ypred_tr - Ytr_ho)**2)))
rmse_ts.append(np.sqrt(np.mean((Ypred_ts - Yts_ho)**2)))
cmap = plt.get_cmap("tab10") # 色を指定するためのオブジェクト
plt.plot(rmse_tr, marker='x', color=cmap(0))
plt.plot(rmse_cv, marker='+', color=cmap(4))
plt.plot(rmse_cv2, marker='v', color=cmap(5))
plt.plot(rmse_ts, marker='s', color=cmap(3))
plt.legend(['train', 'ordinary k-fold cv (shuffle)', 'ordinary k-fold cv(no shuffle)', 'test(hold out)'])
plt.xticks([x for x in range(len(alphas))], [str(x) for x in alphas])
plt.xlabel("alpha")
plt.ylabel("RMSE")
plt.title("ハイパーパラメータ alpha と RMSEの関係の比較\n(Train, K-Foldクロスバリデーション[シャッフル有り/なし], Test)")
plt.show()
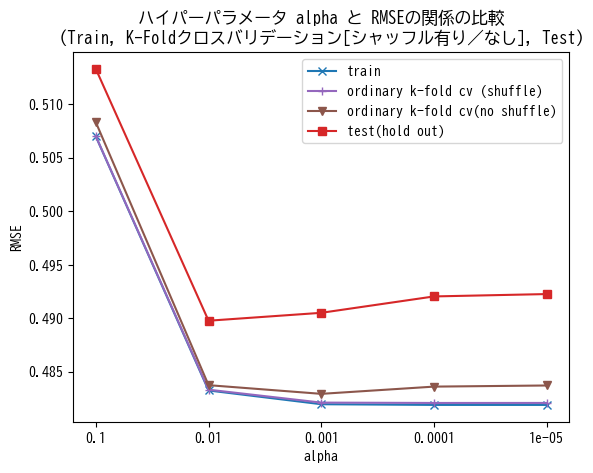
クロスバリデーションを用いたハイパーパラメータの探索は、各パラメータ(ここでは alpha )でクロスバリデーションを行い、指標(今回はRMSE)の平均値を計算します。そしてその中で最も良い(RMSEの値が小さい)パラメータ値を採用し、最後にHold outデータにて評価を実施する、という手順で行います。ここでは比較のために、Hold outデータ、および全訓練データで学習して同じ訓練データで評価した場合においてもさまざまな alpha を用いた場合のRMSE値を計算し、グラフ上に描画しています(それぞれ赤色と青色)。
上記の結果を見ると、シャッフルを行う通常のK-Foldクロスバリデーション(薄紫色)では、訓練データ(青色)と重なり、Hold out データと比べ高い精度(低RMSE値)を示しています。これは、隣り合う強く関連しているサンプルが学習とテストに分かれて入ってしまっているためと考えられます。シャッフルがないK-Foldクロスバリデーション(茶色)でも Hold out データよりも低いRMSE値となっています。
また、すべての場合において、alpha を0.1から0.01に減少させると大きく精度が改善し、それ以降は横ばいになるという傾向が見られます。Hold outデータでは、alpha=0.01のときがベストで、K-Fold(シャッフルなし)では alpha=0.001 のときがベストとなっています。
この結果や本稿で述べてきた評価方法の仕組みを考慮し、運用時の精度の見積りや、ハイパーパラメータの探索の目的で K-Fold クロスバリデーションの利用を検討する場合は、少なくともシャッフルの適用は避けるべきです。 またシャッフルなしの場合も、過大な評価となってしまう場合があることは留意し、次節以降で述べる方法などを検討することを推奨します。
時系列クロスバリデーション#
前節で述べたように、一般的に独立同分布が仮定できない時系列データにおけるクロスバリデーションでシャッフルを行ってしまうと、未知データに対する精度がわからなくなってしまいます。このような場合、関連性の高いことが分かっているグループに分けて、グループ内のサンプルが学習とテストで分かれないようにしてFoldに分割する方法が使われたりします(Group K-Fold と呼ばれる場合もあります)。上記シャッフルなしの場合も、連続する時間帯をグループとみなして Fold を作っていると考えれば同様の手法であると考えることが出来ます。
例えば、scikit-learn には、TimeSeriesSplit という関数があります。上記シャッフルなしの場合と少し違うのが、テストデータより未来のデータは訓練データから除く 点です。したがって、「実験1」は存在せず、「実験2」 〜 「実験5」を行うことになります。実際、実時間のシステムの運用において回帰モデルを利用する際には、未来のデータを用いての学習はできませんので、現実に即した評価方法と言えるでしょう。(どのFoldをテストに使うかで訓練データのサンプル数が変わってしまうという問題があります。)
from sklearn.model_selection import TimeSeriesSplit
rmse_cvts = [] # 時系列cross validationでの評価結果
for a in alphas:
kf_ts = TimeSeriesSplit(n_splits=nfold)
rmse_cv_tr = []
rmse_cv_va = []
# Fold ごとの計算
for idx_tr, idx_va in kf_ts.split(Xtr):
Xtrtr, Xtrva = Xtr[idx_tr,:], Xtr[idx_va,:]
Xtrtr, Xtrva = Xtrtr[:-Npred, :], Xtrva[:-Npred, :]
Ytrtr, Ytrva = Ytr[idx_tr], Ytr[idx_va]
Ytrtr, Ytrva = Ytrtr[Npred:], Ytrva[Npred:]
# 正規化
scalerX = StandardScaler()
scalerY = StandardScaler()
Xtrtr_norm = scalerX.fit_transform(Xtrtr)
Ytrtr_norm = scalerY.fit_transform(Ytrtr)
Xtrva_norm = scalerX.transform(Xtrva)
Ytrva_norm = scalerY.transform(Ytrva)
# 回帰モデルの学習
model = Lasso(alpha = a)
model.fit(Xtrtr_norm, Ytrtr_norm)
# 回帰モデルによる予測と、正規化の逆変換による元の目的変数の元のスケールへの変換
Ypred_trva = scalerY.inverse_transform(model.predict(Xtrva_norm).reshape(-1, 1))
# RMSEの計算
rmse_cv_va.append(np.sqrt(np.mean((Ypred_trva - Ytrva)**2)))
rmse_cvts.append(np.array(rmse_cv_va).mean())
plt.plot(rmse_tr, marker='x', color=cmap(0))
plt.plot(rmse_cvts, marker='^', color=cmap(1))
plt.plot(rmse_cv2, marker='v', color=cmap(5))
plt.plot(rmse_ts, marker='s', color=cmap(3))
plt.legend(['train', 'time series cv', 'ordinary cv(no shuffle)', 'test(hold out)'])
plt.xticks([x for x in range(len(alphas))], [str(x) for x in alphas])
plt.xlabel("alpha")
plt.ylabel("RMSE")
plt.title("ハイパーパラメータ alpha と RMSEの関係の比較\n(Train, クロスバリデーション[時系列/K-Foldシャッフルなし], Test)")
plt.show()

time series cv を見ると、alpha を0.1から0.01に変化させたとき大きく改善するところまでは、通常の K-Fold のシャッフルなし(cv(no shuffle)) と同じ傾向ですが、その後 alpha をさらに小さくするとRMSEが増加するという傾向が見られました。Hold outでも若干この傾向はあるものの、やや極端に出ているようです。全体的にはK-Fold(シャッフルなし)よりも大きなRMSE値となっており、 alpha=0.00001 ではHold Out よりも大きくなっています。いろいろな理由が考えられると思いますが、時間的に状態変化するデータであること(各Foldでテストデータに対応する状態が訓練データに含まれていないことがある)や、クロスバリデーションでの各試行の訓練データ数が少ない、などが考えられます。
最適な alpha の値を探索する、という観点では、この例ではHold out と同様、 alpha = 0.01 が得られています。
Walk forward validation#
時系列クロスバリデーションでは、Foldごとに訓練データのサンプル数が変わりますが、応用の場面ではシステムの要請や経年変化の影響を軽減するなどの目的で、直近の一定期間の移動窓で切り出して訓練データを作るような場合があります。このような場合のクロスバリデーションとして、Walk forward validation があります(下図参照)。
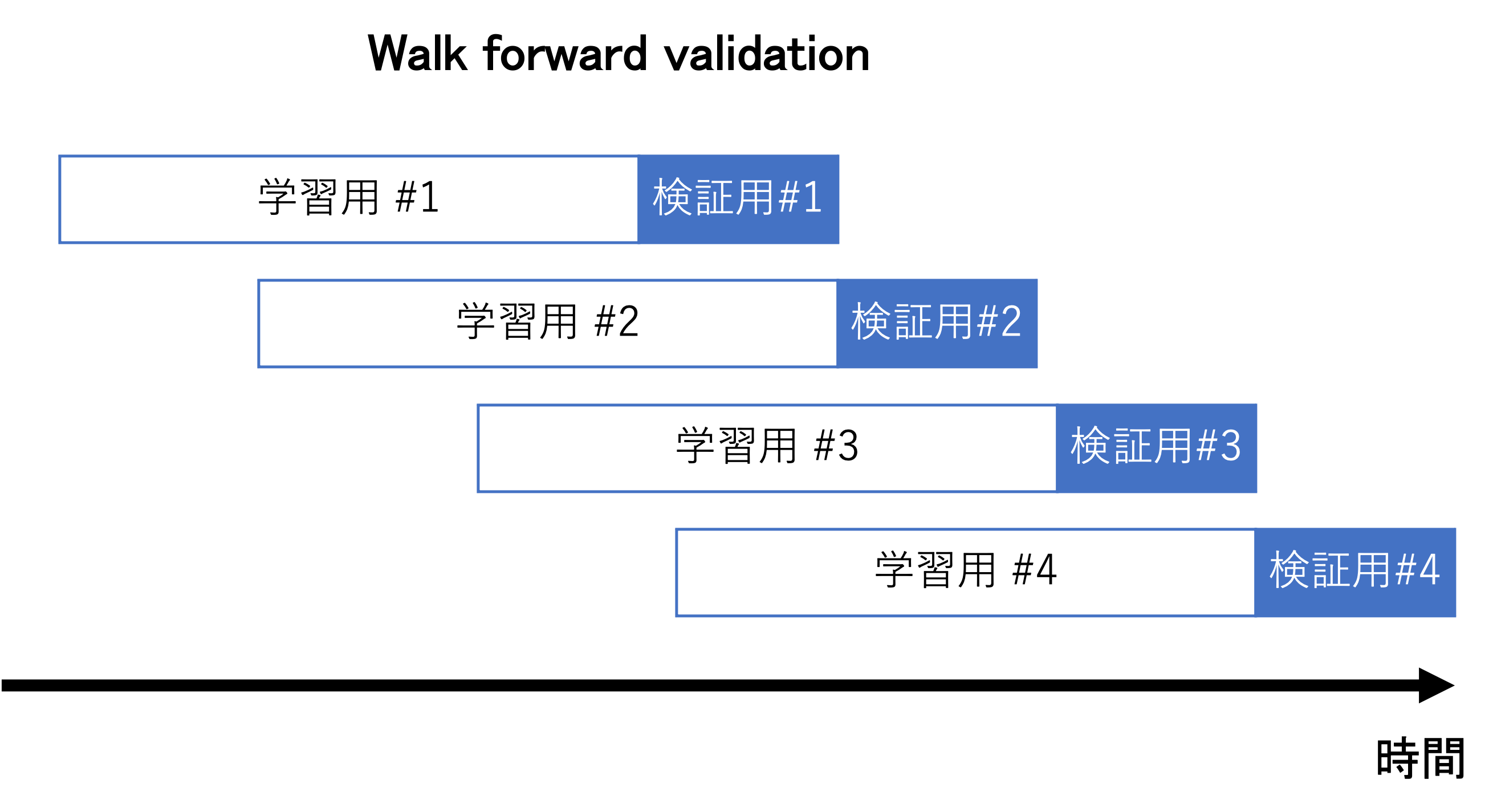
時系列クロスバリデーションにおいて、バリデーションデータの直前の固定長のデータを訓練データとして使う、という修正を加えたものとなります。主に、株の自動トレーディングアルゴリズムの評価や、経年変化するプラントのソフトセンサーを用いた予測システムの評価 [泉谷2017] などに使われているようです。
以下の例は、上記と同じデータセットに対して Walk forward validation を適用したものです。簡略化のために、訓練データとバリデーションデータは同じサンプル数にしました。つまりデータを時間方向に K+1 等分(K+1 Fold)し、連続する2つのFoldを学習とバリデーションに使う、というものです。本来は学習サンプル確保のため上図のようにオーバーラップして十分な学習サンプル数をとることが望ましいです。
rmse_cvwf = [] # walk forward validationの評価結果
# ハイパーパラメータのリスト
ndim = 4
dims = [x+1 for x in range(ndim)]
nrow = Xtr.shape[0]
for a in alphas:
# Walk forward validation
nsplit = nfold + 1
l, rem = divmod(nrow, nsplit)
# 各foldの長さ
len_fold = [l+1 if x<rem else l for x in range(nsplit)]
# 各foldの開始および終了indexをリスト化
ens = list(np.cumsum(len_fold))
sts = [0] + ens[:-1]
idxs = list(zip(sts, ens))
# Walk forward validation: Fold ごとの計算
for k in range(nfold):
Xtrtr = Xtr[idxs[k][0]:idxs[k][1], :]
Ytrtr = Ytr[idxs[k][0]:idxs[k][1]]
Xtrva = Xtr[idxs[k+1][0]:idxs[k+1][1], :]
Ytrva = Ytr[idxs[k+1][0]:idxs[k+1][1]]
# Npred 秒後予測を実行するために、目的変数の行をシフトして説明変数と目的変数の各行を対応させる
Xtrtr, Xtrva = Xtrtr[:-Npred, :], Xtrva[:-Npred, :]
Ytrtr, Ytrva = Ytrtr[Npred:], Ytrva[Npred:]
# 正規化
scalerX = StandardScaler()
scalerY = StandardScaler()
Xtrtr_norm = scalerX.fit_transform(Xtrtr)
Ytrtr_norm = scalerY.fit_transform(Ytrtr)
Xtrva_norm = scalerX.transform(Xtrva)
Ytrva_norm = scalerY.transform(Ytrva)
# 回帰モデルの学習
model = Lasso(alpha = a)
model.fit(Xtrtr_norm, Ytrtr_norm)
# 回帰モデルによる予測と、正規化の逆変換による元の目的変数の元のスケールへの変換
Ypred_trva = scalerY.inverse_transform(model.predict(Xtrva_norm).reshape(-1, 1))
# RMSE の計算
rmse_cv_va.append(np.sqrt(np.mean((Ypred_trva - Ytrva)**2)))
# RMSEの平均値を記録
rmse_cvwf.append(np.array(rmse_cv_va).mean())
plt.plot(rmse_tr, marker='x', color=cmap(0))
plt.plot(rmse_cvts, marker='^', color=cmap(1))
plt.plot(rmse_cvwf, marker='o', color=cmap(2))
plt.plot(rmse_ts, marker='s', color=cmap(3))
plt.legend(['train', 'time series cv', 'walk forward cv', 'test(hold out)'])
plt.xticks([x for x in range(len(alphas))], [str(x) for x in alphas])
plt.xlabel("alpha")
plt.ylabel("RMSE")
plt.title("ハイパーパラメータ alpha と RMSEの関係の比較\n(Train, クロスバリデーション[時系列/Walk forward], Test)")
plt.show()
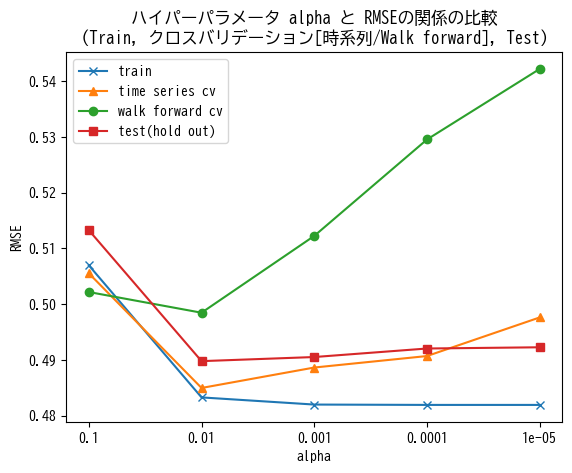
結果を見ると、時系列クロスバリデーションと類似した傾向を見て取ることができますが、 alpha の値を小さくしたときのRMSE値の増大が顕著になっております。各Foldにおける学習に使うデータのサンプル数が時系列クロスバリデーションに比べさらに減少することや、訓練データのカバレッジ(経時変化する系において、短い時間のみしかモデルの学習に使っていない)などの問題が考えられます。最適な alpha の値は、時系列クロスバリデーションと同様、0.01となりました。
時系列クロスバリデーションとWalk forward validation のどちらをとるべきかについては、分析対象の性質によると思われますが、理論的な背景は必ずしも明確になっていません。系の経時的な変化が常にあり、直近のデータだけで学習したモデルを用いて予測を実行する運用を想定する場合には、訓練データ数や訓練データとテストデータの時間的関係などを揃えられるという意味において、Walk forward validation を用いた評価に優位性があると考えられます。
気をつける点(Data Leakage)#
独立同分布でない時系列データに対するシャッフル付きのK-Foldクロスバリデーションの例の様に、せっかくクロスバリデーションとHold out を用いて実験したとしても、出てきた結果に意味がなくなってしまう場合があるので、注意が必要です。
上記のようなケースは、テストまたはバリデーションデータの情報が訓練データの値に影響を与えている(独立でない)ような場合に多く発生します。最近では、テストデータの情報が訓練データに漏れてしまうというニュアンスで、Data Leakage または単に Leakage と呼ばれることがあります。詳しくは、こちらのKaggleの記事などを参照してください。
Data Leakage で見逃しやすいケースとして、データの前処理、標準化などを行う時に、Training とバリデーションや Testのデータを混ぜてしまう、という点です。それらの処理は、Train と Test とに分けた後、さらにクロスバリデーションの各実験においてはモデルの学習とバリデーションのデータに分割した後で、別々に行うことが肝要です。
小括#
回帰分析を用いる場合、未知データでの性能を手持ちのデータだけから見積る試みとしてのクロスバリデーションを紹介しました。世の中はサンプルに独立同分布を仮定して議論されている場合が多いですが、時系列データの場合は隣接する時刻など、サンプル間の依存性が強く、フェアな評価が難しくなっているというケースがあります。また、あまり需要がないのか、教科書、論文などの記述も十分になされていない場合がほとんどです。
本稿では、scikit-learn などのツールのドキュメントなどで関連する情報を集めて時系列データに対する回帰分析の評価を中心に、(長めになりましたが)コードを含めて記述しました。
現実の応用場面ではどこにどの処理を入れるかなど悩むこともあるかとおもいますが、システム化して運用したときに、とくに未来のデータが得られていないリアルタイム処理を想定した場合、計算速度は抜きにして、同じ条件の実験ができるかどうかというのが1つの基準になるのではないかと思います。
参考文献#
[泉谷2017] 泉谷知範, et al. "ニューラルネットワークを用いたガスプラントの品質予測." 人工知能学会全国大会論文集 第 31 回全国大会 (2017). 一般社団法人 人工知能学会, 2017.

