Just-In-Time モデリング

今回はJust-In-Timeモデリング(JIT)と呼ばれるフレームワークをご紹介します。

サマリー

• プラントソフトセンサーなどで非線形システムのモデリングに使われる手法

• 近傍探索を利用し、大域的には非線形となる現象を局所的に線形のモデルで表現。非定常性や分布シフトにも対応

• 入力が与えられるたびに近傍データで学習を行い、学習されたモデルに改めて入力を行い出力を作成

背景

これまで紹介した(時系列)分析の手法の多くは、データの独立同分布(i.i.d.)や定常性を仮定していたり、変数間の関係性に線形性を仮定していました。しかし、現実のデータではこういった仮定は崩れている場合が多いです。

例えばプラントシステムなどは、対象とする化学製品の化学反応に起因する変数間の非線形な関係を含んでいたり、外気温の変化に起因する季節性や設備の経年劣化、定期修理などによる分布シフトがしばしば発生します。このような条件下で例えば基本的な回帰モデルで解説された線形手法などを適用した場合、

• 非線形性を捉えきれず精度が十分出ない

• 学習後モデルを運用していると分布シフトにより精度が段々下がっていく

といった問題が発生します。これらの問題を可視化したのが以下の図です。

非線形性や非定常性に関する課題

この図は、冬期に500トンの目標生産量で運転されていたプラントのデータを用いてモデルを、夏期に目標精算量100トンで運転している同じプラントのデータに適用した場合、出力された予測値にズレが生じる例を示しています。原因として、プラントの老朽化などの経年変化や運転条件の変化により、データの分布が変化したり（分布シフトとも呼ばれる）、データがトレンドや季節性を含んだりすることなどが考えられます。また、システムそのものが複雑な非線形性を持ち、線形手法での解析が難しい場合もありあます。

Just-In-Timeモデリング

アルゴリズムの概要

こうした問題に対し、ニューラルネットワーク(NN)などの非線形モデルや非定常性を考慮したモデルなど、強力な単一のモデルを用いて対応する手もありますが、今回紹介するJust-In-Timeモデルでは比較的単純なモデルに対してメタ的な学習フレームワークを適用し解決します。

Just-In-Timeモデルの基本的なアイデアは以下になります。

• 大域的に非線形なモデルも、入力点の付近で局所的に見れば線形に近似できる(テイラー近似)

• 非定常な分布シフトやクラスタがあった場合も、付近のデータだけを取ってくればその範囲のデータでは定常と見做せる

以上の期待から、JITでは非線形性と非定常性を持つデータに対してロバストにするために、入力値の近傍のデータだけを利用してモデリングを行います。 具体的には、入力が与えられる度に入力値のK近傍データ(とその出力値)を学習データとしてモデルの学習を行い、その学習済みモデルを使って改めて入力値から出力値を計算します。 この意味でJITは学習を後回しにする Lazy (怠惰な) Learning などと呼ばれたり、必要に応じて予測を行うOn-Demand予測などとも呼ばれます。

この方法は、運用時などにデータが与えられる度に学習を行いモデルを改善していくいわゆる逐次学習 (Online Learning)や、次々にタスクやデータが追加される状況で元のタスクの精度を損なわず新しいタスクを学習する、継続学習 (Continual Learning)、学習時のソースドメインからテスト時のターゲットドメインへの汎化を考えるドメイン適応、などの分野との関連も考えられます。

JITの注意点

JITは入力の度に学習を行うため、推論時に実行速度が遅くなりやすい欠点があります。 実システム導入を考えると、現実的にはモデルの制約として高速な学習が可能な比較的軽量なモデルを使う必要があります。 基本的には、局所モデリングにより、線形モデルといった(テイラー近似の意味で)低次のモデルの利用が推奨されます。

近傍はなんらかの距離尺度に基づいて計算されます。例えば多変量時系列データに対して、遅れ変数(詳しくは時間窓切り出し処理参照)を含むベクトル \(\boldsymbol{x}^{(t)} \, (t=1,2,...)\)によるデータベースを構成し、ユークリッド距離やマハラノビス距離を取ることができます。

入力値の近傍に十分なデータ密度が確保できるような多量のデータに対してJITを適用することを前提としているため、JITの計算量のボトルネックはこの近傍探索部分になります。一般に近傍探索についてはよく研究がされており、既存の高速な近似アルゴリズムや、ライブラリを使った高速解法を使用するのがおすすめです。

また、高次元データに対する近傍探索は、最近傍点と最遠傍点との差が小さくなってしまうなど、いわゆる次元の呪いにより不安定になる傾向があるため、こちらも注意が必要です。

以上をまとめるとJITのアルゴリズムは以下のようになります。

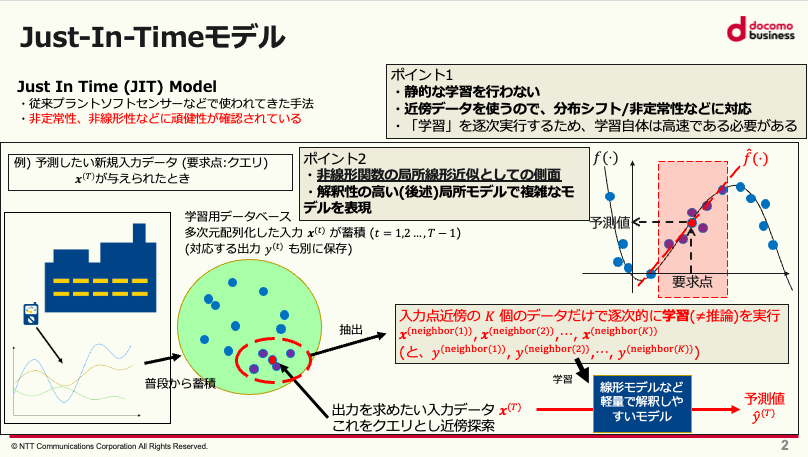
Just-In-Timeモデルの概念図

この図は、Just-In-Timeモデルのアルゴリズムの動きを可視化したものになります。まず、学習用のデータベースに普段からシステムのデータを蓄積しておきます。入力データが与えられた時、その入力を要求点(クエリ)としてデータベース上で近傍探索を行い、近傍データをK個抽出します。最後にその抽出されたデータを用いて基本的な回帰モデルで解説された手法など軽量で解釈しやすいモデルを用いて回帰を行います。

Just-In-Time モデルの実装

では、前述のJITのアルゴリズムを実装します。

実験高速化のため、先に近傍探索のみを独立して全時刻に対して実行し、その結果を得た上で各時刻の予測値を作成する手順を取ります。

したがって、今回実装するのは実際のシステム導入に使えるリアルタイム予測用ではなく、基本的には過去データに対する精度検証のバックテスト用コードになることに注意して下さい。

モジュールの構成要素は以下のようになっています。

• 近傍探索モジュール：各時刻において、それ以前の時刻からK近傍を探索し、探索された時刻のインデクスと距離を出力する。

• ベースとなるモデル(のラッパー)：sklearn likeなモデルなどで学習を実行し、具体的な推論値や、学習された重回帰係数と切片など、なんらかの学習結果を出力するラッパー

• 学習モジュール：近傍探索モジュールによって事前に探索されたK近傍のデータとベースとなるモデル(のラッパー)を用いて、各時刻で近傍データに対し学習を実行し、その結果を保存する。

近傍探索モジュール

先に、近傍探索部分を担当するコードを書きます。時間のかかる近傍探索処理を高速で実行するため、具体的な近傍探索部分はMeta社が公開している高速近傍探索ライブラリfaissを利用します。インストールに関してはこちらを参考下さい。

# cpu版のfaissをインストール
!conda install -c conda-forge faiss-cpu -y

Show code cell output Hide code cell output

Collecting package metadata (current_repodata.json): done
Solving environment: done


==> WARNING: A newer version of conda exists. <==
  current version: 4.11.0
  latest version: 25.1.0

Please update conda by running

    $ conda update -n base conda



# All requested packages already installed.

次に、近傍探索モジュールを読み込みます。コードが長いので折りたたんでおきます。

Show code cell content Hide code cell content

# NeighborSearch.py
# 近傍探索モジュール

# faissが未インストールの場合 scikit-learn NearestNeighborsを使用
from sklearn.neighbors import NearestNeighbors
import numpy as np

faiss_imported = False
try:
    import faiss

    faiss_imported = True
except ModuleNotFoundError as e:
    print("warning:")
    print(e)
    print(
        "warning: now you can't use faiss fast neighbor search methods such as 'faiss_KNN'. "
    )
    print("warning: you should use scikit-learn methods such as 'KNN', 'ERN'. ")
    print(
        "warning: if you want use fassis,  see https://github.com/facebookresearch/faiss/blob/main/INSTALL.md and install it."
    )
except:
    raise Exception("faiss import error")


class NeighborSearch:
    """JIT用の近傍探索部分モジュール。各時刻について、それより前の時刻の観測から近傍を選ぶ。

        Attributes
        ----------
        distance_records : np.ndaraay
            近傍探索結果。時間数 x 近傍数(k) の二次元配列。各近傍サンプルの距離が入っている。

        indices_records : np.ndarray
            近傍探索結果。時間数 x 近傍数(k) の二次元配列。各近傍サンプルのindexが入っている。

        Methods
        -------
        run(data)
            全時間に対して近傍探索を実行。

        Examples
        --------
        >>> data = np.array(
        ...     [
        ...         [0, 0, 1],
        ...         [0, 0, 2],
        ...         [0, 0, 3],
        ...         [0, 0, 4],
        ...         [0, 0, 5],
        ...         [1, 0, 6],
        ...         [1, 0, 7],
        ...         [1, 0, 8],
        ...         [1, 0, 9],
        ...     ]
    )
        >>> ns = NeighborSearch(k=3)
        >>> ns.run(data)
        ... (array([[-1.        , -1.        , -1.        ],
        ...         [-1.        , -1.        , -1.        ],
        ...         [-1.        , -1.        , -1.        ],
        ...         [ 1.        ,  2.        ,  3.        ],
        ...         [ 1.        ,  2.        ,  3.        ],
        ...         [ 1.41421356,  2.23606798,  3.16227766],
        ...         [ 1.        ,  2.23606798,  3.16227766],
        ...         [ 1.        ,  2.        ,  3.16227766],
        ...         [ 1.        ,  2.        ,  3.        ]]),
        ...  array([[-1, -1, -1],
        ...         [-1, -1, -1],
        ...         [-1, -1, -1],
        ...         [ 2,  1,  0],
        ...         [ 3,  2,  1],
        ...         [ 4,  3,  2],
        ...         [ 5,  4,  3],
        ...         [ 6,  5,  4],
        ...         [ 7,  6,  5]]))

    """

    def __init__(
        self,
        k: int,
        epsilon: float = None,
        metric: str = "Euqlid",
        method: str = "KNN",
        delta: float = 0.1,
        search_exculusion: int = 0,
        batch=5000,
        switch=0,
        reduction_dim=10,
    ):
        """探索用パラメータ設定を行う。
        KNNは近い順位にK個、ERNは距離epsion以内の近傍からランダムにK個。

        Parameters
        ----------
        k : int
            探索する近傍の数。KNNでもERNでも必須
        epsilon : float, optional
            探索近傍の半径。ERNで必須, by default None
        metric : str, optional
            距離指標。"Euqlid"、"Mahalanobis"、"PCA_Reduction" など , by default "Euqlid"
        method : str, optional
            近傍選択法。"KNN"、"ERN"、"faiss_KNN"、"faiss_approximate_KNN"が選択可, by default "KNN"
        delta : float, optional
            ERN時にサンプルがK個以下なら、K以上になるまでdeltaずつ半径を拡大する。, by default 0.1
        search_exculusion : int, optional
            検索除外期間。近傍探索から直近のsearch_exculusion個のサンプルは除外, by default 0
        batch : int, optional
            method="faiss_approximate_KNN" 選択時にバッチ処理を行う。batch個のサンプルが貯まるまで検索対象となるデータベースは更新されない, by default 5000
        switch : int, optional
            method="faiss_approximate_KNN" 選択時に、非近似版と近似版の探索アルゴリズムをスイッチするタイミング。少数データ時(10000オーダー以下)は非近似版が早い, by default 0
        reduction_dim : int, optional
            method="PCA_Reduction" 選択時に次元削減後の次元数, by default 10
        """

        # attributes
        self.data = None
        self.distances_records = None
        self.indices_records = None

        # setting
        self.k = k
        assert (
            self.k is not None
        ), "argument k is missing (must be given in KNN and ERN)!"

        self.epsilon = epsilon
        self.metric = metric

        self.method = method
        available_methods = [
            "KNN",
            "ERN",
            "faiss_KNN",
            "faiss_approximate_KNN",
        ]
        if not faiss_imported:
            available_methods = [i for i in available_methods if "faiss" not in i]

        assert method in available_methods, f"available_methods : {available_methods}"

        if method == "ERN":
            assert (
                self.epsilon is not None
            ), "argument epsilon is missing (must be given in ERN)!"

        self.delta = delta

        self.search_exculusion = search_exculusion

        self.batch = batch
        self.cache = 0
        self.index = None
        self.switch = switch

        self.reduction_dim = reduction_dim

    def run(self, data: np.ndarray):
        """近傍探索を実行。各時刻について、それより前の時刻の観測から近傍を選び、結果(距離とindex)を格納した二次元配列をそれぞれ返す。

        Parameters
        ----------
        data : np.ndarray
            時間数 x 特徴量数 の二次元配列。時刻tでdata[:t]が検索対象となるデータベース、data[t]がクエリとなる。

        Returns
        -------
        np.ndarray(float), np.ndarray(int)
            2つの返り値はどちらも 時間数 x 近傍数(k) の二次元配列。後者は、t行目に時刻tの検索でそれぞれ近い順にサンプルのindexをk個格納。前者がそれぞれの距離。値が出せないところは-1で初期化。
        """

        # 初期化
        self.distances_records = np.full(
            (data.shape[0], self.k), fill_value=-1.0, dtype=float
        )
        self.indices_records = np.full(
            (data.shape[0], self.k), fill_value=-1, dtype=int
        )

        # JITプロセス
        for i in range(len(data)):
            if i >= self.k + self.search_exculusion:
                X_query = data[i][np.newaxis, :]
                X_database = data[: i - self.search_exculusion]

                # 適当なメトリック用に写像
                # self.project(X_database,X_query,"Euqlid")みたいに書き直した方がいいかも
                if self.metric == "Euqlid":
                    pass
                elif self.metric == "Mahalanobis":
                    x_mean = np.mean(X_database, axis=0)
                    U, S, Vh = np.linalg.svd(X_database - x_mean, full_matrices=False)
                    if np.any(S < 1.0e-308):
                        eps = 1.0e-300
                        S = S + eps
                    # この行列Qによる写像後に距離を計算するのと等価になる
                    Q = np.sqrt(X_database.shape[0]) * np.diag(1 / S) @ Vh
                    X_database = X_database @ (Q.T)
                    X_query = X_query @ (Q.T)
                elif self.metric == "PCA_Reduction":
                    x_mean = np.mean(X_database, axis=0)
                    U, S, Vh = np.linalg.svd(X_database - x_mean, full_matrices=False)
                    if np.any(S < 1.0e-308):
                        eps = 1.0e-300
                        S = S + eps
                    # 特異値(固有値)の大きい順にself.reduction_dim個の固有ベクトルを取って写像
                    # 特異値もself.reduction_dim個だけ取って球状化
                    Q_reduced = (
                        np.sqrt(X_database.shape[0])
                        * np.diag(1 / S[: self.reduction_dim])
                        @ Vh[: self.reduction_dim]
                    )
                    X_database = X_database @ (Q_reduced.T)
                    X_query = X_query @ (Q_reduced.T)
                    assert Q_reduced.shape[0] == min(
                        self.reduction_dim, X_database.shape[0]
                    ), f"{Q_reduced.shape}"
                    assert X_database.shape[1] == min(
                        self.reduction_dim, X_database.shape[0]
                    ), f"{X_database.shape}"
                else:
                    raise Exception("use undefined metrics !")

                if self.method == "KNN":
                    distances, indices = self._knn(X_query, X_database)
                elif self.method == "ERN":
                    distances, indices = self._ern(X_query, X_database)
                elif self.method == "faiss_KNN":
                    distances, indices = self._faiss_knn(X_query, X_database)
                elif self.method == "faiss_approximate_KNN":
                    distances, indices = self._faiss_approximate_knn(
                        X_query, X_database
                    )
                else:
                    raise Exception("Neighbor Search Method Selection Error!")

                self.distances_records[i] = distances
                self.indices_records[i] = indices

        return self.distances_records, self.indices_records

    def _knn(self, X_query: np.ndarray, X_database: np.ndarray):

        self.nn = NearestNeighbors()
        self.nn.fit(X_database)
        distances, indices = self.nn.kneighbors(X_query, n_neighbors=self.k)

        return distances[0], indices[0]

    def _ern(self, X_query: np.ndarray, X_database: np.ndarray):

        self.nn = NearestNeighbors()
        self.nn.fit(X_database)

        neighbor_num = 0
        extention = 0.0
        while neighbor_num < self.k:
            distances, indices = self.nn.radius_neighbors(
                X_query, radius=self.epsilon + extention
            )
            assert type(indices[0]) == np.ndarray
            neighbor_num = indices[0].shape[0]
            extention += self.delta

        selected_sample = np.random.choice(range(neighbor_num), self.k, replace=False)

        assert indices[0][selected_sample].ndim == 1
        assert indices[0][selected_sample].shape[0] == self.k
        assert distances[0][selected_sample].ndim == 1
        assert distances[0][selected_sample].shape[0] == self.k

        distances = distances[0][selected_sample]
        indices = indices[0][selected_sample]

        distances, indices = self._sort_results(distances, indices)

        return distances, indices

    def _faiss_knn(self, X_query: np.ndarray, X_database: np.ndarray):
        index = faiss.IndexFlatL2(X_database.shape[1])
        index.add(X_database.astype(np.float32))
        square_distances, indices = index.search(X_query.astype(np.float32), self.k)

        return np.sqrt(square_distances[0]), indices[0]

    def _faiss_approximate_knn(self, X_query: np.ndarray, X_database: np.ndarray):
        if X_database.shape[0] < self.switch:
            distances, indices = self._faiss_knn(X_query, X_database)
        else:
            if self.cache <= 0:
                # 空間に均等に分布していると仮定すると
                # 大体(近傍数self.k)分の１ぐらいの分割数が良さそう？
                # (1クラスターへの所属サンプル数がk個になるので)
                # 2を下回らないように
                nlist = X_query.shape[0] // (2 * self.k) + 1
                quantizer = faiss.IndexFlatL2(X_database.shape[1])
                index = faiss.IndexIVFFlat(
                    quantizer, X_database.shape[1], nlist, faiss.METRIC_L2
                )
                # ボロノイ分割を学習
                index.train(X_database.astype(np.float32))
                self.index = index

                self.index.add(X_database.astype(np.float32))
                self.cache = self.batch

            # 少し前のデータベースをしばらく使う
            square_distances, indices = self.index.search(
                X_query.astype(np.float32), self.k
            )
            self.cache -= 1
            distances = np.sqrt(square_distances[0])
            indices = indices[0]

        # print(X_database.shape[0], nlist, t1 - t0, t2 - t1)

        return distances, indices

    def _sort_results(self, distances, indices):
        # 順番がランダムなのでソート
        arg_ind = np.argsort(distances)
        return distances[arg_ind], indices[arg_ind]

ではモジュールの使い方を確認してみましょう

?NeighborSearch

Init signature:
NeighborSearch(
    k: int,
    epsilon: float = None,
    metric: str = 'Euqlid',
    method: str = 'KNN',
    delta: float = 0.1,
    search_exculusion: int = 0,
    batch=5000,
    switch=0,
    reduction_dim=10,
)
Docstring:     
JIT用の近傍探索部分モジュール。各時刻について、それより前の時刻の観測から近傍を選ぶ。

    Attributes
    ----------
    distance_records : np.ndaraay
        近傍探索結果。時間数 x 近傍数(k) の二次元配列。各近傍サンプルの距離が入っている。

    indices_records : np.ndarray
        近傍探索結果。時間数 x 近傍数(k) の二次元配列。各近傍サンプルのindexが入っている。

    Methods
    -------
    run(data)
        全時間に対して近傍探索を実行。

    Examples
    --------
    >>> data = np.array(
    ...     [
    ...         [0, 0, 1],
    ...         [0, 0, 2],
    ...         [0, 0, 3],
    ...         [0, 0, 4],
    ...         [0, 0, 5],
    ...         [1, 0, 6],
    ...         [1, 0, 7],
    ...         [1, 0, 8],
    ...         [1, 0, 9],
    ...     ]
)
    >>> ns = NeighborSearch(k=3)
    >>> ns.run(data)
    ... (array([[-1.        , -1.        , -1.        ],
    ...         [-1.        , -1.        , -1.        ],
    ...         [-1.        , -1.        , -1.        ],
    ...         [ 1.        ,  2.        ,  3.        ],
    ...         [ 1.        ,  2.        ,  3.        ],
    ...         [ 1.41421356,  2.23606798,  3.16227766],
    ...         [ 1.        ,  2.23606798,  3.16227766],
    ...         [ 1.        ,  2.        ,  3.16227766],
    ...         [ 1.        ,  2.        ,  3.        ]]),
    ...  array([[-1, -1, -1],
    ...         [-1, -1, -1],
    ...         [-1, -1, -1],
    ...         [ 2,  1,  0],
    ...         [ 3,  2,  1],
    ...         [ 4,  3,  2],
    ...         [ 5,  4,  3],
    ...         [ 6,  5,  4],
    ...         [ 7,  6,  5]]))
Init docstring:
探索用パラメータ設定を行う。
KNNは近い順位にK個、ERNは距離epsion以内の近傍からランダムにK個。

Parameters
----------
k : int
    探索する近傍の数。KNNでもERNでも必須
epsilon : float, optional
    探索近傍の半径。ERNで必須, by default None
metric : str, optional
    距離指標。"Euqlid"、"Mahalanobis"、"PCA_Reduction" など , by default "Euqlid"
method : str, optional
    近傍選択法。"KNN"、"ERN"、"faiss_KNN"、"faiss_approximate_KNN"が選択可, by default "KNN"
delta : float, optional
    ERN時にサンプルがK個以下なら、K以上になるまでdeltaずつ半径を拡大する。, by default 0.1
search_exculusion : int, optional
    検索除外期間。近傍探索から直近のsearch_exculusion個のサンプルは除外, by default 0
batch : int, optional
    method="faiss_approximate_KNN" 選択時にバッチ処理を行う。batch個のサンプルが貯まるまで検索対象となるデータベースは更新されない, by default 5000
switch : int, optional
    method="faiss_approximate_KNN" 選択時に、非近似版と近似版の探索アルゴリズムをスイッチするタイミング。少数データ時(10000オーダー以下)は非近似版が早い, by default 0
reduction_dim : int, optional
    method="PCA_Reduction" 選択時に次元削減後の次元数, by default 10
Type:           type
Subclasses:     

ベースとなるモデルの用意

次に、JITにより繰り返し学習される軽量なモデルとして、Ridge回帰のモデルを用意しておきます。

後述の学習モジュールでは、適用対象の軽量モデルはscikit-learn likeな実装方式を持ったモデル(fit()などのメソッドを持つ)であれば利用可能です。

後述の学習モジュールのrun()関数では、各時刻における学習用のfit()関数の返り値が結果（メンバ）変数resultsに格納される仕組みになっています。 ここでは、後述するようなモデルの解釈を便利に行うため、sklearnのfit()関数の返り値のメンバ変数intercept_とcoef_に格納されている切片と重回帰係数を抽出して、それらの値からなる配列を返すようなラッパーを作成することとします。 また、scikit-learnのRidgeは正則化係alphaのスケールが学習データのサンプル数に依存してしまうため、ついでにそこも修正しておきます。

他にも、いくつかJITでよく使われるモデルのラッパーを以下に準備しておきます。(今回は採用しない手法も載せています)

# よく使われる便利なモデルのラッパー群例

from sklearn.linear_model import Ridge, Lasso
import numpy as np
from sklearn.decomposition import PCA
from sklearn.cross_decomposition import PLSRegression


class RidgeModel(Ridge):
    def __init__(self, alpha):
        """Loss上で学習データ数に結果が依存しないようスケーリングするRidge

        Parameters
        ----------
        alpha : float
            正則化係数
        """
        super().__init__(alpha=alpha, fit_intercept=True)

    def fit(self, X, y, **kwargs):
        res = super().fit(X, y, sample_weight=1 / y.shape[0])

        # 返り値は回帰係数と切片にしておく
        return np.array([*res.intercept_.flatten(), *res.coef_.flatten()])


class LassoModel(Lasso):
    def __init__(self, alpha):
        super().__init__(alpha=alpha, fit_intercept=True)

    def fit(self, X, y, **kwargs):
        res = super().fit(X, y)

        # 返り値は回帰係数と切片にしておく
        return np.array([*res.intercept_.flatten(), *res.coef_.flatten()])


class PLS_Model(PLSRegression):
    def fit(self, X, y, distances, **kwargs):
        res = super().fit(X, y)

        # 返り値は回帰係数と切片にしておく
        return np.array([*res.intercept_.flatten(), *res.coef_.flatten()])

学習モジュール

最後に、上記の近傍探索の結果によって出力された近傍データを使って、学習を行うプロセス全体を管理するモジュールを書きます。

run()メソッドではデータと近傍探索結果を読み込み、各時刻におけるモデルを学習してなんらかの学習結果を保存します。 今回は、後述の係数の解析のため、重回帰モデルの回帰係数と切片を学習結果として保存し、推論値の作成は別途保存された回帰係数と切片より再計算する方法をとります。

こちらも長いので折りたたんでおきます。

Show code cell content Hide code cell content

# JIT.py
# 出力された近傍データを使った学習を行う

import numpy as np
import copy
import warnings


class JIT:
    """JIT用の学習部分モジュール。近傍探索結果、データ、モデルを引数に、各時刻についてJIT学習を行う。

    Attributes
    ----------
    model : sklearn like object
        学習に使うモデルのインスタンス。model.fit()などが実行可能。`results[i]=model.fit()`と処理される。
    results : list[object]
        なんらかの学習結果を格納するリスト。run()時に初期化して渡せば np.ndarray などにしてメモリ効率良く保存することも可能。

    Methods
    -------
    run(data)
        全時間に対して学習を実行。

    Examples
    --------
    >>> # 適当なデータX,Yを生成======================================================
    >>> import numpy as np
    >>> np.random.seed(123)
    >>> # 適当なマルチモーダルデータX
    >>> d = 3
    >>> X1 = np.random.random(size=[1000, d])  # 範囲[0,1]
    >>> X2 = np.random.random(size=[1000, d]) - 1  # 範囲[-1,0]
    >>> X = np.concatenate([X1, X2], axis=0, dtype=float)
    >>> # 適当な重みwを使って一次元に
    >>> w = np.ones(shape=[d])
    >>> theta = np.pi / d * X @ w  # 範囲[-pi,pi]
    >>> # 適当な非線形関数
    >>> Y = np.cos(theta)

    >>> # 近傍探索================================================================
    >>> k = 20
    >>> search_exculusion = 10
    >>> ns = NeighborSearch(
    ...     k=k,
    ...     metric="Euqlid",
    ...     method="faiss_KNN",
    ...     search_exculusion=search_exculusion,
    ... )
    >>> distances_records, indices_records = ns.run(data=X)

    >>> # coef+interceptの結果が入る二次元配列の用意=================================
    >>> results = np.full(shape=[X.shape[0], X.shape[1] + 1], fill_value=np.nan)

    >>> # JIT予測================================================================
    >>> jit = JIT(model=RidgeModel(alpha=1.0))
    >>> results = jit.run(
    ...     data=X,
    ...     indices_recordes=indices_records,
    ...     results=results,
    ...     target_data=Y,
    ... )
    >>> intercepts = results[:, 0]
    >>> coefs = results[:, 1:]
    >>> Y_pred = np.sum(X * coefs, axis=1) + intercepts
    >>> value_exist = ~np.isnan(Y_pred)
    >>> R2 = 1 - np.mean((Y[value_exist] - Y_pred[value_exist]) ** 2) / np.var(
    ...     Y[value_exist]
    ... )
    >>> message = f"R^2:{R2}"
    >>> print(message)
    R^2:0.9110827833120044

    """

    def __init__(self, model):
        """JITで近傍データに対して学習を実行するモデルの設定を行う。sklearn-likeなインスタンスを設定。

        Parameters
        ----------
        model : sklearn like object
            JITで近傍データに対して学習を実行するモデルのインスタンス。model.fit()とmodel.predict()を使えるもの。

            # model 実装例は`/JIT/_util_models.py`を参照。`results[i]=model.fit()`と処理される。
        """
        self.model = model

    def run(
        self,
        data: np.ndarray,
        indices_recordes: np.ndarray,
        results: list = None,
        distances_records: np.ndarray = None,
        target_data: np.ndarray = None,
    ):
        """データ、近傍探索結果などを引数にJITの学習を実行。

        Parameters
        ----------
        data : np.ndarray
            時間数 x 特徴量数 の二次元配列。教師あり学習の時は説明変数。
        indices_recordes : np.ndarray[int]
            近傍探索結果。時間数 x 近傍数(k) の二次元配列。各時刻の近傍サンプルのindexが入っている。
        results : list, optional
            `results[i]=model.fit()`と処理される。np.ndarrayなどにして初期化して渡せばメモリ効率良く保存することも可能, by default [None]*time
        distances_records : np.ndaraay
            近傍探索結果。時間数 x 近傍数(k) の二次元配列。各近傍サンプルの距離が入っている, by default 2d np.ndarray of np.nan
        target_data : np.ndarray, optional
            教師あり学習の場合教師データが入る, by default None

        Returns
        -------
        list[object]
            self.resultsを返す。学習結果のリスト。`results[i]=model.fit()`と処理される。時間数の配列サイズはキープして、値がない部分は初期値で埋めている。
        """
        # データの型チェックなど
        self.data = data  # DataFrameにする？
        self.T, self.D = self.data.shape
        if results is None:
            self.results = [None] * self.T
        else:
            self.results = results  # 最初に初期化して渡す

        self.indeices_records = indices_recordes
        assert self.T == self.indeices_records.shape[0]

        self.distances_records = distances_records
        if self.distances_records is None:
            self.distances_records = np.full(
                shape=self.indeices_records.shape, fill_value=np.nan
            )
        else:
            assert self.T == self.distances_records.shape[0]

        self.target_data = target_data
        if self.target_data is None:
            self.concat_data = self.data
        else:
            assert self.T == self.target_data.shape[0]
            self.concat_data = np.concatenate(
                [self.data, self.target_data.reshape(self.T, -1)], axis=1
            )

        # JIT本体
        for i in range(self.T):
            neighbor_data = self._extract_neighbor_data(self.indeices_records[i])

            if neighbor_data is None:
                pass
            else:
                neighbor_X = neighbor_data[:, : self.D]
                neighbor_Y = neighbor_data[:, self.D :]
                # 教師あり & 教師なしもkwargs利用で全部これでいく
                result = copy.deepcopy(
                    self.model.fit(
                        X=neighbor_X,
                        y=neighbor_Y,
                        distances=self.distances_records[i][
                            ~(self.distances_records[i] < 0)
                        ],
                    )
                )

                self.results[i] = result

        return self.results

    def _extract_neighbor_data(self, indices) -> np.ndarray:
        # 初期値-1の処理とかNoneの処理考える
        if np.all(indices == -1):
            # 近傍数が足りない期間
            neighbor_data = None
        elif np.any(indices == -1):
            # データがボロノイ領域に十分になかったとき
            indices = indices[~(indices == -1)]
            message = f"Caution!: Neighbor Data is Smaller Than K, The Size is {indices.shape[0]}"
            warnings.warn(message)
            neighbor_data = self.concat_data[indices]
        elif indices.shape[0] < self.D:
            message = f"Caution!: Neighbor Data is Smaller Than D, The Size is {indices.shape[0]}"
            warnings.warn(message)
            neighbor_data = self.concat_data[indices]
        else:
            neighbor_data = self.concat_data[indices]

        return neighbor_data

ではモジュールの使い方を確認してみましょう。

?JIT

Init signature: JIT(model)
Docstring:     
JIT用の学習部分モジュール。近傍探索結果、データ、モデルを引数に、各時刻についてJIT学習を行う。

Attributes
----------
model : sklearn like object
    学習に使うモデルのインスタンス。model.fit()などが実行可能。`results[i]=model.fit()`と処理される。
results : list[object]
    なんらかの学習結果を格納するリスト。run()時に初期化して渡せば np.ndarray などにしてメモリ効率良く保存することも可能。

Methods
-------
run(data)
    全時間に対して学習を実行。

Examples
--------
>>> # 適当なデータX,Yを生成======================================================
>>> import numpy as np
>>> np.random.seed(123)
>>> # 適当なマルチモーダルデータX
>>> d = 3
>>> X1 = np.random.random(size=[1000, d])  # 範囲[0,1]
>>> X2 = np.random.random(size=[1000, d]) - 1  # 範囲[-1,0]
>>> X = np.concatenate([X1, X2], axis=0, dtype=float)
>>> # 適当な重みwを使って一次元に
>>> w = np.ones(shape=[d])
>>> theta = np.pi / d * X @ w  # 範囲[-pi,pi]
>>> # 適当な非線形関数
>>> Y = np.cos(theta)

>>> # 近傍探索================================================================
>>> k = 20
>>> search_exculusion = 10
>>> ns = NeighborSearch(
...     k=k,
...     metric="Euqlid",
...     method="faiss_KNN",
...     search_exculusion=search_exculusion,
... )
>>> distances_records, indices_records = ns.run(data=X)

>>> # coef+interceptの結果が入る二次元配列の用意=================================
>>> results = np.full(shape=[X.shape[0], X.shape[1] + 1], fill_value=np.nan)

>>> # JIT予測================================================================
>>> jit = JIT(model=RidgeModel(alpha=1.0))
>>> results = jit.run(
...     data=X,
...     indices_recordes=indices_records,
...     results=results,
...     target_data=Y,
... )
>>> intercepts = results[:, 0]
>>> coefs = results[:, 1:]
>>> Y_pred = np.sum(X * coefs, axis=1) + intercepts
>>> value_exist = ~np.isnan(Y_pred)
>>> R2 = 1 - np.mean((Y[value_exist] - Y_pred[value_exist]) ** 2) / np.var(
...     Y[value_exist]
... )
>>> message = f"R^2:{R2}"
>>> print(message)
R^2:0.9110827833120044
Init docstring:
JITで近傍データに対して学習を実行するモデルの設定を行う。sklearn-likeなインスタンスを設定。

Parameters
----------
model : sklearn like object
    JITで近傍データに対して学習を実行するモデルのインスタンス。model.fit()とmodel.predict()を使えるもの。

    # model 実装例は`/JIT/_util_models.py`を参照。`results[i]=model.fit()`と処理される。
Type:           type
Subclasses:     

トイデータに対する実験

ここでは実際に非線形、非定常なデータを人工的に生成してJITの性質を確認します。

データ生成

多変量の説明変数\(\boldsymbol{x}_t\)の分布として、以下の分布を用意します。時間インデックス\(t\)の経過によるこの二つの分布の遷移は、非定常なクラスタの変化(共変量シフト)を意識しています。

\[\begin{align*} \begin{cases} \boldsymbol{x_t}(\in \mathbb{R}^3)\sim \text{Uniform}([0,1]\times[0,1]\times[0,1]) & \text{for} \; 0\leq t<1000\\ \boldsymbol{x_t}(\in \mathbb{R}^3)\sim \text{Uniform}([-1,0]\times[-1,0]\times[-1,0]) & \text{for} \; 1000\leq t<2000 \end{cases} \end{align*}\]

目的変数を生成する非線形関数 \(f(\cdot)\) は解析的に微分を計算できるように、以下のものを用意します。

\[\begin{align*} f(\boldsymbol{x})=\cos(2\theta (\boldsymbol{x})) \end{align*}\]

\[\begin{align*} \theta (\boldsymbol{x})=\pi\cdot\frac{\boldsymbol{1}^\text{T} \boldsymbol{x}}{3} \quad (\in[-\pi,\pi]) \end{align*}\]

\[\begin{align*} y_t=f(\boldsymbol{x}_t)+\epsilon,\quad \epsilon \sim \mathcal{N}(0,0.1) \end{align*}\]

ただし\(\boldsymbol{1}\)は要素が全て1の3次元ベクトルです。

では実際にコードでデータを生成してみましょう。

import numpy as np

np.random.seed(123)

# 非定常な説明変数X
d = 3
N_data = 2000
X1 = np.random.random(size=[N_data // 2, d])  # 範囲[0,1]
X2 = np.random.random(size=[N_data // 2, d]) - 1  # 範囲[-1,0]

X = np.concatenate([X1, X2], axis=0, dtype=float)

# 重み1を使って一次元に
ones = np.ones(shape=[d])
theta = np.pi / d * X @ ones  # 範囲[-pi,pi]

# 非線形関数により目的変数を生成
epsilon = np.random.normal(loc=0, scale=0.1, size=theta.shape[0])

Y = np.cos(2 * theta) + epsilon

本来4次元となる\((\boldsymbol{x}_t,y_t)\)の関係を二次元に可視化するために、\(\theta (\boldsymbol{x}_t)\)を用いてこれを横軸、\(y_t\)を縦軸に、データをプロットすると以下のようになります。

from matplotlib import pyplot as plt

t = np.arange(-np.pi, np.pi, 0.01)
plt.plot(t, np.cos(2 * t), "-", label=r"$y=\cos(2\theta)$")

Q = Y.shape[0] // 2
for i in range(2):
    plt.plot(
        theta[Q * i : Q * (i + 1)],
        Y[Q * i : Q * (i + 1)],
        "o",
        alpha=0.1,
        label=f"observed data ${Q*i}\leq t<{Q*(i+1)}$",
    )


plt.xlabel(r"$\theta(x_t)$")
plt.ylabel(r"$y_t$")
plt.legend(loc="upper left", bbox_to_anchor=(1, 1))
plt.show()

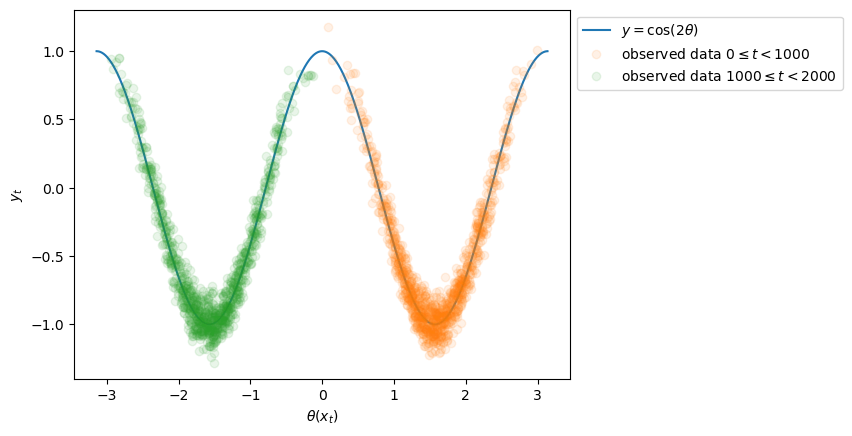
通常の線形モデルではモデリング困難な非線形なデータが得られていることがわかります。

また、例えばNNやガウス過程などの非線形モデルで前半のみのデータ(オレンジ)で学習した場合、学習データの範囲外(≒外挿範囲)に存在する後半のデータ(緑)への汎化性能は保証できません。周期性などの事前知識を導入しない限りは、おそらくオレンジの谷型が続くかなだらかになっていく二次関数的な形が学習される場合が多いと考えられます。JITでは繰り返し学習を行うことで後半のデータに対しても高い精度で予測を返すことができます。

近傍探索

近傍探索モジュールを使って全時刻データに対して一括して近傍探索を実施します。

時刻\(T\)の時、入力\(\boldsymbol{x}_T\)に対して現時点までの観測データ\(D=\{(\boldsymbol{x}_t,y_t)|\, t\in [0,T-1]\}\)の中から入力のK近傍、つまり距離が近い順に\(K\)個を抜き出します。 したがってこのモジュールの出力は「各時刻における選ばれたデータのindex群」になり、全ての時刻のものをまとめると全時刻数 × 近傍数Kの2次元配列になることに注意して下さい。

近傍のindex群と同時に、それぞれのindexと対応する入力点からの距離も出力されます。この距離は、例えば学習アルゴリズムによってはLossに対するサンプルごとの重みとして利用することができます(後述)。

# 近傍探索
k = 100
ns = NeighborSearch(k=k, metric="Euqlid", method="faiss_KNN")
distances_records, indices_records = ns.run(data=X)

distances_records.shape, indices_records.shape

((2000, 100), (2000, 100))

学習と推論

次に先ほどの近傍探索の結果を利用して学習と推論を行います。

※ ベースとなるモデルの用意発展編：Locally Weighted

ここで、JITでしばしば使われるベースモデルである、Locally Weighted (LW) という方法を紹介しておきます。 Locally Weighted では近傍探索時に求まった距離を利用して、データ1サンプルごとに重み\(w_i\)を作成し、回帰の精度向上に活かします。

\(d_i=d\left(\boldsymbol{x}_i, \boldsymbol{x}\right)\)が入力との距離、\(h\)がそのバンド幅(ハイパーパラメータ)として、重みの形としては以下のようなものなどがよく使われます。

• ガウス関数

\[\begin{align*} w_i=w_i(d_i,h)=-\frac{1}{\sqrt{2\pi h^2}}\exp(-\frac{{d_i}^2}{2h^2}) \end{align*}\]

• Epanechnikov関数

\[\begin{align*} w_i=w_i(d_i,h)=-\frac{3}{4h}\left(1-\left(\frac{d_i}{h}\right)^2\right) \end{align*}\]

これらの重み関数は距離\(d_i\)に対しての単調減少関数になっており、直感的には「入力に近い(=距離が小さい)サンプル\((\boldsymbol{x}_i,y_i)\)の方がモデリングにおける重要度が高いはず」という期待を盛り込むことができます。

有名なものでは以下が知られています。

Locally Weighted Average (LWA) :
単に近傍サンプルの目的変数を近さに応じて重み付き平均したものを出力とします。\(i\)は近傍データに対して振り直したindexです。

\[\begin{align*} \quad \hat{y}=\sum_{i=1}^k {\color{red} w_i} y_i \end{align*}\]

Locally Weighted Regression (LWR) :
通常、線形回帰モデルでは二乗誤差の合計を最小化するように学習を行います。しかし、LWRではそれぞれの二乗誤差に対して距離に応じた重みを掛け算することで、距離の近いサンプルを重要視したモデリングが可能です。\(i\)は近傍データに対して振り直したindexです。

\[\begin{align*} \hat{y}=\hat{\boldsymbol{\beta}}^T \tilde{\boldsymbol{x}},\quad \tilde{\boldsymbol{x}}:=\left[\begin{array}{l}1 \\ \boldsymbol{x}\end{array}\right] \end{align*}\]

\[\begin{align*} \hat{\boldsymbol{\beta}}:=\underset{\boldsymbol{\beta}}{\operatorname{argmin}} \left(\sum_{i=1}^k {\color{red} w_i} \left(y_i-\boldsymbol{\beta}^T \tilde{\boldsymbol{x}}_i\right)^2\right), \quad \tilde{\boldsymbol{x}}_i:=\left[\begin{array}{c} 1 \\ \boldsymbol{x}_i \end{array}\right] \end{align*}\]

それではLocally Weighted化したRidgeモデルを作成します。今回のトイデータ分析ではこちらを用いることにします。

class LW_RidgeModel(Ridge):
    def __init__(self, alpha, h=0.5):
        """Locally Weighted なRidge。Loss上で学習データ数に結果が依存しないようスケーリング

        Parameters
        ----------
        alpha_ : float
            Loss上で学習データ数に結果が依存しないようスケーリングが行われる正則化係数
        h : foat
            重みづけカーネルのバンド幅
        """
        self.h = h
        super().__init__(alpha=alpha, fit_intercept=True)

    def fit(self, X, y, distances, **kwargs):
        v = self.h**2
        # ガウスカーネル
        kernel = np.exp(-(distances**2) / (2 * v)) / np.sqrt(2 * np.pi * v)
        sample_weight = kernel / np.sum(kernel)

        res = super().fit(X, y, sample_weight=sample_weight)

        # 返り値は回帰係数と切片にしておく
        return np.array([*res.intercept_.flatten(), *res.coef_.flatten()])

# coef+interceptの結果が入る二次元配列
results = np.full(shape=[X.shape[0], X.shape[1] + 1], fill_value=np.nan)

jit = JIT(model=LW_RidgeModel(alpha=0.001, h=0.1))
results = jit.run(
    data=X,
    indices_recordes=indices_records,
    results=results,
    target_data=Y,
    distances_records=distances_records,
)

学習したパラメータに基づいて予測

JITモジュールのresultsメンバ変数から各時刻で学習された回帰係数と切片を取り出して、予測をやってみましょう。

intercepts = results[:, 0]
coefs = results[:, 1:]

Y_pred = np.sum(X * coefs, axis=1) + intercepts

t = np.arange(-np.pi, np.pi, 0.01)
plt.plot(t, np.cos(2 * t), "-", label=r"$y=\cos(2\theta)$")
plt.plot(theta, Y, "o", alpha=0.1, label="observed data")
plt.plot(theta, Y_pred, "o", alpha=0.1, label="predicted data")
plt.xlabel(r"$\theta(x_t)$")
plt.ylabel(r"$y_t$")
plt.legend(loc="upper left", bbox_to_anchor=(1, 1))
plt.show()

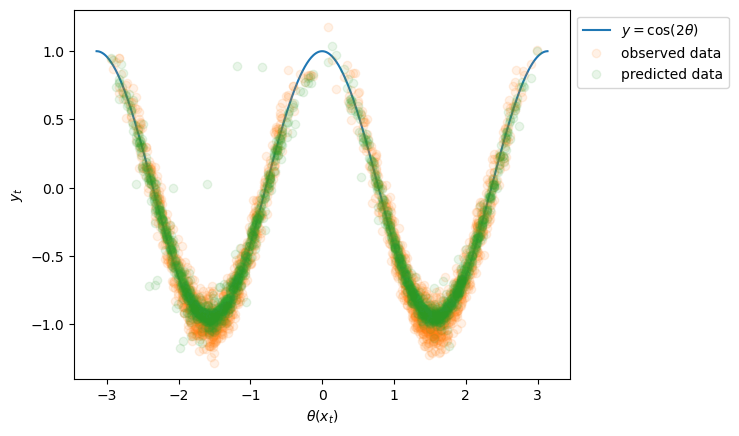
評価/考察

予測精度

精度の評価をしてみましょう、今回は\(R^2\)値とRMSEを確認します。

value_exist = ~np.isnan(Y_pred)

R2 = 1 - np.mean((Y[value_exist] - Y_pred[value_exist]) ** 2) / np.var(Y[value_exist])
RMSE = np.sqrt(np.mean((Y[value_exist] - Y_pred[value_exist]) ** 2))
message = f"R^2:{R2}, RMSE:{RMSE}"
print(message)

R^2:0.9268724226911659, RMSE:0.13202466839692711

両者から、おそらく非常に高い精度で予測できていることがわかります。

ノイズを除いた真の値(\(\cos(2\theta)\))との差は以下のようになります。

value_exist = ~np.isnan(Y_pred)

Y_true = np.cos(2 * theta)
R2 = 1 - np.mean((Y_true[value_exist] - Y_pred[value_exist]) ** 2) / np.var(
    Y[value_exist]
)
RMSE = np.sqrt(np.mean((Y_true[value_exist] - Y_pred[value_exist]) ** 2))
message = f"R^2:{R2}, RMSE:{RMSE}"

print(message)

R^2:0.9675561548902277, RMSE:0.08793882373448625

以上の結果より、複雑な非線形関数を線形モデルを元にJITで見事にモデリングすることができました。

回帰係数の確認

Just-In-Timeモデルの魅力の一つは高い解釈性です。通常非線形モデルは、線形モデルと違って回帰係数を確認することができず、偏微分値などを計算する必要があります。しかしモデルによってはそれが容易ではなかったり、その意味合いも判然としなかったりする場合があります。

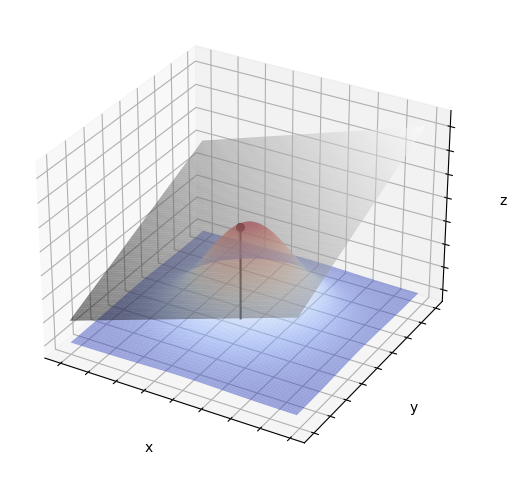
JITでは、図形的には「入力点近傍における非線形関数の接線(接平面)」として、学習されたベース線形モデルの回帰係数などを解釈できます。また、入力点近傍において線形回帰モデルの係数と同等の解釈が部分的に可能です。

※ 接平面のイメージ図と描画コード(例：\(z=f(x,y)\))

(描画用のコードは本編と外れるので折りたたんでおきます。)

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
from IPython.display import display, Math
from sympy import *
from sympy.plotting import plot3d

init_printing()

#
# 関数 f(x,y)=exp(-(x**2 + y**2))　と、 (x0, y0) における接平面をプロットする
#

x0, y0 = -0.1, -0.1

# sympy変数
x, y = symbols("x y")

# 関数の定義（お好きな関数をどうぞ）
f = exp(-(x**2 + y**2))
# f = 3*(x+1)**2 + 4*(y+1)**2 + 2
# print("回帰曲面")
# display(Math(rf"f(x, y) = {latex(f)}"))

# z0 = f(x0, y0)　の計算
z0 = f.subs([(x, x0), (y, y0)])

# sympy上でプロットしてみる
# plot3d(f, (x, -2, 2), (y, -2, 2))
# plt.show()

# 偏導関数関数の計算
dfdx = diff(f, x)
dfdy = diff(f, y)
# print("偏導関数")
# display(Math(rf"\frac{{\partial f}}{{\partial x}} = {latex(dfdx)}"))
# display(Math(rf"\frac{{\partial f}}{{\partial y}} = {latex(dfdy)}"))

# (x0, y0)における偏微分係数の計算
wx = dfdx.subs([(x, x0), (y, y0)])
wy = dfdy.subs([(x, x0), (y, y0)])

# 接平面の関数　z(x,y)
z = z0 + wx * (x - x0) + wy * (y - y0)

# sympy関数 f を　pythonの関数　func(), func_plane()　に移植
func = lambdify((x, y), f, "numpy")
func_plane = lambdify((x, y), z, "numpy")

# sympyは用済みなので、sympy変数 x, y　と関数　f, z を消す（プロットに同じ名前の変数を使いたいので）
del f, x, y, z

#
# matplotlibを使ってプロット
#

# プロット領域の作成
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection="3d")

# x, y の範囲を設定
x = np.arange(-2, 2, 0.05)
y = np.arange(-2, 2, 0.05)
x, y = np.meshgrid(x, y)  # x, y　に上書き

# グリッド上での曲面func()と・接平面func_plane()の値の計算
z = func(x, y)
z_plane = func_plane(x, y)

# プロット
ax.plot_surface(
    x, y, z, rstride=1, cstride=1, cmap="coolwarm", linewidth=0.3, alpha=0.5
)
ax.plot_surface(
    x, y, z_plane, rstride=1, cstride=1, cmap="gray", linewidth=0.3, alpha=0.5
)
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("z")
ax.set_xticklabels([])
ax.set_yticklabels([])
ax.set_zticklabels([])
ax.scatter(x0, y0, func(x0, y0), marker="o", s=30, c="black")
ax.plot([x0, x0], [y0, y0], [0, func(x0, y0)], c="black")
plt.show()

解析的な傾きの計算

非線形関数\(f(\boldsymbol{x})\)を線形で近似したとき、入力点\(\boldsymbol{x}_\text{q}\)の周りでテイラー近似を計算すると、以下のようになります。

\[\begin{align*} f(\boldsymbol{x})=f(\boldsymbol{x}_\text{q})+\boldsymbol{\nabla}f(\boldsymbol{x}_\text{q})^\text{T}(\boldsymbol{x}-\boldsymbol{x}_\text{q})+o({|\boldsymbol{x}-\boldsymbol{x}_\text{q}|}) \end{align*}\]

よって、線形回帰モデルをベースとしたJITは、非線形関数の2次以降の部分を線形回帰の誤差として処理し、傾き\(\boldsymbol{\nabla}f(\boldsymbol{x}_\text{q})\)と切片\(f(\boldsymbol{x}_\text{q})\)を求めるように動作すると期待できます。

したがって求まっていて欲しい局所的な傾き\(\boldsymbol{\nabla}f(\boldsymbol{x}_\text{q})\)はチェインルールより、以下のように計算できます。

\[\begin{align*} \boldsymbol{\nabla}f(\boldsymbol{x}_\text{q})&=-2\sin(2\theta (\boldsymbol{x}))\frac{\text{d}\theta (\boldsymbol{x})}{\text{d}\boldsymbol{x}}\\ &=-2\sin(2\theta (\boldsymbol{x}))\frac{\pi}{3}\cdot\boldsymbol{1}\quad \cdots (\star) \end{align*}\]

解析的な傾きと回帰係数との比較

では、解析的な値とJITの過程で学習された値を比較してみましょう。

傾きは実際には3次元ベクトルですが、代表として1次元目を比較します。後ろから50サンプルの傾きを比較してみましょう。

nabla = -np.sin(2 * theta) * 2 * np.pi / 3

M = 50
i = 0
plt.plot(np.arange(N_data - M, N_data), coefs[-M:, i], label="learned coefficient")
plt.plot(np.arange(N_data - M, N_data), nabla[-M:], label="analytical coefficient")
plt.xlabel(r"$t$")
plt.ylabel(r"$\nabla f(x_q)$")
plt.legend(loc="upper left", bbox_to_anchor=(1, 1))
plt.show()

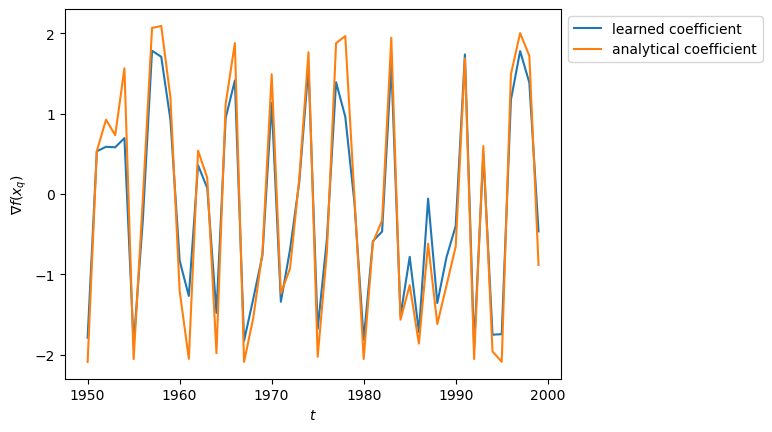
非常に高い相関を持っているため、うまく係数推定ができていそうです。

では別の形での可視化を試みてみましょう。 先ほどの\((\theta(\boldsymbol{x}_t),y_t)\)の二次元グラフに換算した傾きを表示してみます。

• 解析的な傾き：

  • \(\frac{\text{d}f}{\text{d}\theta}=-2\sin(2\theta)\)

• 学習された傾き：

  • 上述の\((\star)\)式より、\(-2\sin(2\theta)\frac{\pi}{3}\cdot\boldsymbol{1}=\boldsymbol{\nabla}f(\boldsymbol{x_\text{q}})\)なので、左から\(\boldsymbol{1}^\text{T}\)をかけて整理すると、

  \[\begin{align*} \frac{\text{d}f}{\text{d}\theta}=-2\sin(2\theta)=\frac{\boldsymbol{1}^\text{T}\boldsymbol{\nabla}f(\boldsymbol{x_\text{q}})}{\pi} \end{align*}\]

ここから換算します。3つの回帰係数の合計を\(\boldsymbol{1}^\text{T}\boldsymbol{\nabla}f(\boldsymbol{x_\text{q}})\)の推定値として、計算することにします。

各予測点ごとに傾きを\((\theta(\boldsymbol{x}_t),y_t)\)平面に換算し、対応する直線をプロットします。予測点は50ステップごとにサンプリングします。予測点の色とその予測点に対応する直線の色は同じにします。

grad = np.sum(coefs, axis=1) / np.pi

intercepts = results[:, 0]
coefs = results[:, 1:]

Y_pred = np.sum(X * coefs, axis=1) + intercepts

t = np.arange(-np.pi, np.pi, 0.01)
plt.plot(t, np.cos(2 * t), "-", label=r"$y=\cos(2\theta)$")

cmap = plt.get_cmap("tab10")
freq = 50
for i in range(N_data):
    if i % freq == 0:
        if i == 1000:
            plt.plot(
                t,
                grad[i] * (t - theta[i]) + Y_pred[i],
                alpha=0.3,
                color=cmap(i // freq % 10),
                label="predicted gradients",
            )
            plt.plot(
                theta[i],
                Y_pred[i],
                "o",
                color=cmap(i // freq % 10),
                label="predicted data",
            )
            plt.text(theta[i], Y_pred[i], " ←t=1000")
        else:
            plt.plot(
                t,
                grad[i] * (t - theta[i]) + Y_pred[i],
                alpha=0.3,
                color=cmap(i // freq % 10),
            )
            plt.plot(theta[i], Y_pred[i], "o", color=cmap(i // freq % 10))


plt.ylim(-1.45, 1.45)

plt.xlabel(r"$\theta(x_t)$")
plt.ylabel(r"$y_t$")
plt.legend(loc="upper left", bbox_to_anchor=(1, 1))
plt.show()

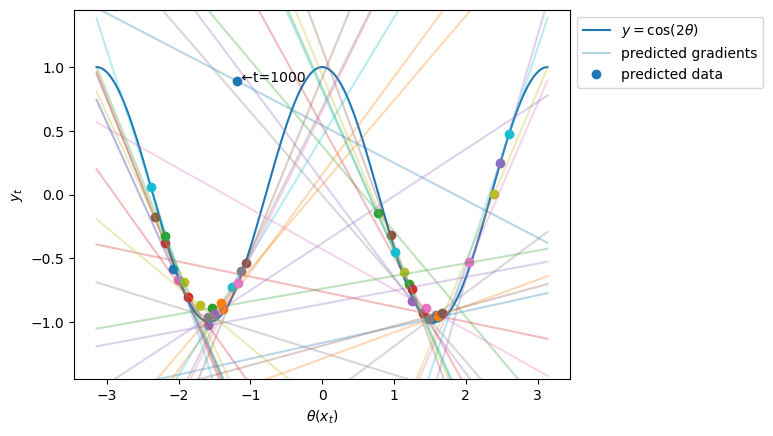
概ね包絡線のような図が描けており、各予測点における接線(接平面)の傾きがJITにより求まっていることが確認できます。

また、傾きと予測値を多く外している点は、\(t=1000\)、つまり新しい分布への切り替わり点であり、分布シフト先のデータがまだ十分に集まっていないので動作していない様子がよくわかります。

近傍として選ばれたサンプルの可視化

PCA上での動き

近傍として選ばれたサンプルの動きをPCA平面上でアニメーション表示します。これは実際のデータ分析においてはJITがうまく動いているかなどの解釈に非常に役に立ちます。

from sklearn.decomposition import PCA
from matplotlib.animation import ArtistAnimation
from IPython.display import HTML

# fpsを決定。step回に1回frameを作成して動画にする。
step = 100
# アニメーション表示の際のフレーム間隔(milliseconds)。
interval = 300

xlim = None
ylim = None


pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)

fig = plt.figure()
# グラフの設定
# plt.axes().set_aspect("equal")

frames = []
step_count = 0
first = True
for i in np.arange(0, N_data):

    if np.all(indices_records[i] == -1):
        pass
    else:
        if step_count % step == 0:
            # plt.xlim(xlim[0], xlim[1])
            # plt.ylim(ylim[0], ylim[1])

            X_then_pca = X_pca[:i]
            X_query_pca = X_pca[i]
            X_neighbors_pca = X_pca[indices_records[i]]

            ## 全観測(未来含め)をプロット
            im0 = plt.scatter(
                X_pca[:, 0], X_pca[:, 1], c="grey", label="all data (including future)"
            )
            ## 現時点までの観測をプロット
            im1 = plt.scatter(
                X_then_pca[:, 0],
                X_then_pca[:, 1],
                c="blue",
                alpha=0.3,
                label="observed data",
            )
            ## 選ばれた近傍をプロット
            im2 = plt.scatter(
                X_neighbors_pca[:, 0],
                X_neighbors_pca[:, 1],
                c="yellow",
                alpha=0.3,
                label="neighbor data",
            )
            ## クエリをプロット
            im3 = plt.scatter(
                X_query_pca[0], X_query_pca[1], c="red", label="query input"
            )

            if first:
                plt.xlabel("Pricipal Componet 1")
                plt.ylabel("Pricipal Componet 2")
                plt.legend(loc="upper left", bbox_to_anchor=(0, 1))
                first = False

            frame = [im0, im1, im2, im3]
            frames.append(frame)
        step_count += 1

# 描画
ani = ArtistAnimation(fig, frames, interval=interval)
html = HTML(ani.to_jshtml())
display(html)
# ani.save(name)

plt.close()

Once Loop Reflect

クラスターを跨がずに近傍を選択できている様子や、クラスターが切り替わった直後は上手く近傍を選べていない様子が見られます

時間軸上での動き

時間軸で見た時にどのサンプルが選ばれているのか確認します。

from matplotlib.animation import ArtistAnimation
from IPython.display import HTML

# fpsを決定。step回に1回frameを作成して動画にする。
step = 100
# アニメーション表示の際のフレーム間隔(milliseconds)。
interval = 300

# pandas.SeriesのTimeIndexなど。時間軸に表示するラベル
time_index = np.arange(0, N_data)


xlim = None
ylim = None


fig = plt.figure()
# グラフの設定
# plt.axes().set_aspect("equal")

frames = []
step_count = 0
first = True
for i in np.arange(0, N_data):

    if np.all(indices_records[i] == -1):
        pass
    else:
        if step_count % step == 0:

            selected_indices = indices_records[i]
            im0 = plt.vlines(
                time_index[selected_indices],
                0,
                1,
                colors="blue",
                alpha=0.3,
                label="neighbor data",
            )
            im1 = plt.vlines(
                time_index[i], 0, 1, colors="red", label="query input (current time)"
            )

            if first:
                plt.xlabel("Time Index")
                plt.legend(loc="upper right", bbox_to_anchor=(1, 1))
                first = False

            frame = [im0, im1]
            frames.append(frame)
        step_count += 1

# 描画
ani = ArtistAnimation(fig, frames, interval=interval)
html = HTML(ani.to_jshtml())
display(html)
# ani.save(name)

plt.close()

Once Loop Reflect

クラスターが切り替わった後は時間的に直近のデータ(クラスターが同じデータ)が選ばれていることが時間軸の面からも確認できます。

最後に：補足

今回は、Just-In-Timeモデルという非線形、非定常対応のフレームワークを紹介しました。

JITはそのシンプルな構成から、様々な手法に適用した応用例なども考えられます。手前味噌ですが、ごちきかの中の人達の論文「Causal Discovery for Non-stationary Non-linear Time Series Data Using Just-In-Time Modeling」では、因果探索というデータから変数間の因果関係を推定する分野において、JITを適用し線形手法LiNGAMを非線形/非定常に拡張した手法を提案しています。

JITの主な課題点はメモリと計算量におけるスケーラビリティです。現実的には過去のデータを全て保存して毎回検索すると、ストレージやメモリの限界を超えたり、近傍探索(つまりは推論)にかなりの時間がかかってしまうなど、いずれ莫大なコストがかかるようになってしまうので、例えば直近1年分のデータを保持しそのデータベース内でJITを動かすといった対処法が一般的です。近傍探索を行わず、単に直近のデータのみで学習して、改めて学習したモデルに入力を行い出力を作成する方式をMoving Window (MW) と呼びますが、部分的に類似点があります。他にも、計算量やメモリ使用を抑える方法はいくつか工夫の余地があるので、研究してみて下さい。

参考文献

• 山本茂, Just-In-Time 予測制御: 蓄積データに基づく予測制御, 計測と制御, Vol. 52, No. 10, pp. 878–884, 2013

• Anders Stenman, Fredrik Gustafsson, and Lennart Ljung, Just in time models for dynamical systems, In Proceedings of 35th IEEE Conference on Decision and Control, volume 1, pages 1115–1120. IEEE, 1996

• Daigo Fujiwara, Kazuki Koyama, Keisuke Kiritoshi, Tomomi Okawachi, Tomonori Izumitani, and Shohei Shimizu. Causal discovery for non-stationary non-linear time series data using just-in-time modeling. In 2nd Conference on Causal Learning and Reasoning, 2023.