VAR-LiNGAMによる時系列データの因果探索#

LiNGAMによる因果探索（応用編）では因果探索のモデルの一つであるLiNGAMおよびそのパラメータ推定について、前処理や推定結果の解釈、信頼度評価の方法についても併せて解説しました。

本稿ではLiNGAMを時系列データに対して拡張したVAR-LiNGAM[3]の解説、およびPythonとlingamライブラリ用いたVAR-LiNGAMによる分析の方法について説明します。

VAR-LiNGAMの定義#

VAR-LiNGAMとは、[3]にて提案された、時系列データ\(\mathbf{x}(0), \mathbf{x}(1), \dots , \mathbf{x}(T-1) \in \mathbb{R}^d\)における変数間の因果関係を表すモデル、およびそのパラメータ推定方法のことです。

VAR-LiNGAMは以下の数式を満たすモデルとして定義されます：

\[ \mathbf{x}(t) = \sum_{\tau=1}^p \mathbf{B}_\tau \mathbf{x}(t-\tau) + \mathbf{B}_0 \mathbf{x}(t) + \mathbf{e}(t) \]

ただし、

ノイズ\(\mathbf{e}(t) \in \mathbb{R}^d\)は独立同分布に従い、かつ各成分は独立である
ノイズ\(\mathbf{e}(t) \in \mathbb{R}^d\)の各成分の従う分布は正規分布ではない
\(\mathbf{B}_\tau \in \mathbb{R}^{d \times d}\)であり、\(\mathbf{B}_0\)はDAG（有向非巡回グラフ）の隣接行列に対応する

とします。ここから、VAR-LiNGAMはLiNGAMに過去からの影響の項\(\sum_{\tau=1}^p \mathbf{B}_\tau \mathbf{x}(t-\tau)\)を追加したものととらえることができます。LiNGAMについてはLiNGAMによる因果探索（基本編）もご参照ください。

そして時系列データ\(\mathbf{x}(0), \mathbf{x}(1), \dots , \mathbf{x}(T-1) \in \mathbb{R}^d\)が与えられたとき、データの生成過程がVAR-LiNGAMの仮定を満たしていれば変数間の因果関係、すなわち上記の式における\(\mathbf{B}_\tau\)を推定することができます。

本稿ではPythonとlingamライブラリを用いた、時系列データにおける変数間の因果関係の推定およびその結果の評価の実行例を紹介します。

VAR-LiNGAMのパラメータ推定#

VAR-LiNGAMのパラメータ推定方法は[3]で述べられているようにいくつかありますが、ここではlingamライブラリで実装されているTwo-Stage Methodについて解説します。

まず、下にVAR-LiNGAMの定義式を再掲します：

\[ \mathbf{x}(t) = \sum_{\tau=1}^p \mathbf{B}_\tau \mathbf{x}(t-\tau) + \mathbf{B}_0 \mathbf{x}(t) + \mathbf{e}(t) \]

この式から\(\mathbf{B}_0 \mathbf{x}(t)\)を左辺に移項したのち、両辺に左から\(\left(\mathbf{I}-\mathbf{B}_0 \right)^{-1}\)を掛けると

\[ \mathbf{x}(t) = \sum_{\tau=1}^p \underbrace{\left(\mathbf{I}-\mathbf{B}_0 \right)^{-1}\mathbf{B}_\tau}_{= \mathbf{A}_\tau} \mathbf{x}(t-\tau) + \underbrace{\left(\mathbf{I}-\mathbf{B}_0 \right)^{-1}\mathbf{e}(t)}_{= \mathbf{r}(t)} \]

となり、右辺から同時刻の値\(\mathbf{x}(t)\)の影響が消えたVARモデルとなります。したがってVARモデルの推定と同様にしてモデル

\[ \mathbf{x}(t) = \sum_{\tau=1}^p \mathbf{A}_\tau \mathbf{x}(t-\tau) + \mathbf{r}(t) \]

の係数\(\mathbf{A}_\tau\)を推定できます。すると残差\(\mathbf{r}(t)=\left(\mathbf{I}-\mathbf{B}_0 \right)^{-1}\mathbf{e}(t)\)は

\[ \mathbf{r}(t) = \mathbf{B}_0 \mathbf{r}(t) + \mathbf{e}(t) \]

を満たすので、VAR-LiNGAMの仮定より\(\mathbf{r}(t)\)は\(\mathbf{B}_0\)を隣接行列とするLiNGAMの仮定を満たします。したがってDirectLiNGAM等の方法で\(\mathbf{B}_0\)を推定できます。また、VARで推定された係数\(\mathbf{A}_\tau\)は

\[ \mathbf{A}_\tau=\left(\mathbf{I}-\mathbf{B}_0 \right)^{-1}\mathbf{B}_\tau \]

を満たすので、\(\mathbf{B}_\tau = \left(\mathbf{I}-\mathbf{B}_0 \right)\mathbf{A}_\tau\)として\(\mathbf{B}_\tau\)を復元できます。

以上がTwo-Stage Methodの概要です。纏めると、以下のようになります：

\(\mathbf{x}(t)\)に対してVARモデル\(\mathbf{x}(t) = \sum_{\tau=1}^p \mathbf{A}_\tau \mathbf{x}(t-\tau) + \mathbf{r}(t)\)の係数\(\mathbf{A}_\tau\)および残差\(\mathbf{r}(t)\)を推定する。
VARの残差\(\mathbf{r}(t)\)に対してDirectLiNGAMを用いて隣接行列\(\mathbf{B}_0\)を推定する。（DirectLiNGAMについてはLiNGAMによる因果探索（基本編）をご参照ください）
1.で求めた\(\mathbf{A}_\tau\)と2.で求めた\(\mathbf{B}_0\)から、ラグ\(\tau = 1, \dots, p\)の隣接行列\(\mathbf{B}_\tau = \left(\mathbf{I}-\mathbf{B}_0 \right)\mathbf{A}_\tau\)を計算する。
枝刈りを行う場合は、各変数\(x_i\)について\(x_i\)を目的変数に、以下の変数を説明変数としたadaptive lassoによる変数選択を行い、スパースな解を得る。すなわち、adaptive lassoで推定された係数の非零成分に対応する変数・ラグのみを\(x_i\)の真の原因変数とみなす：
- 同時刻間の因果関係のみに着目したとき、\(x_i\)に直接・間接問わず影響を与えている変数\(x_j(\text{lag 0})\)
- 過去からの影響に対応する変数全て、すなわち\(x_j(\text{lag }\tau)\hspace{10pt} (j=1, \dots, d, \ \tau=1, \dots, p)\)

なお、lingamライブラリではBICを用いて最適なラグ時間\(p\)を推定するアルゴリズムがデフォルトとなっています。すなわち、上記の1.の部分でラグ時間\(p=1, \dots, p_\text{max}\)それぞれについてVAR-LiNGAMの係数推定を行い、それらのうちBICが最小となったモデルを1.の最終的な推定結果とします。

必要なライブラリのインポート#

注意

本稿の実行例ではlingamライブラリv1.8.2を利用しており、解説もこのバージョンでの実装に基づいて行います。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns  # ヒートマップによる可視化用
import warnings  # 警告を無視する用

from lingam import VARLiNGAM  # VAR-LiNGAM本体
from sklearn.preprocessing import StandardScaler  # 前処理（標準化）用
from scipy import stats  # 正規性検定（Shapiro-Wilk検定）用

warnings.simplefilter("ignore")  # 警告を表示しないようにする1文
plt.rcParams["font.family"] = "MS Gothic"  # matplotlibで日本語フォントを使うための1文

データの準備#

ここでは、VAR-LiNGAMに従う人工データを用いて分析を行います。データの概要は以下の通りです：

サンプル数：1000
- 期間：1999-05-28から2002-02-20
- 間隔：1日
特徴量の個数：4（x0, x1, x2, x3）
最大ラグ時間：3

# VAR-LiNGAM人工データ生成
def VARLiNGAM_generate(adj: np.ndarray, noise: np.ndarray):
    d0, n_features, _ = adj.shape
    lags = d0 - 1
    n_samples = noise.shape[0]

    # Generate
    out = np.copy(noise)
    B = np.linalg.inv(np.eye(n_features) - adj[0])

    for i in range(lags):
        out[i] = B @ out[i]
    for i in range(lags, n_samples):
        for tau in range(1, lags + 1):
            out[i] += adj[tau] @ out[i - tau]
        out[i] = B @ out[i]

    return out

# VAR-LiNGAM用人工データの作成
n_samples = 1000
n_features = 4

# 真の隣接行列adj（同時刻の因果順序はx0 -> x1 -> x2 -> x3）
adj_varlingam = np.array(
    [
        # B0（同時刻間の直接効果。VAR-LiNGAMにおいてはこれが非巡回であると仮定する。）
        [[0, 0, 0, 0], [0.2, 0, 0, 0], [0, 0.2, 0, 0], [0, 0, 0.2, 0]],
        # B1（1時刻前からの直接効果）
        [[0.8, 0, 0, 0], [0, 0.8, 0, 0], [0, 0, 0.8, 0], [0, 0, 0, 0.8]],
        # B2（2時刻前からの直接効果）
        [[0, 0, 0, 0], [0, 0, 0, 0], [0.2, 0, 0, 0], [0, 0.2, 0, 0]],
        # B3（3時刻前からの直接効果）
        [[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0], [0.1, 0, 0, 0]],
    ]
)

# データX、データフレームdfの作成・保存
np.random.seed(0)
X_varlingam = VARLiNGAM_generate(
    adj=adj_varlingam,
    noise=np.random.uniform(low=-0.1, high=0.1, size=(n_samples, n_features)),
)
df = pd.DataFrame(
    data=X_varlingam,
    index=pd.date_range(start="1999-05-28", periods=n_samples, freq="D"),
    columns=[f"x{i}" for i in range(n_features)],
)

df.head(5)

	x0	x1	x2	x3
1999-05-28	0.009763	0.044990	0.029551	0.014887
1999-05-29	-0.015269	0.026125	-0.007258	0.076903
1999-05-30	0.092733	-0.004765	0.057392	0.017257
1999-05-31	0.087795	0.098866	-0.023160	-0.067199
1999-06-01	-0.025720	0.140473	0.083745	0.034512

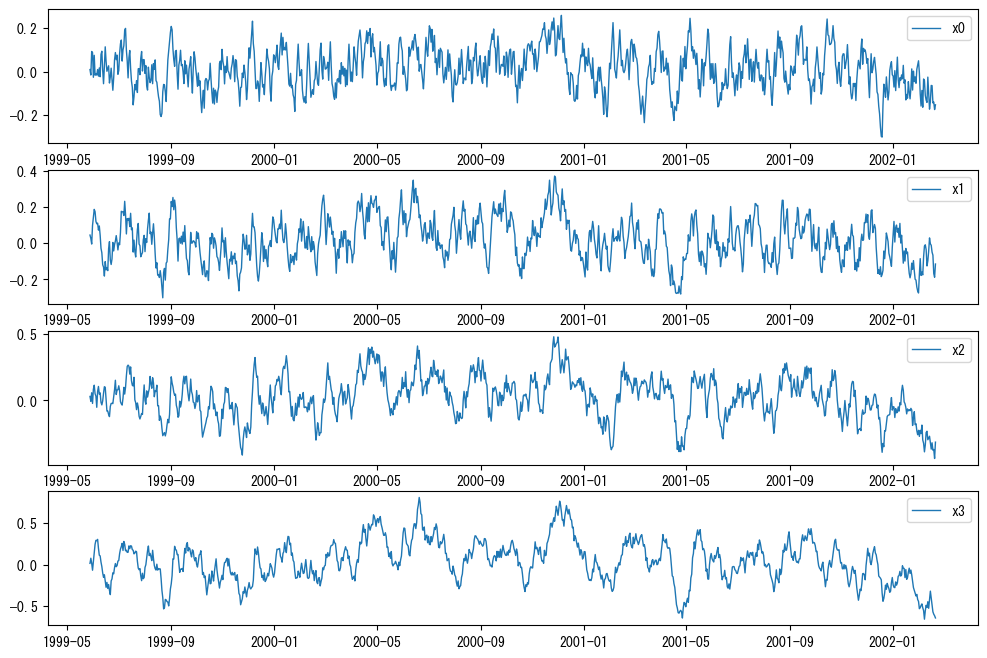
# 各成分の可視化
fig, axes = plt.subplots(n_features, 1, figsize=(12, 2 * n_features))

for col, ax in zip(df.columns, axes):
    ax.plot(df[col], label=col, linewidth=1)
    ax.legend()

../_images/85123c15bfe0669950d3f806ab0e0feebe90c91cb7432121910bcc8aaea2691b.png

前処理（標準化）#

VAR-LiNGAMを用いる際に前処理で標準化を行うべきか否かの判断は、基本的にLiNGAMによる因果探索（応用編）でで説明したものと同じになります。すなわち、lingamライブラリv1.8.2を使用するならば

ある変数の主原因を知りたい場合は、変数のスケールの違いを加味するため、標準化が必要
ある変数を1増やすごとに別のある変数がどれだけの割合で増えるか知りたい場合、標準化はしない

という風に使い分けます。

標準化が必要ならば、以下のようにして標準化を実行します：

sc = StandardScaler()
X_scaled = sc.fit_transform(df)  # Xを標準化したX_scaled(np.ndarray)を計算
df_scaled = pd.DataFrame(data=X_scaled, index=df.index, columns=df.columns)

# 先頭5行を表示
df_scaled.head(5)

	x0	x1	x2	x3
1999-05-28	-0.044031	0.226240	0.039550	-0.100707
1999-05-29	-0.316176	0.068286	-0.192507	0.147147
1999-05-30	0.858018	-0.190348	0.215075	-0.091233
1999-05-31	0.804337	0.677325	-0.292762	-0.428770
1999-06-01	-0.429803	1.025685	0.381214	-0.022272

本稿では標準化を行わずに分析を進める例を紹介します。標準化を行う場合は、以降でdfの代わりに上のdf_scaledを使います。

VAR-LiNGAMによる推定の実行#

まずは1回VAR-LiNGAMによる推定を行います。

lingamライブラリを使用する場合、VARLiNGAMインスタンス生成時のオプションで推定方法の詳細設定ができます。主なオプションは以下の通りです：

lags
- 最大ラグ時間です。最大で何ステップ前までの値が現在値に影響を与えていそうかを指定します。
- 下のcriterionでラグ時間の探索を行うよう指定した場合、ラグ時間の探索範囲が1~lagsとなります。
criterion
- ラグ時間の推定基準です。デフォルトはcriterion='bic'、すなわちラグ時間pを1~lagsの範囲内で探索し、BICが最小となるラグ時間を推定します。
- criterion=Noneとすると、ラグ時間の推定を行わずに上記のlagsを最大ラグ時間とします。
prune
- 推定の最後に枝刈りを実行するか否かを指定します。
- デフォルトではTrue、すなわち枝刈りを行います。

# 分析対象データの指定
data = df  # これは標準化なしの場合。標準化ありならdata=df_scaledとする。

# 推定器の生成と同時に、推定方法のオプションを指定。ここではcriterion(='bic')を基準に、ラグ時間を1~lags(=10)の範囲の中から推定する。
# criterion=Noneとすると、ラグ時間の探索を行わずに指定したlagsをそのまま最大ラグ時間として計算する。
vl = VARLiNGAM(lags=10, criterion="bic")

# 推定の実行
vl.fit(data)  # VAR-LiNGAMのラグ時間、係数の推定

<lingam.var_lingam.VARLiNGAM at 0x219141b3650>

Tip

VAR-LiNGAMにおいては、VARLiNGAM.fit(X)メソッドの実行時にLinAlgError: xx-th leading minor of the array is not positive definite.のエラーが発生することがあります。このエラーメッセージのleading minorとは、正定値性の確認に使われる首座小行列式のことです。VAR-LiNGAMの推定でラグ最適化を行う場合、BIC等の情報量基準を計算するためにノイズの共分散行列の行列式を計算するのですが、この時ノイズの共分散行列が退化しているとこのエラーが出ます。ノイズの共分散行列が退化する原因としては、多重共線性の存在が挙げられます。

解決策としては、多重共線性の原因となる変数を取り除くのがよいでしょう。

なお、もう一つの策としてVARLiNGAMのインスタンス生成時にcriterion=Noneのオプションを追加する、というものもあります。こうするとエラーの発生箇所となる情報量基準の計算自体を行わなくなるのでエラーを回避することはできますが、以下の理由からおすすめはできません：

多重共線性の存在という根本の原因を解消出来てはおらず、その結果推定された係数の推定誤差が拡大してしまう恐れがある
VAR-LiNGAMの特徴である「ラグを自動で決定できる」という強みを活かすことができていない

推定がうまく実行できた場合はadjacency_matrices_にアクセスして係数を確認し、\(1\)と比べて極端に絶対値の大きい係数が存在しないか確認するとよいでしょう。もし極端に値が大きい係数があれば、多重共線性が存在している恐れがあります。多重共線性については次元削減をご参照ください。

print(f"推定されたラグ時間: {vl._lags}")
print(f"係数:\n{vl.adjacency_matrices_}")

推定されたラグ時間: 1
係数:
[[[0.         0.         0.         0.        ]
  [0.21927711 0.         0.         0.        ]
  [0.         0.14620806 0.         0.        ]
  [0.         0.         0.20701212 0.        ]]

 [[0.78170003 0.         0.         0.        ]
  [0.         0.79347976 0.         0.        ]
  [0.         0.         0.81758946 0.        ]
  [0.         0.         0.         0.79330094]]]

VAR-LiNGAMの推定結果の信頼度評価#

本節ではLiNGAMによる因果探索（応用編）と同様に、前節で推定されたパラメータの信頼度を評価します。今回は以下の観点から評価します：

モデルの予測誤差
ノイズの独立性
ノイズの非正規性
ブートストラップ法

もし、上記の中で明らかにおかしい結果があればVAR-LiNGAMを使うのは適切ではない、ということになります。その場合は特徴量エンジニアリング等の前処理を工夫するか、あるいはVAR-LiNGAM以外の手法を使うことも検討すべきでしょう。

モデルの予測誤差確認#

まずは以下のコードでモデルの予測誤差を確認します：

# モデルの予測値と真値の比較（線形性の確認）
pred_data = data.iloc[vl._lags :] - vl.residuals_  # vl.residuals_は訓練データの残差

fig, axes = plt.subplots(n_features, 1, figsize=(12, 2 * n_features))

for col, ax in zip(df.columns, axes):
    ax.plot(data[col], label=f"{col}(true)", linewidth=1)
    ax.plot(pred_data[col], label=f"{col}(pred)", linewidth=1)
    ax.legend()

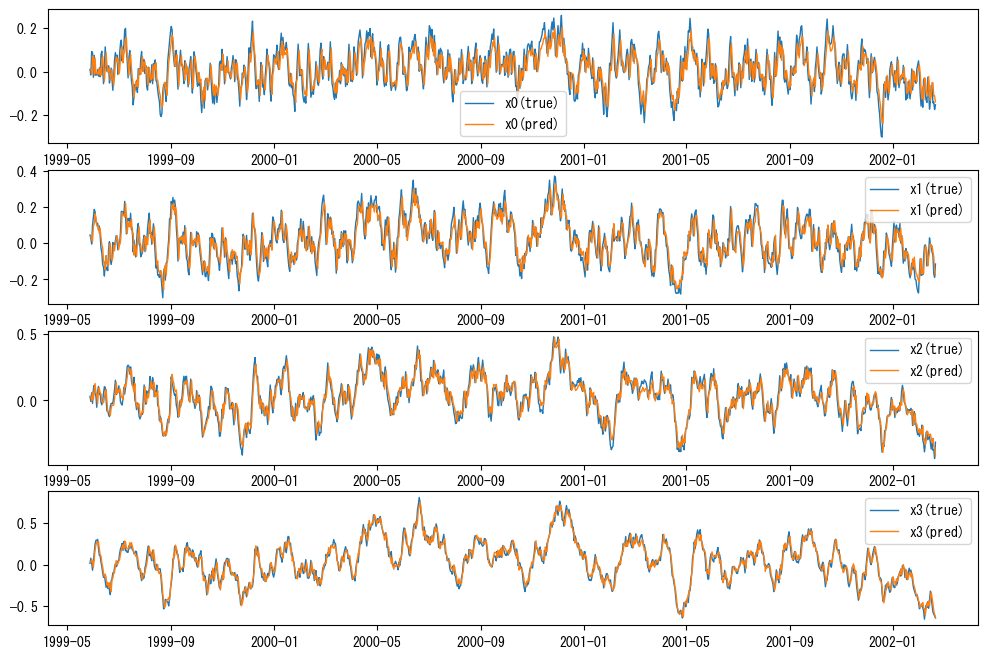
../_images/cded9e36b5594f0efcf2e767f953ecdbbd80af37bfca0961382a5149d4cd50d2.png

上のコードで描画したグラフは青が真値、橙がVAR-LiNGAMの予測値です。訓練期間はデータ全体なので、訓練期間に対する当てはまりの良さの確認になります。グラフを見たところ、今回のデータでは訓練期間の挙動をうまく説明できていそうです。

データの生成過程がVAR-LiNGAMの仮定（特に線形性）に従うならば、真値のトレンドをうまく予測できていることが期待されます。もし予測値が真値から大きく外れている場合はVAR-LiNGAMの仮定、特に線形性が満たされていない可能性が高いです。

ノイズの独立性検定#

次に、VAR-LiNGAMの仮定の一つであるノイズの独立性を確認してみます。以下のコードで2変数間のノイズ（残差）の独立性検定（HSIC test）のp値を計算します：

vl.get_error_independence_p_values()

array([[0.        , 0.43810916, 0.48178209, 0.45361346],
       [0.43810916, 0.        , 0.42811622, 0.47587719],
       [0.48178209, 0.42811622, 0.        , 0.17952051],
       [0.45361346, 0.47587719, 0.17952051, 0.        ]])

出力の第\((i,j)\)成分は、\(x_i, x_j\)の残差\(r_i, r_j\)間の独立性検定（HSIC test）におけるp値です。

HSIC testの帰無仮説は2つの確率変数が独立であることなので、これが棄却される（p値が有意水準\(\alpha=0.05\)を下回る）なら2つの確率変数が従属であると判断されます。すなわち、上の出力の非対角成分が全て有意水準\(\alpha=0.05\)以上であればノイズの独立性の仮定が破れていないことが期待できます。

なお、対角成分は同じ変数同士の独立性検定に対応するので、p値が0となっていても問題はありません。

HSIC testに用いられる独立性基準HSICについて詳しく知りたい場合はHilbert-Schmidt独立性基準（HSIC）もご参照ください。

2変数のノイズが従属となる現象は、例えばその2変数の未観測共通原因が存在する場合などに起こりえます。すなわち、その2変数の共通の原因変数が存在してかつその共通原因のデータを使用していない場合です。もし独立でない成分のペアがあった場合は、その2変数の未観測共通原因が存在していないか検討しましょう。もし未観測共通原因が存在しそうな場合はその未観測共通原因をデータに追加するか、あるいは未観測共通原因がある場合にも対応できる手法を利用しましょう。

注意

特徴量の数が増えると、仮に全てのノイズが独立であってもp値が有意水準を下回る変数のペアが生じる可能性は高まります。（cf. 検定の多重性）このため、非対角成分に有意水準を下回るものがあってもすぐ機械的にNGと判断せずに

p値がどの程度有意水準を下回るのか
そのペアの未観測共通原因がありそうか
独立性以外の他の結果（正規性検定・ブートストラップなど）

などの要素から総合的に判断するべきです。

また、今回は特徴量が4個と少なめでしたが、特徴量の数が多い場合は下のようにヒートマップで可視化するのもよいでしょう：

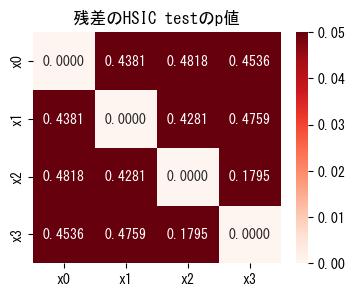
# おまけ：ヒートマップによる可視化例
fig, ax = plt.subplots(figsize=(4, 3))
ax.set_title("残差のHSIC testのp値")
sns.heatmap(
    data=vl.get_error_independence_p_values(),
    xticklabels=data.columns,
    yticklabels=data.columns,
    annot=True,
    fmt=".4f",
    vmin=0,
    vmax=0.05,
    cmap="Reds",
)

<Axes: title={'center': '残差のHSIC testのp値'}>

../_images/5dcbaa61b80d5e23a5460aee885cadb3e5ef063d60b2602a5590927acd24cf30.png

ノイズの非正規性#

次にVAR-LiNGAMの仮定の一つであるノイズの非正規性の仮定が満たされているか否かを、残差のShapiro-Wilk検定で確認します。Shapiro-Wilk検定は「確率変数が正規分布に従う」という帰無仮説に対する検定です。VAR-LiNGAMではノイズが正規分布に従わないという仮定を置いていたので、全ての残差について帰無仮説が棄却されるならばノイズの非正規性の仮定が破られてはいないだろうと期待されます。以下が実行例です：

alpha = 0.05  # 有意水準。p値がこれを下回ったものの背景を灰色にする。
fig, axes = plt.subplots(1, n_features, figsize=(4 * n_features, 4))

for i, (col, ax) in enumerate(zip(data.columns, axes.ravel())):
    Xi = vl.residuals_[:, i]
    p_value = stats.shapiro(Xi)[1]  # p-value of Shapiro-Wilk test
    if p_value < alpha:
        ax.set_facecolor("#d0d0d0")
    ax.set_title(f"{col} (p-value: {p_value:.4f})")
    ax.hist(Xi, bins="stone", color="C0", alpha=0.3, density=True)
    xlim = ax.get_xlim()
    x_pdf = np.linspace(xlim[0], xlim[1], 1000)
    ax.plot(
        x_pdf, stats.norm.pdf(x_pdf, loc=Xi.mean(), scale=Xi.std()), c="r"
    )  # draw p.d.f. of Gaussian distribution
    ax.set_xlim(*xlim)

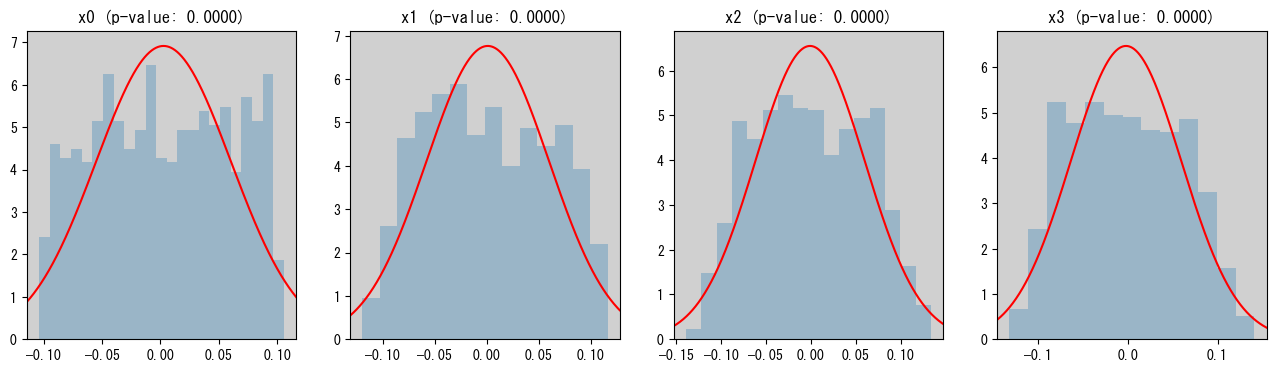
../_images/7a1b550fe29ce82f5c689eaecb142b78816c8ae6389a78d524d829b4431131c6.png

上の出力結果は、各変数の残差のヒストグラムと、正規分布の密度関数（赤線）を重ねて表示したものです。グラフタイトルにはShapiro-Wilk検定のp値が表示されており、これが有意水準（ここでは\(\alpha=0.05\)）を下回った、すなわち正規分布に従うという帰無仮説が棄却されたものは背景を灰色にしています。

全ての変数について帰無仮説が棄却された（i.e. 正規分布に従わないと判断された）ならば、VAR-LiNGAMにおけるノイズの非正規性の仮定が破られていないと思われます。逆に、帰無仮説が棄却されないなら、その変数周辺の因果関係には誤りが含まれる可能性が高く、注意が必要であると分かります。

今回のデータでは、全ての成分について帰無仮説が棄却されているので、ノイズがいずれも正規分布には従わない、すなわちVAR-LiNGAMにおけるノイズの非正規性の仮定が満たされていることが示唆されます。実際、このデータのノイズは一様分布に従っており、正規分布には従っていません。

なお先ほどの独立性検定と同様、この正規性検定でも特徴量の個数が増えると検定の多重性により「本当は正規分布に従うのに棄却される（あるいはその逆）」といったことが起こりやすくなる点に注意が必要です。

ブートストラップ法#

最後に、ブートストラップ法を用いて信頼度を確認します。

ブートストラップ法では、母集団の分布の近似分布から同じサイズの再標本（ブートストラップサンプル）を複数個サンプリングし、各再標本について推定量を計算します。これにより推定量の分布を近似的に得ることができるので、推定量の標準偏差や信頼区間の計算のほか、仮説検定を行う際などに活用されます。

通常、ブートストラップ法では母集団の分布をサンプルの経験分布で近似します。すなわち、サンプルのインデックスをランダムに復元抽出することで再標本を得るのですが、VAR-LiNGAMで取り扱うような時系列データに対しては同様の方法で再標本を得ると時系列性が壊れてしまいます。例えば、\(x(t+1)=x(t)+\varepsilon(t)\)（\(\varepsilon(t)\)は独立同分布に従うノイズ）というモデルに従う時系列\(x(t)\)があったとして、そこからインデックスを復元抽出して得た再標本\(y(t)\)にはもはや\(y(t+1)=y(t)+e(t)\)（\(e(t)\)は独立同分布に従うノイズ）のような関係式は成り立たないでしょう。

そのためlingamライブラリでは以下の手順でブートストラップサンプルを生成します：

全データでVARモデル\(\mathbf{x}(t) = \sum_{\tau=1}^p \mathbf{B}_\tau \mathbf{x}(t-\tau) + \mathbf{r}(t)\)を推定する
\(\mathbf{x}(t)\)から時系列性を除いたもの、すなわちVARの残差\(\mathbf{r}(t)\)から復元抽出したデータ\(\mathbf{r}'(t)\)を得る
その後、1.で推定したVARモデルに従って\(\mathbf{r}'(t)\)の上に時系列性を復元することで再標本\(\mathbf{x}'(t)\)を得る

例えばラグ\(p=2\)の場合、3.では

\[\begin{split} \begin{align*} \mathbf{x}'(0) &= \mathbf{r}'(0) \\ \mathbf{x}'(1) &= \mathbf{r}'(1) \\ \mathbf{x}'(2) &= \mathbf{B}_2 \mathbf{x}'(0) + \mathbf{B}_1 \mathbf{x}'(1) + \mathbf{r}'(2) \\ \mathbf{x}'(3) &= \mathbf{B}_2 \mathbf{x}'(1) + \mathbf{B}_1 \mathbf{x}'(2) + \mathbf{r}'(3) \end{align*} \end{split}\]

のようにして時系列性を復元した再標本\(\mathbf{x}'(0), \mathbf{x}'(1), \dots\)を生成します。

注意

1.で推定されたVARの係数が大きいと3.で時系列性を復元する際にブートストラップサンプルが発散する恐れがあります。ブートストラップの実行中、学習データにNaNが入っていないのにValueError: Input contains NaN.のエラーが出る場合はこのブートストラップサンプルが発散している可能性が高いです。このエラーの原因としては

多重共線性が存在する
非定常性が大きく、そもそもVAR部分の係数が大きい過程である

あたりが挙げられます。

前者であれば多重共線性の原因となる変数を取り除くことで解決が期待できます。ただしそれでも解決できない、あるいは後者の要因も絡む場合は解決は困難です。それでもなおVAR-LiNGAMを使うことにこだわるのであれば、例えば

VARの係数を定数倍して縮小させ、無理やり収束するようにする
ブロックブートストラッピングなどの別のブートストラップ方法を採用する

などの対応が考えられます。

では、以下でブートストラップ法の実行例を紹介します：

result = vl.bootstrap(
    X=data, n_sampling=100
)  # n_sampling(=100)回ブートストラップを行う
print(type(result))

<class 'lingam.var_lingam.VARBootstrapResult'>

上のコードで、VARBootstrapResult型のオブジェクトであるresultにブートストラップの結果が格納されました。resultに格納されている結果は以下の通りです：

result.adjacency_matrices_：\(i\)番目の要素が、\(i\)番目のブートストラップサンプルに対して推定された隣接行列\(\left[ \mathbf{B}_0 \cdots \mathbf{B}_p \right] \in \mathbb{R}^{d \times d(p+1)}\)となっているリスト。
result.total_effects_：第\((k, i, j)\)成分が\(k\)番目のブートストラップサンプルに対して推定された\(x_j \to x_i\)の総合効果となっている3次元配列

以下ではブートストラップの結果の可視化例をいくつか紹介します。

まずは因果グラフにおける辺の出現数の可視化を行ってみます。

# 辺の出現数ランキングの可視化
df_edge = pd.DataFrame(result.get_causal_direction_counts())
df_edge.head(5)  # 先頭5行（出現回数でソート済なので、つまり出現回数上位5個）の表示

	from	to	count
0	1	2	100
1	5	3	100
2	6	2	100
3	4	2	100
4	5	1	100

各行はそれぞれfrom → toのエッジがcount回出現したことを意味しており、countが多いものから順にソートされています。

fromやtoに現れる番号は変数のインデックスを表しており、データ中の変数が\(x_0, x_1, \dots, x_{d-1}\)であれば

インデックス\(0, 1, \dots, d-1\)が同時刻の\(x_0, x_1, \dots, x_{d-1}\)
インデックス\(d, d+1, \dots, 2d-1\)が\(1\)ステップ前の\(x_0, x_1, \dots, x_{d-1}\)
\(\cdots\)
インデックス\(pd, pd+1, \dots, (p+1)d-1\)が\(p\)ステップ前の\(x_0, x_1, \dots, x_{d-1}\)

にそれぞれ対応します。この対応関係は、以降の可視化例でも共通です。

インデックスと変数の対応を辞書で表すと下のようになります：

var_dict = {
    i: f"{data.columns[i % n_features]}(lag{i // n_features})"
    for i in range(n_features * (vl._lags + 1))
}
print(var_dict)

{0: 'x0(lag0)', 1: 'x1(lag0)', 2: 'x2(lag0)', 3: 'x3(lag0)', 4: 'x0(lag1)', 5: 'x1(lag1)', 6: 'x2(lag1)', 7: 'x3(lag1)'}

この辞書を用いて下のようにエッジのカウントを書き直すと、以下のようになります：

df_edge_name = df_edge.copy()
df_edge_name[["from", "to"]] = df_edge_name[["from", "to"]].map(lambda i: var_dict[i])
df_edge_name.head(5)  # 先頭5行（出現回数でソート済なので、つまり出現回数上位5個）の表示

	from	to	count
0	x1(lag0)	x2(lag0)	100
1	x1(lag1)	x3(lag0)	100
2	x2(lag1)	x2(lag0)	100
3	x0(lag1)	x2(lag0)	100
4	x1(lag1)	x1(lag0)	100

注意

辺に限らず、次で紹介する総合効果の可視化でもそうですが、lingamライブラリの実装ではラグ0の変数に対する辺や総合効果しか表示しないようになっています。これはどういうことかというと、VAR-LiNGAMでは例えば「1ステップ前の\(x_1\)から現在の\(x_0\)への辺」が存在するときは「2ステップ前の\(x_1\)から1ステップ前の\(x_0\)への辺」も存在します。ですが前者の存在が分かれば後者が存在することも分かり逆もまた然りであるため、ラグ0の変数に対する辺の存在だけ表示すれば十分、という背景です。

ということで、可視化の際に例えば「1ステップ前の\(x_1\)から現在の\(x_0\)への辺」が存在すると分かった場合は「\(\tau+1\)ステップ前の\(x_1\)から\(\tau\)ステップ前の\(x_0\)への辺」も存在している、ということは頭の片隅に入れておきましょう。

次に、総合効果の可視化を行ってみます。

# 総合効果の可視化
df_total_effect = pd.DataFrame(result.get_total_causal_effects())
df_total_effect.head(
    5
)  # 先頭5行（出現確率でソート済なので、つまり出現確率上位5個）の表示

	from	to	effect	probability
0	1	2	0.248055	1.0
1	5	3	0.199761	1.0
2	6	2	0.816827	1.0
3	5	2	0.111743	1.0
4	4	2	0.157894	1.0

上の出力結果の各行は「fromからtoに対して大きさが非零の総合効果が発生した割合がprobabilityであり、それら非零の総合効果の中央値がeffectであった」ことを意味しており、probabilityが高いものから順にソートされています。

fromやtoに現れる番号は辺の出現回数の可視化の時と同様、変数のインデックスを表しています。インデックスと変数名・ラグの対応をもとに上の出力結果を書き直すと下のようになります：

# 総合効果の整理
df_total_effect_detail = pd.DataFrame(result.get_total_causal_effects())
df_total_effect_detail[["from_var", "to_var"]] = df_total_effect_detail[
    ["from", "to"]
].map(lambda i: data.columns[i % len(data.columns)])
df_total_effect_detail["from_lag"] = df_total_effect_detail["from"].map(
    lambda i: f"lag{i // len(data.columns)}"
)

df_total_effect_detail.head(
    5
)  # 先頭5行（出現確率でソート済なので、つまり出現確率上位5個）の表示

	from	to	effect	probability	from_var	to_var	from_lag
0	1	2	0.248055	1.0	x1	x2	lag0
1	5	3	0.199761	1.0	x1	x3	lag1
2	6	2	0.816827	1.0	x2	x2	lag1
3	5	2	0.111743	1.0	x1	x2	lag1
4	4	2	0.157894	1.0	x0	x2	lag1

上の出力結果は、fromやtoカラムのインデックスを対応する変数名・ラグに変換したfrom_var、to_var、from_lagカラムを追加したものです。

この結果をさらにto_varカラムで条件付けすれば、ある変数に対する総合効果を可視化できます。

# ある変数に対する総合効果の可視化
to_var = "x3"  # 注目する目的変数
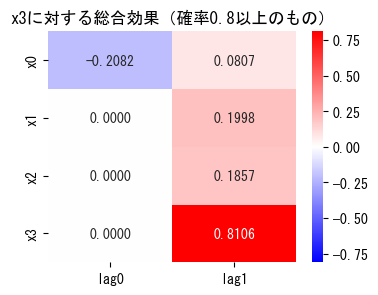
df_total_effect_detail[df_total_effect_detail["to_var"] == to_var]

	from	to	effect	probability	from_var	to_var	from_lag
1	5	3	0.199761	1.00	x1	x3	lag1
5	6	3	0.185712	1.00	x2	x3	lag1
7	7	3	0.810567	1.00	x3	x3	lag1
10	4	3	0.080671	0.99	x0	x3	lag1
11	0	3	-0.208214	0.94	x0	x3	lag0
13	1	3	-0.072928	0.74	x1	x3	lag0
14	2	3	0.150247	0.57	x2	x3	lag0

ヒートマップにすると下のようになります：

# ある変数に対する総合効果の可視化
to_var = "x3"  # 注目する目的変数
min_prob = 0.8  # 出現確率がこれ以上の総合効果のみを可視化する

df_causes = pd.DataFrame(
    data=0, index=data.columns, columns=[f"lag{l}" for l in range(vl._lags + 1)]
)

for _, row in df_total_effect_detail[
    df_total_effect_detail["to_var"] == to_var
].iterrows():
    if row["probability"] >= min_prob:
        df_causes.loc[row["from_var"], row["from_lag"]] = row["effect"]

# df_causesをヒートマップで可視化
fig, ax = plt.subplots(figsize=(4, 3))
max_abs = np.max(np.abs(df_causes.values))
ax.set_title(f"{to_var}に対する総合効果（確率{min_prob}以上のもの）")
sns.heatmap(
    data=df_causes, annot=True, vmin=-max_abs, vmax=max_abs, fmt=".4f", cmap="bwr"
)
fig.show()

../_images/267f14ed8e453a552966599267db4b19fd0029d6441a6e8448c922d9859ae421.png

総合効果の発生している変数の組について、総合効果を発生させている経路のリストは下のようにして可視化することが可能です：

# from_index -> to_indexの総合効果の発生経路の可視化
df_path = pd.DataFrame(result.get_paths(from_index=7, to_index=3))
df_path["path"] = df_path["path"].map(lambda l: [var_dict[i] for i in l])
df_path.head(5)  # 先頭5行（出現確率でソート済なので、つまり出現確率上位5個）の表示

	path	effect	probability
0	[x3(lag1), x3(lag0)]	0.810382	1.00
1	[x3(lag1), x2(lag0), x3(lag0)]	-0.004622	0.25
2	[x3(lag1), x2(lag0), x0(lag0), x3(lag0)]	0.005673	0.06
3	[x3(lag1), x2(lag1), x3(lag0)]	-0.009774	0.05
4	[x3(lag1), x1(lag0), x3(lag0)]	0.001093	0.02

上の出力結果はfrom=index=7からto_index=3、すなわち\(x_3\)（\(1\)ステップ前）から\(x_3\)への総合効果の内訳を表しており、各行は「pathの経路を通じて大きさが非零の総合効果が発生した確率がprobabilityであり、それら非零の総合効果の中央値がeffectであった」ことを意味します。

注釈

ここではget_causal_direction_counts、get_total_causal_effectsなどを利用したブートストラップ結果の可視化を紹介しました。ここでは簡単な使い方の紹介にとどめましたが、lingamライブラリではほかにも

辺の出現確率を重みとする因果グラフの隣接行列を計算するget_probabilities
辺の出現数のカウント時に重みの正負で別の辺とみなすオプションsplit_by_causal_effect_sign
絶対値が閾値以下の辺や総合効果を無視するオプションmin_causal_effect

などが利用できます。より詳細な使い方についてはBootstrapResultのAPI Referenceをご参照ください。

小括#

以上がVAR-LiNGAMの解説およびVAR-LiNGAMを用いた分析例となります。VAR-LiNGAMに限らず、モデル・手法の仮定が満たされない状態で推定を行うと誤った結果が出る確率が高まり、誤った結論を出してしまうことに繋がります。そのような事態を回避するためにも、VAR-LiNGAMを使用する際は本稿の内容を参考に仮定の確認やブートストラップによる信頼度評価を併せて行いながら、課題の解決に役立てて頂けると幸いです。